文章目录
习题2-1
11 证明
(1)若 f ( x ) f(x) f(x)为可导的奇函数,则 f ′ ( x ) f^{'}(x) f′(x)为偶函数;(2)若 f ( x ) f(x) f(x)为可导的偶函数,则 f ′ ( x ) f^{'}(x) f′(x)为奇函数;(3)若f(x)为偶函数,且 f ′ ( 0 ) f^{'}(0) f′(0)存在,则 f ′ ( 0 ) = 0 f^{'}(0)=0 f′(0)=0
证明: f ( x ) 可导则 f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f ′ ( − x ) = lim h → 0 f ( − x − h ) − f ( − x ) − h ( 1 )若 f ( x ) 为奇函数,则 f ( x ) = − f ( − x ) f ′ ( − x ) = lim h → 0 f ( − x − h ) − f ( − x ) − h = lim h → 0 f ( x + h ) − f ( x ) h = f ′ ( x ) 即 f ′ ( x ) 为偶函数。 ( 2 )若 f ( x ) 为偶函数,则 f ( x ) = f ( − x ) f ′ ( − x ) = lim h → 0 f ( x + h ) − f ( x ) − h = − lim h → 0 f ( x + h ) − f ( x ) h = − f ′ ( x ) 即 f ′ ( x ) 为奇函数函数。 ( 3 ) 由( 2 )知 f ′ ( 0 ) = − f ′ ( 0 ) ∴ f ′ ( 0 ) = 0 证明:\\ f(x)可导则\\ f^{'}(x)=\lim_{h\to0}{\frac{f(x+h)-f(x)}{h}} \\ f^{'}(-x)=\lim_{h\to0}{\frac{f(-x-h)-f(-x)}{-h}}\\ (1)若f(x)为奇函数,则f(x)=-f(-x)\\ f^{'}(-x)=\lim_{h\to0}{\frac{f(-x-h)-f(-x)}{-h}}\\ =\lim_{h\to0}{\frac{f(x+h)-f(x)}{h}}=f^{'}(x)\\ 即f^{'}(x)为偶函数。\\ (2)若f(x)为偶函数,则f(x)=f(-x)\\ f^{'}(-x)=\lim_{h\to0}{\frac{f(x+h)-f(x)}{-h}}\\ =-\lim_{h\to0}{\frac{f(x+h)-f(x)}{h}}=-f^{'}(x)\\ 即f^{'}(x)为奇函数函数。\\ (3)由(2)知f^{'}(0)=-f^{'}(0)\\ \therefore f^{'}(0)=0 证明:f(x)可导则f′(x)=h→0limhf(x+h)−f(x)f′(−x)=h→0lim−hf(−x−h)−f(−x)(1)若f(x)为奇函数,则f(x)=−f(−x)f′(−x)=h→0lim−hf(−x−h)−f(−x)=h→0limhf(x+h)−f(x)=f′(x)即f′(x)为偶函数。(2)若f(x)为偶函数,则f(x)=f(−x)f′(−x)=h→0lim−hf(x+h)−f(x)=−h→0limhf(x+h)−f(x)=−f′(x)即f′(x)为奇函数函数。(3)由(2)知f′(0)=−f′(0)∴f′(0)=0
20 证明:双曲线 x y = a 2 xy=a^2 xy=a2上任一点处的切线与两坐标轴构成的三角形的面积都等于 2 a 2 2a^2 2a2
证明: 当 a ≠ 0 时, y = a 2 x 切线斜率 k = f ′ ( x ) = − a 2 x 2 任取 f ( x ) 上一点 ( x 0 , a 2 x 0 ) , 则切线方程为 y − a 2 x 0 = − a 2 x 0 2 ( x − x 0 ) 切线与 y 轴相交, x = 0 , y = 2 a 2 x 0 切线与 x 轴相交, y = 0 , x = 2 x 0 ∴ 切线与坐标轴相交三角形面积 : s = 1 2 x ⋅ y = 2 a 2 当 a = 0 时,也成立 证明:\\ 当a\not=0时,y=\frac{a^2}{x}\\ 切线斜率k=f^{'}(x)=-\frac{a^2}{x^2}\\ 任取f(x)上一点(x_0,\frac{a^2}{x_0}),则切线方程为 y-\frac{a^2}{x_0}=-\frac{a^2}{x_0^2}(x-x_0)\\ 切线与y轴相交,x=0,y=2\frac{a^2}{x_0}\\ 切线与x轴相交,y=0,x=2x_0\\ \therefore 切线与坐标轴相交三角形面积:s=\frac{1}{2}x\cdot y=2a^2\\ 当a=0时,也成立 证明:当a=0时,y=xa2切线斜率k=f′(x)=−x2a2任取f(x)上一点(x0,x0a2),则切线方程为y−x0a2=−x02a2(x−x0)切线与y轴相交,x=0,y=2x0a2切线与x轴相交,y=0,x=2x0∴切线与坐标轴相交三角形面积:s=21x⋅y=2a2当a=0时,也成立
a ≠ 0 a\not=0 a=0时双曲线 x y = a 2 xy=a^2 xy=a2切线与坐标轴相交图形如下所示: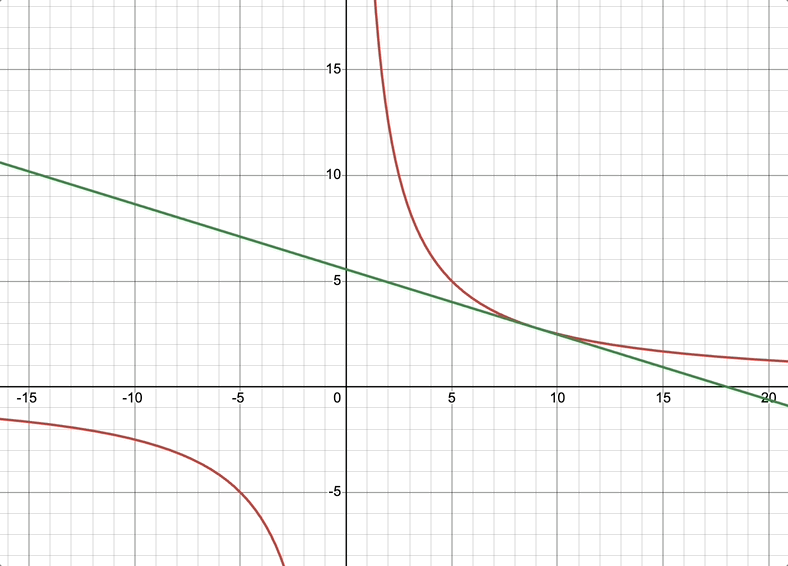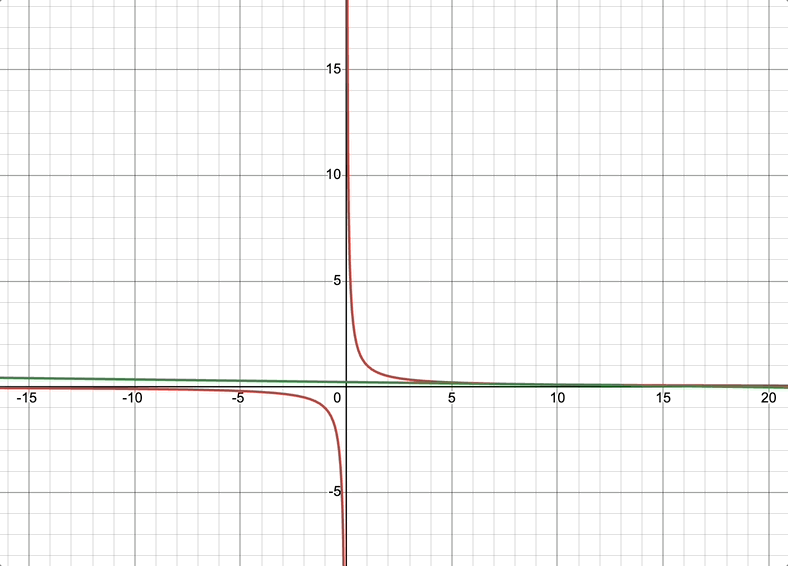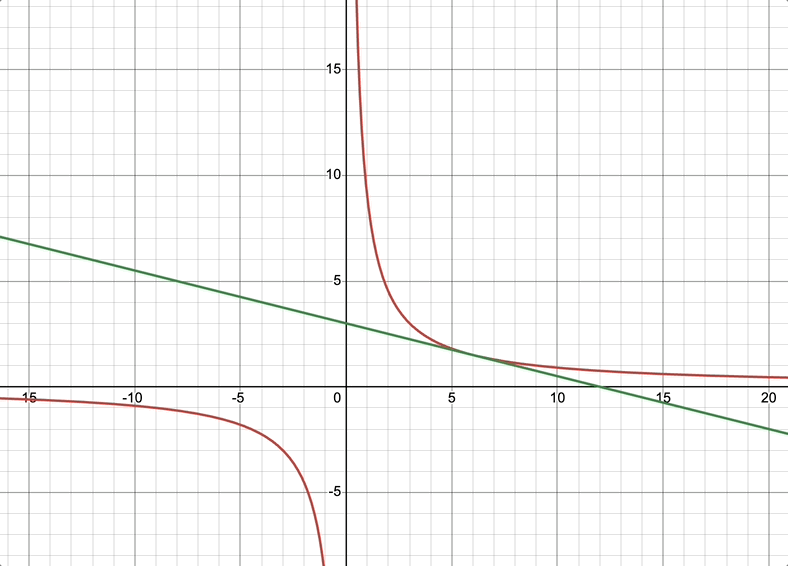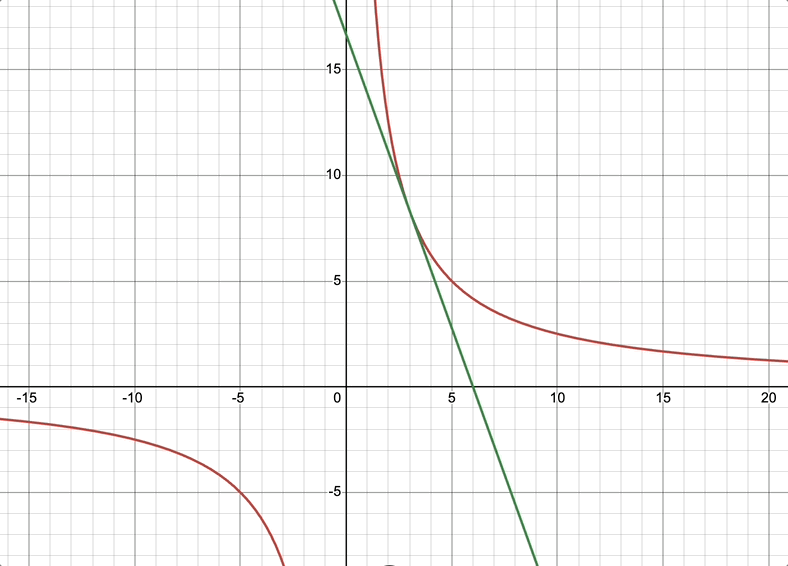
习题2-4
例10 一气球从离开观察员500m处离地面铅直上升,当气球高度为500m时,其速率为140m/min。求此时观察员视线的仰角增加的速率是多少?
图示:
解: 观察员身高这里我们忽略不计 设气球上升上升 t ( m i n ) 后 , 其高度为 h ,观察员视线的仰角为 α , 则 tan α = h 500 其中 α 和 h 都与 t 存在可导的函数关系,上式两端对 t 求导,得 sec 2 α d α d t = 1 500 d h d t 由已知条件知,存在 t 0 时刻,使得 h ∣ t = t 0 = 500 m , d h d t ∣ t = t 0 = 140 m / m i n , tan α ∣ t = t 0 = 1 , sec 2 α = 2 , 带入上式得 2 ⋅ d α d t t = t 0 = 1 500 ⋅ 140 d α d t t = t 0 = 0.14 r a d / m i n 即此刻观察员视线仰角增加的速率为 0.14 r a d / m i n 解:\\ 观察员身高这里我们忽略不计\\ 设气球上升上升t(min)后,其高度为h,观察员视线的仰角为\alpha,则\\ \tan\alpha = \frac{h}{500}\\ 其中\alpha和h都与t存在可导的函数关系,上式两端对t求导,得\\ \sec^2\alpha\frac{d\alpha}{dt}=\frac{1}{500}\frac{dh}{dt}\\ 由已知条件知,存在t_0时刻,使得\\ h|{t=t_0}=500m,\frac{dh}{dt}|{t=t_0}=140m/min,\tan\alpha|{t=t_0}=1,\sec^2\alpha=2,带入上式得\\ 2\cdot\frac{d\alpha}{dt}{t=t_0}=\frac{1}{500}\cdot 140\\ \frac{d\alpha}{dt}_{t=t_0}=0.14rad/min\\ 即此刻观察员视线仰角增加的速率为0.14rad/min 解:观察员身高这里我们忽略不计设气球上升上升t(min)后,其高度为h,观察员视线的仰角为α,则tanα=500h其中α和h都与t存在可导的函数关系,上式两端对t求导,得sec2αdtdα=5001dtdh由已知条件知,存在t0时刻,使得h∣t=t0=500m,dtdh∣t=t0=140m/min,tanα∣t=t0=1,sec2α=2,带入上式得2⋅dtdαt=t0=5001⋅140dtdαt=t0=0.14rad/min即此刻观察员视线仰角增加的速率为0.14rad/min
例10 落在平静水面上的石头,产生同心波纹,若最外一圈半径的增大速率为 6 m / s 6\quad m/s 6m/s,问在2s末扰动水面面积增大的速率为多少?
解 : 设在时间 t ( s ) 后,最外一圈圆面积为 s ,半径 r 则 s = π r 2 = π ( 6 t ) 2 = 36 π t 2 s ′ ( t ) = 72 π t s ′ ( t ) ∣ t = 2 = 144 π m 2 / s 即在 2 s 末扰动水面面积增大的速率为 144 π m 2 / s 解:\\ 设在时间t(s)后,最外一圈圆面积为s,半径r则\\ s=\pi r^2=\pi(6t)^2=36\pi t^2\\ s^{'}(t)=72\pi t\\ s^{'}(t)|_{t=2}=144\pi\quad m^2/s\\ 即在2s末扰动水面面积增大的速率为144\pi\quad m^2/s 解:设在时间t(s)后,最外一圈圆面积为s,半径r则s=πr2=π(6t)2=36πt2s′(t)=72πts′(t)∣t=2=144πm2/s即在2s末扰动水面面积增大的速率为144πm2/s
11 注水入深8m,上顶直径8m的正圆锥形容器中,其速率为 4 m 3 / m i n 4 m^3/min 4m3/min。当水深为5m时,其表面上升的速率为多少?
如下图所示 :
解: 设在时间 t 时刻,水深 h ( t ) ,谁容积 v ( t ) , 水面半径 r ( t ) ,则 h ( t ) 8 = r ( t ) 4 ⇒ r ( t ) = 1 2 h ( t ) v ( t ) = 1 3 π ⋅ r 2 ( t ) ⋅ h ( t ) = 1 3 π ⋅ 1 4 h 3 ( t ) 等式两边对 t 求导 d v d t = 1 4 π ⋅ h 2 ( t ) ⋅ d h d t 由题知,在 t 0 时刻 d v d t ∣ t = t 0 = 4 , h 2 ( t ) ∣ t = t 0 = 25 , 导入上式得 d h d t ∣ t = t 0 = 16 25 π m / m i n 即在 t 0 时刻其表面上升速率为 16 25 π m / m i n 解:\\ 设在时间t时刻,水深h(t),谁容积v(t),水面半径r(t),则\\ \frac{h(t)}{8}=\frac{r(t)}{4}\Rightarrow r(t)=\frac{1}{2}h(t)\\ v(t)=\frac{1}{3}\pi\cdot r^2(t)\cdot h(t)=\frac{1}{3}\pi\cdot \frac{1}{4}h^3(t)\\ 等式两边对t求导\\ \frac{dv}{dt}=\frac{1}{4}\pi\cdot h^2(t)\cdot \frac{dh}{dt}\\ 由题知,在t_0时刻\\ \frac{dv}{dt}|{t=t_0}=4,\quad h^2(t)|{t=t_0}=25,导入上式得 \\ \frac{dh}{dt}|_{t=t_0}=\frac{16}{25\pi} m/min\\ 即在t_0时刻其表面上升速率为\frac{16}{25\pi} \quad m/min 解:设在时间t时刻,水深h(t),谁容积v(t),水面半径r(t),则8h(t)=4r(t)⇒r(t)=21h(t)v(t)=31π⋅r2(t)⋅h(t)=31π⋅41h3(t)等式两边对t求导dtdv=41π⋅h2(t)⋅dtdh由题知,在t0时刻dtdv∣t=t0=4,h2(t)∣t=t0=25,导入上式得dtdh∣t=t0=25π16m/min即在t0时刻其表面上升速率为25π16m/min
习题2-5
11 计算球体体积时,要求精确度在 2 % 2\% 2%以内,问这时测试直径D的相对误差不能超过多少?
解 : v = 4 3 π r 3 = 1 6 π D 3 v ′ = 1 2 π D 2 Δ D ∣ d v v ∣ < 0.02 ⇒ ∣ 3 Δ D D ∣ < 0.02 ∣ Δ D D ∣ < 1 150 ≈ 0.667 % 因此测试直径 D 不能超过 0.667 % 解:\\ v=\frac{4}{3}\pi r^3=\frac{1}{6}\pi D^3\\ v^{'}=\frac{1}{2}\pi D^2\Delta D\\ |\frac{dv}{v}|\lt 0.02\Rightarrow |\frac{3\Delta D}{D}|\lt 0.02\\ |\frac{\Delta D}{D}|\lt \frac{1}{150}\approx 0.667\%\\ 因此测试直径D不能超过0.667\% 解:v=34πr3=61πD3v′=21πD2ΔD∣vdv∣<0.02⇒∣D3ΔD∣<0.02∣DΔD∣<1501≈0.667%因此测试直径D不能超过0.667%
结语
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
1\]同济大学数学系.高等数学 第七版 上册\[M\].北京:高等教育出版社,2014.7.p73-124. \[2\][《高等数学》课后习题,兼容同济七版和八版](https://www.bilibili.com/video/BV1wH4y1F7R6)\[CP/OL\].2024-09-01.p21-35.