力扣HOT100——102.二叉树层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

复制代码

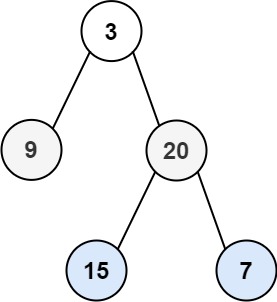
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:


    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return {};
        vector<vector<int>> ans;
        vector<TreeNode *> cur={root};
        while(cur.size())
        {
            vector<int> vals;
            vector<TreeNode *> nxt;
            for(auto x:cur)
            {
                vals.push_back(x->val);
                if(x->left) nxt.push_back(x->left);
                if(x->right) nxt.push_back(x->right);

            }
            ans.push_back(vals);
            cur=nxt;
        }
        return ans;

    }
};

思路：

先判断二叉树根节点是否为空，为空则直接返回空结果；接着初始化存储结果的二维向量 `ans` 和存储当前层节点的向量 `cur`（初始含根节点），然后通过 `while` 循环不断迭代，每次循环中先定义存储当前层节点值的 `vals` 和存储下一层节点的 `nxt`，再遍历当前层节点，将其值存入 `vals`，并把左右子节点（若存在）存入 `nxt`，循环结束后将 `vals` 加入 `ans`，最后更新 `cur` 为 `nxt`，如此反复直至遍历完二叉树所有层，最终返回 `ans` 得到二叉树的层序遍历结果。

时间复杂度为 O(n)，空间复杂度也为 O(n)，n是二叉树的节点数