随机事件及其概率
加法公式

推三个的时候ABC,夹逼准则

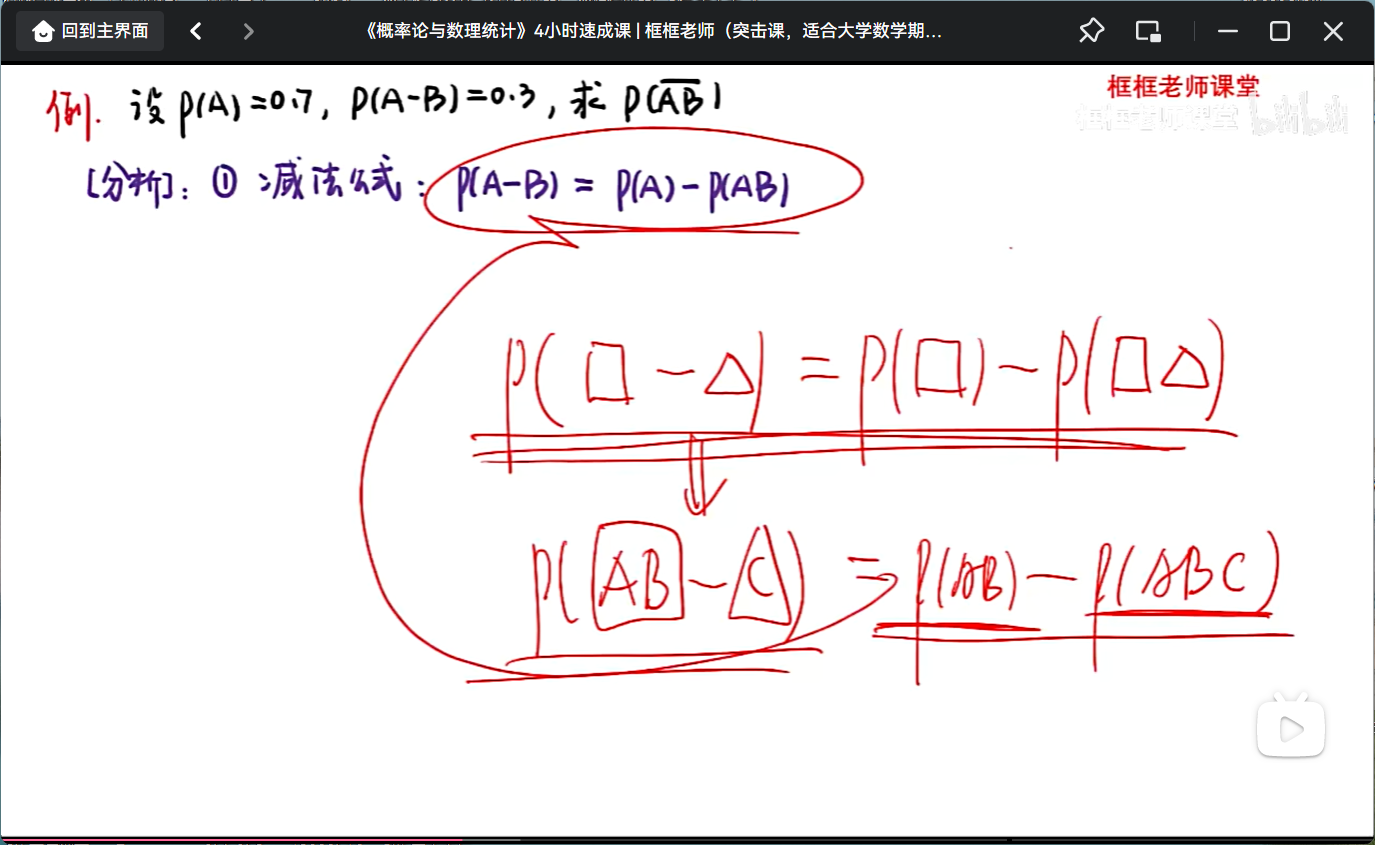
减法准则

除法公式


相互独立定义


两种分析 两个解法

古典概型求概率(排列组合)
分步相乘、分类相加

全概率公式和贝叶斯公式
两阶段问题
第一个小概率*A在小概率的概率。。。累计

分子*反过来/全概率

求谁把谁设为A

例题

看到:已知、条件下 用条件概率
确定A的条件下,求某一个小概率,用贝叶斯
求A 用全概率公式

伯努利概型

一维随机变量及其分布
离散型求分布律(表格)

关乎顺序用A

常见离散分布 求概率
如二项分布

连续性随机变量(RV)相关计算
分布函数F(x)求导,得到密度f(x)
已知密度f(x),求区间概率P,定积分(导回去)。或者用分布函数区间前后减去

概率密度为相同值的情况下,可以合并条件为其他
例题

已知f求常数、F
求K------规范性
不定积分(导回去),别忘记常数


不定积分!!!别忘记常数了

三个任意常数的情况
密度f有其他的区域条件
------在分段点处连续------左极限=右极限

二、一维随机变量
U均匀分布
求子区间的概率密度,用长度之比即可

N正态分布_标准化
标准化,使得呈现y轴对称,括号右边,越小越尖
N(0,1)标准正态分布,和y轴对称

例题
求概率:1.画图即得到 2.利用公式法,转化为标准正态分布,因为要求P(x<0),标准化,使得为 (-2),题目中2-4,标准化后为2,0,根据正反相加为1,即得相反数
(-2),题目中2-4,标准化后为2,0,根据正反相加为1,即得相反数

泊松分布
二项式和泊松定理可以互相转化

离散型 函数分布
分布律------先求取值,再求概率

连续型函数分布(不懂)!!
y的函数两个分段点,分三段来考虑;1个就分2段
分布函数定义:X随机变量<x自变量
求出密度函数---代入所求函数,按照分段点,把x划出来,定积分,求得区域分布函数

注意 分母不为0

二维随机变量及其分布
二维离散型 分布
联合分布律是表格,边缘分布律行行列列相加


边缘分布律
别把X Y搞混了


条件分布律
不可以直接在表格中摘出来,用符合的概率/在那个条件下的整体的概率(例如在Y=1的条件下,就要把Y=1的概率全部加起来)


独立与否
看每行成不成比例

大题:联合概率 不等于 边缘概率的乘积------P(x,y)不等于P(x)*P(y)

二维 连续型!!必考最后一道
解题方法

求未知参数
已知f(x,y),反求参数,用规范性------区域内的不定积分=1
注意函数区域D画对,这样积分上下限才是对的
二重积分:一个积分积完,结果直接代入到下一重积分内,化简即得
根据密度函数的分布,画出区域--得到积分上下限

求区域密度
在题目的基础上的新的小区域
区域要写成该题要求和题目的区域的交集,双重积分,就把f(x,y)带入再化开区域解
y的上下限,穿y------从下至上


求边缘密度函数
给对方定积分,就会把对方消掉
求概率值不能代0,但是函数可以为0,所以别漏掉
求x的边缘密度就竖着,y的就横着,
积分上下限:y从下到上。x从左到右
边缘密度的每一个区域都要重新求


条件密度(有比/)
=联合密度/边缘密度


独立与否
边缘密度相乘 ==联合密度

两个离散型 函数 分布律

两个连续函数 求密度函数(跳过一下)
随机变量的数字特征
数学期望、方差
U均匀分布、N正态分布、P泊松分布
D方差
不独立的情况下,拆开还要加上2倍的协方差
D=平方的期望-期望的平方

常数提出来要变成平方倍的
例题

离散型 协方差、相关系数
协方差=乘积的期望-期望的乘积
先求和再求协方差=先求协方差再求和
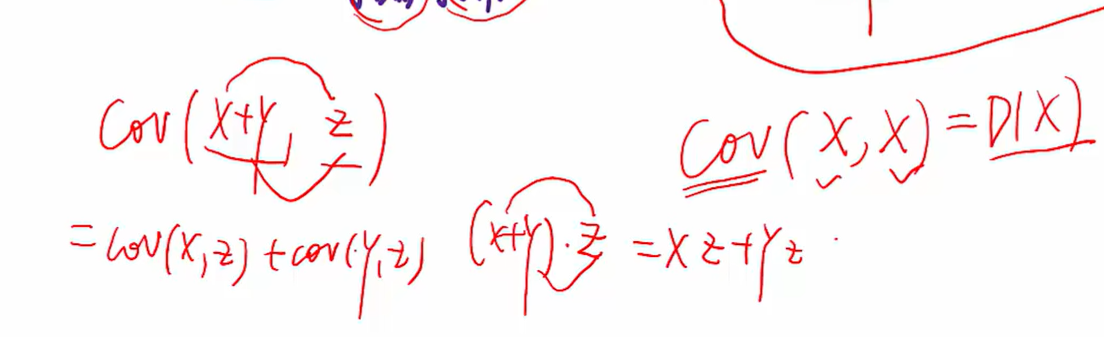
例题

连续型的 协方差、相关系数
独立可以推不相关,不相关不能推独立
先取值 再积分
E(XY)=取值(xy)*密度函数再二重积分
积分上下限 由无穷变为D区域


例题

若要求 平方的期望,把Y平方代入到期望的表达式进行积分即可
不相关是指没有线性关系
切比雪夫不等式求概率(跳过了)
假设检验
正态分布下均值
小概率对应的区间------拒绝域
s是样本标准差,没给就按下面公式算(比起标准差------把1/n-1放在了根号里面)


拒绝域------考试会给表,查数值

注意U检验时,是密度,而不是密度的平方
算出统计量,看在拒绝域嘛------在就不正常

正态下方差
s样本标准差



