【机器学习基础】机器学习入门核心算法：线性回归（Linear Regression）

机器学习入门核心算法：线性回归（Linear Regression）

- [1. 算法逻辑](#1. 算法逻辑)
- [2. 算法原理与数学推导](#2. 算法原理与数学推导)
- [3. 评估指标](#3. 评估指标)
- [4. 应用案例](#4. 应用案例)
- [5. 面试题](#5. 面试题)
- [6. 扩展分析](#6. 扩展分析)
- 总结

1. 算法逻辑

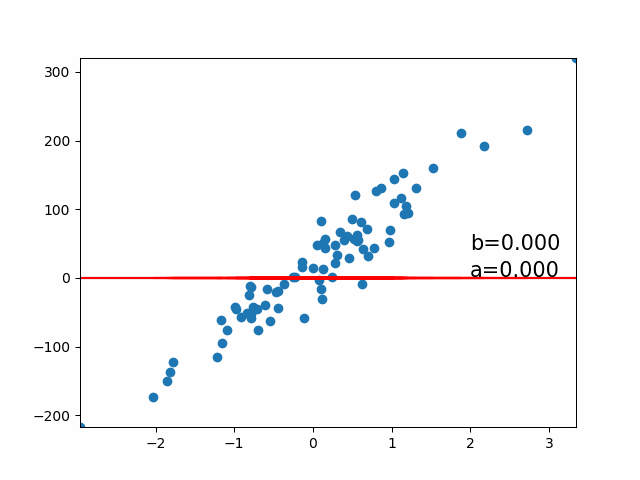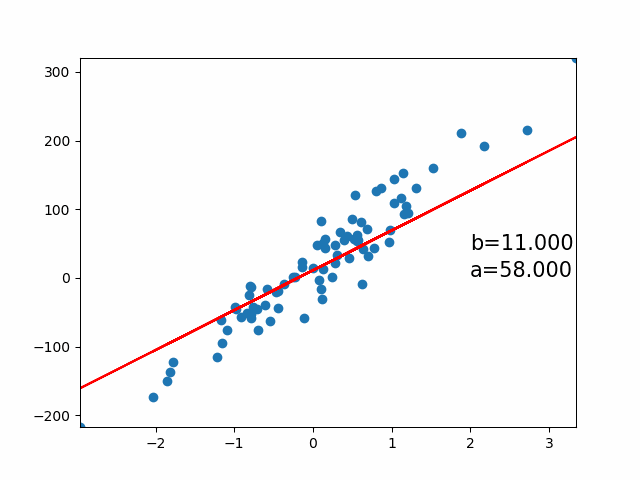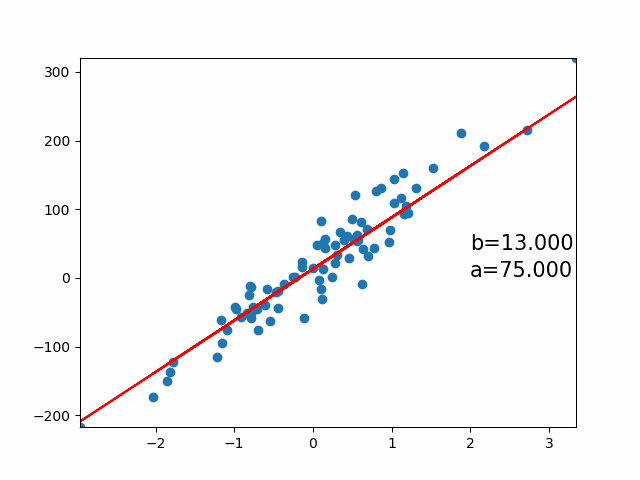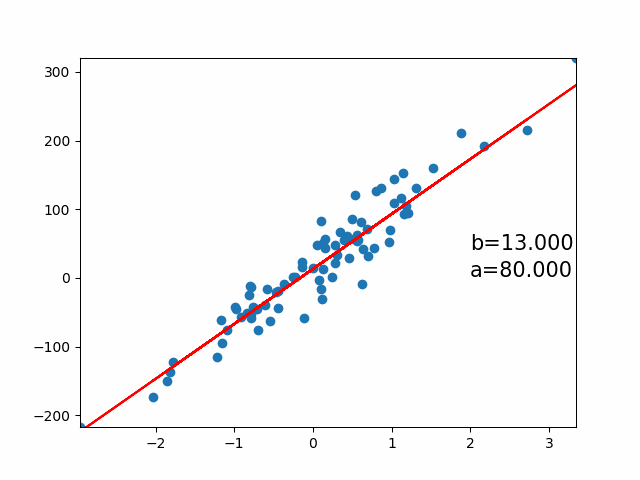
核心思想

通过线性方程拟合数据，最小化预测值与真实值的误差平方和，解决回归问题。
示例：根据房屋面积和房间数量预测房价。
算法流程
1. 初始化模型参数（权重 θ \theta θ 和偏置 θ 0 \theta_0 θ0）。
2. 计算预测值 y ^ = θ T X + θ 0 \hat{y} = \theta^T X + \theta_0 y^=θTX+θ0。
3. 计算损失函数（均方误差，MSE）。
4. 通过梯度下降更新参数，最小化损失。
5. 重复步骤2-4直至收敛。

2. 算法原理与数学推导

数学基础

基于最小二乘法，通过优化均方误差损失函数求解最优参数。
关键公式推导
- 假设函数 ：
  h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n = θ T X h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n = \theta^T X hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn=θTX
- 损失函数（MSE） ：
  J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
- 梯度下降更新规则 ：
  θ j : = θ j − α ∂ J ( θ ) ∂ θ j \theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} θj:=θj−α∂θj∂J(θ)
  其中：
  ∂ J ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)} ∂θj∂J=m1i=1∑m(hθ(x(i))−y(i))xj(i)
  - 对偏置项 θ 0 \theta_0 θ0：
    ∂ J ∂ θ 0 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right) ∂θ0∂J=m1i=1∑m(hθ(x(i))−y(i))
闭式解（正规方程）

当特征矩阵 X X X 可逆时，直接求解：
θ = ( X T X ) − 1 X T y \theta = \left( X^T X \right)^{-1} X^T y θ=(XTX)−1XTy
超参数说明

超参数作用示例值

学习率 α \alpha α 控制参数更新步长 0.01

迭代次数决定训练终止条件 1000

超参数	作用	示例值
学习率 α \alpha α	控制参数更新步长	0.01
迭代次数	决定训练终止条件	1000

3. 评估指标

指标	公式	特点
均方误差 (MSE)	1 m ∑ i = 1 m ( y i − y ^ i ) 2 \frac{1}{m} \sum_{i=1}^m \left( y_i - \hat{y}_i \right)^2 m1i=1∑m(yi−y^i)2	对异常值敏感，数值越小越好
平均绝对误差 (MAE)	$$\frac{1}{m} \sum_{i=1}^m \left	y_i - \hat{y}_i \right
决定系数 ( R 2 R^2 R2)	1 − ∑ i = 1 m ( y i − y ^ i ) 2 ∑ i = 1 m ( y i − y ˉ ) 2 1 - \frac{\sum_{i=1}^m \left( y_i - \hat{y}i \right)^2}{\sum{i=1}^m \left( y_i - \bar{y} \right)^2} 1−∑i=1m(yi−yˉ)2∑i=1m(yi−y^i)2	越接近1表示模型解释力越强

4. 应用案例

经典场景
- 波士顿房价预测：根据房屋特征（房间数、犯罪率等）预测房价中位数。
- 销售额预测：基于广告投入（电视、报纸、广播）预测产品销售额。

实现代码片段

python 复制代码

# 使用Scikit-learn实现
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)

# 预测与评估
y_pred = model.predict(X_test)
print("MSE:", mean_squared_error(y_test, y_pred))
print("R²:", r2_score(y_test, y_pred))

# 输出参数
print("权重:", model.coef_)
print("偏置:", model.intercept_)

5. 面试题

理论类问题
Q1：线性回归的假设条件是什么？
答案：
1. 线性关系：特征与目标变量呈线性关系。
2. 误差独立同分布：残差服从均值为0的正态分布，且相互独立。
3. 同方差性：残差的方差恒定。
4. 无多重共线性：特征之间不存在高度相关性。
Q2：梯度下降和正规方程的区别是什么？
答案：
- 梯度下降：迭代优化，适合大规模数据（时间复杂度 O ( m n 2 ) O(mn^2) O(mn2)），需调学习率。
- 正规方程：直接求解解析解，适合小规模数据（时间复杂度 O ( n 3 ) O(n^3) O(n3)），要求 X T X X^T X XTX 可逆。

编程类问题
Q3：手写梯度下降实现线性回归

python 复制代码

def linear_regression_gd(X, y, alpha=0.01, epochs=1000):
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(epochs):
        y_pred = X.dot(theta)
        error = y_pred - y
        gradient = (1/m) * X.T.dot(error)
        theta -= alpha * gradient
    return theta

6. 扩展分析

算法变种

变种 改进点 适用场景

岭回归 (Ridge) 加入L2正则化，防止过拟合特征多重共线性较强时

Lasso回归加入L1正则化，自动特征选择高维稀疏数据

变种	改进点	适用场景
岭回归 (Ridge)	加入L2正则化，防止过拟合	特征多重共线性较强时
Lasso回归	加入L1正则化，自动特征选择	高维稀疏数据

与其他算法对比

维度	线性回归	决策树回归
可解释性	高（权重明确）	中等（树结构可解释）
非线性拟合能力	弱（需手动特征工程）	强（自动处理非线性）
训练速度	快（闭式解或简单迭代）	中等（需构建树结构）

总结

线性回归是机器学习入门核心算法，需重点掌握：

数学推导：损失函数、梯度下降、正规方程。
应用限制：假设条件不满足时（如非线性关系），需改用多项式回归或树模型。
面试考点：从理论假设到代码实现的全链路理解。