前言
感觉跟回了家一样。
一、线性规划
1.适用场景
实际生活中,肯定存在一类问题,要让我们在约束条件内求怎样安排可以使收益最大或成本最小,即在有限的资源下获得最大收益。线性规划就是在某些线性的约束条件下求解线性目标函数的极值问题。
说人话,就是背包dp。
2.基本概念
首先,要了解决策变量这个概念。决策变量就是问题中需要确定的未知量。拿多重背包举例,决策变量就是每种物品要几件。之后,目标函数就是包含决策变量的函数,求解线性规划问题就是在求目标函数的最值,就是dp表最终格子的数值。约束条件就是每种物品的数量或者背包的大小,在这里一般由等式或不等式表示。
注意,这里约束条件和目标函数必须都是线性的。
3.基本步骤
(1)确定各概念和表达式
首先要做的肯定要确定上述三个概念在实际情境里对应的变量,然后写出目标函数的表达式和约束条件。其中,目标函数中各决策变量的系数可以写成列向量C,即价值向量,然后各个约束条件中各决策变量的系数也可以写成矩阵A,决策变量写成列向量x,即决策向量,那么约束值可以写成常数向量b。由此,我们就可以得到线性规划的矩阵表达式:,其中s.t.表示约束条件。
注意,这里不一定是只有一个目标函数,也可能是多目标规划问题,比如同时要求收益最大和风险最小。多目标规划的求解方法就是转化成单目标规划,方法就是将多目标转化成约束条件进行求解。
(2)求解线性规划
因为python里有封装好的函数,所以直接看代码吧。
4.代码
(1)例题

注意,整数线性规划不适用这个函数。
python
import numpy as np
#线性规划库
from scipy.optimize import linprog
"""
样例一
初始表达式:
max y=20x1+30x2+45x3
s.t.={4x1+8x2+15x3<=100
{x1+x2+x3<=20
{x1,x2,x3>=0
因为封装好的函数默认求最小值,所以需要先对目标函数添符号
min -y=-20x1-30x2-45x3
"""
#价值向量C
C=[-20,-30,-45]
#小于等于的约束条件矩阵
A_ub=[
[4,8,15],
[1,1,1]
]
B_ub=[100,20]
#等于的约束条件矩阵
# A_eq=[]
# B_eq=[]
#决策变量的范围 -> n*2矩阵 -> n为决策变量数,每行包括上界和下界
bound=[[0,None],[0,None],[0,None]]#None为无穷
#求解方法method -> 默认high
#求解
result=linprog(C,A_ub,B_ub,bounds=bound)
print("最优解x:\n",result.x)
print("最小值fun:\n",-result.fun)#注意要取负转成最大值对于线性规划问题,python里的函数求的是目标函数的最小值。那么如果问题里目标函数是求最大值,需要取一个负号转成最小值。不仅如此,这个函数的不等式约束默认小于等于,所以如果是大于等于的情况,也需要将其取负号转成小于等于。
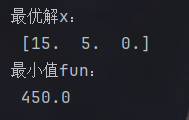
注意因为目标函数取过负号,所以在输出时还要取负号转回来。
(2)投资收益问题

原题其实是一个多目标规划问题,只是通过设置风险度a将这个多目标问题转化成了单目标问题。
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#价值向量
C=[-0.05,-0.27,-0.19,-0.185,-0.185]
#不等式约束矩阵
#np.c_[]按列合并数组,zeros创建一个全零的数组作为第一列,diag创建一个对角阵
A_ub=np.c_[np.zeros(4),np.diag([0.025,0.015,0.055,0.026])]
print("不等式约束矩阵:\n",A_ub)
#等式约束矩阵
A_eq=[[1,1.01,1.02,1.045,1.065]]
B_eq=[1]
#初始化风险度参数a
a=0
a_list=[]
fun_list=[]
#搜索风险度
while a<0.05:
#不等式约束
B_ub=np.ones(4)*a
#范围
bound=[[0,None],[0,None],[0,None],[0,None],[0,None]]
#线性规划
result=linprog(C,A_ub,B_ub,A_eq,B_eq,bounds=bound)
#最优解和最小值
fun=-result.fun#取负转化
#存入列表
a_list.append(a)
fun_list.append(fun)
#步长
a=a+0.001
#可视化
plt.scatter(a_list,fun_list,marker='*',c="r")
plt.xlabel("风险度a")
plt.ylabel("最大收益")
plt.axis([-0.005,0.06,0,0.3])
plt.legend()
plt.show()这个题能得出的最大的提示就是在求解实际问题中,可以适当进行一些假设。比如在这个题里,就需要假设出风险度这个变量,
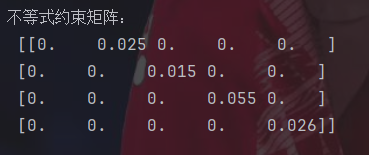
这就是创建了一个对角阵。
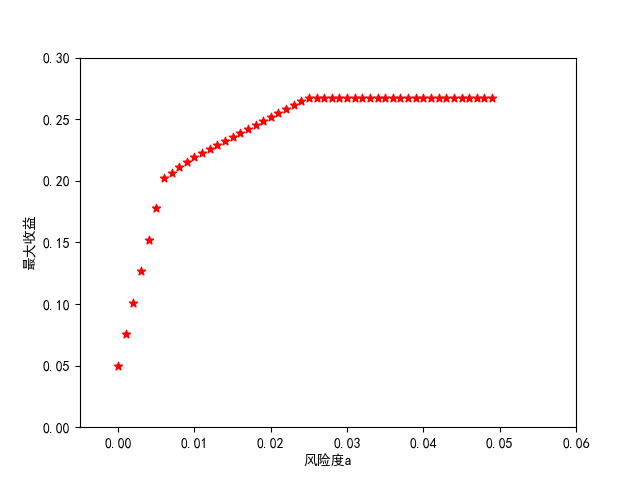
分析可得,再风险度接近零的时候,其实收益是很低的。但随着风险度的增长,收益会先快速增长一段,接着增长速度放缓。最后当风险度达到3%往后收益其实就不太会增长了。
二、蒙特卡洛法
1.适用场景
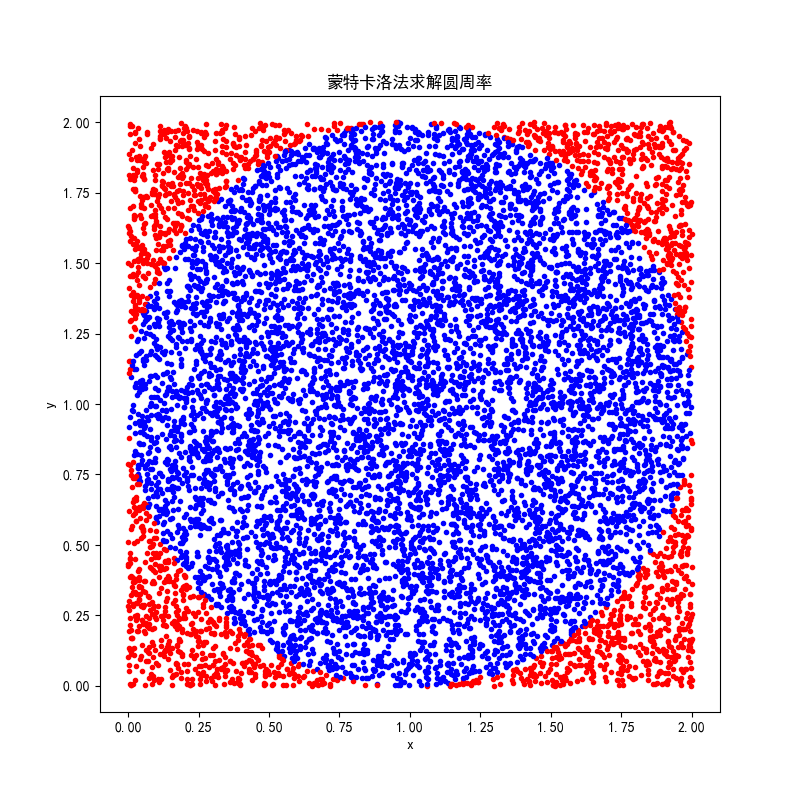
在求解一些难以直接计算的问题时,可以通过随机的形式,通过概率求得近似解。举个例子,在求圆周率π时,可以先作出圆的外接正方形,然后随机往图里撒大量的点。因为圆的面积比上正方形的面积可以推出等于四分之π,所以圆周率π就可以近似看作落在圆内的点数比上总点数。
2.基本概念
蒙特卡洛法又称统计模拟法,可以将求解的问题和概率相联系,从而获得近似解。
3.代码
(1)求圆周率
python
import numpy as np
import matplotlib.pyplot as plt
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#投10000个点
p=10000
#半径
r=1
#圆心
x0,y0=1,1
#在圆内的点
n=0
#可视化
plt.figure(figsize=(8,8))#创建窗口
plt.title("蒙特卡洛法求解圆周率")
plt.xlabel("x")
plt.ylabel("y")
#保持绘图窗口,多次绘图
for i in range(p):
#撒的位置
px=np.random.rand()*2
py=np.random.rand()*2
#判断是否在圆内
if (px-x0)**2+(py-y0)**2<r**2:
plt.plot(px,py,'.',color='b')#圆内点蓝色
n+=1
else:
plt.plot(px,py,'.',color='r')#圆外点红色
#计算
pi=(n/p)*4
print("pi的近似值:",pi)
#横纵坐标单位长度相同
plt.axis('equal')
plt.show()首先就是设置一共要投的点的个数,然后每次随机生成点的坐标,判断在圆内还是圆外,最后计算并生成图像即可。
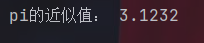
这个还是比较接近的。
(2)三门问题
三门问题讲的就是有三扇门,两扇后是羊,一扇后是车,随机选择一扇获得门后的东西。假如我们想获得汽车,在选择一扇门后,先不展示结果,可以帮你在另外两扇门中排除一个错误选择,那么此时我们是否要更改选择呢?
一般来讲,初见的想法就是反正就剩两扇门,选哪个都是百分之五十的概率,所以更不更改当前的选择都是一样的。但事实并非如此。
python
import numpy as np
#模拟次数
n=100000
#不更改时的获胜次数
a=0
#更改时的获胜次数
b=0
#失败的概率
c=0
for i in range(n):
#生成1,2,3的随机数
x=np.random.randint(1,4)#车在的门
y=np.random.randint(1,4)#选择的门
change=np.random.randint(0,2)#改不改
if x==y:
if change==0:
a+=1
else:
c+=1
else:
if change==0:
c+=1
else:
b+=1
print("不改变时的胜率:",a/n)
print("改变时的胜率:",b/n)
print("失败的概率:",c/n)纯模拟,跟写对数器差不多。

可以发现改变和不改变的胜率差的挺大的。这其实可以理解为,如果不改变主意,想赢的话得一次选中汽车,而改变主意的话得选中羊。那么因为羊有两扇门,车只有一扇门,所以改变主意的胜率会高,且两者的比例近似等于1:2。
三、非线性规划(NLP)
1.适用场景
对于一些要求解xx率的规划问题,因为涉及比率,所以肯定是非线性的。还有对于一些空间里问题,涉及到的方程往往也是非线性的。
2.基本概念
非线性规划就是目标函数里存在非线性函数时的规划方法。非线性规划的最优解可能出现在可行范围内的任意一点,所以只需要会用python求近似解即可。
在非线性规划的问题中,初始值的选择非常重要。因为非线性规划求解出来的是一个局部最优解,如果要求全局最优的话,可以选择给多个初始值,然后从中找一个最优解;也可以选择先用蒙特卡洛法求一个近似的最优解,然后再用这个解作为初始值去求最优解。
3.代码
(1)例题
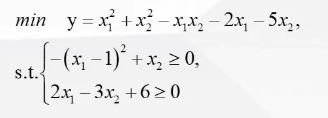
python
import numpy as np
#非线性规划库
from scipy.optimize import minimize
#目标函数 -> 求最小值形式
def func1(x):
return x[0]**2+x[1]**2-x[0]*x[1]-2*x[0]-5*x[1]
#不等式约束 -> 大于等于形式
def nonLinear1(x):
return -(x[0]-1)**2+x[1]
def nonLinear2(x):
return 2*x[0]-3*x[1]+6
#初始值
x=np.array([0,0])
#求解
ans=minimize(func1,
x,
constraints=({'type': 'ineq', 'fun': nonLinear1},
{'type': 'ineq', 'fun': nonLinear2},))
print("默认算法结果:")
print("最优解:",ans.x)
print("最小值:",ans.fun)
#蒙特卡洛法求初始值
n=10000000
#uniform生成区间内均匀分布的随机数
x1=np.random.uniform(-100,100,n)
x2=np.random.uniform(-100,100,n)
fmin=10000000
xMTKL=np.zeros(2)
for i in range(n):
x=np.array([x1[i],x2[i]])
#满足约束条件
if nonLinear1(x)>=0 and nonLinear2(x)>0:
ans=func1(x)
if ans<fmin:
fmin=ans
xMTKL=x
print("蒙特卡洛法找到的初始值:",xMTKL)
#基于蒙特卡洛法的结果
ansMTKL=minimize(func1,
xMTKL,
constraints=({'type': 'ineq', 'fun': nonLinear1},
{'type': 'ineq', 'fun': nonLinear2},))
print("基于蒙特卡洛法的结果:")
print("最优解:",ansMTKL.x)
print("最小值:",ansMTKL.fun)非线性规划的函数默认求最小值,不等式条件默认大于等于形式。
注意非线性规划里要传一个函数。为了减少搜索时间,所以可以考虑先用蒙特卡洛法求一个近似的初始值。

这里可以看到答案变得更精确了。
(2)选址问题
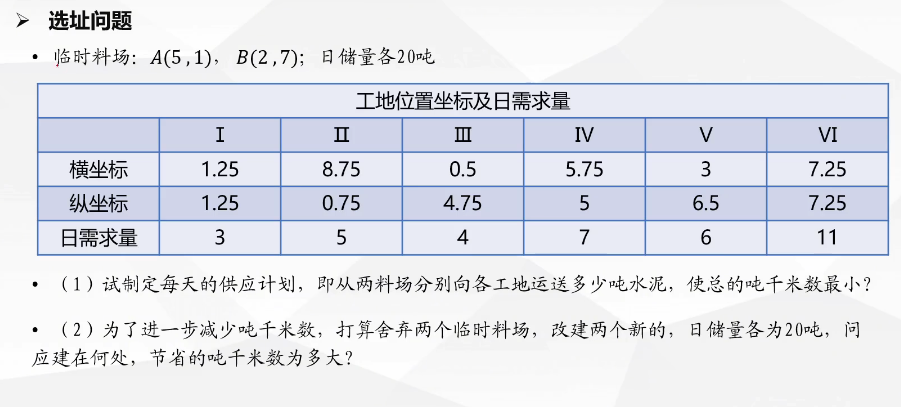
不难发现,表达式为
其中,Xij表示料场j向工地i的运送量,第i个工厂的坐标(Ai,Bi),水泥日用量Di,料场位置(Xj,Yj),日储量Ej。而因为在第一小问里,料场位置是已知的,所以目标函数里根号的部分是个常量,那就是一个线性规划问题。
python
import numpy as np
from scipy.optimize import linprog
from scipy.optimize import minimize
#数据
#工厂横坐标
a=[1.25,8.75,0.5,5.75,3,7.25]
#工厂纵坐标
b=[1.25,0.75,4.75,5,6.5,7.25]
#日需求
d=[3,5,4,7,6,11]
#第一问,线性规划
#变量:每个料场到每个工厂的运输量
#料场坐标
x1,y1=5,1
x2,y2=2,7
#每个工厂到料场1的距离
dis1=[]
for i in range(len(a)):
dis=np.sqrt((x1-a[i])**2+(y1-b[i])**2)
dis1.append(dis)
#到料场2的距离
dis2=[]
for i in range(len(a)):
dis=np.sqrt((x2-a[i])**2+(y2-b[i])**2)
dis2.append(dis)
#合并距离,构成系数向量
f=dis1+dis2
#不等式约束
A_ub=[]
row1=[1]*6+[0]*6
A_ub.append(row1)
row2=[0]*6+[1]*6
A_ub.append(row2)
A_ub=np.array(A_ub)
print("不等式约束矩阵:\n",A_ub)
#不等式约束右侧向量
b_ub=[20,20]
#等式约束
#eye(n)创建n*n的单位矩阵
eye1=np.eye(6)
eye2=np.eye(6)
A_eq=np.hstack((eye1,eye2))
print("等式约束矩阵:\n",A_eq)
#等式约束右侧向量
b_eq=np.array(d)
#范围
bounds=[(0,None)]*12
#求解
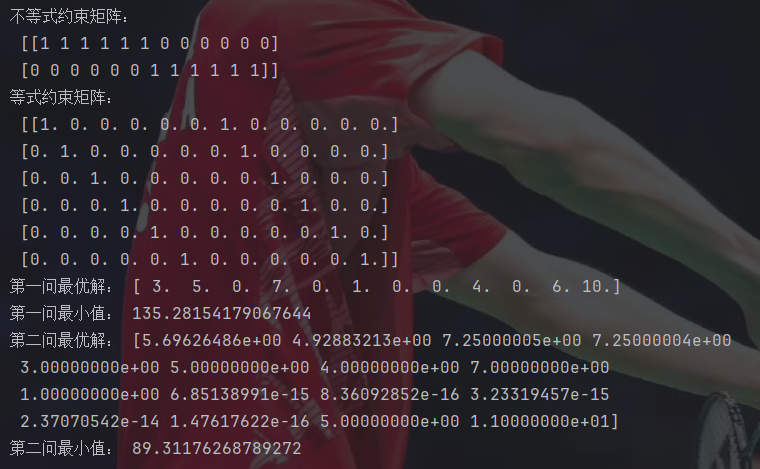
ans=linprog(f,A_ub=A_ub,b_ub=b_ub,A_eq=A_eq,b_eq=b_eq,bounds=bounds)
print("第一问最优解:",ans.x)
print("第一问最小值:",ans.fun)
ans_1=ans.x
#第二问,非线性规划
#变量:两料场横纵坐标和到每个工厂的运输量 -> 4+12=16个
#目标函数
def func(x):
#x[0]和x[1]分别为第一个料场的横纵坐标
#x[2]和x[3]分别为第二个料场的横纵坐标
#x[4:10]为第一个料场到每个工厂的运输量
#x[10:16]为第二个料场到每个工厂的运输量
s=0
j=4
#枚举每个工厂
for i in range(6):
#两料场到该工厂的距离和
s+=x[j]*np.sqrt((x[0]-a[i])**2+(x[1]-b[i])**2)+x[j+6]*np.sqrt((x[2]-a[i])**2+(x[3]-b[i])**2)
j+=1
return s
#不等式约束
def inequality(x):
return np.array([ 20-sum(x[4:10]),20-sum(x[10:16]) ])
#等式约束
def equality(x):
return np.array([x[i+4]+x[i+10]-d[i] for i in range(6)])
cons=(
{'type': 'ineq', 'fun': inequality},
{'type': 'eq', 'fun': equality},
)
#初始值设置为第一问两料场的坐标加上第一问的最优解
x0=np.hstack([[5,1,2,7],ans_1])
bounds=[(0,None)]*16
ans=minimize(func,x0,constraints=cons,bounds=bounds)
print("第二问最优解:",ans.x)
print("第二问最小值:",ans.fun)注意这里第二问的初始值设定为第一问的坐标和第一问算出的结果。
四、整数规划和01规划
1.适用场景
整数规划就是存在必须是整数的决策变量时进行规划的方法。其中,若要求决策变量必须是0或1,那就是01规划了。说人话,就是01背包。
2.经典例题
(1)练级问题

所以公式就是
python
#求解整数规划的库
from pulp import LpMaximize,LpProblem,LpVariable,lpSum,value
#创建问题
problem=LpProblem("Level_Problem",LpMaximize)
#决策变量
x1=LpVariable("x1",lowBound=0,cat="Integer")
x2=LpVariable("x2",lowBound=0,cat="Integer")
x3=LpVariable("x3",lowBound=0,cat="Integer")
#目标函数
problem+=20*x1+30*x2+40*x3
#约束条件
problem+=4*x1+8*x2+10*x3<=100
problem+=x1+x2+x3<=20
#求解
problem.solve()
print("练级规划:")
level=[int(value(x1)),int(value(x2)),int(value(x3))]
print(level)
print("最终等级:")
print(int(value(problem.objective)))这里Integer的意思是整数规划。

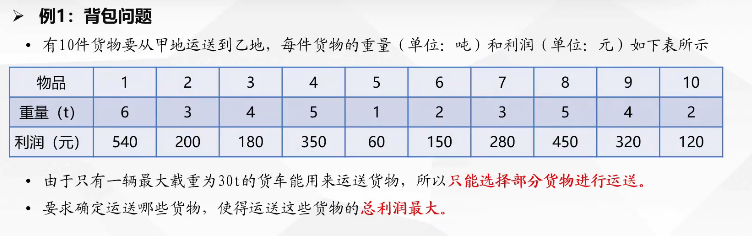
(2)背包问题
是家的感觉!
很简单,定义Pi为利润,Wi为重量,那么公式就是
更改最值类型可得,
python
#求解整数规划的库
from pulp import LpMaximize,LpProblem,LpVariable,lpSum,value
#创建最大值问题
problem=LpProblem("Package_Problem",LpMaximize)
#目标函数系数 -> 收益
profits=[540,200,180,350,60,150,280,450,320,120]
#约束系数 -> 重量
weights=[6,3,4,5,1,2,3,5,4,2]
max_weights=30
#创建决策变量
#cat设置整数规划还是01规划 -> 01:Binary 整数:Integer
x=[LpVariable(f"x{i+1}",cat="Binary")for i in range(10)]
#创建目标函数
problem+=lpSum(profits[i]*x[i]for i in range(10))
#创建约束条件
problem+=lpSum(weights[i]*x[i]for i in range(10))<=max_weights
#求解
problem.solve()
print("选择情况:")
select=[int(value(x[i]))for i in range(10)]#变量值
print(select)
print("最大收益:")
print(value(problem.objective))#目标函数值整数规划函数的约束条件直接+=即可。
(3)指派问题
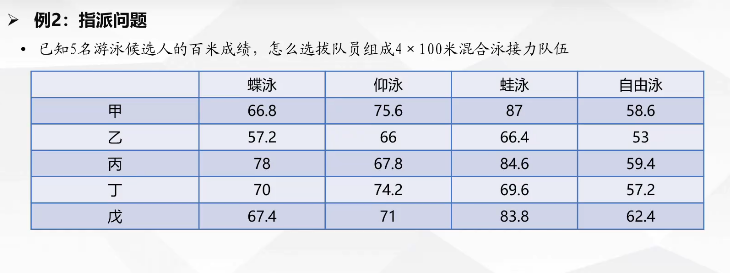
首先对候选人从1到5编号,然后再对泳姿从1到4编号。定义Xij为第i号队员参不参加第j中泳姿,Tij为第i号队员第j种泳姿的时间。所以公式就是
注意前两个约束条件的表达。第一个约束条件的意思是每个人只能选一种泳姿,第二个约束条件的意思是每种泳姿最多只能有一个人参加。
python
import numpy as np
#求解整数规划的库
from pulp import LpMinimize, LpProblem, LpVariable, lpSum, value, LpMinimize
#创建问题
problem=LpProblem("Send_Problem",LpMinimize)
#目标函数系数 -> 时间
c=[66.8,75.6,87,58.6,57.2,66,66.4,53,78,67.8,84.6,59.4,
70,74.2,69.6,57.2,67.4,71,83.8,62.4]
#创建决策变量
x=[LpVariable(f"x{i+1}",cat="Binary")for i in range(20)]
#目标函数
problem+=lpSum(c[i]*x[i]for i in range(20))
#不等式约束
A_ub=[
[1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1],
]
b_ub=[1,1,1,1,1]
for i in range(len(A_ub)):
problem+=lpSum(A_ub[i][j]*x[j] for j in range(20))<=b_ub[i]
#等式约束
A_eq=[
[1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0],
[0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0],
[0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0],
[0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1]
]
b_eq=[1,1,1,1]
#每种泳姿
for i in range(len(A_eq)):
problem+=lpSum(A_eq[i][j]*x[j] for j in range(20))==b_eq[i]#每个选手
#求解
problem.solve()
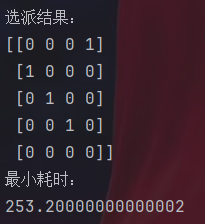
print("选派结果:")
send=np.array([int(value(x[i]))for i in range(20)]).reshape(5,4)
print(send)
print("最小耗时:")
print(value(problem.objective))注意这里系数矩阵的形式。
五、最大最小化模型
1.适用场景
最大最小化算法就是找出最大可能性中的最小值的算法,就是优先考虑最坏的情况,然后让这个情况尽可能好。举个例子,在建立急救中心时,一般就是要考察其到所有地点的最大距离中的最小值。
2.典型例题
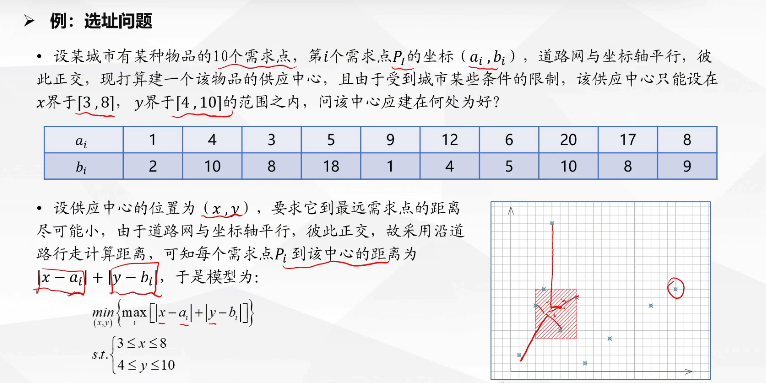
这个题就和上面说的急救中心情况很类似,要求最远距离最小。注意因为这是在网格点上,所以此时距离公式用曼哈顿距离比欧式距离要更合理一点。
python
import numpy as np
#非线性规划库
from scipy.optimize import minimize
#目标函数
def func(x):
#坐标
a=np.array([1,4,3,5,9,12,6,20,17,8])
b=np.array([2,10,8,18,1,4,5,10,8,9])
f=np.zeros(10)
for i in range(10):
f[i]=np.abs(x[0]-a[i])+np.abs(x[1]-b[i])
return f
#目标函数最大值
def maxFunc(x):
return np.max(func(x))
#变量初始值
x0=np.array([6,6])
#决策变量范围
lower_bound=np.array([3,4])
upper_bound=np.array([8,10])
#约束条件
bounds=[(lower_bound[0],upper_bound[0]),(lower_bound[1],upper_bound[1])]
#使目标函数的最大值最小
ans=minimize(maxFunc,
x0,
method='SLSQP',
bounds=bounds,
)
x=ans.x
val=func(x)
print("优化后的坐标:\n",x)
print("去各个点的距离:\n",val)
print("最小的最大距离:\n",np.max(val))方法就是在设置好目标函数后,多设置一个求最大值的函数,然后把这个求最大值的函数传入求解函数,求其最小值即可。
六、多目标规划
1.适用场景
在实际生活中,其实面对的大多数问题都具有多个指标。举个例子,羽毛球比赛的过程中,输赢肯定不是由一个指标决定的。连贯速度,失误率,体能储备等指标都会决定一场比赛的走向,而此时当然不可能要求每个指标都取到最优情况。如果追求连贯速度,那么失误率就会上升,体能储备也会下降得更快;而如果要为第三局做好体能储备,那么速度一定不能冲得太快。多目标规划就是在面对多个目标函数时求解一个最优解的方法。
2.基本概念
首先要介绍三个解的概念:最优解,有效解和满意解。
最优解就是能让所有目标函数都取到最优解的解。在上述例子中,最优解就是连贯又快,失误率又低,体能储备又深不见底。很显然,林丹就是最优解。而一般来讲,最优解是很少存在的,因为不是人人都是林丹。那么此时就需要退而求其次,去求解有效解了。
有效解就是至少能让一个目标函数取得最优的解。那么代入到上面例子中,你可以做到连贯飞快,在场上飞天遁地。此时因为可以快速得分,那么失误率相应高一点也没关系。但这个条件还是太苛刻了,有几个能做到像骆健佑一样飞天遁地,把连贯速度提升到极致的呢?那么此时就需要求一个满意解了。
满意解就是当决策者的期望比较低,给出了每个目标函数的阈值,只要解能满足这个阈值,那么就心满意足了。比如可以不要求速度,失误率和体能某个达到最好,而是退而求其次,每个指标都不是最顶尖,但每个指标都不差,那么依然可以达到一流水平。
3.求解方法
(1)线性加权法
线性加权法就是根据每个目标函数的重要性的不同给其分配不同的权重,然后让对应的目标函数乘以权重,那就能求得总的目标函数。此时就把多目标规划转化成单目标规划了。
(2)约束法
约束法就是根据决策者的喜好,选择一个主要关注的目标函数,然后给其他目标函数设定一个阈值,将其转化为约束条件,从而将多目标规划转化成单目标规划。
这个方法其实就是线性规划里的第二道例题。
(3)理想点法
理想点法就很暴力了,就是先分别求出每个目标函数的最优解的值,称为理想值。然后计算这些目标函数与理想值的差的加权平方和,并使这个加权平方和最小,所求得的解就认为是一个可以接受的解。
4.线性加权法的例题及敏感性分析

敏感性分析就是研究当变量发生改变时,结果的受影响的程度。在上述例子中的体现就是改变设置的权重,观察对结果的影响。
python
import numpy as np
#线性规划
from scipy.optimize import linprog
import matplotlib.pyplot as plt
#两目标函数的多个权重选择
weights=[
(0.4,0.6),
(0.5,0.5),
(0.3,0.7)
]
#约束条件
A_ub=[[-1,-1]]
b_ub=[-7]
#范围
lower_bound=[0,0]
upper_bound=[5,6]
bounds=[(lower_bound[0],upper_bound[0]),(lower_bound[1],upper_bound[1])]
#遍历三种权重
for w1,w2 in weights:
#目标函数系数
c=[w1/30*2+w2/2*0.4,w1/30*5+w2/2*0.3]
#求解
ans=linprog(c,A_ub=A_ub,b_ub=b_ub,bounds=bounds,method="highs")
#结果
x=ans.x
val=ans.fun
#计算
f1=2*x[0]+5*x[1]
f2=0.4*x[0]+0.3*x[1]
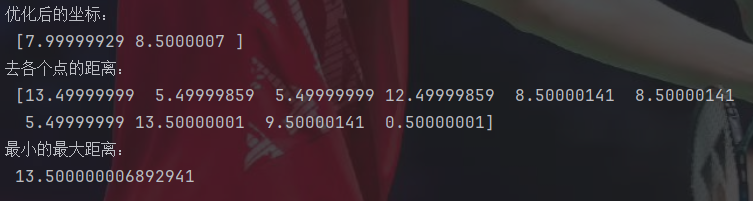
print(f"\n权重:w1={w1},w2={w2}")
print(f"最优解:x1={x[0]},x2={x[1]}")
print(f"函数值:f1={f1},f2={f2}")
print("综合指标:",val)
#敏感性分析
#权重范围
W1=np.arange(0.1,0.501,0.001)
W2=1-W1
n=len(W1)
#初始化
F1=np.zeros(n)
F2=np.zeros(n)
X1=np.zeros(n)
X2=np.zeros(n)
fval=np.zeros(n)
#遍历所有权重
for i in range(n):
w1=W1[i]
w2=W2[i]
c=[w1/30*2+w2/2*0.4,w1/30*5+w2/2*0.3]
ans = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method="highs")
x=ans.x
fval[i] = ans.fun
F1[i] = 2 * x[0] + 5 * x[1]
F2[i] = 0.4 * x[0] + 0.3 * x[1]
X1[i] = x[0]
X2[i] = x[1]
#可视化
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#图1:权重与目标函数的关系
plt.figure()
plt.plot(W1,F1,label="f1")
plt.plot(W1,F2,label="f2")
plt.xlabel("权重")
plt.ylabel("目标函数值")
plt.legend()
plt.title("目标函数值随权重的变化")
plt.grid(True)
#图2:权重与决策变量的关系
plt.figure()
plt.plot(W1,X1,label="x1")
plt.plot(W1,X2,label="x2")
plt.xlabel("权重")
plt.ylabel("决策变量值")
plt.legend()
plt.title("决策变量值随权重的变化")
plt.grid(True)
#图3:权重和综合指标的关系
plt.figure()
plt.plot(W1,fval,label="fval")
plt.xlabel("权重")
plt.ylabel("综合指标值")
plt.title("综合指标值随权重的变化")
plt.legend()
plt.grid(True)
plt.show()这里用的是线性加权法,取了三个权重分别计算答案。之后敏感性分析就是设置权重范围后循环搜索。
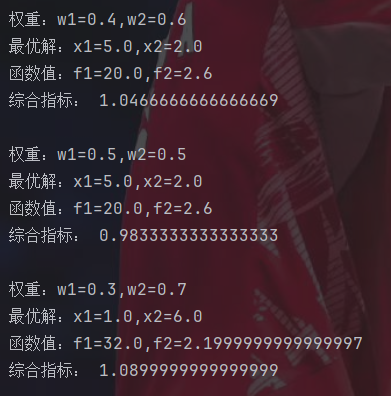
从目标函数随权重的变化这个图里可以看到,在权重为0.3到0.35之间时,成本会发生大幅度下降,但污染不会有太大变化。
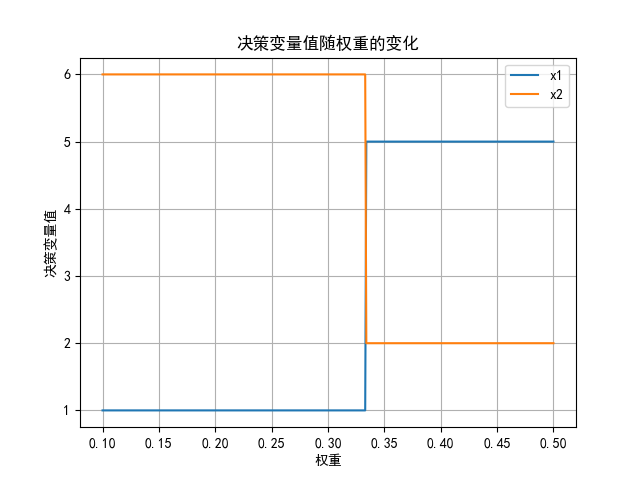
从这个图里可以看出,当权重取在0.3到0.35之间,两产品的生产数量会发生大幅变化。
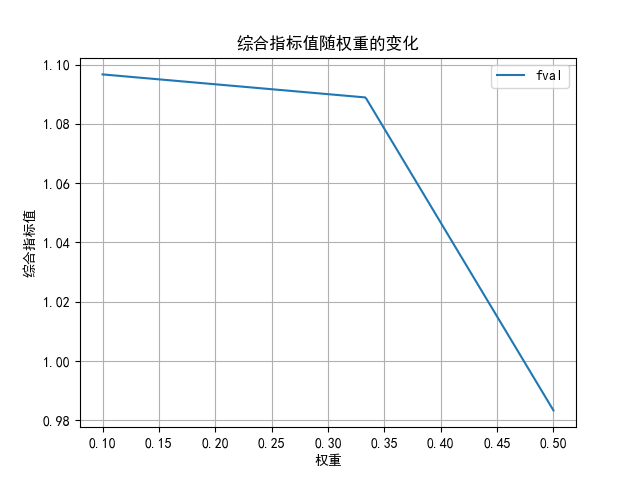
而从这个图里可以看出,随着权重提升,综合指标先小幅度下降,后大幅度下降。说明权重在0.3到0.35这个区间内,权重对结果的影响较大。
七、动态规划
回家了。

水题()
python
import numpy as np
#面值:2,5,7
def solve(n):
coin=[2,5,7]
dp=np.zeros(n+1)
dp[0]=0
for i in range(1,n+1):
dp[i]=1e9
for j in range(len(coin)):
if i>=coin[j]:
dp[i]=min(dp[i],dp[i-coin[j]]+1)
if dp[n]==1e9:
return -1
else:
return dp[n]
print("输入要拼的金额:")
n=int(input())
ans=solve(n)
print(ans)没啥好说的,模板题。
八、图论
这给我干哪来了,这还是数学建模吗?
1.绘图
python
#绘图库
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
#创建图结构
G = nx.Graph() #无向图 有向图nx.DiGraph()
#添加节点
nodes = [
(1, {"color": "red", "size": 300}),
(2, {"color": "red", "size": 300}),
(3, {"color": "red", "size": 300}),
(4, {"color": "red", "size": 300}),
(5, {"color": "red", "size": 300})
]
G.add_nodes_from(nodes)
#添加带权重的边
edges = [
(1, 2, {"weight": 2.5}), #边1-2,权重2.5
(1, 3, {"weight": 1.8}),
(2, 3, {"weight": 3.0}),
(3, 4, {"weight": 2.0}),
(4, 5, {"weight": 1.2}),
(1, 5, {"weight": 0.7})
]
G.add_edges_from(edges)
#可视化
plt.figure(figsize=(10, 8))
#布局算法
pos = nx.spring_layout(G, seed=42, k=0.15) # k控制节点间距
#提取节点颜色和大小属性
#data=True返回数据而非下标
#下划线_忽略idx
node_colors = [data["color"] for _, data in G.nodes(data=True)]
node_sizes = [data["size"] for _, data in G.nodes(data=True)]
#提取边权重
edge_weights = [data["weight"] for _, _, data in G.edges(data=True)]
#绘制节点
nx.draw_networkx_nodes(
G,
pos,
node_color=node_colors,
node_size=node_sizes,
alpha=0.9
)
#绘制边
nx.draw_networkx_edges(
G,
pos,
width=[w * 1.5 for w in edge_weights], #线宽反映权重
edge_color="gray",
alpha=0.7
)
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#绘制标签
nx.draw_networkx_labels(G, pos, font_size=12)
edge_labels = {(u, v): f"{d['weight']:.1f}" for u, v, d in G.edges(data=True)}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
#添加标题和图例
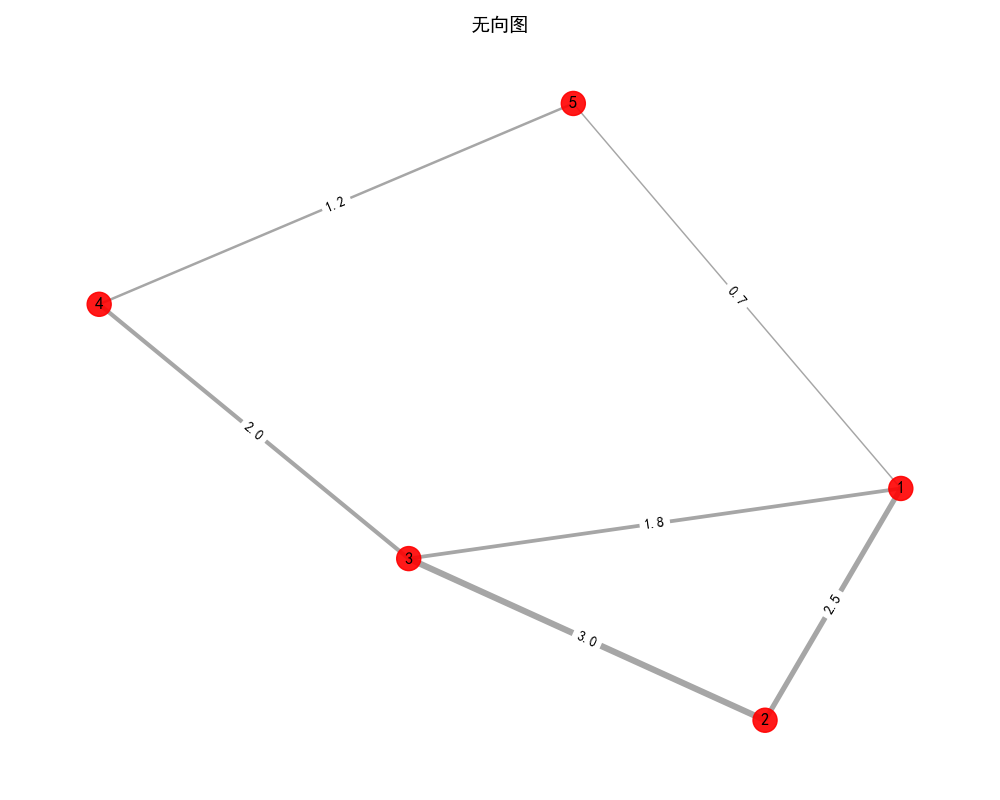
plt.title("无向图", fontsize=14)
plt.axis("off") # 关闭坐标轴
plt.tight_layout()
plt.show()注意这里的布局算法,为了防止每次生成的图都不一样,所以要把随机种子给设置好。
2.最短路径算法
(1)Dijkstra算法
(2)Floyd算法
数据结构与算法:A星、Floyd、Bellman-Ford及SPFA
3.最小生成树
总结
最熟悉的一次。