1.概念
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)是一种多属性决策分析方法,中文常译为"逼近理想解排序法"。其核心思想是:通过计算各方案与"正理想解"(最优解)和"负理想解"(最劣解)的相对距离,对方案进行排序。距离正理想解越近且距离负理想解越远的方案越好。
说白了就是要离最优解最近,离最劣解最远
最优解就是在各个指标都达到了备选方案中的最佳值,比如原神有的角色有数值但不好看,有的角色好看但是数值不高,最优解就是又有数值又好看,最劣解就相反
eg:评选原神最佳主C
|------|-----|-----|-----|-------|
| 角色 | 数值 | 手感 | 颜值 | 人气 |
| 那维莱特 | 9.3 | 8.8 | 8.5 | 427.9 |
| 斯柯克 | 9 | 8.6 | 9 | 419.8 |
| 阿蕾奇诺 | 9 | 8.9 | 8.7 | 503.1 |
| 玛薇卡 | 9.1 | 8 | 8 | 459.9 |
(前三个为小程序值,最后为角色pv播放量,单位w,均为正向值)
2.基本步骤
1.将原始矩阵正向化
把所有指标都转化成极大型指标(也就是越大越好)
比如抽取一个角色所用的抽数肯定是越少越好,因此要把这种指标正向化
|-------|-------------|----------|
| 指标 | 特点 | 例子 |
| 极大型指标 | 越大越好 | 成绩,颜值 |
| 极小型指标 | 越小越好 | 抽卡抽数,坏品率 |
| 中间型指标 | 越接近某个值越好 | |
| 区间型指标 | 在某个区间范围内比较好 | 体温,BMI |
|-------|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 指标 | 转化公式 |
| 极大型指标 | / |
| 极小型指标 | ,其中
是转化后指标,max是指标最大值,x是指标值 |
| 中间型指标 | 是一组中间型序列,最优值是
,
|
| 区间型指标 | 是一组区间型序列,最佳区间是[a,b],
|
2.正向矩阵标准化
保证不同指标都在一个数量级
标准化公式(每一个元素/其所在列平方和开方)
标准化后还要加上权重,权重确定方法有层次分析法等,这里默认四种指标权重相同
3.计算得分并且归一化
找到标准化矩阵Z
1.定义每一列(每一种指标)
最大值
最小值
2.定义第i个评价对象与
最大值的距离
最小值的距离
3.计算未归一化的得分
(显然Si在0到1之间,且Di+越小Si越大,表示接近最大值)
4.得分归一化并百分制
3.代码
Matlab
%判断是否需要正向化
X=input('指标矩阵A=');
[n,m]=size(X);
disp(['共有' num2str(n) '个评价对象',num2str(m) '个评价指标']);
Judge = input(['这' num2str(m) '个指标是否需要正向化处理,需要输入1,不需要输入0:']);
if Judge==1
Position=input('请输入需要正向化处理的指标所在的列,例如第2,3,6列现需要处理,那么输入[2,3,6]:');
disp('请输入需要处理的这些列的指标类型(1:极小型,2:中间型,3:区间型)');
Type=input('例如:第2列是极小型,第3列是区间型,第6列是中间型,需要输入[1,3,2]');
for i=1:size(position,2)
X(:,Position(i))=Positivization(X(:,Position(i)),Type(i),Position(i));
end
disp('正向化后矩阵X=');
disp(X);
end
%正向化
Z=X ./ repmat(sum(X .* X) .^ 0.5,n,1);%repmat默认是每一行相加,最终是一个行向量,然后复制n行1列
disp('标准化矩阵 Z = ');
disp(Z)
D_P = sum([( Z - repmat(max(Z),n,1) ).^2],2).^0.5;
D_N = sum([( Z - repmat(min(Z),n,1) ).^2],2).^0.5;
S=D_N ./ (D_P+D_N);
disp('最终得分');
stand_S=100*S/sum(S)
%[sorted_S,index]=sort(stand_S,'descend');%排序函数,默认升序,加descent是降序
Matlab
function [posit_x]=Positivization(x,type,i)
if type==1
disp(['第' num2str(i) '列是极小型,正在正向化'] );
posit_x=Min2Max(x);
disp(['第' num2str(i) '列极小型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
elseif type==2
disp(['第' num2str(i) '列是中间型,正在正向化'] );
best=input('请输入最佳值');
posit_x=Mid2Max(x,best);
disp(['第' num2str(i) '列中间型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
elseif type==3
disp(['第' num2str(i) '列是区间型,正在正向化'] );
up=input('请输入区间上界');
low=input('请输入区间下界');
posit_x=Inter2Max(x,up,low);
disp(['第' num2str(i) '列区间型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~');
else
disp('type不存在除1,2,3外的类型');
end
end
Matlab
function [posit_x]=Min2Max(x)
posit_x = max(x)-x;
end
function [posit_x]=Mid2Max(x,best)
M=max(abs(x-best));
posit_x=1-abs(x-best)/M;
end
function [posit_x]=Inter2Max(x,a,b)
M=max([a-min(x),max(x)-b]);
posit_x=zeros(size(x,1),1);
for i =1:size(x,1)
if x(i)<a
posit_x(i)=1-(a-x(i))/M;
elseif x(i)>b
posit_x(i)=1-(x(i)-b)/M;
else
posit_x(i)=1;
end
end
end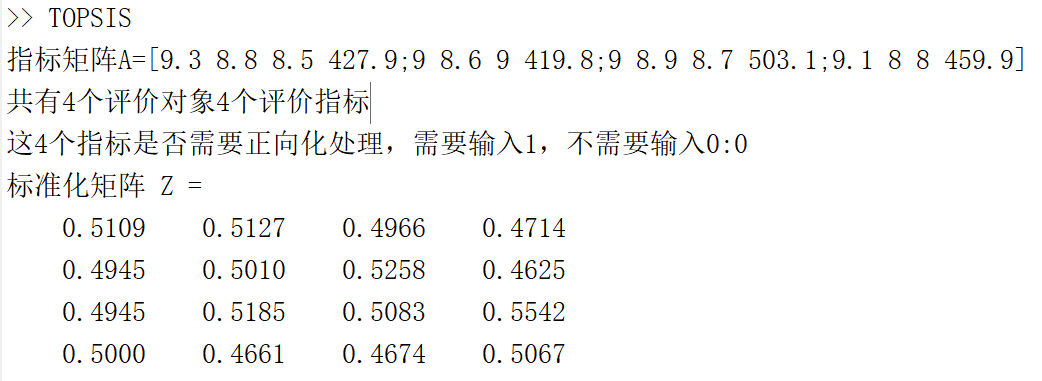

附加权重代码
Matlab
disp('标准化矩阵 Z = ');
disp(Z)
% ===== 新增权重部分 =====
Weights = input('请输入各指标的权重(如[0.3,0.4,0.3]): ');
if abs(sum(Weights) - 1) > 1e-6
error('权重之和必须为1!');
end
Z = Z .* Weights; % 加权标准化矩阵
disp('加权标准化矩阵 Z_weighted = ');
disp(Z);
% =========================
D_P = sum([( Z - repmat(max(Z),n,1) ).^2],2).^0.5;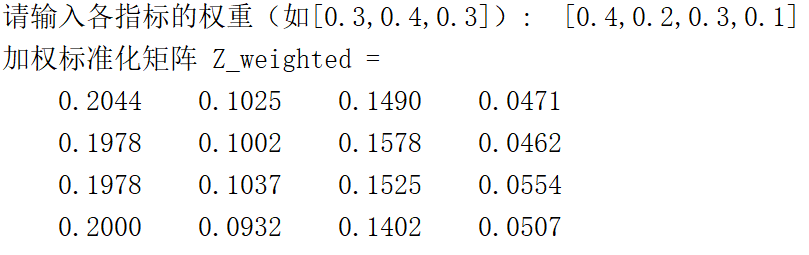

最终结果:(牢玛输麻了)
|------|-----|-----|-----|-------|-------|-------|
| 角色 | 数值 | 手感 | 颜值 | 人气 | 评分 | 加权后评分 |
| 那维莱特 | 9.3 | 8.8 | 8.5 | 427.9 | 20.23 | 26.73 |
| 斯柯克 | 9 | 8.6 | 9 | 419.8 | 21.26 | 30.23 |
| 阿蕾奇诺 | 9 | 8.9 | 8.7 | 503.1 | 41.97 | 33.82 |
| 玛薇卡 | 9.1 | 8 | 8 | 459.9 | 16.53 | 9.20 |