目录
1.程序功能描述
深度学习中的长短期记忆网络(LSTM) 通过独特的门控机制解决了传统循环神经网络(RNN)的 "梯度消失" 问题,能够有效捕捉长时序数据中的依赖关系,成为当前网络流量测量(尤其是流量预测、异常检测)的主流技术之一。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
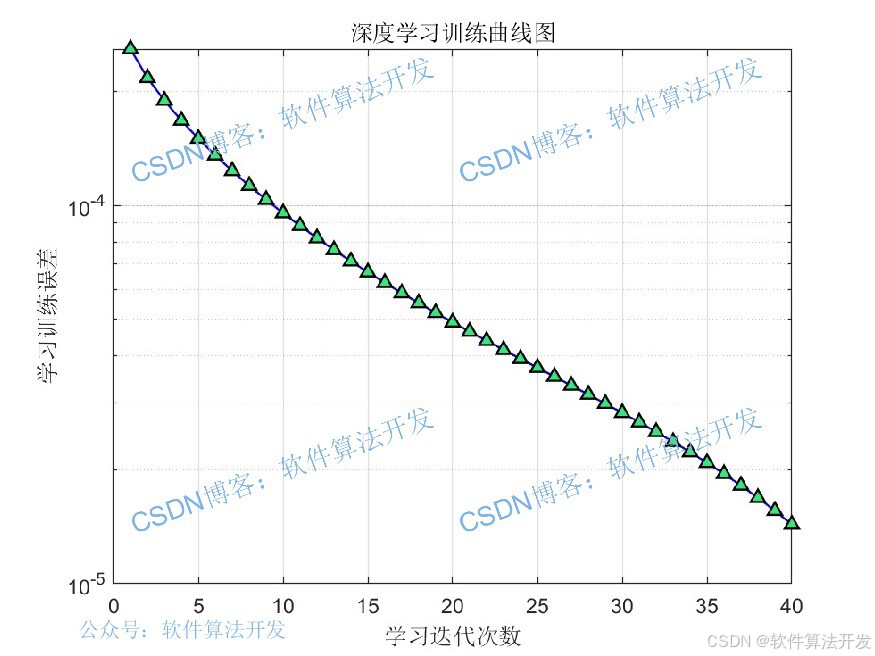
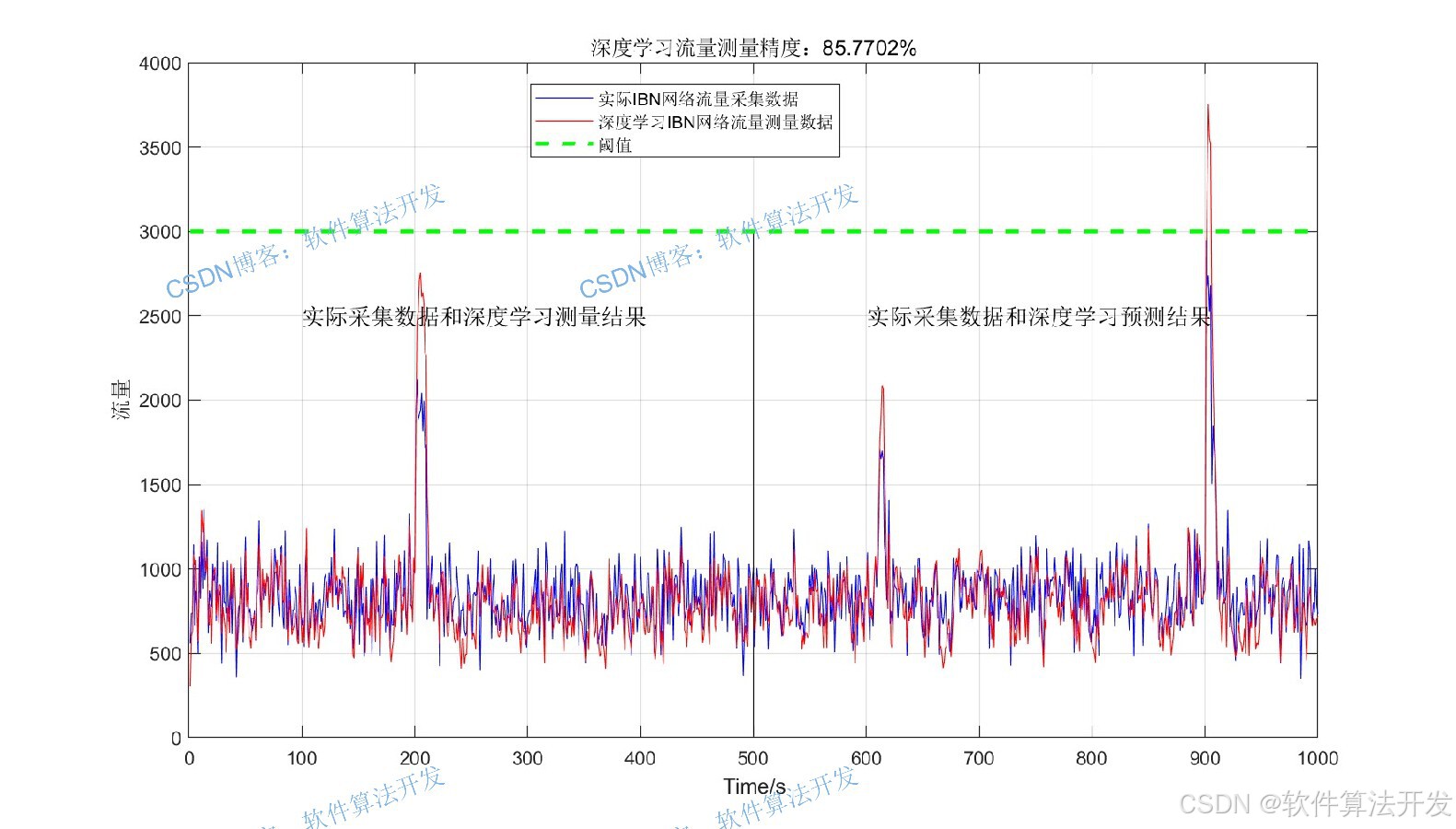
3.部分程序
figure;
plot(IBN_testflow,'b');
hold on
plot(pre,'r');
grid on
xlabel('Time/s');
ylabel('流量');
hold on
plot(500*ones(1,300),10:10:3000,'k');
text(100,2500,'实际采集数据和深度学习测量结果','fontsize',12);
text(600,2500,'实际采集数据和深度学习预测结果','fontsize',12);
hold on
plot(3000*ones(1,1000),'g--','LineWidth',2);
accacy = 100-100*mean(abs(IBN_testflow(1:end)-pre(1:end))./IBN_testflow(1:end));
legend('实际IBN网络流量采集数据','深度学习IBN网络流量测量数据','','阈值');
accacy
title(['深度学习流量测量精度:',num2str(accacy),'%']);
save LSTM.mat accacy IBN_testflow pre
012_055m4.算法理论概述
基于LSTM的网络流量测量流程可分为模型设计、模型训练、模型评估、部署应用核心步骤,每个步骤均需结合网络流量的时序特性与LSTM的模型特点进行针对性设计,以下详细解析各步骤的目标、操作及数学建模。根据网络流量测量的任务目标(如流量预测、异常检测),设计LSTM 模型的网络结构,核心包括"输入层→LSTM 层→全连接层→输出层",同时需选择激活函数、 dropout策略等。
| 网络层 | 作用 | 维度设计(基于步骤 3.1.4 示例) |
|---|---|---|
| 输入层 | 接收时序序列输入 | (None, T, d_x)=(None, 12, 5) |
| LSTM 层(1 层) | 捕捉长时序依赖,输出隐藏状态 | 隐藏单元数dh=64,输出维度(None, 12, 64) |
| LSTM 层(2 层) | 加深模型复杂度,捕捉更复杂的流量模式 | 隐藏单元数dh=32,输出维度(None, 12, 32) |
| 全局平均池化层 | 减少参数数量,避免过拟合 | 输出维度(None, 32) |
| 全连接层 1 | 映射隐藏状态到中间特征空间 | 神经元数 = 16,输出维度(None, 16) |
| 全连接层 2(输出层) | 映射到预测目标(未来 K 个时间步的流量) | 神经元数 = K=1,输出维度(None, 1) |
5.完整程序
VVV