【C++进阶系列】：万字详解红黑树（附模拟实现的源码）

🔥 本文专栏：c++

🌸作者主页：努力努力再努力wz

💪 今日博客励志语录 ：允许自己停顿，但不要被困在原地；尊重内心的疑问，但别让它蒙蔽勇气。此刻的犹豫不是弱点，而是你与灵魂的对话------ 倾听它，然后相信：无论朝哪个方向走，你都会成为光的一部分

★★★ 本文前置知识：

引入

在此前的学习中，我们学习了二叉搜索树，那么我们知道二叉搜索树这个数据结构能够高效的查找存储在二叉搜索树中的元素，通过二叉搜索树的左小右大的性质来实现，但是在极端情况，二叉搜索树可能会退化成链表的形态，导致二叉树的深度过高，从而增高了二叉搜索树的查找的时间复杂度

所以我们希望在满足二叉搜索树的左小右大的性质前提条件下，那么尽可能的压缩二叉树的高度，从而减少遍历的次数，而之前我介绍的AVL树就是在二叉搜索树的基础上，借助平衡因子以及旋转来优化了二叉搜索树本身的结构，成功的压缩了二叉搜索树的高度，而今天要将的就是另一种数据结构红黑树，其和AVL树一样，那么它所做的也是在满足二叉搜索树的前提下，尽可能的压缩二叉搜索树的高度，那么它的压缩和AVL的实现又有何不同，那么接下来，我将会带你认识红黑树这个数据结构，从原理到用代码模拟实现，两个维度来带你全面解析红黑树

红黑树

原理

颜色标记

那么我们知道红黑树本质上是一棵二叉搜索树，但是它在二叉搜索树的结构的基础上做出的优化和改变，那么从红黑树的名字，我们也可以感受得到，其与颜色有着密切的关系，或者说和红和黑这两种颜色有着密切的关系，那么事实上，红黑树确实将每一个节点进行一个颜色标记，那么在红黑树中的所有节点，那么其都有一个颜色标记，每一个节点其不是红色就是黑色

那么提到标记这个词，我们自然会联想到AVL树中学到的平衡因子，那么AVL树中每一个节点也都具备一个平衡因子，那么平衡因子的引入，就是为了确认每一个节点作为当前局部二叉搜索树的根节点的时候，那么其左右子树的高度差是否超过1，因为平衡因子值的计算就是右子树高度减去左子树的高度，那么如果平衡因子的的绝对值如果大于1，说明了当前节点，其作为根节点的局部的二叉搜索树是不平衡的，需要立刻进行调整

而当前我们虽然不知道红黑树中这个所谓颜色标记的意义，但是根据此前的AVL树，那么我们可以推导：这里的颜色标记一定和二叉搜索树的平衡有关，毕竟红黑树核心也是要压缩二叉搜索树整体的高度，使其趋于平衡，所以红黑树的颜色标记就肯定这里的平衡有关，而说到平衡，那么此刻我们的重心便转移到了对于红黑树来说，那么其要求或者对平衡的定义是什么，一旦知道了红黑树对平衡的定义，我们就便能够理解器颜色标记的意义

那么对于红黑树来说，那么其要求或者要满足的平衡就是：根节点到空节点的最长路径的长度不超过根节点到空节点的最短路径的长度的2倍 ，并且对于其左右子树也得递归满足该性质

比如这里，对于根节点A来说，最短路径是左侧的路径，其长度为1，那么最长路径是最右侧的路径，其长度为2，那么满足性质，那么其左右子树也都同样满足，那么此时这棵是就是达到了红黑树要求的平衡

所以每当我们插入一个新的节点的时候，那么插入的新节点会让根节点到新节点这条路径的长度加一，意味着每次插入一个新的节点，可能会导致根节点到新节点这条路径长度大于了根节点到其空节点的最短路径的两倍

所以每次向红黑树中插入一个新的节点，可能会破坏红黑树中的平衡，所以这里我们就得想办法检查插入新节点是否会破坏红黑树的平衡

那么检查的方式有两种，第一种就是直接暴力的检查，采取深度优先遍历，计算根节点到其每一个空节点的路径的长度，计算出所有路径的长度之后，在比较得到最小和最长的长度，然后再检查最长路径的长度是否超过最短长度的两倍，然后再重复同样的方式递归的检查其左右子树，那么正常人都不会选择这种方式，因为这种方式要不断的往下遍历每一个子树的所有路径，那么付出的时间代价肯定很大

那么第二种方式就是这里红黑树的方式，也就是通过颜色标记来巧妙的限制了根节点到叶子节点的最长路径不超过最短路径的两倍，那么这里是如何来限制的呢？

就是通过红黑树满足其他额外的几点性质：

性质一：红黑树中的节点要么为红要么为黑

性质二：整颗树的根节点必须为黑色

性质三：不能出现连续的红色节点

性质四：从任意一个节点出发，到达底部的空叶子节点的每一个路径上的黑色节点个数要完全相等

性质五：空叶子节点必须是黑色

那么这里红黑树的空叶子节点还有一个专业术语，其也被称之为NIL节点，NIL节点都默认为黑色

而对于第三点这里我这里在额外补充一下，那么所谓不能出现连续的红色节点的意思是：如果当前节点是红色，那么其左右孩子节点（假设存在左右孩子）一定不能为红色，只能为黑色，并且其父节点也只能为黑色，如果当前节点为红色，但其其父节点或者左孩子节点或者右孩子一旦为红色，那么就与该性质相违背

那么通过这五点性质来一起约束就可以得到红黑树中的根节点到NIL的最长路径不超过最短路径的2倍，只要满足了这五点性质，那么你自动的就满足根节点到NIL节点的最长路径不超过最短路径的2倍，意味着我们不用显示手动的检查并且计算当前的根节点到NIL的最长路径是多少以及最短路径是多少，那么只需要检查前面四点性质是否满足即可

那么现在读者唯一的问题可能就是，你怎么证明这五点性质满足，那么就能保证当前根节点到NIL节点的最长路径一定不超过最短路径的2倍呢，所以接下里我就来证明一下，为什么满足这5点性质就能够保证平衡

那么我们现在知道了第4条性质，就是当前根节点出发，到达底部的每一个NIL节点的路径上对应的黑色节点个数要相等，那么我们知道如果一个节点是红色，那么它不会对其所处的路径上的黑色节点的个数有任何的贡献，只会仅仅增加路径的长度，所以这里我们就考虑一个最极端的情况，那么根节点到NIL节点中的最长路径中的最长应该是什么样子

而根据刚才的分析，那么我们知道红色节点不会为其所属路径的黑色节点个数有任何贡献，只会增加路径的长度，所以我们要让一个路径尽可能的长，那么该路径一定得尽可能的包含越多的红色节点，那么为什么这里是包含尽可能更多的红色节点而不是黑色节点呢？那么根据性质4我们知道，根节点到NIL节点的每一个路径中包含的黑色节点的个数要相等

那么意味着这如果你当前路径包含更多的黑色节点，那么其他路径也必须包含相同数量的黑色节点，因为要保证每一个路径上的黑色节点的个数要相等，但是如果你当前路径添加红色节点，那么当前路径的黑色节点的个数没变，那么你不用在其他路径添加任何节点，因为没有破坏性质4

但是由于性质3存在，也就是一条路径上不能出现连续的红色节点，所以你不能无脑的往一个路径一直插入红色节点，所以这里我们就能够知道最长路径的一个极端情况是什么样子了：

也就是该最长路径上的节点的颜色是红黑交替的，那么所谓的红黑交替就是两个红节点中间夹着一个黑节点，或者两个黑节点中间夹夹着一个红节点，那么要做到这种红黑交替，那么只能是红色节点的个数和黑色节点的个数是相同的，那么才能保证红色节点沿途往上的节点是黑色，沿途往下的节点也是黑色

那么如果红色节点比黑色节点多一个，那么我们可以画图或者脑海中想象，那么此时其余N-1个红色节点之间会夹了N-1个黑色节点，但最后会有一个红色节点空出来，因为这里的N-1个黑色节点包含一个NIL节点，而NIL节点只能在末尾，后面不能还有节点，所以最后空出来红色节点前面会连接一个红色节点，导致出现连续的红色节点，所以这里只能红节点和黑节点的数量相同，才能保证红黑交替
理想红黑交替情况红黑红黑红 NIL 红节点数: 3
黑节点数: 3
路径长度: 6

那么这种情况就是最极端的情况，也就是最长路径中的最长路径，那么此时我们再来看最短路径的极端情况，那么我们知道红色节点不会对该路径上的黑色节点的个数有任何的贡献，所以一旦包含红色节点，那么该路径长度会增加，所以这里最短路径的极端情况就比较容易想出，那么就是该路径全部都是黑色节点，那么此时这就是最短路径的极端情况，也就是最短中的最短路径

所以假设当前有一个红黑树，那么其根节点到NIL的最长路径和最短路径都是我刚才说的极端情况，那么这里我假设最长路径的中的红色节点个数为N，那么其黑色节点的个数也一定为N，那么这里由于性质4，那么每一个路径上的黑色节点的个数要相等，也就是得保证每一个路径的黑色节点个数都得为N，那么意味着最短路径的长度是N-1，因为其是最短路径是全黑节点
红黑交替路径全黑路径 D
E
F
G
NIL
B
C
NIL
A
全黑路径
路径长度: 3
黑色节点个数: 3
(最短路径) 红黑交替路径
路径长度: 5
黑色节点个数: 3
(最长路径)

而此时最长路径为2N-1，最短路径为N-1，那么在这种极端情况下，那么最长路径中的最长路径还是没有超过最短路径的2倍，那么这里我们已经证明了最长中的最长路径都不会超过最短中的最短路径的2倍，而事实上，一个根节点的最短路径一定是大于或者等于这个最短路径的极端情况，而最长路径也一定是小于或者等于这个极端情况，而刚才我们证明了最大值不超过最小值的2倍

min <=最短<=最长<=max

min=N-1, max=2N-1

所以这里只要最长路径和最短路径在这个最大值和最小值之间，那么其一定满足最长路径不超过最短路径

所以这里红黑树就通过颜色标记以及这几点性质巧妙的共同约束且保证了红黑树的平衡性

插入

那么知道了红黑树颜色标记的意义之后，那么这里我们再来了解红黑树插入新节点的原理，而之前我就说过，红黑树的节点的颜色不是红色就是黑色，所以这里我们往红黑树中新插入一个节点，那么其也有两种情况，要么新插入的节点为红色，要么新插入的节点为黑色，那么这里如果我们选择将新插入的节点为红色，那么我们知道插入的节点是红色节点是不会破坏性质4的，因为其不会为该路径的黑色节点的个数有任何的贡献，但是可能会破坏性质3，也就是如果当前插入的节点的父节点也是红节点，那么会出现连续的红节点，但是如果其父节点为黑色节点，那么就没有任何的影响

而如果此时你插入的节点是黑色节点，那么就不是可能会破坏，而是必然会破坏性质4，因为插入的黑节点会让当前路径上的黑色节点的个数加一，而其他路径的黑色节点个数都没变

所以这里我们知道不管我们新插入的节点的颜色设置为红色还是设置为黑色，那么都有造成红黑树性质破坏的风险，那么也会造成破坏性质的风险，那么我们就得想办法恢复调整

但是如果你插入的是黑色的话，那么重新恢复性质的难度要比插入红节点来重新恢复调整要难很多，所以我们规定新插入的节点是红色，而后文我会讲插入的节点如果是红色，那么如何恢复调整的方法，那么一旦理解了插入红节点四如何调整，那么你就能明白插入黑节点来重新恢复是比插入红节点困难很多，所以这里我先买一个伏笔，那么后文我会简单讲插入黑节点是如何恢复，那么让读者认识这里设计者为什么不选择规定插入的节点是黑色

那么插入红节点就好比打碎了房子上的一个窗户，只需要对这局部简单修补一下就可以了，而插入黑节点就好比打断了支撑整个房子的横梁，那么可不是简单的修复就能解决的，所以这里规定了新插入的节点的颜色只能为红色

变色

由上文我们知道了新插入的节点的颜色一定得为红色，那么此时我们先来引入具体的一个简单的模型，那么假设这里有一棵局部的满足红黑树性质的二叉搜索树，那么其根节点为A，左孩子为B，右孩子为C，其中左右孩子都为红节点，那么这里我们要在B的左侧插入一个新节点D

那么在插入之前，这里父节点B为红色，那么根据性质3，不能出现连续的红色节点，那么刚开始，我没给根节点A的颜色，但我们可以根据性质3，知道根节点A的颜色一定为黑色，因为其孩子节点为红色

而此时新插入的节点D在B的左侧，并且其颜色为红色，而其父节点B也为红色，那么这里出现了连续的红色节点，那么破坏了红黑树的性质，那么我们就得想办法恢复性质，那么恢复性质的核心就是让父节点B变成黑色
A B C D

但是这里仅仅将父节点B变成黑色，那么此时会让父节点B到其底部的NIL节点的所有路径的黑色节点的个数加一，而右侧根节点C到其底部的NIL节点的黑色节点的个数没变，所以这里将父节点B变成黑色，那么会破坏性质4

而这里我们为了便于表述，那么这里我们将根节点到其底部的NIL节点的所有路径上的黑色节点个数称之为黑高，那么该子树的黑高为N，代表这当前子树的根节点到达底部的NIL节点的所有路径的黑色节点个数为N

那么计算一棵局部二叉搜索树的黑高Hb，那么我们可以引入该计算公式，借助性质4：

若根节点为黑色，那么以根节点的局部二叉搜索树的黑高HB为： Hb=1+Hb（左子树） 或者 Hb=1+Hb（右子树）

若根节点为红色，那么以根节点的局部二叉搜索树的黑高:Hb=Hb(左子树)或者Hb=Hb(右子树)

其中 Hb(左子树)==Hb(右子树)

那么我们知道在插入红节点之前，那么根节点A的左子树的原本的黑高为1，这里的1对应的就是底部的NIL节点，其余都为红，那么对于A的右子树也一样，其A的右子树的黑高也为1，那么此时新插入一个红节点，我们为了避免出现连续的红节点，只能将父节点B变成了黑色，那么会导致左子树的整体的黑高变为了2，而右子树的整体的黑高还是1，那么此时以A为根节点的局部的二叉搜索树，其左右子树的黑高不相等，那么这里以A为根节点的局部的二叉搜索树必然不平衡

而根据上文的公式，我们知道我们如果改变一个子树中的根节点的颜色，那么会影响该子树整体的黑高，如果子树的根节点原本是红色，那么将其变成黑色，那么其子树整体的黑高会加一，而如果原本是黑色，将其变成红色，反之子树整体的黑高会减一，而这里左侧子树的黑高比右侧高一，为了让左右子树的黑高相等，那么这里我们只能让右子树的根节点，右红色变成黑色，此时让右子树整体的黑高和左子树的黑高相等，都为2

那么此时我们看似让这棵局部的子树恢复了性质，也就是没有出现连续的红节点，并且其左右子树的黑高相等，那么意味着其根节点A的局部的二叉搜索树满足了性质3与性质4，达到了平衡

但是这里注意根节点A与其左右子树又会整体作为根节点A的父节点O的一侧的子树，那么插入之前，那么其A为根节点所在一侧的子树的黑高也一定与父节点O的另一侧子树的黑高相等

在插入之前，我们可以计算得到A作为根节点，整体的黑高是2，因为其左子树和右子树的黑高都为1，而A为黑节点，而这里我们刚才对A的左右孩子都变色，将其都变成了黑色，让左右子树的黑高都变成了2，最终让A为根节点的整颗局部二叉搜索树的黑高变成了3，那么O的另一侧子树的黑高不相等，所以这里我们虽然这里以A为根节点的局部二叉搜索树平衡，但是却破坏了沿途的祖先节点的平衡，所以这里我们得出A为根节点的整颗局部二叉搜索树的黑高不变

而上文就说过，根节点的颜色的改变会影响整颗局部的二叉搜索树的黑高，而这里原本根节点是黑色，那么这里我们就得将其变成红色，那么这一变色，会让A为根节点的整颗局部二叉收货数的黑高减一，那么抵消了左右子树的黑高整体的增加，从而维持了这棵局部的二叉搜索树的黑高不变，保证了其不会破坏往上的祖先节点为根节点的局部二叉搜索树的平衡
B C A D

但是这里还有一个坑，我们这里如果将父节点B和叔叔节点C变成黑色，而根节点A变成红色，而如果A往上还有祖先节点，并且其也为红色，那么这里意味着还得往上继续调整得到的颜色冲突

所以这里我们就可以引出一个抽象模型，针对这里变色调整的所有的情况，那么该模型还是以节点A还是作为该局部二叉搜索树的根节点，节点A的左孩子为B，右孩子为C，B和C都为黑节点，那么这里B的左孩子D为红色，B的右子树为E，D的左右子树为F和G，而右孩子C的左右子树为K和H

那么由于左孩子B和右孩子C都为红，根据性质，我们知道根节点A只能为黑色
A B C D E F G H K

圆形为节点，方形为子树

由上文，我们知道这里我们如果这里节点D为红色，那么其父节点也为红色，需要利用变色来调整，那么在该模型中，那么我们可以看到这里局部的二叉搜索树中有连续的红节点，但是这个连续的红节点可能是对应上文所讲的那个场景，D可能是新插入的节点，其位于底部，那么D的左子树F和右子树G就为空，但这里的D也可能是上文说的经过一系列的变色，往上调整导致D的颜色为红色，与父节点B颜色冲突，那么这里的D的左右子树F和G就不一定为空

至于D究竟是什么情况以及其左右子树的高度和形态，我们并不关心，那么这里的抽象模型只是用来概括这里所有的情况，并且给出一个统一的解决方案，后文我都会用这种抽象模型来讲解

那么对于这个模型的关键点就在于B的兄弟节点为红色，那么不管D是位于B的左子树还是右子树中，以及B是位于A的左侧还是右侧，我们只要将D的父节点B和D的叔叔节点C都变成黑色，然后让祖父节点A变成红色，那么此时就能够让以A为根节点的整个局部二叉搜索树平衡，那么证明也很简单，那么上文我证明了D在B的左子树中，其能保证以A为根节点的局部二叉搜索树平衡并且不会影响祖先节点的平衡，那么这里我就证明一下D在B的右子树中，采取同样的处理方式，也依然能够能够让A为根节点的局部的二叉搜索树平衡并且不会影响祖先节点的平衡，那么证明过程和上文一样，不复杂：

那么假设A的左子树的黑高为N，那么A的右子树的黑高也为N，而由于A是黑节点，那么A作为根节点的局部的二叉搜索树的整体的黑高为N+1，那么这里由于左子树的根节点B为红节点，那么B的左子树的黑高也是N，同理其B的右子树的黑高也是N，那么右子树的根节点为D，其为红节点，那么其左右子树的黑高也为N，而A的右子树的根节点C为红节点，右子树整体的黑高为N，那么C的左右子树的黑高为N
A B C D E黑高：N F 黑高：N G黑高：N H黑高：N K黑高：N

那么这里将A的左右孩子也就是B和C由红色变成黑色，那么此时A的左子树整体的黑高为N+1，右子树的黑高也为N+1，那么A为根节点的整体的局部的二叉搜索树的黑高是H+2，那么这里让节点A变成红色，那么整体的局部的二叉搜索树的整体的黑高减一，变为了N+1，和之前一样
左子树黑高：N+1 A B C D E黑高：N F黑高：N G黑高：N H黑高：N K黑高：N 右子树黑高：N+1

所以不管是B是位于右侧还是左侧，以及D是位于B的左侧还是右侧，那么其都可以同样可以按照这种方式计算证明，那么都能得到正确的结果，所以此时对于这种场景，也就是当前节点为红色，父节点也为红色并且叔叔节点存在也为红色，那么采取的就是变色，让父节点和叔叔节点变成黑色，祖父节点变成红色

单旋+变色

那么有了上文的抽象的模型之后，那么此时我们再来引入另一个抽象的模型，还是有一颗局部的二叉搜索树，那么其根节点为A，A的左孩子为B，A的右孩子为C，只不过这里B为红节点，C为黑节点，然后B的左孩子为D，那么D的左子树为E，右子树为F，那么B的右子树为G，C的左子树为H，右子树为K

那么由于左孩子B为红节点，那么D的祖父节点A一定为黑节点，而这里如果D为红节点，那么其父节点B也为红节点，那么这里出现了连续的红节点，那么就要进行调整，那么在这个模型下，那么我们能不能按照上文的做法，也就是仅仅通过变色从而让此时A作为根节点的局部二叉搜索树达到平衡呢
左子树黑高：N A
B
C
D
E
黑高：N F
黑高：N G
黑高：N H
黑高：N-1 K
黑高：N-1 右子树黑高：N

那么这里还是一样，我们假设A的左子树整体的黑高为N，右子树的整体的黑高为N，那么由于根节点A是黑色，那么A为根节点整体的局部二叉搜索树的黑高为N+1，那么这里左子树的根节点B为红色，那么其B的左子树的黑高为N，B的右子树G的黑高为N，而这里B的左子树的根节点D为红节点，那么D的左子树和右子树的黑高也为N

而右子树整体的黑高为N，而右子树的根节点C为黑节点，所以C的左子树和右子树的黑高为N-1

这里如果我们还是想上文那样通过简单的变色，也就是将父节点B变成黑色，那么这里左子树的黑高整体变为了N+1，但是这里叔叔节点C已经是黑色节点了，那么这里如果将其变成红色，反而会让右侧子树整体的黑高变成N-1，所以这里是无法通过变色来解决的

但是这里由于D和其父节点B都是连续的红节点，这里调整的核心肯定还是是将父节点B变成黑色，但是父节点变成黑色会导致左侧整体的黑高增加，而右侧的黑高不变，所以这里我们就得通过旋转，而在该场景下，则是通过右单旋，那么之前讲解AVL树的时候，我们知道，所谓的右单旋其实就是给右侧增加一个节点，那么该节点就是原本的根节点，而，让左侧减少一个节点，减少的就是左子树的根节点，其被提升成了整棵树的根节点

而这里右旋会让父节点B提升成为根节点，然后让原本的根节点A添加进右子树，作为B的右孩子，并且将B的右子树交给A，作为其左子树，那么右旋完，我们再来计算一下，此时旋转后的以B为根节点的局部二叉搜索树的黑高
右旋操作右旋调整后 B
D
A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1 初始状态 A
B
C
D
G
黑高：N E
黑高：N F
黑高：N H
黑高：N-1 K
黑高：N-1

那么此时B为红节点，那么虽然左子树少了一个节点，但是该节点是红节点，所以左子树整体的黑高不变，那么还是N，但是右子树此时添加进了一个根节点，并且将B的黑高为N的右子树，交给了A作为其左子树，而原本的根节点A是黑节点，所以此时旋转后的右子树整体的黑高为N+1，那么左右子树的黑高不相等，那么此时就要么将左子树的黑高增加或者右子树的黑高降低

那么如果让左子树的黑高增加，也就是让此时左子树的根节点D变成黑色，从而左子树整体的高度为N+1，但是之前整个局部的二叉搜索树的黑高为N+1,那么这里为了维持原来整体的高度，那么这里得将根节点B变成红色，而被提升作为整颗树的根节点B之前就是红色，所以不用再变为红色

那么让左子树的黑高增加，确实让旋转后以B为根节点的局部二叉搜索树的达到平衡并且不会破坏祖先节点的平衡，但是这里将旋转后的的根节点为红色，那么这里会造成与祖先节点的颜色冲突，如果祖先节点存在且为红色，那么还得向上继续调整
将D变为黑色
左子树黑高增加根节点B为红色
可能与祖先节点冲突可能冲突 P
红色 B
红色其他子树颜色调整后 B
D
A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1 右旋后初始状态 B
D A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1

所以更优的做法则是我们采取降低右子树的黑高，也就是将旋转后的右子树的根节点A变成红色，然右子树的黑高变成N，此时左右子树的黑高都是N，但是原本的二叉搜索树的整体的黑高为N+1，那么此时就得将提升成根节点的B，由红色变成黑色，而这种方式不仅满足了此时局部二叉树的平衡，并且还不会与沿途向上的祖先节点产生颜色冲突，因为此时根节点的颜色已经为黑色，所以这里我们采取第二种方式也就是降低右子树的高度
将A变为红色
右子树黑高降低为N 将B变为黑色
整体黑高恢复为N+1 最终平衡状态 B
D
A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1 降低右子树黑高 B
D
A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1 右旋后初始状态 B
D
A
E
黑高：N F
黑高：N G
黑高：N C
H
黑高：N-1 K
黑高：N-1

那么此时我们知道了旋转加变色能够使得当前的局部的二叉搜索树达到平衡，那么这里我们再来分析为什么这里会采取旋转，也就是旋转的意义是什么

我们知道在当前场景下，那么如果我们改变父节点的颜色，让父节点由红色变成黑色，那么会使得父节点所在的一侧，也就是左子树的黑高大于右子树，那么这里我们无法改变右子树的黑高，因为右子树的根节点为黑色，所以无法通过着色来让右子树增高，所以这里的旋转将黑色的根节点添加进右子树，同时让左子树为红色的根节点提升到提升到整颗树的根节点，相当于此时旋转减少了左侧的黑高，但是却增加了右侧的黑高，所以这里我们就得通过着色来抵消左侧增加的黑高，让左右两侧的黑高平衡，那么这就是旋转+变色的目的

那么这里还有另一种情况，也就是节点B在根节点的右侧，并且红色节点D在B的右侧，那么和刚才上面所说的模型是对称的，那么处理的方式就是同样，左单旋+变色，那么至于后序的证明过程就不在过多赘述

而这里还要注意一个特殊的场景，之前我们说的都是父亲的兄弟节点存在的情况，那么要么为红，要么为黑，那么这里还有一个场景就是父节点的兄弟节点不存在，由于父节点的兄弟节点不存在，那么意味着祖父节点有的一侧的子树为空，那么为空一侧的子树的黑高为1，而根节点左右两侧的子树的黑高要相等，那么另一侧子树的黑高也为1，这里的1对应的就是底部的NIL节点，那么意味着另一侧非空的子树只能全部为红节点，而红节点不能连续，祖父节点非空一侧的子树只能有一个孩子，其为红节点
特殊场景: 叔叔节点不存在祖父节点
父节点
NIL
当前节点
NIL
空子树黑高: 1
(只有NIL节点) 非空子树黑高: 1
(只能有一个红节点)

而这里另一侧的子树都为空，那么这里肯定不能仅仅变色来解决，因为一侧的子树都没有非空的节点了，而空节点NIL只能为黑色，是不允许变色的，所以这里只能旋转，然后让根节点添加到被旋转的一侧，然后将另一侧子树的根节点提升到整个局部的二叉搜索树的根节点，而旋转后，和上文说的一样，那么还需要变色来抵消旋转一侧增加的黑高，所以该场景可以和上文说单旋+变色的模型归为一类，因为都是同一种处理方式

双旋+变色

那么接下来我们在在上面的模型做一个改变，那么还是一个局部的二叉搜索树，那么根节点为A，那么根节点的左孩子节点为B，那么根节点A的右孩子节点为C，其中B是红节点，C是黑节点，那么B的右孩子为D，D的左子树为E，D的右子树为为F，B的左子树为G，C的左子树为H，其右子树为K

若节点D是红节点，那么还是一样，这里出现了连续的红节点，那么核心还是将其父节点B从红色变色成黑色，那么有了上文的经验，我么知道这里无法仅仅通过变色来解决，那么需要配合旋转，那么这里我们能不能通过右单旋加变色来让以A为根节点的局部的二叉搜索树达到平衡呢

那么我们就来验证一下，那么这里假设根节点A的左子树的黑高为N，那么右子树的黑高也同样为N，由于左子树的根节点B为红色，那么B的左子树的黑高为N，B的右子树的黑高也为N，那么B的右子树的根节点D为红，那么这里D的左右子树的黑高还是为N

而对于右子树来说，那么右子树的根节点C为黑，那么C的左右子树的黑高都为N-1
A
B
C
G
黑高：N E
黑高：N F
黑高：N D
H
黑高：N-1 K
黑高：N-1

这里我们先右单旋，将左子树的根节点B提升到整棵树的根节点，将原本的根节点A作为B的右孩子，并且B的黑高为N的右子树会交给A，作为其左子树，那么此时我们计算一下右单旋过后，左子树整体的黑高，那么左子树整体的黑高就是原本B的左子树的黑高，为N
B
G
黑高：N A
D
E
黑高：N F
黑高：N C
H
黑高：N-1 K
黑高：N-1

而此时旋转过后，那么A作为了右子树的根节点，那么A的左右子树的黑高都是N，那么此时右子树整体的黑高是N+1，那么有的读者认为接下来的步骤就是变色即可，但是此时我们发现这里A接收了B的右子树，而B的右子树的根节点D是红节点，如果此时我们将右单旋过后的根节点B变成黑色，然后其右孩子A变成红色，那么这里对于右子树来说，那么右子树的根节点A和其左孩子D都是红节点，此时就会出现连续的红节点

并且我们可以发现，这里右旋加变色后的形态，其实就是之前的初始状态的一个对称，如果此时我们再左单旋加变色就能恢复之前的原始状态

那么之所以导致出现这种状况的原因，就是因为被旋转下来的根节点A会接收其被提升到整个局部二叉搜索树的根节点的节点B的右子树，而其中右子树的根节点是红节点

而旋转，就是将原本的根节点添加到被旋转的一侧，而让另一侧的左孩子或者右孩子节点提升到根节点
以B为轴左旋左旋后状态 A
D
C
B
F
黑高：N G
黑高：N E
黑高：N H
黑高：N-1 K
黑高：N-1 左旋前状态 A
B
C
G
黑高：N D
E
黑高：N F
黑高：N H
黑高：N-1 K
黑高：N-1

所以这里我们再整体右旋之前，那么我们先对B为根节点的局部的二叉搜索树整体左旋，那么此时B的右子树的为红色的根节点D会被提升作为该局部的二叉搜索树的根节点，而原本的根节点B则会被添加进左子树中，并且接收D的左子树，作为其右子树

那么有的读者在这就会有疑问，根据上文，他知道对于一个局部的二叉搜索树单旋，会破坏该局部二叉搜索树的平衡，还需要变色来进行补偿，那么这里对B为根节点的局部的二叉搜索树进行旋转，那么会不会也同样会破坏以B为根节点的局部的二叉搜索树的平衡？

但是我们仔细观察以B为根节点的局部二叉树，其根节点B是红节点，并且其右孩子D也为红节点，那么这里左单旋，添加到左子树的节点B是红节点，并且提升到根节点的节点D也是红节点，而红节点是不会对子树贡献任何的黑高，所以这里一侧添加一个红节点，一侧减少一个红节点，不会影响左右子树的整体的黑高，所以这里以B为根节点的局部二叉搜索树的左单旋，是不要变色来进行补偿的，除非这里一侧添加或者减少的是黑节点，才需要变色进行补偿，让该局部二叉搜索树平衡

那么这里旋转完成后，那么为红色的节点D被提升到左子树的根节点，而在被提升之前，由于D是红节点，那么根据性质3，D的左右孩子节点只能是黑色节点，所以这里我们再对A为根节点的局部的二叉搜索树右旋时，我们就可以放心的将D的黑高为N右子树交给A，作为其左子树，，并且将红节点D提升到整个局部二叉搜索树的根节点
D
B
A
G
黑高：N E
黑高：N F
黑高：N C
H
黑高：N-1 K
黑高：N-1

而此时双旋之后的局部二叉搜索树的左子树的黑高就是D的左子树的黑高，为N

而此时旋下来的节点A为黑色，那么节点A的左右子树的黑高都为N，那么此时右子树的整体的黑高为N+1，所以这里需要变色来补偿，抵消右侧新增的黑高，也就是将旋转后的节点A由黑色变为红色，而此时A的左右孩子都是黑节点，不会像刚才，出现连续的红节点

那么这里变色完后，左右子树的整体的黑高相等，都为N，但此时整棵局部的二叉搜索树的黑高为N,因为被提升到根节点的节点D为红色，而原本整体的局部二叉搜索树的黑高为N+1，所以这里需要将节点D变为黑色，来维持整个二叉搜索树的黑高不变
D
B
A
G
黑高：N E
黑高：N F
黑高：N C
H
黑高：N-1 K
黑高：N-1

那么另一种对称的场景的处理也是相似，那么就是B在根节点的右侧，而节点D在B的左子树，那么就是右左双旋加变色，那么具体证明过程和刚才一样，这里就不再赘述了

总结

那么这里我们就可以总结前面说的这几种模型了：

那么第一种就是当前节点为红色，并且父节点也为红色且父节点的兄弟节点存在且为红，那么这里就直接变色处理，将祖父节点变成黑色，父节点和父节点的兄弟节点变成黑色

第二种是当前节点为红色，父节点也为红色且父节点的兄弟节点为黑，那么这个情况要分类，那么分类和之前AVL树判断单旋还是双旋是一样的

第一类就是当父节点位于与祖父节点的左侧并且当前节点位于父节点的左侧或者父节点位于祖父节点的右侧且当前节点位于父节点的右侧，更间接的话就是LL型或者RR型，就单旋加变色，变色就是将旋转后的根节点变成黑，旋转一侧的子树的很节点变成红色，并且父节点的兄弟节点不存在也是归为这一类，采取同样的处理方式

第二类就是父节点位于祖父节点的左侧，当前节点位于父节点的右侧或者父节点位于祖父节点的右侧，当前节点位于父节点的左侧，也就是LR型或者RL型，那么采取的处理，就是双旋加变色，其中变色就是将双旋后的当根节点变成黑色，第二次旋转一侧的子树的根节点变成红色

补充

由上文我们知道了红黑树的原理，并且我们知道了当插入红节点之后，如果出现连续的红色节点，我们如何通过变色或者旋转加变色的方式来调节平衡，那么这里我们就可以解答上文埋下的伏笔，也就是为什么新插入的节点规定为红色而不能规定黑色，那么要理解这一点，我就直接给出一个模型，来让读者见一下，如果我硬要插入的节点是黑色，那么我如该何调整，来恢复性质4，也就是根节点到每一个NIL节点的路径上的黑色节点个数相等

那么这里模型很简单，就是一个根节点A，其左孩子为B，右孩子为C，那么根节点A为黑色，左右孩子都为红色，那么这里我们要在B的左侧插入一个为黑色的节点D

那么这里插入之前，那么我们可以计算左右子树的黑高，以A为根节点的左子树的黑高为1，右子树的黑高为1，这里的1对应就是底部的黑色的NIL节点，同理对于以B为根节点的局部二叉搜索树，那么B的左右子树的黑高也为1
插入黑色节点D 插入黑色节点D后 A
B
C
D
NIL
NIL
NIL
NIL
NIL
B为根节点的局部二叉搜索树黑高不平衡:
B的左子树黑高: 2
B的右子树黑高: 1 插入前状态 A
B
C
NIL
NIL
NIL
NIL
整棵二叉搜索树的黑高: 2
左子树黑高: 1 右子树黑高：1

那么这里在B的左子树插入了一个黑节点，此时B的左右子树的黑高不相等，那么这里B的左子树的黑高为2，右子树的黑高为1，那么这里就要调整以B为根节点的局部二叉搜索树的平衡，让其左右子树的黑高相等，那么这里就通过变色：让D变成红色，B变成黑色，此时让B的左右子树的黑高都为1，B的左右子树的黑高相等，但是插入之前，B为根节点的整体的黑高为1，而此时整体的黑高变为了2，那么会导致沿途往上的A为根节点的局部二叉搜索树不平衡

变色之后，A的左子树的黑高为2，右子树的黑高为1，这里我们就要继续调整以A为根节点的局部二叉搜索树的平衡，此时我们有两种调整方案：

第一种还是像刚才一样，只变色，也就是让C变成黑色，然后此时A的左右子树的黑高相等，但是如果这里A是整棵树的根节点，那么此时就结束，但是如果A不是整棵树的根节点，而是这棵树的某一个局部的二叉搜索树的根节点，那么其会一直影响往上沿途的祖先节点，让祖先节点的左右子树不平衡，那么要就全局的调整，调整到整棵树的根节点

而第二种方案则是旋转加变色，这里我们可以右单旋，此时黑节点B作为了该局部二叉搜索树的根节点，然后A添加进了右子树作为B的右孩子节点，那么此时我们将A变成红色，那么这里左右子树的黑高都相等，都为1，并且整体局部的二叉搜索树的黑高为1，和插入之前一样

但是却引入了连续的红节点，所以这里为了解决连续的红节点，那么经过上文的讲解，那么想必读者知道接下来该怎么做了，而第二种方案也明显比第一种方案好，根据我们上文所讲的原理我们可以知道，因为不用涉及到全局的调整，可以沿途调整到中间的某个祖先节点结束

而这个模型只是插入黑节点的一个冰山一角，那么我还没有引入其他插入情况的模型，那么单单从这一个简单的模型我们就知道了插入黑节点的调整比插入红节点要复杂很多，而插入红节点，那么无非面对的就三种情况，叔叔节点存在且为红，叔叔节点存在且为黑，叔叔节点不存在，这三种场景都有一套固定对应的解法来解决，所以这就是为什么规定新插入的节点只能为红色

模拟实现

经过上文理解了红黑树的原理，接下来我们再来模拟实现一个红黑树

首先我们得先定义出红黑树的节点，也就是定义一个RBTreeNode模板类，那么该模板类需要封装一个pair元组作为数据域，因为红黑树是key-value模型，所以这里的模版参数得有两个，除了数据域，这里还得有三个指针域，分别指向左孩子的left指针以及右孩子的right指针和父节点的parent指针，最后还得有一个颜色标记，那么这里我们使用一个枚举变量，然后将黑色和红色定义为枚举常量来实现这里的颜色标记，其中要注意的是这里RBTreeNode中的成员变量要用public修饰，因为后面的RBTree模板类会封装一个指向红黑树根节点的指针，并且会在成员函数中直接访问节点的指针，来修改连接关系，需要我们在类外直接访问到RBTreeNode中的成员变量

其次这里RBTreeNode支持无参的构造函数，那么将指针域初始化为nullptr，将元组设置为默认值，而带参的构造函数则是接收一个元组，用来初始化RBTreeNode的元组，而这里由于规定新插入的节点颜色都是红色，所以这里给颜色标记都设置为红色即可

cpp 复制代码

enum  color
{
	BLACK,
	RED
};
template<typename key,typename val>
class RBTreeNode
{
public:
	RBTreeNode<key, val>* left;
	RBTreeNode<key, val>* right;
	RBTreeNode<key, val>* parent;
	std::pair<key, val> _pair;
	color _col;
	RBTreeNode()
		:_col(RED)
		, left(nullptr)
		, right(nullptr)
		, parent(nullptr)
		,_pair(std::make_pair(key(),val()))
	{

	}
	RBTreeNode(const std::pair<key,val>& p)
		:_col(RED)
		, left(nullptr)
		, right(nullptr)
		, parent(nullptr)
		,_pair(p)
	{

	}
};
template<typename key,typename val>
class RBTree
{
private:
	typedef RBTreeNode<key, val> Node;
	Node* root;
    ..............................
};

构造函数

那么这里RBTree的构造函数有两个版本，第一个版本就是无参的构造函数，那么就是构建一个空的红黑树，那么根节点为nullptr，而第二个就是带参的构造函数，接收一个元组来初始化根节点

cpp 复制代码

	RBTree()
		:root(nullptr)
	{

	}
	RBTree(const std::pair<key, val>& p)
		:root(new Node(p))
	{
		root->_col = BLACK;
	}

插入insert函数

insert函数的实现逻辑，我们可以大致分为两个部分，第一个部分就是借助二叉搜索树左小右大的性质，遍历这棵红黑树，找到插入的位置以及新插入节点的父节点，再为新插入的节点开辟空间，并且与父节点连接

cpp 复制代码

	if (root == nullptr)
	{
		root = new Node(p);
		root->_col = BLACK;
		return;
	}
	Node* cur = root;
	Node* parent = nullptr;
	while (cur)
	{
		if (p.first < cur->_pair.first)
		{
			parent = cur;
			cur = cur->left;
		}
		else if (p.first > cur->_pair.first)
		{
			parent = cur;
			cur = cur->right;
		}
		else
		{
			return;
		}
	}
	cur = new Node(p);
	if (p.first < parent->_pair.first)
	{
		parent->left = cur;
		cur->parent = parent;
	}
	else
	{
		parent->right = cur;
		cur->parent = parent;
	}

那么第二部分的内容就是检查是否出现连续的红色节点，那么由于新插入的节点规定为红色，所以这里我们就得检查父节点是否为红色，由上文的原理，我们知道，那么这里调整可能导致沿途的祖父节点与祖父节点的父节点出现颜色冲突，所以这里我们就得准备一个while循环的逻辑，然后定义一个cur指针，指向当前为新插入的节点，以及parent指针，指向其父节点，那么循环的退出条件就是一直调整到整棵树的根节点，或者父节点本身为黑色，就可以退出循环了

那么循环内部，就要判断此时的情况是对应着这三种模型的哪一种，也就是叔叔节点存在且为红还是叔叔节点存在且为黑，还是叔叔节点不存在

其中如果是叔叔节点存在且为黑的话，我们还要在对旋转进行一个判断，也就是单旋还是双旋，那么这个判断就根据父节点与祖父节点之间的方向，以及父节点与父节点同为红节点的孩子节点的方向，来共同决定是单旋以及双旋，之前AVL树是借助平衡因子来判断，那么这里则是借助方向，来判断是LL型还是LR型

而至于旋转的函数，那么我在上一篇博客AVL树中详细讲过，所以这里我就不在过多的赘述，那么这里红黑树的单旋以及双旋函数，和AVL树的旋转函数是几乎一样，只需要删除平衡因子的更新逻辑即可，那么对旋转函数的实现有疑惑的，可以看我上一期AVL树的博客

而如果是叔叔节点存在且为红，那么这里我就需要变色，那么变色完之后，我们还得将cur指针移到祖父节点，将parent指针指向祖父节点的父节点，因为变色是将祖父节点变成红色，父节点和兄弟节点变成黑色，所以需要判断祖父节点和其父节点是否会出现颜色的冲突可能

最后退出循环，我们再把整棵树的根节点设置为黑，因为我们可能会调整到整棵树的根节点，那么此时如果父节点为红，且叔叔节点存在且为红，会将整棵树的根节点变成红色，所以在推出循环的时候，将整颗树的根节点设置为黑

cpp 复制代码

	void insert(const std::pair<key,val>& p)
	{
		if (root == nullptr)
		{
			root = new Node(p);
			root->_col = BLACK;
			return;
		}
		Node* cur = root;
		Node* parent = nullptr;
		while (cur)
		{
			if (p.first < cur->_pair.first)
			{
				parent = cur;
				cur = cur->left;
			}
			else if (p.first > cur->_pair.first)
			{
				parent = cur;
				cur = cur->right;
			}
			else
			{
				return;
			}
		}
		cur = new Node(p);
		if (p.first < parent->_pair.first)
		{
			parent->left = cur;
			cur->parent = parent;
		}
		else
		{
			parent->right = cur;
			cur->parent = parent;
		}
		while(parent && parent->_col == RED)
		{
			Node* grandfather = parent->parent;
			if (parent == grandfather->left)
			{
				Node* uncle = grandfather->right;
					if (uncle && uncle->_col == RED)
					{
						parent->_col = BLACK;
						uncle->_col = BLACK;
						grandfather->_col = RED;

						cur = grandfather;
						parent = cur->parent;
					}
					else
					{
						if (cur == parent->left)
						{
							RotationR(grandfather);
							
							grandfather->_col = RED;
							parent->_col = BLACK;
							break;
						}
						else
						{
							RotationL(parent);
							RotationR(grandfather);

							grandfather->_col = RED;
							cur->_col = BLACK;
							break;
						}
					}
			}
			else
			{
				Node* uncle = grandfather->left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->parent;
				}
				else
				{
					if (cur == parent->right)
					{
						RotationL(grandfather);

						grandfather->_col = RED;
						parent->_col = BLACK;
						break;
					}
					else
					{
						RotationR(parent);
						RotationL(grandfather);

						grandfather->_col = RED;
						cur->_col = BLACK;
						break;
					}
				}
			}
	}
		root->_col = BLACK;
	}

判断红黑树是否平衡Isbalanced函数

那么判断一个红黑树是否平衡，那么就是得确认该红黑树的最长路径是否会超过最短路径的2倍，那么我们不可能遍历每一个局部的子树，然后计算出每一个路径的长度，然后得到最长以及最短路径，最后判断最长路径是否会超过最短路径的2倍

而这里我则是定义了一个辅助函数,根据上文，我们知道我们不需要显示的计算出最长路径以及最短路径，因为我们有前面5点性质的约束，只要保证不会出现连续的红节点，且根节点到每一个NIL节点的路径的黑色节点个数相等，那么自然这棵树的最长路径不会超过最短路径的2倍

所以我首先判断以当前节点作为根节点的局部的二叉搜索树，那么根节点到达底部的所有NIL节点的路径的黑色节点个数是否相等，那么这里我们实际上没必要计算出每一条路径的黑色节点个数，而是先计算出一个路径的黑色节点的个数，作为基准值，然后再依次计算出其他所有路径的黑色节点个数，如果某一个路径的黑色节点个数与基准值不相等，就不用再计算其他路径的黑色节点个数，那么该局部二叉搜索树就是不平衡的，而这里的基准值，我就是选择最左侧的路径，然后再定义了一个checkBlacknum函数，那么该函数就是从根节点出发，一直递归遍历到底部的NIL节点，并且checkBlacknum维护一个num变量，来记录当前路径的黑色节点个数，如果遍历的当前节点为黑色，那么num遍历加加，然后递归遍历左右子树，到达底部的空节点的时候，就和基准值比较

cpp 复制代码

bool checkBlacknum(Node* parent, int num, int basic)
{
	if (parent == nullptr)
	{
		if (num != basic)
		{
			return false;
		}
		return true;
	}
	if (parent->_col == BLACK)
	{
		num++;
	}
	return checkBlacknum(parent->left, num, basic) && checkBlacknum(parent->right, num, basic);
}

而这里判断是否出现连续的红色节点，则是定义一个checkRed哈数，那么其中递归往下遍历的途中会与上层的父节点比较，借助parent指针，看是否出现连续的红节点，如果当前节点和父节点都不是红色，然后递归遍历左右子树，直到到达NIL节点，如果都是红色，那么直接往上回溯返回false

cpp 复制代码

bool checkRed(Node* parent)
{
	if (parent == nullptr)
	{
		return true;
	}
	if (parent == root && parent->_col != BLACK)
	{
		return false;
	}
	if (parent->_col == RED && parent->parent->_col == RED)
	{
		return false;
	}
	return checkRed(parent->left) && checkRed(parent->right);
}

最后的Isbalanced函数的大逻辑，就是检查当前根节点是否为整棵树的根节点，如果是，就需要额外判断其颜色是否为黑，那么在依次判断性质4和性质3，也就是调用checkBlacknum函数和checkRed函数，如果函数的返回值为false，直接返回，如果两个函数的返回值为true，就继续递归的判断左右子树的平衡

cpp 复制代码

	bool isbalanced(Node* parent)
	{
		if (parent == nullptr)
		{
			return true;
		 }
		if (parent == root && parent->_col != BLACK)
		{
			return false;
		}
		int basic = 0;
		Node* cur = parent;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				basic++;
			}
			cur = cur->left;
		}
		if (checkBlacknum(parent, 0, basic) == false)
		{
			return false;
		}
		if (checkRed(parent) == false)
		{
			return false;
		}
		return isbalanced(parent->left) && isbalanced(parent->right);
	}

拷贝构造函数

那么这里拷贝构造函数的逻辑，我则是定义了一个copy函数来实现，接收一个指向当前红黑树的根节点指针parent1的引用和被拷贝对象的红黑树的根节点指针parent2的引用，那么采取前序遍历，那么如果当前遍历的parent2指针为nullptr，那么就直接设置parent1为nullptr

非空，就是开辟节点，由于这里是引用，这里的引用就是父节点的左指针或者右指针的别名，所以我们直接开辟节点即可，无序处理连接关系，然后将parent2指向的节点的颜色标记拷贝到当前创建好的新节点，然后再递归遍历左子树和右子树

那么左子树和右子树遍历完，回溯到当前节点时，意味着左右子树的节点都已经创建完，那么就让当前节点的左右孩子的parent指针指向该节点，但要注意左右子树可能为空，所以需要判断一下

cpp 复制代码

void copy(Node*& parent1, Node* const& parent2)
{
	if (parent2 == nullptr)
	{
		parent1 = nullptr;
		return;
	}
	parent1 = new Node(parent2->_pair);
	parent1->_col = parent2->_col;
	copy(parent1->left, parent2->left);
	copy(parent1->right, parent2->right);
	if (parent1->left)
	{
		parent1->left->parent = parent1;
	}
	if (parent1->right)
	{
		parent1->right->parent = parent1;
	}
}
RBTree(const std::pair<key, val>& p)
	:root(new Node(p))
{
	root->_col = BLACK;
}

析构函数

那么这里由于红黑树每一个节点都是动态申请的，所以我们需要释放每一个动态申请的节点，那么这里我将红黑树每一个节点的释放逻辑定义到了destroyTree函数中，那么其采取的就是后序遍历，那么先释放左子树，再释放右子树，最后释放根节点

cpp 复制代码

void destroyTree(Node* parent)
{
	if (parent == nullptr)
	{
		return;
	}
	destroyTree(parent->left);
	destroyTree(parent->right);
	delete parent;
}
~RBTree()
{
	destroyTree(root);
}

源码

RBTree.h:

cpp 复制代码

#pragma once
#include<utility>
namespace wz
{
	enum  color
	{
		BLACK,
		RED
	};
	template<typename key,typename val>
	class RBTreeNode
	{
	public:
		RBTreeNode<key, val>* left;
		RBTreeNode<key, val>* right;
		RBTreeNode<key, val>* parent;
		std::pair<key, val> _pair;
		color _col;
		RBTreeNode()
			:_col(RED)
			, left(nullptr)
			, right(nullptr)
			, parent(nullptr)
			,_pair(std::make_pair(key(),val()))
		{

		}
		RBTreeNode(const std::pair<key,val>& p)
			:_col(RED)
			, left(nullptr)
			, right(nullptr)
			, parent(nullptr)
			,_pair(p)
		{

		}
	};
	template<typename key,typename val>
	class RBTree
	{
	private:
		typedef RBTreeNode<key, val> Node;
		Node* root;
		void RotationL(Node* parent)
		{
			Node* cur = parent->right;
			Node* curleft = cur->left;
			Node* pparent = parent->parent;

			parent->parent = cur;
			parent->right = curleft;

			cur->parent = pparent;
			cur->left = parent;
			if (curleft)
				curleft->parent = parent;
			if (pparent)
			{
				if (pparent->left == parent)
				{
					pparent->left = cur;
				}
				else
				{
					pparent->right = cur;
				}
			}
			else
			{
				root = cur;
			}
		}
		void RotationR(Node* parent)
		{
			Node* cur = parent->left;
			Node* curright = cur->right;
			Node* pparent = parent->parent;

			parent->parent = cur;
			parent->left = curright;
			cur->right = parent;

			if (curright)
				curright->parent = parent;
			cur->parent = pparent;
			if (pparent)
			{
				if (pparent->left == parent)
				{
					pparent->left = cur;
				}
				else
				{
					pparent->right = cur;
				}
			}
			else
			{
				root = cur;
			}
			
		}
		void copy(Node*& parent1, Node* const& parent2)
		{
			if (parent2 == nullptr)
			{
				parent1 = nullptr;
				return;
			}
			parent1 = new Node(parent2->_pair);
			parent1->_col = parent2->_col;
			copy(parent1->left, parent2->left);
			copy(parent1->right, parent2->right);
			if (parent1->left)
			{
				parent1->left->parent = parent1;
			}
			if (parent1->right)
			{
				parent1->right->parent = parent1;
			}
		}
		void destroyTree(Node* parent)
		{
			if (parent == nullptr)
			{
				return;
			}
			destroyTree(parent->left);
			destroyTree(parent->right);
			delete parent;
		}
		bool checkBlacknum(Node* parent, int num, int basic)
		{
			if (parent == nullptr)
			{
				if (num != basic)
				{
					return false;
				}
				return true;
			}
			if (parent->_col == BLACK)
			{
				num++;
			}
			return checkBlacknum(parent->left, num, basic) && checkBlacknum(parent->right, num, basic);
		}
		bool checkRed(Node* parent)
		{
			if (parent == nullptr)
			{
				return true;
			}
			if (parent == root && parent->_col != BLACK)
			{
				return false;
			}
			if (parent->_col == RED && parent->parent->_col == RED)
			{
				return false;
			}
			return checkRed(parent->left) && checkRed(parent->right);
		}
		bool isbalanced(Node* parent)
		{
			if (parent == nullptr)
			{
				return true;
			 }
			if (parent == root && parent->_col != BLACK)
			{
				return false;
			}
			int basic = 0;
			Node* cur = parent;
			while (cur)
			{
				if (cur->_col == BLACK)
				{
					basic++;
				}
				cur = cur->left;
			}
			if (checkBlacknum(parent, 0, basic) == false)
			{
				return false;
			}
			if (checkRed(parent) == false)
			{
				return false;
			}
			return isbalanced(parent->left) && isbalanced(parent->right);
		}
	public:
		RBTree()
			:root(nullptr)
		{

		}
		RBTree(const std::pair<key, val>& p)
			:root(new Node(p))
		{
			root->_col = BLACK;
		}
		RBTree(const RBTree<key, val>& p)
		{
			copy(root, p.root);
		}
		~RBTree()
		{
			destroyTree(root);
		}
		void insert(const std::pair<key,val>& p)
		{
			if (root == nullptr)
			{
				root = new Node(p);
				root->_col = BLACK;
				return;
			}
			Node* cur = root;
			Node* parent = nullptr;
			while (cur)
			{
				if (p.first < cur->_pair.first)
				{
					parent = cur;
					cur = cur->left;
				}
				else if (p.first > cur->_pair.first)
				{
					parent = cur;
					cur = cur->right;
				}
				else
				{
					return;
				}
			}
			cur = new Node(p);
			if (p.first < parent->_pair.first)
			{
				parent->left = cur;
				cur->parent = parent;
			}
			else
			{
				parent->right = cur;
				cur->parent = parent;
			}
			while(parent && parent->_col == RED)
			{
				Node* grandfather = parent->parent;
				if (parent == grandfather->left)
				{
					Node* uncle = grandfather->right;
						if (uncle && uncle->_col == RED)
						{
							parent->_col = BLACK;
							uncle->_col = BLACK;
							grandfather->_col = RED;

							cur = grandfather;
							parent = cur->parent;
						}
						else
						{
							if (cur == parent->left)
							{
								RotationR(grandfather);
								
								grandfather->_col = RED;
								parent->_col = BLACK;
								break;
							}
							else
							{
								RotationL(parent);
								RotationR(grandfather);

								grandfather->_col = RED;
								cur->_col = BLACK;
								break;
							}
						}
				}
				else
				{
					Node* uncle = grandfather->left;
					if (uncle && uncle->_col == RED)
					{
						parent->_col = BLACK;
						uncle->_col = BLACK;
						grandfather->_col = RED;

						cur = grandfather;
						parent = cur->parent;
					}
					else
					{
						if (cur == parent->right)
						{
							RotationL(grandfather);

							grandfather->_col = RED;
							parent->_col = BLACK;
							break;
						}
						else
						{
							RotationR(parent);
							RotationL(grandfather);

							grandfather->_col = RED;
							cur->_col = BLACK;
							break;
						}
					}
				}
		}
			root->_col = BLACK;
		}
		bool Isbalanced()
		{
			return isbalanced(root);
		}
	};
}

main.cpp

cpp 复制代码

#include <iostream>
#include <vector>
#include <cassert>
#include"RBTree.h"
#include<string>
#include<cstdlib>
using namespace std;

// 测试函数
void testRBTree()
{
   std:: cout << "===== start RBtTree tests=====" << std::endl;

    // 测试1：创建空树
    {
        wz::RBTree<int, string> tree;
        assert(tree.Isbalanced() == true);
        std::cout << "test1 pass!" << std::endl;
    }

    // 测试2：插入单个节点
    {
        wz::RBTree<int, string> tree;
        tree.insert(std::make_pair(10, "Ten"));
        assert(tree.Isbalanced() == true);
        std::cout << "test2 pass!" << std::endl;
    }

    // 测试3：插入多个节点（升序）
    {
        wz::RBTree<int, string> tree;
        vector<int> keys = { 10, 20, 30, 40, 50, 60, 70 };

        for (int key : keys) {
            tree.insert(std::make_pair(key, to_string(key)));
            assert(tree.Isbalanced() == true);
        }

        std::cout << "test3 pass!" << std::endl;
    }

    // 测试4：插入多个节点（降序）
    {
        wz::RBTree<int, string> tree;
        vector<int> keys = { 70, 60, 50, 40, 30, 20, 10 };

        for (int key : keys) {
            tree.insert(std::make_pair(key, to_string(key)));
            assert(tree.Isbalanced() == true);
        }

        std::cout << "test4 pass!" << std::endl;
    }

    // 测试5：插入多个节点（随机顺序）
    {
        wz::RBTree<int, string> tree;
        vector<int> keys = { 30, 50, 20, 10, 40, 70, 60 };

        for (int key : keys) {
            tree.insert(std::make_pair(key, to_string(key)));
            assert(tree.Isbalanced() == true);
        }

        std::cout << "test5 pass" << std::endl;
    }

    // 测试6：插入重复键
    {
        wz::RBTree<int, string> tree;
        tree.insert(std::make_pair(10, "Ten" ));
        tree.insert(std::make_pair(20, "Twenty" ));
        tree.insert(std::make_pair(10, "Ten Again" )); // 应被忽略

        assert(tree.Isbalanced() == true);
        std::cout << "test6 pass!" << std::endl;
    }

    // 测试7：大量随机数据
    {
        wz::RBTree<int, string> tree;
        const int N = 1000;

        // 插入1000个随机键
        for (int i = 0; i < N; i++) {
            int key = rand() % 10000;
            tree.insert(std::make_pair( key, to_string(key) ));

            // 定期检查平衡性
            if (i % 100 == 0) {
                assert(tree.Isbalanced() == true);
            }
        }

        // 最终平衡检查
        assert(tree.Isbalanced() == true);
        std::cout << "test7 pass!" << std::endl;
    }

    // 测试8：拷贝构造函数
    {
        wz::RBTree<int, string> tree1;
        tree1.insert(std::make_pair( 30, "Thirty" ));
        tree1.insert(std::make_pair(20, "Twenty" ));
        tree1.insert(std::make_pair(40, "Forty" ));

        wz::RBTree<int, string> tree2(tree1);
        assert(tree2.Isbalanced() == true);
        std::cout << "test8 pass!" << std::endl;
    }

    // 测试9：析构函数
    {
        wz::RBTree<int, string>* tree = new wz::RBTree<int, string>();
        tree->insert(std::make_pair(10, "Ten" ));
        tree->insert(std::make_pair(20, "Twenty" ));
        delete tree; // 应正确释放内存
        std::cout << "test9 pass!" << std::endl;
    }

    std::cout << "===== All tests pass!=====" << std::endl;
}

int main()
{
    testRBTree();
    return 0;
}

运行截图：

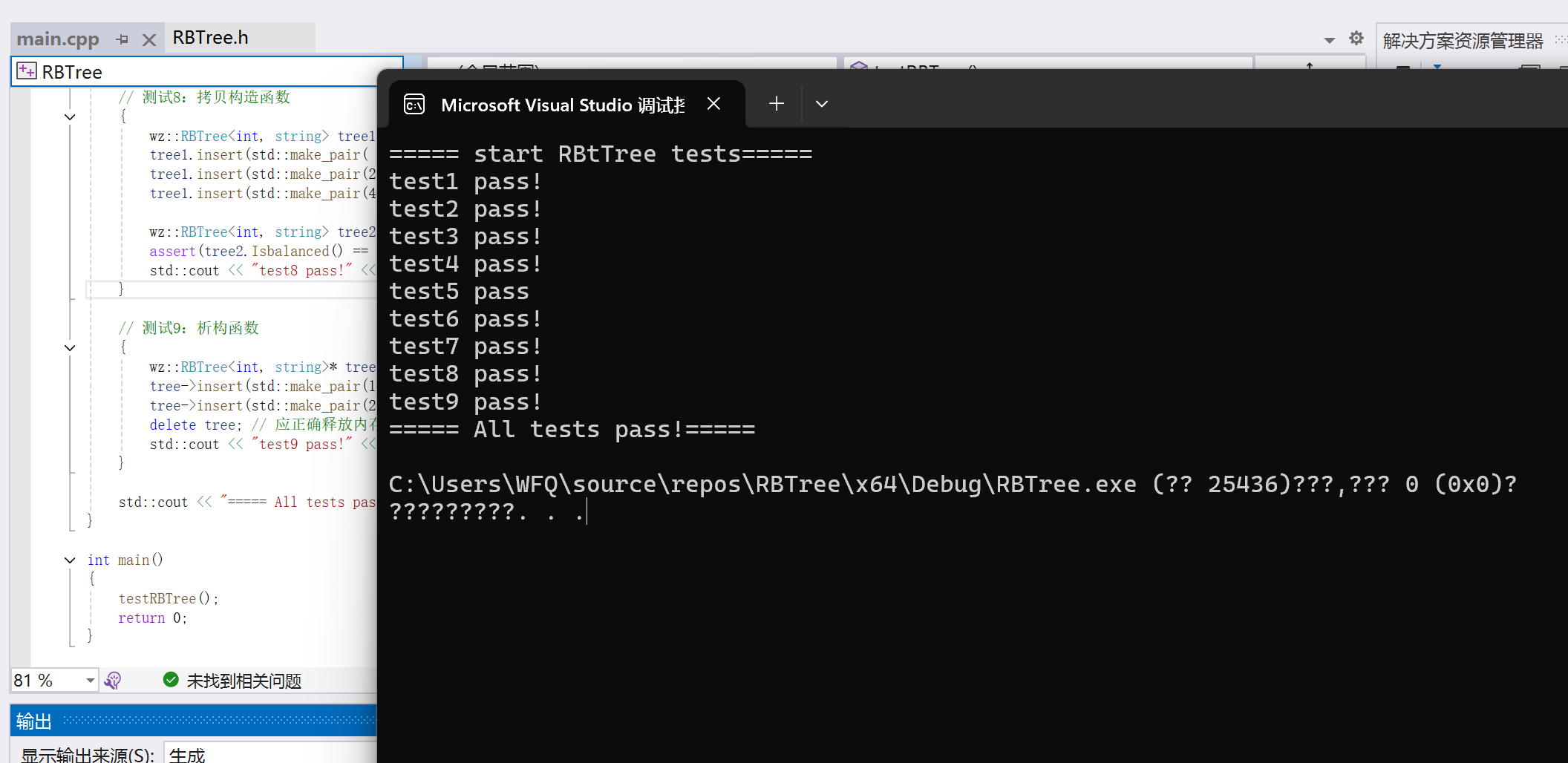
结语

那么这就是本篇文章关于红黑树的讲解的全部内容，带你从原理和实现两个维度理解红黑树，下来也建议读者能够自己去动手实现一下红黑树，加强对于红黑树的理解，那么下一期我将更新map和set，那么我会持续更新，希望你能够多多关注，如果本文对你有帮帮组，还请三连加关注，你的支持就是我创作的最大动力！