【1】引言
前序已经学习了使用Numpy和PyTorch模块绘制正态分布函数图的基本技巧,掌握了
p ( x ) = 1 2 π σ 2 e x p ( − 1 2 σ 2 ( x − μ ) 2 ) p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2) p(x)=2πσ2 1exp(−2σ21(x−μ)2)
在PyTorch里面绘制图像的基本技巧。
今天更进一步,使用torch.normal()函数直接绘制正态分布函数图。
【2】torch.normal()函数
【2.1】生成随机数
torch.normal()函数可以直接绘制正态分布函数图。
这个函数的作用是生成符合正态分布的随机数,比如:
python
# 引入模块
import torch
# 使用torch.normal()函数生成随机数
x=torch.normal(0,1,(2,3))
print(x)
a=len(x)
print('a=',a)这个代码运行会生成2行3列的满足均值为0、标准差为1的正态分布随机数。
【2.2】对随机数绘图
torch.normal()函数可以直接获得正态分布随机数,那数据就可以画出图像。
这个图像的最佳画法就是使用hist()函数来绘制概率分布图,随机数如何分布的情况一目了然。
为了做对比,我们也可以自己按照上述正态分布函数式来自定义图像。
这里给出代码:
python
import torch
import matplotlib.pyplot as plt
import numpy as np
# 生成不同样本量的数据
sample_sizes = [100, 1000, 10000] # 三种样本量
# 生成x轴数据(用于理论曲线)
x_range = np.arange(-5, 5,0.01)
datasets = [torch.normal(0, 1, (size,)).numpy() for size in sample_sizes]
# 定义正态分布概率密度函数(理论曲线)
def normal_pdf(x, mean=0, std=1):
return (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mean) / std) ** 2)
# 计算理论曲线值
y_theoretical = normal_pdf(x_range)
# 创建画布和子图
fig, ax = plt.subplots(1, 3)
for i in range(3):
ax[i].hist(datasets[i],bins=int(sample_sizes[i]*0.3), density=True, alpha=0.5, color='skyblue', edgecolor='black')
# 叠加理论正态分布曲线
ax[i].plot(x_range, y_theoretical, 'r-', linewidth=2, label='理论分布')
print(len(datasets[i]))
if i == 0: # 仅第一个子图显示y轴标签(避免重复)
ax[i].set_ylabel('torch.normal', fontsize=12)
if i == 1: # 仅第二个子图显示x轴标签(避免重复)
ax[1].set_xlabel('x', fontsize=12)
plt.show()代码给出了三个数量级的随机数概率分布直方图,第一个有100个数据,第二个有1000个数据,第三个有10000个数据。数据越多,理论上正态分布的效果越明显,实际的图像效果为:
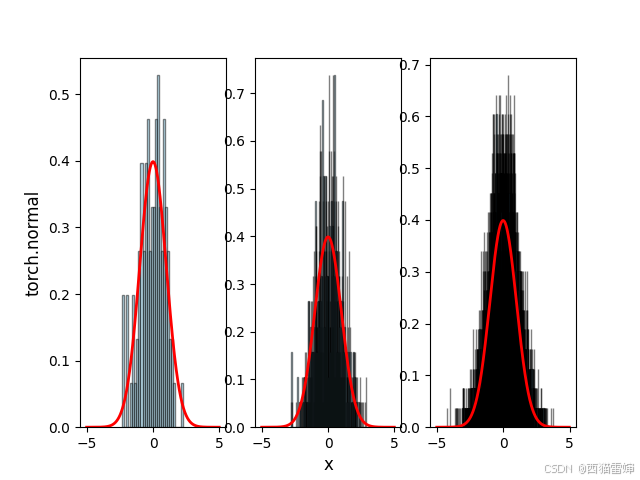
虽然图像在高度上发生了变化,但显然数据越多,直方图和曲线图拟合得更好。
【3】细节
需要注意的是,图像越来越黑,是因为hist()函数绘制了很多边框,边框的颜色edgecolor是黑色的。bins=int(sample_sizes[i]*0.3)表明数据越多,边框越多,所以黑色越来越多。
ax[i].hist(datasets[i],bins=int(sample_sizes[i]*0.3), density=True, alpha=0.5, color='skyblue', edgecolor='black')
如果想让图像的颜色一致,最佳办法就是统一所有的边框数量,比如限制边框数量为30,此时的图像效果为:
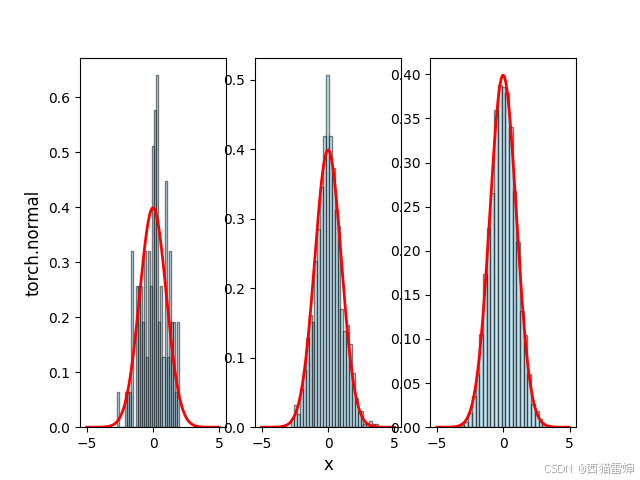
【4】说明
虽然上述代码简洁的表明了torch.normal()函数可以生成好用的正态分布随机数,但是这个代码显然写起来要比numpy模块复杂一些。
并且当前只对torch.normal(0, 1, (size,))画了图,还没有开展更复杂的图像绘制。,学习的路还长。
【5】总结
学习了使用PyTorch模块的normal()函数绘制正态分布函数图的基本方法。