从传统卷积到图卷积
在深度学习领域,卷积神经网络 (CNN) 因其在处理图像等欧几里得结构数据方面的卓越表现而广为人知。然而,现实世界中许多数据呈现出更加复杂的非欧几里得结构,如社交网络、分子结构和知识图谱等图结构数据。传统的 CNN 难以直接处理这类数据,因为图中的节点没有固定的顺序和位置,也没有规则的邻域结构。
图卷积网络 (Graph Convolutional Network, GCN) 正是为解决这一挑战而提出的。作为一种专门设计用于处理图结构数据的神经网络,GCN 能够有效捕捉图中节点的邻域信息,并生成节点的特征表示,为后续的节点分类、链接预测等任务奠定基础。
GCN 的基本原理与数学基础
图的表示与基本概念
在深入 GCN 之前,我们需要先了解图的基本表示方法。一个无向无权图 G 可以表示为 G=(V,E),其中 V 是节点集合,E 是边集合。在数学上,图通常可以通过以下两种方式表示:
- 邻接矩阵 (Adjacency Matrix): 一个 N×N 的矩阵 A,其中 A [i][j] = 1 表示节点 i 和节点 j 之间有边相连,否则为 0。
- 特征矩阵 (Feature Matrix): 一个 N×F 的矩阵 X,其中 X [i] 表示节点 i 的 F 维特征向量。
此外,还有一个重要的概念是度矩阵 (Degree Matrix) D,它是一个对角矩阵,其中 D [i][i] 等于节点 i 的度数 (即与节点 i 相连的边的数量)。
GCN 的核心思想
GCN 的核心思想是将卷积操作从传统的欧几里得空间扩展到图结构上。与 CNN 类似,GCN 通过聚合节点及其邻域的信息来更新节点的特征表示。然而,由于图结构的不规则性,GCN 需要一种不同的方式来定义 "卷积" 操作。
GCN 的关键创新在于设计了一种能够在图结构上进行信息传播的机制,使得每个节点的新特征表示不仅考虑自身的特征,还考虑其邻居节点的特征。这种机制允许 GCN 在保持参数共享的同时,有效捕捉图的局部结构信息。
GCN 的数学推导
GCN 的数学推导涉及图信号处理和谱图理论的一些概念。在这里,我们将简要介绍其核心公式的推导过程。
首先,我们考虑在图上定义的卷积操作。在谱域中,图卷积 (就是一个滤波的过程) 可以表示为:
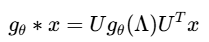
其中,U 是图拉普拉斯矩阵的特征向量矩阵,Λ 是对应的特征值对角矩阵,gθ 是滤波器参数化的函数。然而,直接计算特征分解的复杂度很高,因此需要寻找一种近似方法。
通过使用切比雪夫多项式近似,可以将图卷积转换为空间域上的局部操作。进一步简化后,我们得到了 Kipf 和 Welling 在 2017 年提出的 GCN 层的传播规则(本质上就是PageRank算法:PageRank算法介绍):

这个公式的核心操作是对邻接矩阵进行对称归一化,然后与特征矩阵和权重矩阵相乘,最后应用激活函数。这一过程可以看作是对每个节点的特征及其邻居特征进行加权平均,并通过可学习的权重矩阵进行特征变换。
GCN 的层叠结构
GCN 通常由多层堆叠而成,每一层都应用上述传播规则。每增加一层,节点的特征表示就会整合更远距离的邻居信息。例如:
- 第一层 GCN 层:直接邻居的信息
- 第二层 GCN 层:邻居的邻居的信息 (即两跳范围内的信息)
- 依此类推
python
+-----------+
| 输入图数据 |
+-----------+
|
v
+-----------+
| Convolution Layer 1 |
+-----------+
|
v
+-----------+
| ReLU |
+-----------+
|
v
+-----------+
| Convolution Layer 2 |
+-----------+
|
v
+-----------+
| ReLU |
+-----------+
|
v
+-----------+
| 输出结果 |
+-----------+然而,实践表明,超过两层的 GCN 可能会导致过平滑问题 (over-smoothing),即所有节点的特征表示变得相似,因此通常使用 2-3 层的 GCN 架构。
GCN 的 Python 实现
实现思路与准备工作
根据上述原理,我们将使用 NumPy 库实现一个简单的 GCN。为了保持代码的简洁和可读性,我们将实现一个两层的 GCN,并包含以下主要组件:
- 图结构的表示 (邻接矩阵)
- 节点特征的表示 (特征矩阵)
- 对称归一化操作
- 权重矩阵的初始化
- 前向传播计算
代码实现
python
import numpy as np
class GCN:
def __init__(self, input_dim, hidden_dim, output_dim, activation=np.tanh):
# 初始化权重矩阵
self.W1 = np.random.randn(input_dim, hidden_dim)
self.W2 = np.random.randn(hidden_dim, output_dim)
self.activation = activation
def normalize_adjacency(self, A):
# 添加自环
A_hat = A + np.eye(A.shape[0])
# 计算度矩阵
D_hat = np.sum(A_hat, axis=0)
D_hat_inv_sqrt = np.diag(1.0 / np.sqrt(D_hat))
# 对称归一化
return D_hat_inv_sqrt @ A_hat @ D_hat_inv_sqrt
def forward(self, X, A):
# 归一化邻接矩阵
A_normalized = self.normalize_adjacency(A)
# 第一层GCN
H1 = self.activation(A_normalized @ X @ self.W1)
# 第二层GCN
H2 = A_normalized @ H1 @ self.W2
return H2
# 示例用法
if __name__ == "__main__":
# 定义一个简单的图结构(邻接矩阵)
A = np.array([
[0, 1, 0, 0],
[1, 0, 1, 1],
[0, 1, 0, 0],
[0, 1, 0, 0]
], dtype=np.float32)
# 节点特征矩阵(4个节点,每个节点有3维特征)
X = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]
], dtype=np.float32)
# 创建GCN模型(输入维度3,隐藏层维度4,输出维度2)
gcn = GCN(input_dim=3, hidden_dim=4, output_dim=2)
# 前向传播
output = gcn.forward(X, A)
print("输出特征矩阵:")
print(output)代码解释
在示例中,我们定义了一个包含 4 个节点的简单图结构,并为每个节点提供了 3 维特征。通过创建一个两层的 GCN 模型 (隐藏层维度为 4,输出维度为 2),我们可以得到每个节点的 2 维特征表示。
该示例展示了 GCN 如何将输入特征矩阵和邻接矩阵转换为节点的低维表示,这可以用于后续的分类或聚类任务。即使没有经过训练,这个简单的 GCN 模型也能捕捉到图结构中的一些信息,如节点之间的连接模式。
-
初始化方法 (init):
- 初始化两个权重矩阵 W1 和 W2,分别用于第一层和第二层 GCN
- 激活函数默认为双曲正切函数 tanh,可以根据需要修改
-
normalize_adjacency 方法:
- 添加自环:通过将邻接矩阵 A 与单位矩阵相加,确保每个节点都包含自身的信息
- 计算度矩阵:通过对 A_hat 的每一行求和得到度矩阵 D_hat
- 对称归一化:计算 D_hat 的逆平方根矩阵,并与 A_hat 进行矩阵乘法,得到归一化后的邻接矩阵
-
forward 方法:
- 对输入的邻接矩阵进行归一化处理
- 第一层 GCN:将归一化后的邻接矩阵与输入特征矩阵和权重矩阵 W1 相乘,然后应用激活函数
- 第二层 GCN:将第一层的输出与归一化后的邻接矩阵和权重矩阵 W2 相乘,不应用激活函数 (假设用于分类任务)
- 返回最终的节点特征表示