算法入门：专题攻克主题一---双指针（2）快乐数 呈最多水的容器

🎬 胖咕噜的稞达鸭 ：个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》《算法入门》

⛺️技术的杠杆，撬动整个世界!

---

快乐数

快乐数leetcode题目

题目解析：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，假设对于正整数19，个位数是9，十位数是1，每个位置的平方和为1*1+9*9=82；然后一直重复，8*8+2*2=68；6*6+8*8=100；1*1+0*0+0*0=1.最后的结果变为1，所以这个数字19就是快乐数。

无限循环的情况：假设对于数字2，2* 2=4，4* 4=16， 1* 1+ 6 * 6=37，3* 3+7* 7=58；5* 5+8* 8=89；8 *8+9* 9=145；1* 1+4* 4+5* 5=42；4* 4+2* 2=20；2 *2+0 *0=4；会一直循环但是永远都不可能成为1.

算法原理：

其实这两种情况可以近似看成同一种情况：都是来判断是否有环，快乐数的环中所有数字都是1，但是无限循环的环中是不相等的数字。
判断链表是否有环：用快慢双指针的解法来操作
1.定义快慢指针；
2.让满指针每次向后移动一步，快指针每次向后移动一步；
3.判断相遇的时候的值即可。

1. 数字跟指针如何关联？

在链表中我们可以用Node*来定义快慢指针，但是这里是数字，数字跟指针该如何关联？

那干脆将数字定义为指针就可以解决我们的问题了，比如正整数2，刚开始slow=2，slow走一步，变成slow=4，fast=2，fast走两步，fast=16。最后slow指向位置，判断

2. 证明一下"重复这个数字直到它变为1，也可能是无限循环变不到1"这句话，有没有可能不会进入到环中？

这里会用到鸽巢原理，鸽巢原理（抽屉原理）有n个巢，有n+1个鸽子至少有一个巢穴，里面的鸽子数量大于等于1.

在这道题的数字大小限制1<=n<=2的31次方-1，近似于2.1*10的9次方，这里我们扩大范围，直接给十个9，9999999999这个数字，一定是大于2.1*10的9次方，9999999999将该数替换为它每个位置上的数字的平方和，9的平方*10=810，也就是说这个大小限制一定是在1到810之内变化，这就搭建好了我们的鸽巢；

现在来找鸽子，给一个数字，让它变化811次，1到810之间有810个数字，经过811次变化，一定会循环到[1，810]之内的某个数字，一定会进入到一个环当中。

现在开始写代码：

3. 该怎么取一个正整数的每一个位置的数字的平方和？

这里我们会经常用到一个函数bitSum来进行封装，sum 赋值为0用来计算每一次的平方和，假如19这个正整数，用t表示个位十位，第一次取到个位，19%10=9，sum =0+9*9=81,取十位的数字，19/10=1，sum等于81.

上代码！

class Solution {
public:
    int bitSum(int n)//返回n这个数每一个位置的平方和
    {
        int sum=0;
        while(n)
        {
            int t=n%10;
            sum+=t*t;
            n/=10;//假设个位上的数字取完了，这一步操作去取十位的数字
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow=n,fast=bitSum(n);//bitSum(n)是第二个位置
        while(slow!=fast)//当这两个指针不相等的时候要进入循环，所以我们把最开始的fast指向第二个位置
        {
            slow=bitSum(slow);
            fast=bitSum(bitSum(fast));
        }
        return slow==1;
    }
};

呈最多水的容器

呈最多水的容器leetcode题目

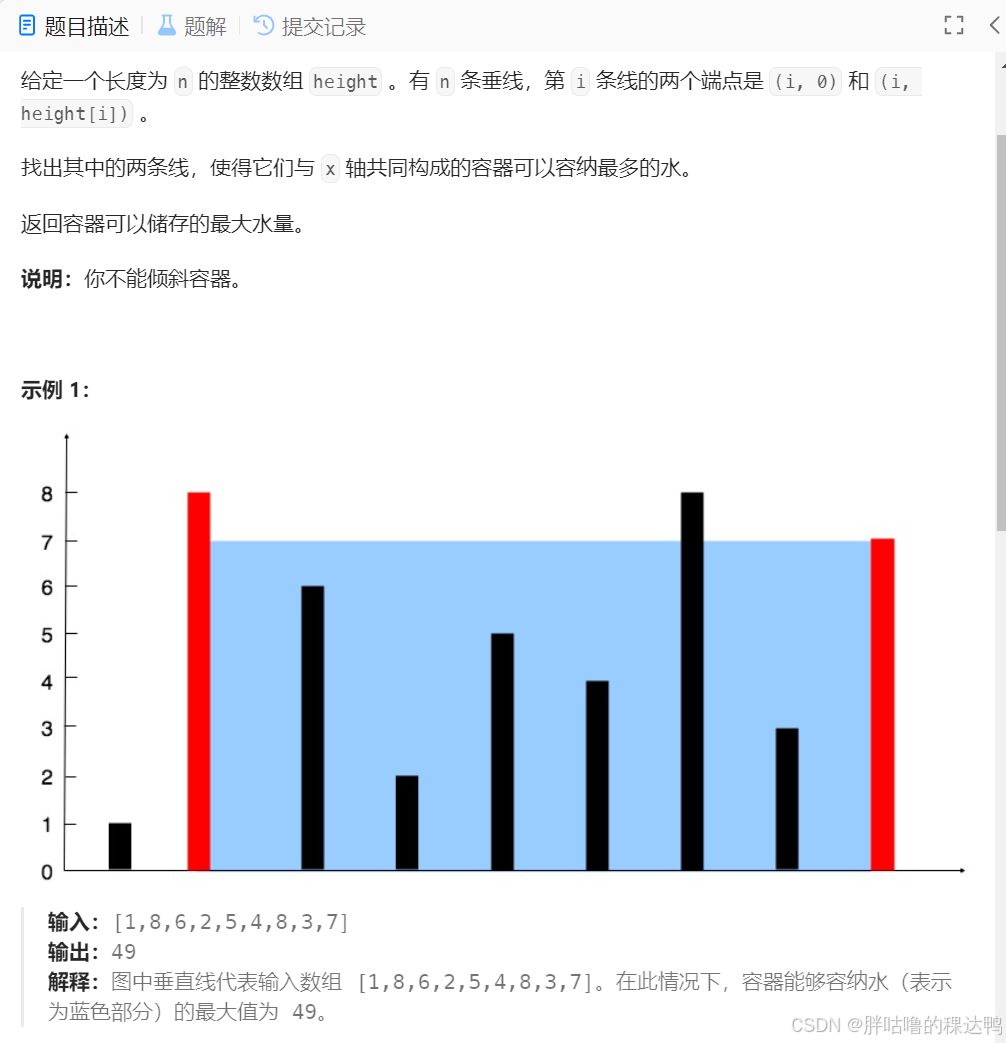
题目解析：

找到纵轴上面最高的两条线，在上文图片中，选择两条线是数组下标为1和8的两条线，这两条线用来作为容器的两边，由于木桶效应，容器可以呈多少水都是由较短的那条线决定的，较短的线在纵轴上数值为7，两条线之间的差距在横轴上数值为7，这样的组合可以盛放49单位的水，要是选择1号线和6号线，按照上面的步骤，最多可以容纳40个单位的水，所以这个容器最多可以盛放49单位的水。

算法原理：

解法一：暴力枚举

但是一定会超时；

解法二：

如果随便拿两个数，假设在[ 1,8,6,2,5,4,8,3,7]这个数组中，随意拿到的两个数字是6和4，区间为[6，2，5，4]，计算容器的体积：4*3=12；如果4向内枚举，会有两种情况，一种是碰到比4大的数字5，计算体积：高不变还是4但是宽度减小，体积一定会减小；一种遇到比4小的数字2，计算体积：高减小而且宽度也减小，体积一定会减小。有这个规律可以减少很多次枚举带来的不便。

所以我们干脆拿第一个数字和最后一个数字进行枚举，这个体积记为v1;再次拿掉第一个数字和最后一个数字当中最小的那个数字，拿掉1，向后进行遍历，再算出v2，依次计算直到拿到最中间的两个数。

利用单调性，使用双指针来解决问题，每次分别向内移动一步，直到相遇停止。

定义left指向下标为0，right指向下标为n-1；计算出v1;

比较两个指针指向的值，较小的值移动；计算出v2;每算出一个体积就更新一下最大值。

1. 该怎么拿到好多v中最大的那个呢？如果要定义一个数组收纳所有v，最后再找出最大的max[v]是否繁琐？

不用，我们这里用left指向下标为0，right指向下标为height.size()-1，用ret来接收算出的最大容器体积，每次算出的体积都要跟ret中存的最大体积进行比较，不断更新，最后留下来的就是最大体积了。

上代码！

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0,right=height.size()-1,ret=0;
        while(left<right)
        {
            int v=(right-left)*min(height[left],height[right]);
            ret=max(ret,v);
            //移动指针
            if(height[left]<height[right]) left++;
            else right--;
        }
        return ret;
    }
};