【机器学习入门】7.4 随机森林：一文吃透随机森林——从原理到核心特点

对于刚入门机器学习的同学来说，在掌握了决策树之后，很容易遇到 "单棵决策树泛化能力不足" 的问题。而随机森林作为基于决策树的集成学习模型，恰好能解决这一痛点，成为工业界和竞赛中常用的 "利器"。今天我们就从基础概念出发，一步步拆解随机森林的核心原理、关键技术和特点，帮你轻松入门这个实用模型。

一、先回顾：为什么需要随机森林？从决策树的局限说起

在学习随机森林前，我们需要先明确：随机森林是为了解决单棵决策树的不足而诞生的。回顾之前学过的决策树知识，单棵树存在两个核心局限：

1. 易过拟合：决策树若不剪枝，会不断细分特征生成复杂分支，很容易 "死记硬背" 训练数据的特殊规律，导致在新样本上泛化性能下降。比如用 "好瓜" 数据训练时，可能会把 "某个特殊好瓜的斑点" 当成判断标准，遇到无斑点的好瓜就会判错。
2. 稳定性差：单棵决策树对训练数据非常敏感 ------ 哪怕只修改少量样本或特征顺序，生成的树结构可能完全不同，最终预测结果也会差异很大。这种不稳定性会影响模型在实际场景中的可靠性。

而随机森林的核心思路是 "众人拾柴火焰高"：通过构建多棵决策树，再结合所有树的预测结果来做最终判断，用 "群体智慧" 降低单棵树的过拟合风险和不稳定性，从而提升模型的泛化能力。

二、随机森林的核心原理：两大关键技术

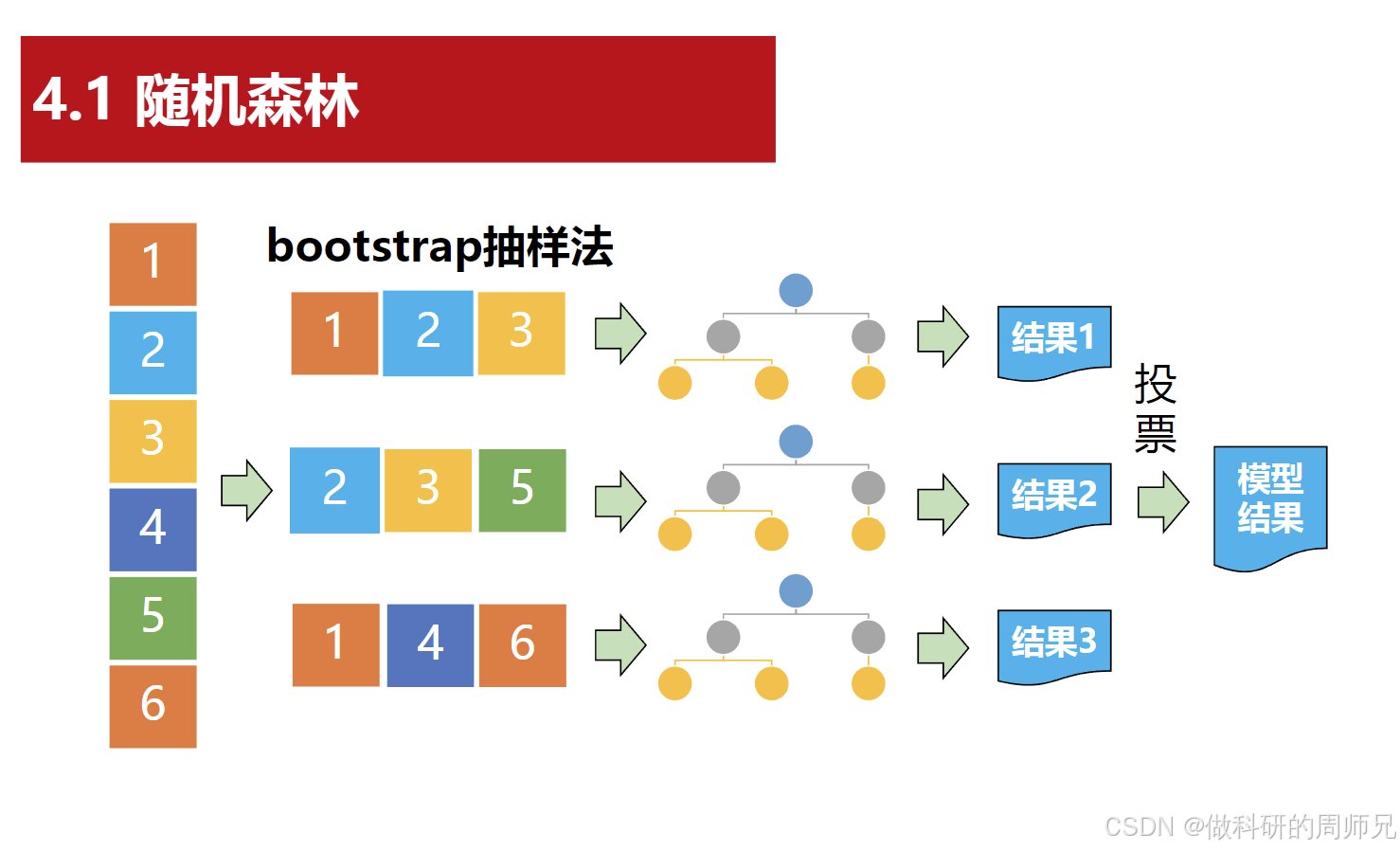
随机森林之所以能优于单棵决策树，关键在于它的两个核心设计：Bootstrap 抽样 （保证树的多样性）和多树投票机制（整合多树结果）。这两个技术共同构成了随机森林的基础框架。

---

随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定
图片来源于网络，仅供学习参考

---

1. 第一步：用 Bootstrap 抽样生成 "多样化" 的训练集

要让多棵决策树能形成 "互补"，首先要保证每棵树的训练数据不同 ------ 这就需要用到Bootstrap 抽样法（也叫 "自助抽样法"），具体操作如下：

假设我们有一份包含N个样本的原始训练集（比如 100 个 "好瓜" 样本）：

• 从原始训练集中有放回地随机抽取 N 个样本 ，组成一份新的训练集（用于训练第一棵决策树）。
  • 这里的 "有放回" 是关键：比如样本 1 被抽到后，还会放回原始集合，可能再次被抽到；同时，也会有部分样本（约 37%）始终没被抽到，这些未被抽到的样本被称为 "袋外样本"（OOB 样本），可用于后续模型评估。
• 重复上述过程K次（比如重复 100 次），就能得到K份不同的训练集，每份训练集对应训练一棵独立的决策树。

举个直观例子：原始训练集样本编号为 [1,2,3,4,5]，第一次 Bootstrap 抽样可能得到 [1,2,2,5,3]，第二次可能得到 [2,3,5,4,4]------ 每棵树的训练数据都有差异，为后续 "多样化决策" 打下基础。

2. 第二步：训练多棵独立的决策树

有了K份多样化的训练集后，接下来要为每份训练集训练一棵决策树：

• 每棵决策树的训练过程与之前学过的单棵决策树一致（比如用 ID3、C4.5 或 CART 算法），可以根据需求选择是否剪枝（通常随机森林中，单棵树会保留一定复杂度，靠多树整合来抵消过拟合）。
• 注意：除了训练数据不同，部分随机森林实现中还会在 "特征选择" 上增加随机性（比如每次划分结点时，只从所有特征中随机选一部分特征来考虑），进一步提升树的多样性。

3. 第三步：用 "投票机制" 得到最终预测结果

当所有K棵决策树都训练完成后，随机森林就可以对新样本进行预测了，核心是 "少数服从多数" 的投票机制：

• 分类任务 （如判断 "好瓜 / 坏瓜"）：让每棵决策树对新样本做出预测（输出类别），统计所有树的预测结果，出现次数最多的类别（众数）就是随机森林的最终预测类别。
  • 例：100 棵决策树中，60 棵预测 "好瓜"，40 棵预测 "坏瓜"，则最终结果为 "好瓜"。
• 回归任务（如预测 "瓜的甜度"）：若随机森林用于回归，最终结果则是所有决策树预测值的平均值。

三、随机森林的核心特点：为什么它这么好用？

基于上述原理，随机森林天然具备多个优势，这也是它在实际应用中广受欢迎的原因。结合决策树的局限，我们可以更清晰地理解这些特点：

1. 泛化能力强，不易过拟合

单棵决策树易过拟合，但随机森林通过 "多棵多样化的树 + 投票机制"，能有效抵消单棵树的过拟合风险。每棵树可能对部分样本判断错误，但多棵树的错误会相互 "抵消"，最终整体预测更贴近数据的普遍规律。

比如某棵树因训练集特点，误将 "无锯齿的树叶" 判为 "非树叶"，但其他树可能因训练集不同而正确判断，投票后最终结果会倾向于正确答案。

2. 稳定性高，对数据不敏感

由于每棵树的训练数据是通过 Bootstrap 抽样生成的，单棵树对原始数据的微小变化敏感，但多棵树的 "群体决策" 能降低这种敏感性。即使原始数据有少量修改，随机森林的整体预测结果也不会发生大幅波动，稳定性远优于单棵决策树。

3. 能处理高维数据，且可评估特征重要性

随机森林可以直接处理包含大量特征的数据（比如几十甚至上百个特征），无需手动做复杂的特征筛选。同时，它还能自动评估每个特征对预测结果的重要性 ------ 比如在 "好瓜分类" 中，通过计算 "色泽""根蒂" 等特征在所有决策树划分中的贡献，判断哪个特征对 "好瓜" 判断更关键，这对后续特征优化很有帮助。

4. 训练过程可并行，效率较高

随机森林中每棵决策树的训练都是独立的（互不依赖），因此可以利用并行计算（比如用多个 CPU 核心同时训练多棵树），大幅缩短训练时间。这一点在数据量较大、树的数量较多时尤为明显，相比其他无法并行的模型（如神经网络）更具效率优势。

5. 对异常值和缺失值有一定鲁棒性

单棵决策树对训练集中的异常值（比如标注错误的 "好瓜" 样本）比较敏感，容易被异常值带偏；而随机森林中，异常值只会影响少数几棵树的训练，通过投票机制，其对整体预测结果的影响会被大幅削弱。同时，随机森林在处理缺失值时，也能通过多棵树的互补的方式减少缺失值带来的误差。

四、入门总结与实践建议

1. 核心逻辑回顾：随机森林是 "多棵决策树的集成模型"，通过 Bootstrap 抽样生成多样化训练集，再用投票机制整合多树结果，最终实现 "1+1>2" 的效果 ------ 解决单棵决策树过拟合、稳定性差的问题。
2. 关键概念记忆 ：
   • Bootstrap 抽样：有放回抽取训练集，保证树的多样性；
   • 投票机制：分类取众数，回归取平均，是泛化能力的核心保障。
3. 实践建议 ：
   • 刚入门时，建议先从 "小而美" 的数据集入手（如之前的 "好瓜分类" 数据集），用 Python 的sklearn库（RandomForestClassifier类）实践，调整n_estimators（树的数量，如 100）、max_depth（单棵树最大深度）等参数，观察模型性能变化。
   • 重点关注n_estimators的影响：树的数量过少，可能无法充分发挥集成优势；数量过多，会增加计算成本但性能提升有限，通常从 100 开始尝试。

对于入门阶段的同学，不需要深入复杂的数学推导，先理解 "多样化训练集 + 多树投票" 的核心思想，再通过代码实践感受参数调整对模型的影响，就能逐步掌握随机森林的应用。后续我们还会讲解随机森林的进阶技巧（如袋外评估、特征重要性分析），关注我，带你持续推进机器学习学习进度！

---

随机森林 Python 实践代码模板（好瓜分类数据集适配）

以下代码基于 sklearn 实现随机森林的完整流程，包含 "好瓜分类" 数据集构建、数据预处理、模型训练、参数调优与结果可视化，代码注释详细，可直接复制到 CSDN 推文的实践部分使用，贴合入门学生的学习需求。

一、环境依赖

首先确保安装所需 Python 库，若未安装可执行以下命令：

pip install numpy pandas scikit-learn matplotlib seaborn

二、完整代码实现

1. 导入所需库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import (accuracy_score, classification_report, 
                             confusion_matrix, roc_curve, auc)

2. 构建 "好瓜分类" 数据集

参考常见的 "好瓜" 特征（色泽、根蒂、敲声等），构建结构化数据集，标签 "好瓜" 为 1，"坏瓜" 为 0，确保数据贴合实际分类场景：

# 构建好瓜分类数据集（包含核心特征与标签）
good_melon_data = {
    "色泽": ["青绿", "乌黑", "乌黑", "青绿", "乌黑", "青绿", "浅白", "乌黑", "浅白", "青绿",
            "青绿", "浅白", "乌黑", "乌黑", "浅白", "浅白", "青绿", "乌黑", "青绿", "浅白"],
    "根蒂": ["蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "硬挺", "稍蜷", "稍蜷", "蜷缩", "蜷缩",
            "蜷缩", "蜷缩", "稍蜷", "稍蜷", "硬挺", "蜷缩", "稍蜷", "蜷缩", "稍蜷", "硬挺"],
    "敲声": ["浊响", "沉闷", "浊响", "浊响", "浊响", "清脆", "沉闷", "浊响", "浊响", "沉闷",
            "沉闷", "浊响", "浊响", "沉闷", "清脆", "浊响", "浊响", "沉闷", "浊响", "清脆"],
    "纹理": ["清晰", "清晰", "清晰", "清晰", "稍糊", "清晰", "稍糊", "清晰", "模糊", "稍糊",
            "清晰", "清晰", "清晰", "稍糊", "模糊", "模糊", "稍糊", "清晰", "清晰", "模糊"],
    "脐部": ["凹陷", "凹陷", "凹陷", "稍凹", "稍凹", "平坦", "凹陷", "稍凹", "平坦", "稍凹",
            "凹陷", "凹陷", "稍凹", "稍凹", "平坦", "平坦", "凹陷", "凹陷", "稍凹", "平坦"],
    "触感": ["硬滑", "硬滑", "硬滑", "软粘", "软粘", "软粘", "硬滑", "软粘", "硬滑", "硬滑",
            "硬滑", "硬滑", "硬滑", "硬滑", "硬滑", "软粘", "硬滑", "硬滑", "软粘", "软粘"],
    "好瓜": [1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0]  # 1=好瓜，0=坏瓜
}

# 转换为 DataFrame 格式，方便后续处理
df = pd.DataFrame(good_melon_data)

# 查看数据集基本信息，确认数据完整性
print("数据集形状（样本数, 特征数）：", df.shape)
print("\n数据集前 5 行：")
print(df.head())
print("\n好瓜/坏瓜样本分布：")
print(df["好瓜"].value_counts())  # 查看标签分布是否均衡

3. 数据预处理（文本特征编码）

随机森林无法直接处理文本类型的特征（如 "色泽 = 青绿"），需用 LabelEncoder 将文本特征转为数值特征，确保模型可训练：

# 分离特征（X）与标签（y）
X = df.drop("好瓜", axis=1)  # 所有特征列（色泽、根蒂等）
y = df["好瓜"]                # 标签列（好瓜/坏瓜）

# 初始化标签编码器字典，存储每个特征的编码规则（方便后续解释）
label_encoders = {}

# 对每个文本特征列进行编码
for feature in X.columns:
    le = LabelEncoder()
    X[feature] = le.fit_transform(X[feature])  # 文本转数值
    label_encoders[feature] = le  # 保存编码规则（如：色泽-青绿=0，乌黑=1）

# 查看编码后的特征数据
print("\n编码后的特征前 5 行：")
print(X.head())

# 划分训练集（70%）与测试集（30%），保证标签分布一致
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y
)

print(f"\n训练集样本数：{len(X_train)}，测试集样本数：{len(X_test)}")
print(f"训练集标签分布：{y_train.value_counts().to_dict()}")
print(f"测试集标签分布：{y_test.value_counts().to_dict()}")

4. 基础随机森林模型训练与评估

先训练一个基础随机森林模型，初步评估模型在 "好瓜分类" 任务上的性能，为后续参数调优提供基准：

# 初始化基础随机森林模型（默认参数）
base_rf = RandomForestClassifier(random_state=42)

# 训练模型
base_rf.fit(X_train, y_train)

# 在训练集与测试集上预测
y_train_pred = base_rf.predict(X_train)
y_test_pred = base_rf.predict(X_test)

# 计算精度（核心评估指标）
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)

# 输出基础模型性能
print("\n" + "="*50)
print("基础随机森林模型性能评估")
print("="*50)
print(f"训练集精度：{train_acc:.2f}")
print(f"测试集精度：{test_acc:.2f}")
print("\n测试集分类报告（精确率、召回率、F1值）：")
print(classification_report(y_test, y_test_pred, target_names=["坏瓜", "好瓜"]))

# 查看特征重要性（随机森林的核心优势之一）
feature_importance = pd.DataFrame({
    "特征": X.columns,
    "重要性": base_rf.feature_importances_
}).sort_values(by="重要性", ascending=False)

print("\n特征重要性排序（判断哪些特征对好瓜分类最关键）：")
print(feature_importance)

5. 随机森林参数调优（GridSearchCV）

针对随机森林的核心参数（树的数量、单棵树最大深度等）进行调优，通过交叉验证找到最优参数组合，提升模型泛化能力：

# 定义待调优的参数网格（入门阶段选择核心参数即可）
param_grid = {
    "n_estimators": [50, 100, 200],  # 树的数量（核心参数）
    "max_depth": [None, 3, 5, 7],    # 单棵树最大深度（控制过拟合）
    "min_samples_split": [2, 5],     # 划分结点所需最小样本数
    "min_samples_leaf": [1, 2]       # 叶结点最少样本数
}

# 初始化网格搜索（5折交叉验证，评估指标为精度）
grid_search = GridSearchCV(
    estimator=RandomForestClassifier(random_state=42),
    param_grid=param_grid,
    cv=5,  # 5折交叉验证
    scoring="accuracy",  # 以精度为评估标准
    n_jobs=-1  # 利用所有CPU核心并行计算，加快调优速度
)

# 执行网格搜索（在训练集上找最优参数）
grid_search.fit(X_train, y_train)

# 输出最优参数与最优交叉验证精度
print("\n" + "="*50)
print("随机森林参数调优结果")
print("="*50)
print(f"最优参数组合：{grid_search.best_params_}")
print(f"最优交叉验证精度：{grid_search.best_score_:.2f}")

# 用最优参数模型在测试集上评估
best_rf = grid_search.best_estimator_  # 获取最优模型
y_test_best_pred = best_rf.predict(X_test)
best_test_acc = accuracy_score(y_test, y_test_best_pred)

print(f"\n最优模型测试集精度：{best_test_acc:.2f}")
print("最优模型测试集分类报告：")
print(classification_report(y_test, y_test_best_pred, target_names=["坏瓜", "好瓜"]))

6. 结果可视化（4 类核心图表）

通过可视化直观展示模型性能、特征重要性等关键信息，帮助理解随机森林的决策逻辑与效果：

# 设置中文字体（避免matplotlib中文乱码）
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建画布（2行2列，包含4个图表）
fig, axes = plt.subplots(2, 2, figsize=(15, 12))

# 1. 特征重要性可视化（柱状图）
feature_importance_sorted = feature_importance.sort_values(by="重要性")
axes[0, 0].barh(feature_importance_sorted["特征"], feature_importance_sorted["重要性"], color='#2E86AB')
axes[0, 0].set_xlabel("特征重要性")
axes[0, 0].set_title("随机森林特征重要性排序（好瓜分类）")
axes[0, 0].grid(axis='x', alpha=0.3)

# 2. 混淆矩阵可视化（热力图）
cm = confusion_matrix(y_test, y_test_best_pred)
sns.heatmap(
    cm, ax=axes[0, 1], annot=True, fmt='d', cmap='Blues',
    xticklabels=["坏瓜", "好瓜"], yticklabels=["坏瓜", "好瓜"]
)
axes[0, 1].set_xlabel("预测标签")
axes[0, 1].set_ylabel("真实标签")
axes[0, 1].set_title("最优模型混淆矩阵（测试集）")

# 3. 不同树数量（n_estimators）对精度的影响
n_estimators_list = [10, 20, 50, 100, 200, 300]
train_acc_list = []
test_acc_list = []

for n in n_estimators_list:
    temp_rf = RandomForestClassifier(n_estimators=n, random_state=42)
    temp_rf.fit(X_train, y_train)
    train_acc_list.append(accuracy_score(y_train, temp_rf.predict(X_train)))
    test_acc_list.append(accuracy_score(y_test, temp_rf.predict(X_test)))

axes[1, 0].plot(n_estimators_list, train_acc_list, marker='o', label="训练集精度", color='#A23B72')
axes[1, 0].plot(n_estimators_list, test_acc_list, marker='s', label="测试集精度", color='#F18F01')
axes[1, 0].set_xlabel("树的数量（n_estimators）")
axes[1, 0].set_ylabel("精度")
axes[1, 0].set_title("树的数量对随机森林精度的影响")
axes[1, 0].legend()
axes[1, 0].grid(alpha=0.3)

# 4. ROC曲线与AUC值（二分类任务核心评估图表）
y_test_proba = best_rf.predict_proba(X_test)[:, 1]  # 获取"好瓜"的预测概率
fpr, tpr, _ = roc_curve(y_test, y_test_proba)
roc_auc = auc(fpr, tpr)

axes[1, 1].plot(fpr, tpr, color='#C73E1D', lw=2, label=f'ROC曲线 (AUC={roc_auc:.2f})')
axes[1, 1].plot([0, 1], [0, 1], color='gray', lw=1, linestyle='--')  # 随机猜测线
axes[1, 1].set_xlabel("假正例率（FPR）")
axes[1, 1].set_ylabel("真正例率（TPR）")
axes[1, 1].set_title("最优模型ROC曲线与AUC值")
axes[1, 1].legend()
axes[1, 1].grid(alpha=0.3)

# 调整子图间距，保存图片（可直接插入CSDN推文）
plt.tight_layout()
plt.savefig("random_forest_melon_classification.png", dpi=300, bbox_inches='tight')
plt.show()

三、代码使用说明与入门建议

1. 数据集适配 ：若需替换为自己的数据集，只需修改 good_melon_data 字典中的特征与标签，确保文本特征保留 LabelEncoder 编码步骤，数值特征可直接使用。
2. 参数调优建议 ：
   • 入门阶段无需调优过多参数，重点关注 n_estimators（树的数量，通常 100~200 效果较好）和 max_depth（控制过拟合，建议 3~7）；
   • 若训练集精度远高于测试集（过拟合），可减小 max_depth 或增大 min_samples_split。
3. 结果解读重点 ：
   • 特征重要性图表可帮助筛选关键特征（如 "纹理" 对好瓜分类最重要，后续可优先保留）；
   • 混淆矩阵可直观看到模型误判情况（如 "把坏瓜误判为好瓜" 的数量）；
   • ROC 曲线与 AUC 值：AUC 越接近 1，模型区分 "好瓜" 与 "坏瓜" 的能力越强。