运动学模型推导 + 离散化 + 工程化版本（适用于前方单舵轮 AGV / 自动驾驶 / MPC）

模型推导：

前言

[一、自行车模型结构（Bicycle Model）](#一、自行车模型结构（Bicycle Model）)

[二、速度分解 ------ 最关键的一步](#二、速度分解 —— 最关键的一步)

[三、无侧滑约束（No-Slip Constraint）](#三、无侧滑约束（No-Slip Constraint）)

[四、角速度推导（Yaw Rate）](#四、角速度推导（Yaw Rate）)

五、世界坐标系下速度

[六、最终连续时间模型（Continuous Model）](#六、最终连续时间模型（Continuous Model）)

[七、扩展输入：用加速度 & 转角速度作为控制量（工程常用）](#七、扩展输入：用加速度 & 转角速度作为控制量（工程常用）)

1）转角速度解释：

[2）为什么控制输入不是 δ 而是 δ˙](#2）为什么控制输入不是 δ 而是 δ˙)

[3）更工程的解释：转角速度 = 转向电机的目标速度](#3）更工程的解释：转角速度 = 转向电机的目标速度)

[八、离散化（用于 MPC / 仿真 / 代码实现）](#八、离散化（用于 MPC / 仿真 / 代码实现）)

[九、小角度线性化（用于 LQR、线性 MPC）](#九、小角度线性化（用于 LQR、线性 MPC）)

十、完整可复用模型总结（最终工程版）

1）连续时间模型（工程常用）：

[2）离散时间模型（MPC 直接可用）：](#2）离散时间模型（MPC 直接可用）：)

[3）小角度线性化（用于 LQR）](#3）小角度线性化（用于 LQR）)

[十一、适用范围](#十一、适用范围)

1）使用本模型的情况

2）不适使用的情况

模型推导

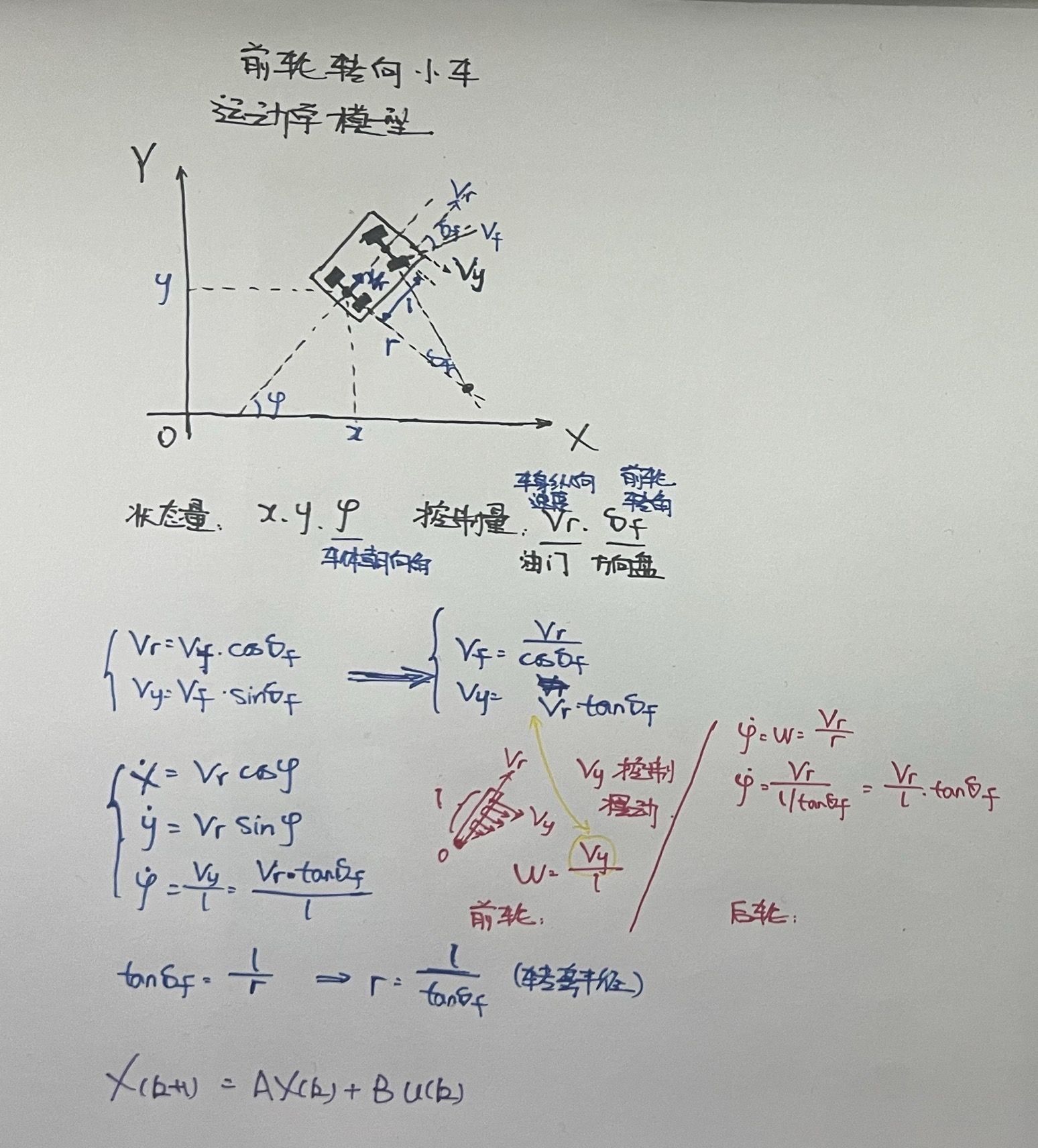
在之前的章节里，我已经把 MPC 的核心数学结构推到了一遍：
离散模型 → 预测矩阵 X=Fxk+GU → 构造代价函数 → 变成一个标准二次规划（QP）问题

以及对约束的设定和QP求解器的运用进行的详细的讲解

具体文章见下：

MPC模型预测控制原理全解析：从状态预测、矩阵推导到QP求解与滚动优化（含完整手推过程）-CSDN博客https://blog.csdn.net/m0_58954356/article/details/154781300?spm=1001.2014.3001.5501 MPC 里的约束与 QP 求解器实战------从原理、例子到 C++ 落地-CSDN博客https://blog.csdn.net/m0_58954356/article/details/154830088?spm=1001.2014.3001.5501 MPC模型预测控制：从基本概念到数学推导（基于 DR_CAN 课堂笔记整理）-CSDN博客https://blog.csdn.net/m0_58954356/article/details/154800788?spm=1001.2014.3001.5501

前言

运动学模型（Kinematic Bicycle Model）是自动驾驶中最常用的底层模型之一，它是如下算法的基础：

MPC（Model Predictive Control）
LQR 路径跟踪
Stanley / Pure Pursuit
Frenet 轨迹规划
Kalman Filter / 状态估计
AGV 前方单舵轮控制

然而，大多数资料只给出三行公式：

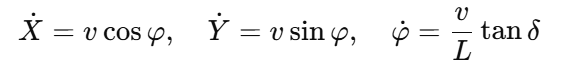
却没有讲清楚它们的来源、意义、适用范围以及工程化写法。

本文将一次讲透：

从几何 → 速度分解 → 无侧滑约束 → 世界系转换 → 离散化 → 工程实现 → AGV 单舵轮版本。

让你彻底搞懂运动学模型。

一、自行车模型结构（Bicycle Model）

将四轮车等效为：

后轴一个点
前轴一个点
轴距固定为 LLL
前轮可转向（角度 δf\delta_fδf）
后轮不可转向

车辆状态：

输入量（控制量）：

vr：车辆（后轮/车体）纵向速度
δf：前轮转角

二、速度分解 ------ 最关键的一步

前轮打了角后，前轮速度方向不再与车体一致。

前轮速度 vfv_fvf 在车体坐标系分解：

从第一行：

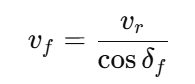
代入第二行：

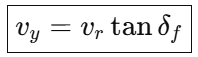
打方向盘后，车辆产生的**"侧向速度分量"，也是车辆开始转弯的根本原因**。

三、无侧滑约束（No-Slip Constraint）

轮胎允许沿自身方向滚动，但不允许横向滑动。

因此车辆绕某个瞬时圆心 ICR 运动。

几何关系：

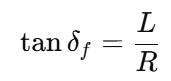
得转弯半径：

四、角速度推导（Yaw Rate）

后轮速度：vr

绕圆心半径：R

所以角速度为：

代入上一步：

这是现代控制器（MPC/LQR）最常见的 yaw rate 模型。

五、世界坐标系下速度

车体速度 vr 方向与世界系的夹角为 φ ，所以：

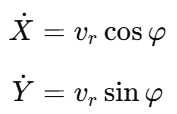
六、最终连续时间模型（Continuous Model）

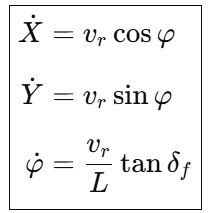
这是运动学自行车模型的标准形式。

七、扩展输入：用加速度 & 转角速度作为控制量（工程常用）

实际车辆 ECU 不能直接控制：

速度 vr（而是加速度 a）
转角 δf（而是转角速度 δ˙）

因此加入动力学状态：

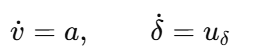
扩展状态：

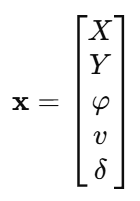
扩展模型：

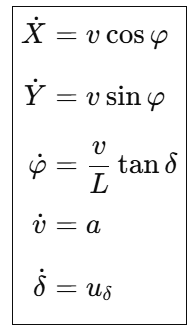
这是自动驾驶 MPC 最常用的 非线性运动学模型。

1）转角速度解释：

转角速度 不是车的角速度（车身转弯的 Yaw rate）

而是：

方向盘打角的变化速度
也就是前轮转角 δ 时间导数

简单说：

δ：前轮当前打了多少角
δ˙：前轮"转向动作"变化的速度

就像...

人转方向盘时 → δ 在变化
你转得快一点 → δ˙ 大
你转得慢一点 → δ˙ 小

单位通常是：

rad/s（自动驾驶控制使用）
deg/s（汽车标定使用）

2）为什么控制输入不是 δ 而是 δ˙

因为真实车辆有转向执行器，包含：

电机
减速机
力反馈
机械限位
最大加速度/角速度

这些执行器不能让你"瞬间跳到某个转角"。

比如：

你不可能一下把方向盘从 0° 打到 30°，总要一个过程！

这个过程由转角速度 δ˙ 决定。

所以真实 ECU 接受的是：

控制量	含义
a	油门/刹车产生的加速度
δ˙	转向执行器的角速度指令

而不是：

不直接控制
v（车辆速度）
δ（方向盘角度）

这些都是最终结果。

3）更工程的解释：转角速度 = 转向电机的目标速度

在 AGV / 无人叉车 / 汽车中，转角是通过"转向电机"驱动的。

电机控制里常见的闭环结构：

bash 复制代码

目标转角 δ_target  
→ 误差 = δ_target - δ_measured  
→ PID 控制  
→ 得到需要的 转角速度 δ˙  
→ 由伺服驱动器控制执行器

所以控制器给 ECU 的信号一般是：方向盘转速（电机角速度）

而不是：让方向盘瞬间转到 15°

因为那样不符合执行器的物理机制。

八、离散化（用于 MPC / 仿真 / 代码实现）

最常用离散化：Euler 前向差分

采样周期 T

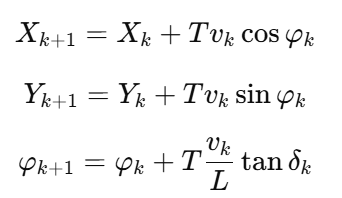
如果带动态输入：

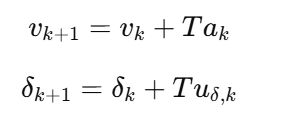
离散后的完整形式：

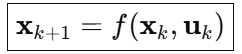
这是 MPC 一定要用的版本。

九、小角度线性化（用于 LQR、线性 MPC）

对于低速 & 小转角：

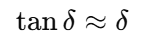
线性化得到：

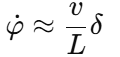
线性模型可写成：

运动学模型推导 + 离散化 + 工程化版本（适用于前方单舵轮 AGV / 自动驾驶 / MPC）

模型推导

前言

一、自行车模型结构（Bicycle Model）

二、速度分解 ------ 最关键的一步

三、无侧滑约束（No-Slip Constraint）

四、角速度推导（Yaw Rate）

五、世界坐标系下速度

六、最终连续时间模型（Continuous Model）

七、扩展输入：用加速度 & 转角速度作为控制量（工程常用）

1）转角速度解释：

2）为什么控制输入不是 δ 而是 δ˙

3）更工程的解释：转角速度 = 转向电机的目标速度

八、离散化（用于 MPC / 仿真 / 代码实现）

九、小角度线性化（用于 LQR、线性 MPC）

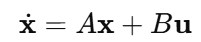
十、完整可复用模型总结

1）连续时间模型（工程常用）：

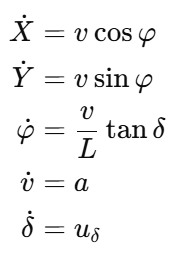
2）离散时间模型（MPC 直接可用）：

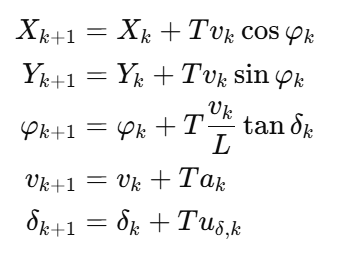
3）小角度线性化（用于 LQR）

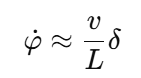
十一、 适用范围

1）使用本模型的情况

2）不适使用的情况

十一、适用范围