01BFS学习笔记 - 技术栈

基本思路

使用deque，保证更优路径先被处理 ，只记录最优信息 ，所以一旦 dist 更新就不再更新，不需要额外松弛。
- 如果当前边权为 0，则将目标节点加入队首；
- 如果当前边权为 1，则将目标节点加入队尾。
注意当图的边权都是0/1的时候才能用

板子题

P4554

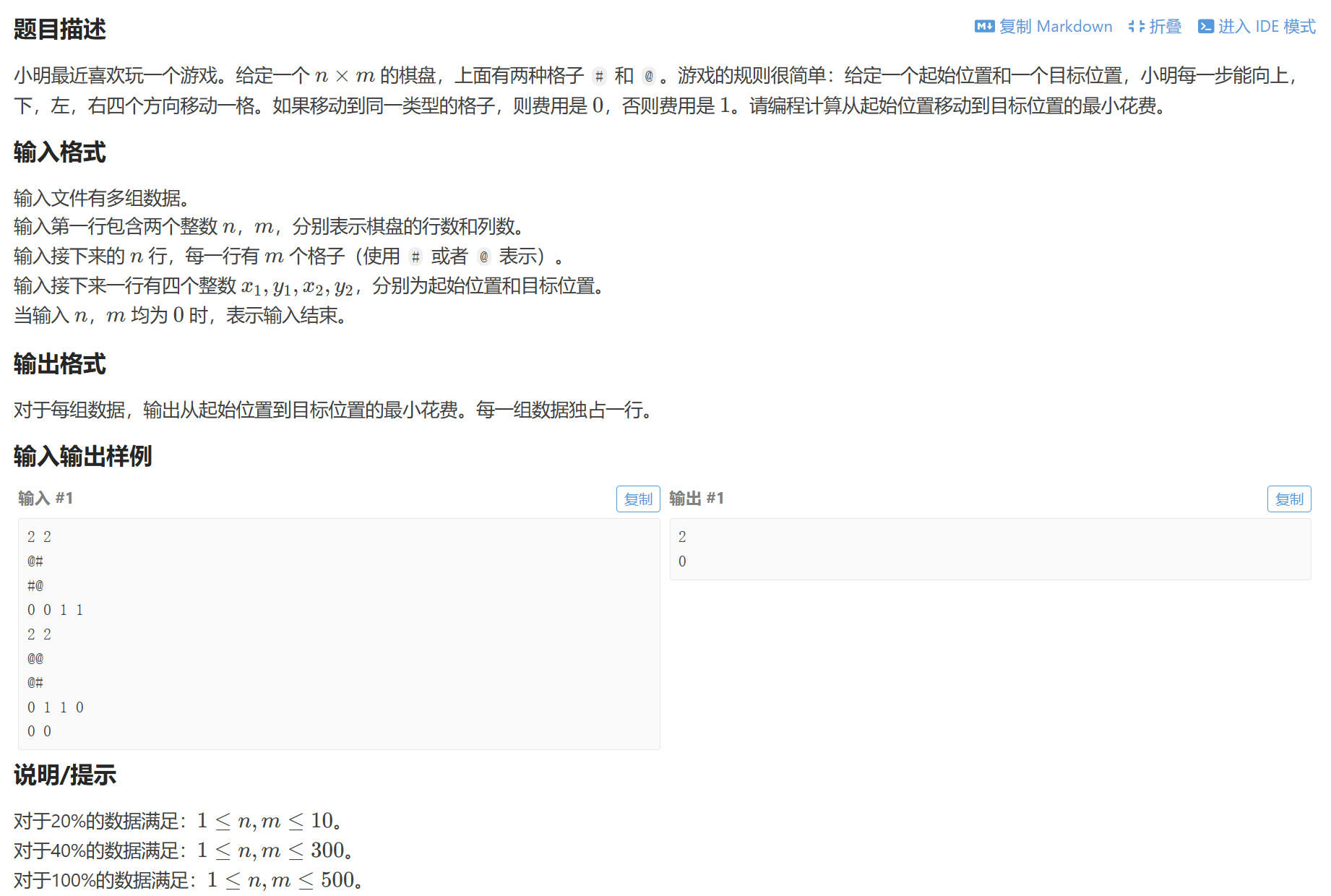
cpp 复制代码

const int N=500,inf=1e18,mod=998244353;
string a[N];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int dis[N][N];
void solve()
{
    int n,m;
    while(cin>>n>>m&&n&&m){
        forr(i,0,n-1){
            cin>>a[i];
        }
        forr(i,0,n-1)forr(j,0,m-1)dis[i][j]=inf;//要记录路径最小值 先初始化为最大值
        int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;
        deque<pii>q;
        //原点入队
        q.push_back({x1,y1});dis[x1][y1]=0;
        
        int ans=1e18;
        while(q.size()){
            auto [x,y]=q.front();
            q.pop_front();
            char c=a[x][y];
            
            forr(i,0,3){//遍历下一步
                int nx=x+dx[i],ny=y+dy[i],ndis;//ndis记录走到(nx,ny)的代价，确定是最优才会放入dis数组和deque
                //判断边界
                if(nx>n-1||ny>m-1||nx<0||ny<0)continue;
                //计算代价
                if(c==a[nx][ny])ndis=dis[x][y];
                else ndis=dis[x][y]+1;
                //如果到了目的地 更新答案
                if(nx==x2&&ny==y2)ans=min(ndis,ans);
                //确认最优
                if(ndis<dis[nx][ny]){
                    dis[nx][ny]=ndis;
                    if(c==a[nx][ny])q.push_front({nx,ny});//本次不用消耗代价 贪心地认为是更优的 放到队首
                    else q.push_back({nx,ny});//本次消耗代价的放在队尾
                }
            }
        }
        cout<<ans<<endl;
    }
}

P1948 二分+01BFS

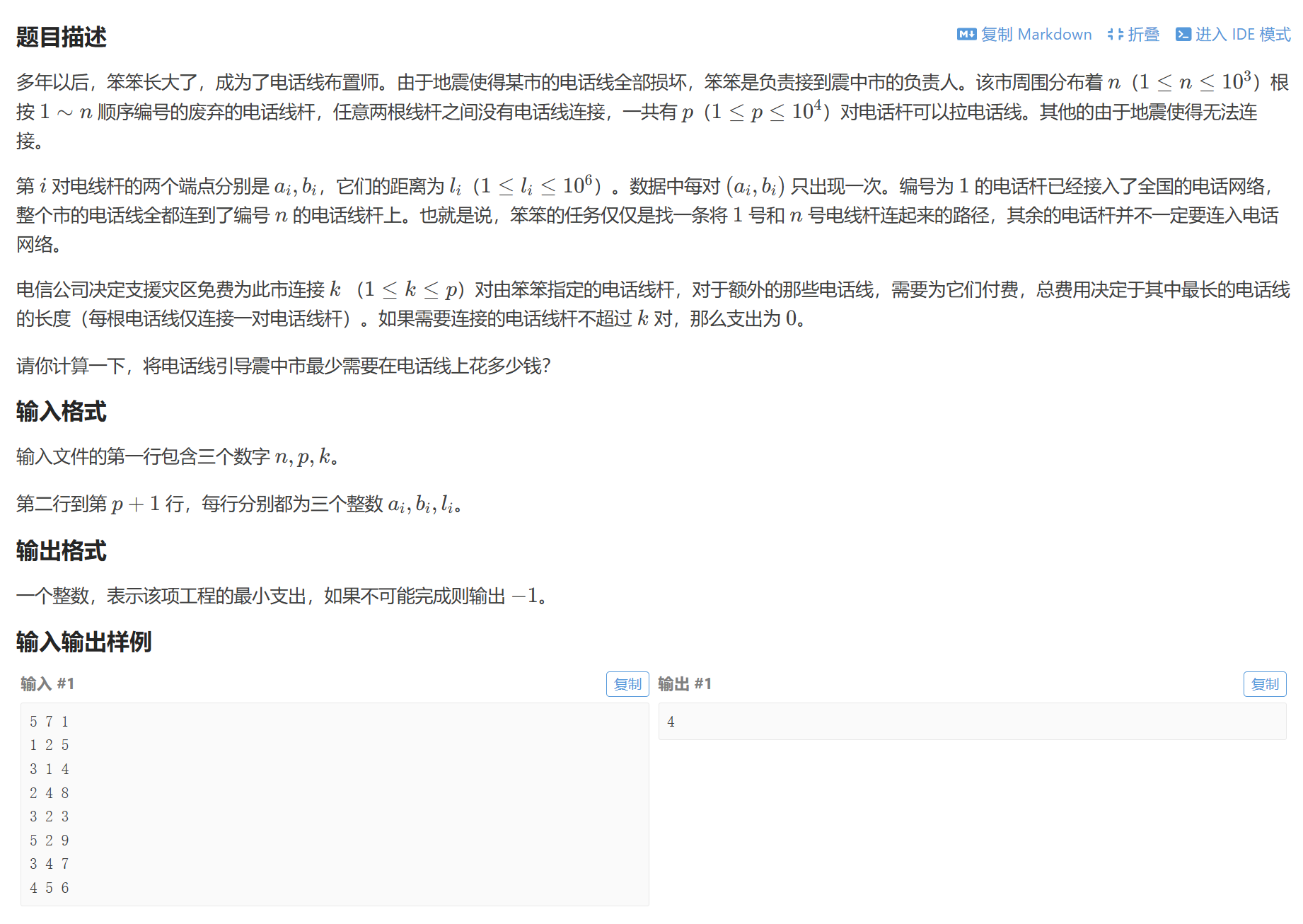
cpp 复制代码

const int N=1e3+10,M=6e3+10,mod=998244353,inf=1e18;
//"最少"成本 免费k个就选最长的k个 
//总费用决定于其中最长的电话线的长度 二分需要花钱的最大值
vector<pii>g[N];
int n,p,k;
int dis[N];
bool check(int x){
    // forr(i,1,n)forr(j,1,n)dis[i][j]=inf;
    forr(i,1,n)dis[i]=inf;
    deque<int>q;
    q.push_back(1);dis[1]=0;
    while(q.size()){
        int now=q.front();q.pop_front();
        for(auto [nxt,len]:g[now]){
            int nd;
            if(len<=x)nd=dis[now];
            else nd=dis[now]+1;

            if(nd<dis[nxt]){
                dis[nxt]=nd;
                if(len>x)q.push_back(nxt);
                else q.push_front(nxt);
            }
        }
    }
    return dis[n]<=k;
}
void solve(){
    cin>>n>>p>>k;
    forr(i,1,p){
        int a,b,l;cin>>a>>b>>l;
        g[a].push_back({b,l});
        g[b].push_back({a,l});
    }
    int l=0,r=1e7;//二分最长的付费长度
    int ans=-1;
    while(l<r){
        int mid=(l+r)>>1;
        if(check(mid))r=mid,ans=mid;
        else l=mid+1;
    }
    cout<<ans<<endl;
}