目录
一:单词搜索
1.1题目

题目链接:https://leetcode.cn/problems/word-search/
1.2算法原理
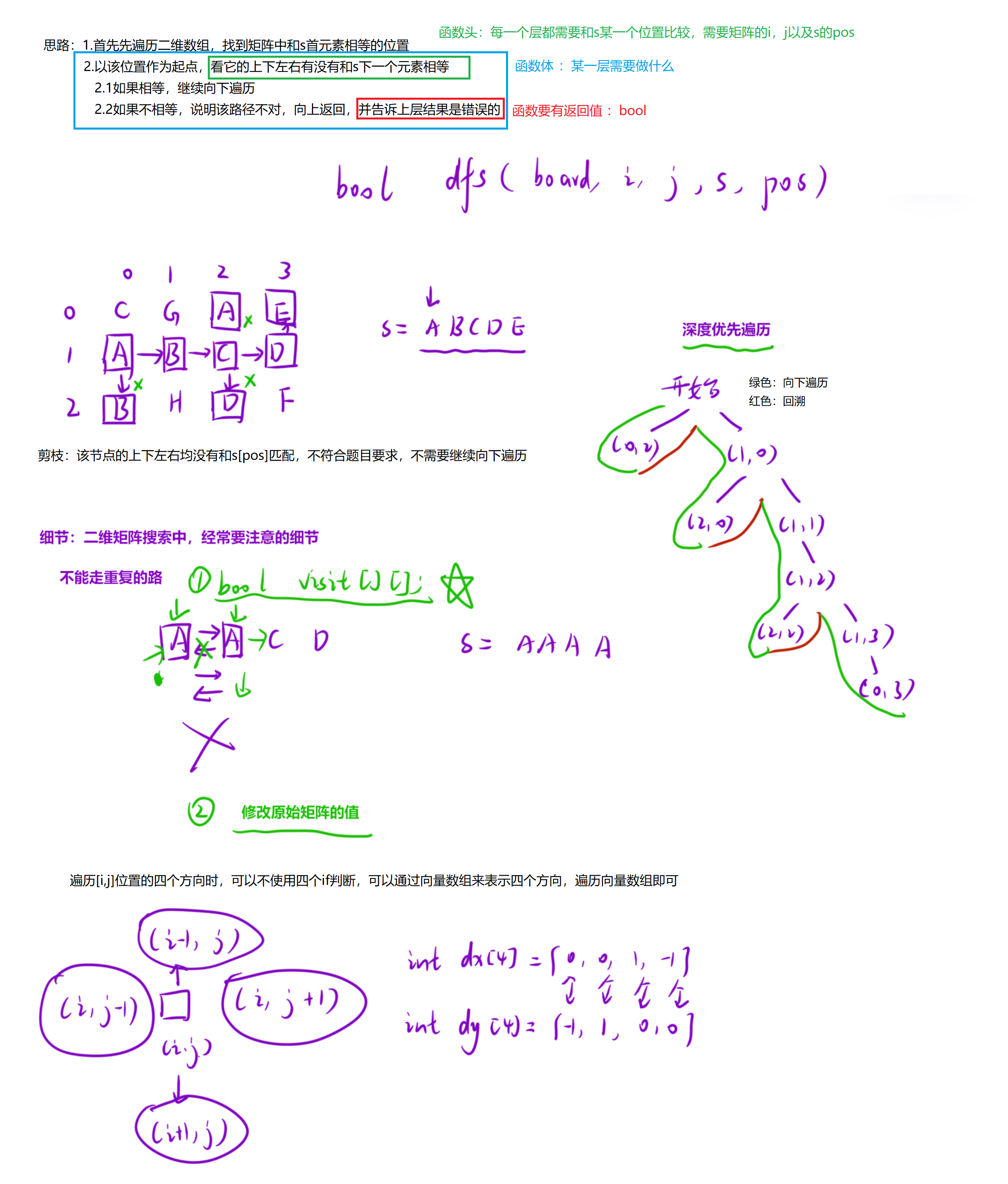
1.3代码
cpp
class Solution {
public:
bool vis[7][7];//查看该位置是否已经走过
int m = 0 ,n = 0;
string word;
bool exist(vector<vector<char>>& board, string _word)
{
m = board.size();
n = board[0].size();
word = _word;
//确定矩阵中的第一个位置
for(int i = 0; i < m; i++)
for(int j = 0; j <n; j++)
{
if(board[i][j] == word[0])
{
vis[i][j] = true;
if(dfs(board,i,j,1)) return true;
vis[i][j] = false;
}
}
return false;
}
int dx[4] = {0,0 ,-1,1};
int dy[4] = {-1,1,0,0};
bool dfs(vector<vector<char>>& board,int i,int j, int pos)
{
if(pos == word.size()) return true;
//使用向量组标记方位
for(int k = 0; k < 4;k++)
{
int x = i+dx[k],y = j+dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && board[x][y] == word[pos])
{
vis[x][y] = true;
if(dfs(board,x,y,pos+1)) return true;
vis[x][y] = false;
}
}
return false;
}
};二:黄金矿工
2.1题目

题目链接:https://leetcode.cn/problems/path-with-maximum-gold/
2.2算法原理
本题的算法原理的思路和代码的逻辑和上一题的单词搜索是一致的

2.3代码
cpp
class Solution {
public:
bool vis[16][16];
int sum = 0,ret = 0;
int m = 0, n = 0;
int getMaximumGold(vector<vector<int>>& grid)
{
m = grid.size();
n = grid[0].size();
for(int i = 0; i < m; i++)
for(int j = 0; j < n;j++)
{
if(grid[i][j] != 0)
{
vis[i][j] = true;
sum += grid[i][j];
dfs(grid,i,j);
vis[i][j] = false;
sum -= grid[i][j];
}
}
return ret;
}
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
void dfs(vector<vector<int>>& grid,int i, int j)
{
for(int k = 0; k < 4;k++)
{
int x = i + dx[k],y = j+dy[k];
if(x >= 0&& x <m &&y >= 0 && y < n && !vis[x][y]&& grid[x][y] != 0)
{
sum += grid[x][y];
vis[x][y] = true;
dfs(grid,x,y);
sum -= grid[x][y];
vis[x][y] = false;
}
}
ret = max(ret,sum);
}
};三:不同路径III
3.1题目

题目链接:https://leetcode.cn/problems/unique-paths-iii/description/
3.2算法原理
算法原理和前面两个题都是相似的
1.首先遍历数组,找到起点
2.然后从起点出发,上下左右四个方向找空方格,直到找到终点数字2
细节:1.题目要求每一个空方格都要走一遍,所以刚开始可以先遍历一遍查看空方格总量,然后深度遍历的时候,step++,直到step和之前统计的数量相等为止
2.不能走重复的空格子,使用bool数组标记已经走过的位置
3.四个方向使用向量数组
4.递归出口:step == 空方格+起点终点 并且位于数字2的方格
5.剪枝:方格为-1时剪枝
3.3代码
cpp
class Solution {
public:
int m = 0, n = 0;
bool vis[21][21];
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
int ret = 0, step = 1,cont = 0;
int uniquePathsIII(vector<vector<int>>& grid)
{
m = grid.size();
n = grid[0].size();
int bx = 0, by =0;
for(int i = 0; i < m;i++)
for(int j = 0; j <n; j++)
{
//统计路径长度
if(grid[i][j] == 0)
{
cont++;
}
else if(grid[i][j] == 1)
{
bx = i;
by = j;
}
}
cont += 2;//加上路径的起点和终点
vis[bx][by] = true;
dfs(grid,bx,by);
return ret;
}
void dfs(vector<vector<int>>& grid,int i, int j)
{
if(grid[i][j] == 2)
{
if(cont == step) ret++;
return;
}
for(int k = 0; k < 4;k++)
{
int x = i +dx[k],y = j + dy[k];
if(x >= 0 && x < m&& y>=0 && y < n &&!vis[x][y] && grid[x][y] != -1)
{
vis[x][y] = true;
step++;
dfs(grid,x,y);
step--;
vis[x][y] = false;
}
}
}
};