全排列
时间限制:1000ms 内存限制:128MB 栈限制:128MB
题目描述
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。 我们假设对于小写字母有'a' <'b' < ... <'y'<'z',而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入格式
只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在1到6之间。
输出格式
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。
字母序如下定义:
已知 S = s 1 s 2 . . . s k S=s_{1}s_{2}...s_{k} S=s1s2...sk
则S<T等价于,存在p(1<=p<=k),使得s1=t1,s2=t2,...,sp−1=tp−1,sp<tp成立。
样例
样例 1 输入:
abc
样例 1 输出:
abc
acb
bac
bca
cab
cba
样例解析
(空)
数据规模
(空)
问题分析
全排列的意思:
abc是一个长度为3的字符串
把abc拆成a,b,c
能有多少种排列组合
全部输出
如abc有6种组合,则输出
abc
acb
bac
bca
cab
cba
目标是输出当前字符串的所有排列组合,不用输出个数
思路 肯定没人看
这道题我用的深搜 我在想能不能打表
当然不能打表 能累死人
他的组合有很多种,还有不同的字母的排列组合,这样会死
所以用深搜
先以例子abc来看
接下来是第一位选择a的图片
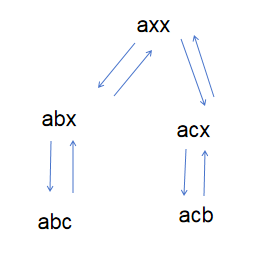
第一位选择了a
第二位又选择了b
第三位选择了c
组成abc
发现没有任何组合,回溯到有另外组合的选择时候
第一位选择了a
第二位选择了c
第三位选择了b
组成acb
发现没有任何组合,回溯到有另外组合的选择时候
以上为第一位选择a的情况
以此类推,我们可以这样:
第一位选择了b
第二位选择了a
第三位选择了c
组成bac
发现没有任何组合,回溯到有另外组合的选择时候
第一位选择了b
第二位选择了c
第三位选择了a
组成bca
发现没有任何组合,回溯到有另外组合的选择时候
第一位选择了c
第二位选择了a
第三位选择了b
组成cab
发现没有任何组合,回溯到有另外组合的选择时候
第一位选择了c
第二位选择了b
第三位选择了a
组成cba
发现没有任何组合,回溯到有另外组合的选择时候
没有其他选择,跳出
这就是深搜
本质就是不断地寻找,走不通了就回溯,直到回溯到有另外选择的时候
cpp
void dfs(int u){//u代表第u个格子
if(u==n+1){//出口,当遍历到了n+1就无法继续遍历
for(int i=1;i<=n;i++){
printf("%c",s[path[i]-1]);//输出得出的结果
}
puts("");
return ;//跳出去
}
for(int i=1;i<=n;i++){
if(st[i]==false){//没用过
st[i]=true;//用过了
path[u]=i;//试了当前可以的数
dfs(u+1);//递归一遍,继续搜索一遍
st[i]=false;//回溯,否则就不能再的到其他的结果
}
}
}以上便是核心代码(具体看注释)
代码
cpp
//在想
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
int path[10001];
bool st[10010];//true代表用过
void dfs(int u){//u代表第u个格子
if(u==n+1){//出口,当遍历到了n+1就无法继续遍历
for(int i=1;i<=n;i++){
printf("%c",s[path[i]-1]);//输出得出的结果
}
puts("");
return ;//跳出去
}
for(int i=1;i<=n;i++){
if(st[i]==false){//没用过
st[i]=true;//用过了
path[u]=i;//试了当前可以的数
dfs(u+1);//递归一遍,继续搜索一遍
st[i]=false;//回溯,否则就不能再的到其他的结果
}
}
}
int main(){
cin>>s;
n=s.size();
dfs(1);
return 0;
}完结撒花!