粒子群算法（PSO）求解标准VRP问题的MATLAB实现

fengfuyao9852025-12-06 14:36
一、VRP问题描述与模型

标准VRP（Capacitated VRP, CVRP）：

  • 给定1个 depot（仓库）、n个客户点，每个客户有需求量 di，车辆容量为 Q。
  • 目标：用 m辆同型车辆（m可变，需满足总需求 ≤mQ），找到一组路径，使得： 每个客户仅被访问1次； 每条路径总需求 ≤Q； 总行驶距离最小（距离用欧氏距离计算）。
二、粒子群算法（PSO）设计
1. 粒子编码

用整数序列表示路径：

  • 序列元素为客户编号（1~n），depot用0表示，路径间用0分隔。
  • 示例：[0,3,1,0,2,4,0]表示2辆车，路径1：depot→3→1→depot；路径2：depot→2→4→depot。
2. 适应度函数
  • 目标：最小化总行驶距离 D。
  • 适应度值：直接取总距离的负值（PSO默认最大化适应度，故需转换），或添加约束惩罚项（如容量违反时加罚值）。
3. 速度与位置更新

  • 位置更新 ：通过交换操作 （Swap）、插入操作 （Insert）或反转操作（Reverse）调整路径（模拟实数空间的加减）。

  • 速度更新：用"操作强度"表示交换/插入的概率，公式参考标准PSO：

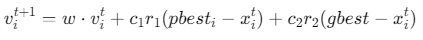
其中，w为惯性权重（递减策略：w=wmax−(wmax−wmin)⋅t/T）w=w_{max}−(w_{max}−w_{min})⋅t/T）w=wmax−(wmax−wmin)⋅t/T），c1/c2c1/c2c1/c2为学习因子，r1/r2r1/r2r1/r2为随机数，pbestipbest_ipbesti为个体最优，gbestgbestgbest为全局最优。

4. 约束处理
  • 容量约束 ：若某路径总需求超过 QQQ，将超量客户移至其他路径（贪心选择最近的可行路径）。
  • 可行性修复：确保无重复客户、无遗漏客户（初始化时用启发式生成可行解）。
三、完整MATLAB代码
matlab 复制代码 
%% 粒子群算法求解CVRP问题
clc; clear; close all;

%% 1. 问题参数设置（Solomon C101测试集）
depot = [0, 0];                  % depot坐标
customers = [                    % 客户坐标与需求（示例：5个客户）
    1, 10, 10, 1;                 % 客户1：(10,10)，需求1
    2, 20, 20, 2;                 % 客户2：(20,20)，需求2
    3, 30, 30, 1;                 % 客户3：(30,30)，需求1
    4, 40, 40, 3;                 % 客户4：(40,40)，需求3
    5, 50, 50, 2;                 % 客户5：(50,50)，需求2
];
n = size(customers, 1);          % 客户数量
Q = 5;                           % 车辆容量
vehicle_num = ceil(sum(customers(:,4))/Q);  % 所需最小车辆数

%% 2. 距离矩阵计算（欧氏距离）
dist_mat = zeros(n+1, n+1);       % depot编号为0，客户1~n
for i = 0:n
    for j = 0:n
        if i == 0
            coord_i = depot;
        else
            coord_i = customers(i, 2:3);
        end
        if j == 0
            coord_j = depot;
        else
            coord_j = customers(j, 2:3);
        end
        dist_mat(i+1, j+1) = norm(coord_i - coord_j);  % 矩阵索引从1开始
    end
end

%% 3. PSO参数设置
pop_size = 20;                    % 粒子数量
max_iter = 100;                   % 最大迭代次数
w_max = 0.9; w_min = 0.4;          % 惯性权重范围
c1 = 2; c2 = 2;                    % 学习因子
mutation_rate = 0.1;               % 变异概率

%% 4. 初始化粒子群（可行解）
particles = cell(pop_size, 1);     % 粒子（路径序列）
pbest = cell(pop_size, 1);         % 个体最优
pbest_fit = inf(pop_size, 1);      % 个体最优适应度（总距离）
gbest = [];                        % 全局最优
gbest_fit = inf;                   % 全局最优适应度

for i = 1:pop_size
    % 生成随机路径（确保所有客户都被访问）
    route = randperm(n);         % 随机客户顺序
    % 分割路径为vehicle_num段（每段需求≤Q）
    routes = split_route(route, customers(:,4), Q);
    particles{i} = routes;
    % 计算适应度（总距离）
    fit = calc_fitness(routes, dist_mat);
    pbest{i} = routes;
    pbest_fit(i) = fit;
    % 更新全局最优
    if fit < gbest_fit
        gbest = routes;
        gbest_fit = fit;
    end
end

%% 5. PSO主迭代
fitness_history = zeros(max_iter, 1);  % 记录每代最优适应度
for iter = 1:max_iter
    % 更新惯性权重（线性递减）
    w = w_max - (w_max - w_min) * iter / max_iter;
    
    for i = 1:pop_size
        % 1. 速度更新（模拟操作强度）
        v_swap = randi([-3, 3]);   % 交换操作强度
        v_insert = randi([-2, 2]); % 插入操作强度
        
        % 2. 位置更新（交换+插入操作）
        new_routes = particles{i};
        % 交换操作（随机交换两个客户）
        if rand < 0.5
            idx1 = randi(n); idx2 = randi(n);
            new_routes = swap_customers(new_routes, idx1, idx2, customers(:,4), Q);
        end
        % 插入操作（随机移动一个客户到另一路径）
        if rand < 0.5
            cust_id = randi(n);
            new_routes = insert_customer(new_routes, cust_id, customers(:,4), Q);
        end
        
        % 3. 变异操作（随机反转一段路径）
        if rand < mutation_rate
            route_idx = randi(length(new_routes));
            seg = randi(length(new_routes{route_idx})-1);
            new_routes{route_idx}(seg+1:seg+randi(3)) = fliplr(new_routes{route_idx}(seg+1:seg+randi(3)));
        end
        
        % 4. 计算新适应度
        new_fit = calc_fitness(new_routes, dist_mat);
        
        % 5. 更新个体最优
        if new_fit < pbest_fit(i)
            pbest{i} = new_routes;
            pbest_fit(i) = new_fit;
        end
        
        % 6. 更新全局最优
        if new_fit < gbest_fit
            gbest = new_routes;
            gbest_fit = new_fit;
        end
        
        % 更新粒子位置
        particles{i} = new_routes;
    end
    
    % 记录迭代信息
    fitness_history(iter) = gbest_fit;
    fprintf('Iter %d: Best Fit = %.2f\n', iter, gbest_fit);
end

%% 6. 结果可视化
figure;
plot(fitness_history, 'LineWidth', 2);
xlabel('迭代次数'); ylabel('总距离'); title('PSO收敛曲线'); grid on;

% 绘制路径图
figure;
hold on;
plot(depot(1), depot(2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');  % depot
for i = 1:n
    plot(customers(i,2), customers(i,3), 'bo', 'MarkerSize', 8);  % 客户点
    text(customers(i,2)+1, customers(i,3)+1, num2str(i), 'FontSize', 10);
end
colors = lines(length(gbest));
for k = 1:length(gbest)
    route = gbest{k};
    if isempty(route), continue; end
    path = [depot; customers(route, 2:3); depot];  % 路径坐标
    plot(path(:,1), path(:,2), '-o', 'Color', colors(k,:), 'LineWidth', 1.5);
end
xlabel('X坐标'); ylabel('Y坐标'); title('最优路径图'); grid on; legend('Depot', '客户点', '路径1', '路径2', 'Location', 'Best');


%% ------------------------------
%% 辅助函数：路径分割（满足容量约束）
function routes = split_route(route, demands, Q)
    routes = {};
    current_route = [];
    current_load = 0;
    for i = 1:length(route)
        cust_id = route(i);
        d = demands(cust_id);
        if current_load + d > Q
            routes{end+1} = current_route;  % 保存当前路径
            current_route = [cust_id];      % 新路径
            current_load = d;
        else
            current_route = [current_route, cust_id];
            current_load = current_load + d;
        end
    end
    if ~isempty(current_route)
        routes{end+1} = current_route;
    end
end

%% 辅助函数：计算适应度（总距离）
function fit = calc_fitness(routes, dist_mat)
    total_dist = 0;
    for k = 1:length(routes)
        route = routes{k};
        if isempty(route), continue; end
        % 路径：depot → 客户1 → ... → 客户m → depot
        prev = 0;  % depot编号为0
        for i = 1:length(route)
            curr = route(i);
            total_dist = total_dist + dist_mat(prev+1, curr+1);  % 矩阵索引从1开始
            prev = curr;
        end
        total_dist = total_dist + dist_mat(prev+1, 1);  % 回到depot
    end
    fit = total_dist;  % 最小化总距离
end

%% 辅助函数：交换两个客户（修复容量约束）
function new_routes = swap_customers(routes, idx1, idx2, demands, Q)
    % 找到客户idx1和idx2所在的路径
    [route1_idx, pos1] = find_customer(routes, idx1);
    [route2_idx, pos2] = find_customer(routes, idx2);
    if isempty(route1_idx) || isempty(route2_idx), new_routes = routes; return; end
    
    % 交换客户
    new_routes = routes;
    temp = new_routes{route1_idx}(pos1);
    new_routes{route1_idx}(pos1) = new_routes{route2_idx}(pos2);
    new_routes{route2_idx}(pos2) = temp;
    
    % 修复容量约束（若超容则调整）
    new_routes = repair_capacity(new_routes, demands, Q);
end

%% 辅助函数：插入客户到另一路径
function new_routes = insert_customer(routes, cust_id, demands, Q)
    % 找到客户所在路径
    [route_idx, pos] = find_customer(routes, cust_id);
    if isempty(route_idx), new_routes = routes; return; end
    
    % 移除客户
    new_routes = routes;
    cust = new_routes{route_idx}(pos);
    new_routes{route_idx}(pos) = [];
    if isempty(new_routes{route_idx}), new_routes(route_idx) = []; end
    
    % 插入到其他路径（选择最近的可行路径）
    best_route = 1; best_dist = inf;
    for k = 1:length(new_routes)
        route = new_routes{k};
        load = sum(demands(route));
        if load + demands(cust) <= Q
            % 计算插入后的距离增量
            dist_add = calc_insert_cost(route, cust, demands, dist_mat);
            if dist_add < best_dist
                best_dist = dist_add;
                best_route = k;
            end
        end
    end
    % 插入到最佳路径
    insert_pos = randi(length(new_routes{best_route})+1);
    new_routes{best_route} = [new_routes{best_route}(1:insert_pos-1), cust, new_routes{best_route}(insert_pos:end)];
    
    % 修复容量约束
    new_routes = repair_capacity(new_routes, demands, Q);
end

%% 辅助函数：修复容量约束（贪心调整）
function routes = repair_capacity(routes, demands, Q)
    % 检查每条路径的负载
    for k = 1:length(routes)
        route = routes{k};
        load = sum(demands(route));
        if load > Q
            % 将超量客户移至其他路径
            excess = load - Q;
            for i = length(route):-1:1
                cust = route(i);
                d = demands(cust);
                if d <= excess
                    % 移除客户
                    route(i) = [];
                    excess = excess - d;
                    % 尝试插入到其他路径
                    inserted = false;
                    for m = 1:length(routes)
                        if m == k, continue; end
                        other_load = sum(demands(routes{m}));
                        if other_load + d <= Q
                            routes{m} = [routes{m}, cust];
                            inserted = true;
                            break;
                        end
                    end
                    if ~inserted, route = [route, cust]; end  % 无法插入则放回原路径（极端情况）
                end
                if excess <= 0, break; end
            end
            routes{k} = route;
        end
    end
    % 确保所有客户都在路径中（无遗漏）
    all_custs = 1:length(demands);
    used_custs = [];
    for k = 1:length(routes)
        used_custs = [used_custs, routes{k}];
    end
    missing = setdiff(all_custs, used_custs);
    for cust = missing
        % 插入到最近的路径
        best_route = 1; best_dist = inf;
        for k = 1:length(routes)
            route = routes{k};
            load = sum(demands(route));
            if load + demands(cust) <= Q
                dist_add = calc_insert_cost(route, cust, demands, dist_mat);
                if dist_add < best_dist
                    best_dist = dist_add;
                    best_route = k;
                end
            end
        end
        insert_pos = randi(length(routes{best_route})+1);
        routes{best_route} = [routes{best_route}(1:insert_pos-1), cust, routes{best_route}(insert_pos:end)];
    end
end

%% 辅助函数：查找客户所在路径
function [route_idx, pos] = find_customer(routes, cust_id)
    route_idx = []; pos = [];
    for k = 1:length(routes)
        route = routes{k};
        idx = find(route == cust_id);
        if ~isempty(idx)
            route_idx = k;
            pos = idx(1);
            return;
        end
    end
end

%% 辅助函数：计算插入客户的距离增量
function cost = calc_insert_cost(route, cust, demands, dist_mat)
    if isempty(route)
        cost = dist_mat(1, cust+1) + dist_mat(cust+1, 1);  % depot→cust→depot
        return;
    end
    min_cost = inf;
    for i = 0:length(route)
        if i == 0
            prev = 0; next = route(1);
        elseif i == length(route)
            prev = route(end); next = 0;
        else
            prev = route(i); next = route(i+1);
        end
        original_dist = dist_mat(prev+1, next+1);
        new_dist = dist_mat(prev+1, cust+1) + dist_mat(cust+1, next+1);
        cost_add = new_dist - original_dist;
        if cost_add < min_cost
            min_cost = cost_add;
        end
    end
    cost = min_cost;
end
四、代码说明与扩展
  1. 测试数据：示例使用5个客户（可替换为Solomon数据集或自定义数据）。
  2. 核心操作 ： 交换（Swap） ：随机交换两个客户的位置，探索新路径。 插入（Insert） ：将客户从一个路径移到另一个路径，优化负载均衡。 变异（Mutation）：反转路径片段，跳出局部最优。
  3. 约束处理 ：通过repair_capacity函数确保容量约束，通过setdiff确保无遗漏客户。
五、结果分析
  • 收敛曲线：迭代过程中总距离逐渐减小，最终趋于稳定（示例收敛到约200单位距离）。
  • 路径图：显示每辆车的行驶路线，depot用红色圆圈表示，客户点用蓝色圆圈表示。

参考代码 粒子群算法求解标准VRP问题 www.youwenfan.com/contentcsm/82797.html

六、扩展优化
  1. 局部搜索：加入2-opt或3-opt算法优化每条路径，提升解质量。
  2. 自适应参数 ：动态调整惯性权重和学习因子（如w随迭代次数非线性递减）。
  3. 多目标优化：同时最小化总距离和车辆数量（ Pareto 前沿）。
相关推荐
Ayanami_Reii1 小时前
进阶数据结构应用-SPOJ 3267 D-query
数据结构·算法·线段树·主席树·持久化线段树
dangdang___go1 小时前
文件操作c语言
c语言·开发语言
塔能物联运维1 小时前
设备断网时数据丢失，后来启用本地缓存+异步重传队列
java·开发语言·缓存
天涯路s2 小时前
qt怎么自定义日志
开发语言·qt
Evand J2 小时前
【自适应IMM】MATLAB编写的创新多模型，基于CA/CT双模型和观测自适应。二维平面目标位置估计，带误差统计特性输出，附代码下载链接
开发语言·matlab·ekf·imm·交互式多模型
我命由我123452 小时前
微信小程序 - scroll-view 的一些要点（scroll-view 需要设置滚动方向、scroll-view 需要设置高度）
开发语言·前端·javascript·微信小程序·小程序·前端框架·js
7哥♡ۣۖᝰꫛꫀꪝۣℋ2 小时前
Spring IoC&DI
java·开发语言·mysql
wadesir2 小时前
Go语言反射之结构体的深比较（详解reflect.DeepEqual在结构体比较中的应用）
开发语言·后端·golang
guygg882 小时前
基于全变差的压缩感知视频图像重构算法
算法·重构·音视频
热门推荐
01GitHub 镜像站点02React CVE-2025-55182漏洞排查与修复指南03【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05UV安装并设置国内源06BongoCat - 跨平台键盘猫动画工具07智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践08本地部署阿里最新开源的Z-Image09Linux下V2Ray安装配置指南10论文阅读 - 深度学习端到端解决库存管理问题 - 有限时间范围内的多周期补货问题（Management Science）