0013机器学习聚类算法(无监督算法)
- 一、聚类算法
- 二、K均值聚类(K-means)
-
- [1.1 编程实现K-means](#1.1 编程实现K-means)
- [2.2 调库实现K-means](#2.2 调库实现K-means)
- [3.3 鸢尾花数据K-means聚类](#3.3 鸢尾花数据K-means聚类)
- [4.4 K-means缺点](#4.4 K-means缺点)
- 三、肘方法
- 四、K-means++
- 五、K-means||
- [六、Mini Batch K-Means*](#六、Mini Batch K-Means*)
- 七、K-Mediods聚类
- 八、评估方法
- 九、DBSCAN聚类算法
一、聚类算法
- 聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数 据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
- 聚类算法是一种无监督算法,无监督学习(Unsupervised Learning)是指在 无标注训练数据(即数据仅包含输入特征X,无对应的输出标签 y)的情况下,通过算法自动挖掘数据内部的结构、分布、关联或异常模式的学习方法。
二、K均值聚类(K-means)
-
虽然其思想能够追溯到1957年的Hugo Steinhaus,术语"k-均值"于1967年才被James
MacQueen首次使用。标准算法则是在1957年被Stuart Lloyd作为一种脉冲码调制的技术所提出,但直到1982年才被贝尔实验室公开出版。在1965年,E.W.Forgy发表了本质上相同的方法,所以这一算法有时被称为Lloyd-Forgy方法。更高效的版本则被Hartigan and Wong提出 (1975/1979)
-
K-Means算法是无监督的聚类算法,算法简单,聚类效果好,即使是在巨大的数据集上也非常容易部署实施。正因为如此,它在很多领域都得到的成功的应用,如市场划分、机器视觉、地质统计学、天文学和农业等。K-Means算法有大量的变体,包括初始化优化K-Means++以及大数据应用背景下的k-means||和Mini Batch K-Mean
-
直观理解
-
Kmeans聚类的可视化演示:https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
1.1 编程实现K-means
python
import numpy as np
import sys
if __name__ == '__main__':
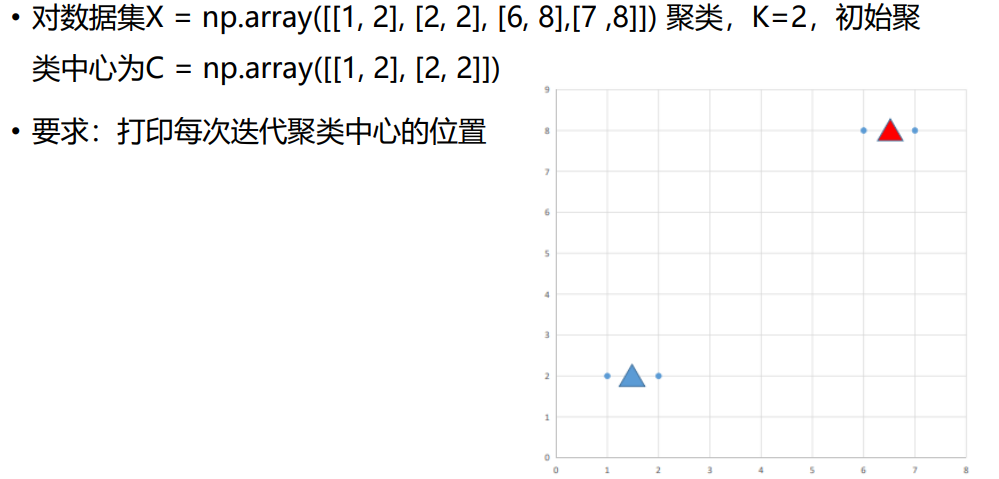
X = np.array([[1.0, 2.0], [2.0, 2.0], [6.0, 8.0], [7.0, 8.0]])
C = np.array([[1.0, 2.0], [2.0, 2.0]])
iters = 5 ###迭代次数
while iters > 0:
###计算每个样本到每个聚类中心的距离
A = []
for c in C: ##聚类中心
a = np.sqrt(np.sum((X - c) ** 2, axis=1))
A.append(a)
A = np.array(A)
print(A)
###将样本分配的所属的聚类中心(获取最小值的下标)
minidx = np.argmin(A, axis=0)
print(minidx)
###获取每个簇的样本
for i in range(len(C)):
a = X[minidx == i] ###每个簇的样本
print('a\n', a)
C[i] = np.mean(a, axis=0) ###更新我们的聚类中心
# print(C[i])
print("C\n", C)
# todo: 就是C不再更新时要停止,停止
print('---------------------------------')
iters -= 1
# todo:封装成类【伪代码】,加上就是C不再更新停止2.2 调库实现K-means
python
import numpy as np #
from sklearn.cluster import KMeans
import warnings
warnings.filterwarnings("ignore")
def demo1():
X = np.array([[1, 2], [2, 2], [6, 8], [7, 8]])
kmeans = KMeans(n_clusters=2, n_init='auto')
kmeans.fit(X)
print(kmeans.cluster_centers_) ##簇中心
print(kmeans.labels_) ###簇的标签
def demo2():
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs # 生成数据函数
from sklearn import metrics
#解决中文乱码
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
n_samples = 1500
X, y = make_blobs(n_samples=n_samples, centers=4, random_state=170)
X = StandardScaler().fit_transform(X) # 标准化
kmeans = KMeans(n_clusters=4, n_init='auto', random_state=170)
kmeans.fit(X)
# 反映同类样本类内平均距离尽可能小,类间距离尽可能大的指标。取值范围在[-1,1]之间,越大越好
labels = kmeans.labels_
pgjg1 = metrics.silhouette_score(X, labels, metric='euclidean') # 轮廓系数,取值范围从-1到1
print('聚类结果的轮廓系数=', pgjg1)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c='r')
plt.title("聚类前数据图")
plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title("聚类后数据图")
plt.show()
if __name__ == '__main__':
demo1()
# demo2()3.3 鸢尾花数据K-means聚类
python
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import warnings
warnings.filterwarnings("ignore")
datas = pd.read_csv('data/iris.data', sep=",", header=None)
# print(datas.head())
X = datas.iloc[:, :-1]
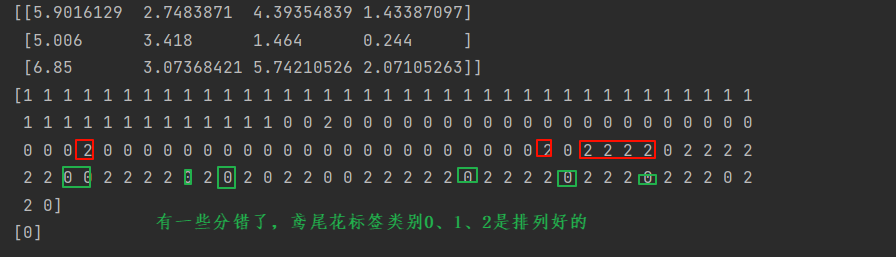
clf = KMeans(n_clusters=3,n_init='auto')
clf.fit(X)
print(clf.cluster_centers_)
print(clf.labels_)
pre = clf.predict(X.iloc[[-1],:])
print(pre)运行结果:
4.4 K-means缺点
- 缺点一:聚类中心的个数K需要事先给定,但在实际中K值的选定是非常困难的, 很多时候我们并不知道给定的数据集应该聚成多少个类别才最合适
- 缺点二:k-means算法需要随机地确定初始聚类中心,不同的初始聚类中心可能导致完全不同的聚类结果,有可能导致算法收敛很慢甚至出现聚类出错的情况
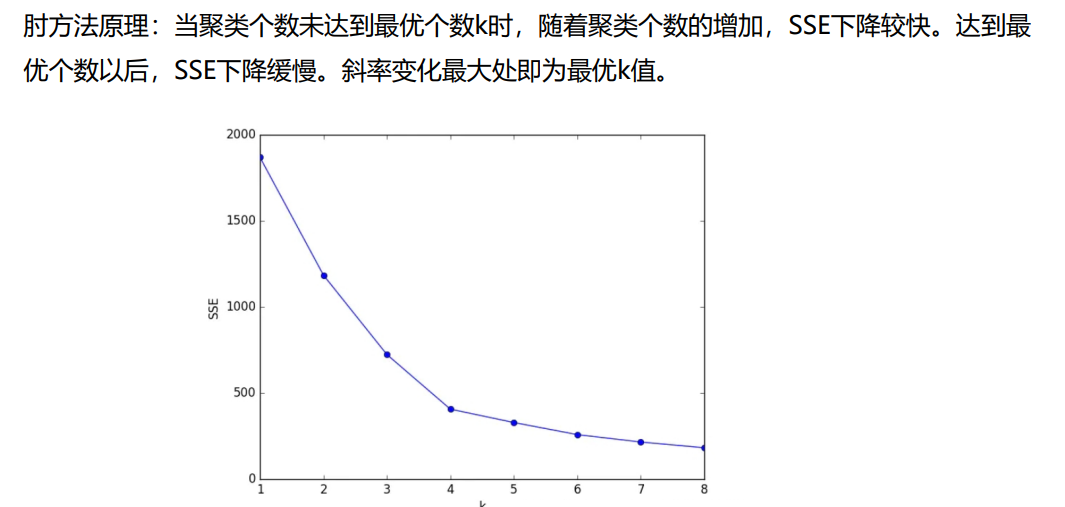
- 针对第一个缺点:很难在k-means算法以及其改进算法中解决,一般来说,我们会根据对数据的先验经验选择一个合适的k值,如果没有什么先验知识,则可以通过 "肘方法"选择一个合适的k值
- 针对第二个缺点:可以通过k-means++算法来解决
三、肘方法

代码实现:
python
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.metrics import silhouette_score ###轮廓系数
import warnings
warnings.filterwarnings("ignore")
datas = pd.read_csv('data/iris.data', sep=",", header=None)
# print(datas.head())
X = datas.iloc[:, :-1]
sses = []
S = []
for K in range(2, 10):
kmeans = KMeans(n_clusters=K, init="k-means++", n_init=10)
kmeans.fit(X)
inertia = kmeans.inertia_
sses.append(inertia)
# labels = kmeans.labels_
# s = silhouette_score(X, labels)
# print(s*100)
# S.append(s)
plt.figure(num=1)
plt.plot(range(2, 10), sses)
# plt.figure(num=2)
# plt.plot(range(2, 10), S)
plt.show()运行结果:
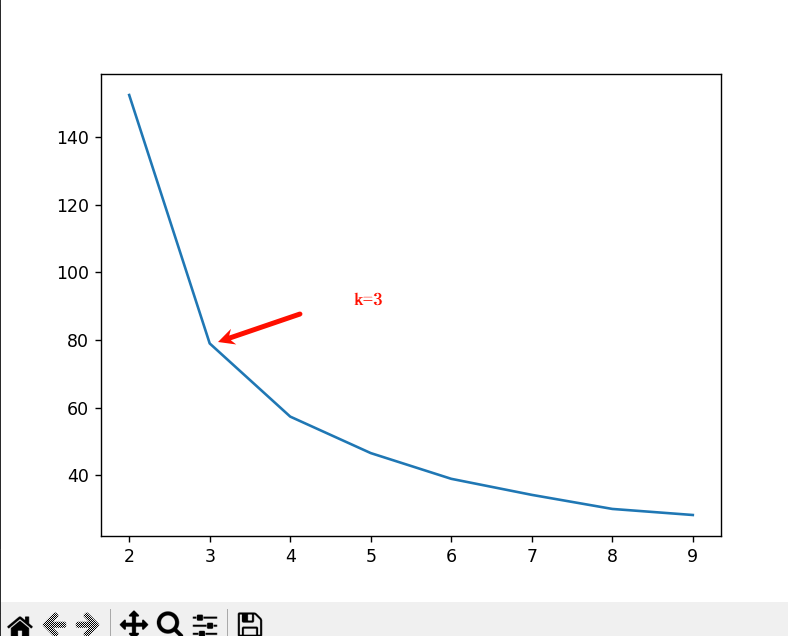
四、K-means++


五、K-means||


六、Mini Batch K-Means*

七、K-Mediods聚类
- K-means算法在迭代的过程中使用所有点的均值作为新的质点(中心点),如 果簇中存在异常点,将导致均值偏差比较严重。
- 解决方案:使用中位数可能比使用均值的方法更好,使用中位数的聚类方式 叫做K-Mediods聚类(K中值聚类)。
八、评估方法
1、肘方法

2、轮廓系数法

九、DBSCAN聚类算法



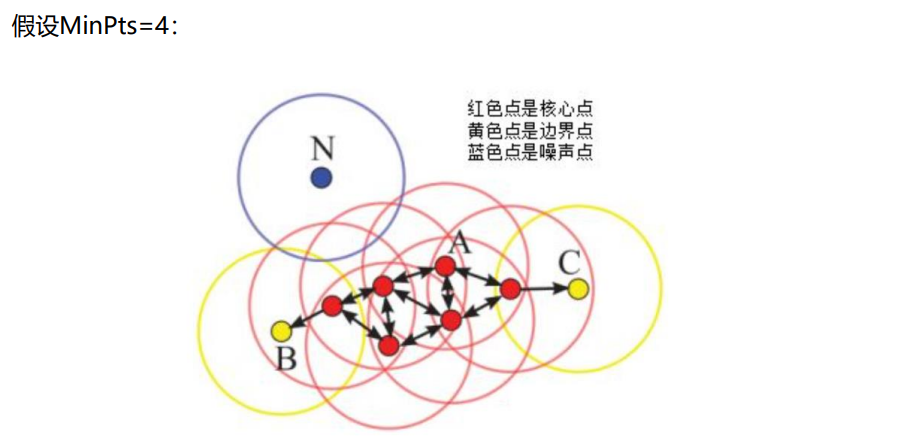

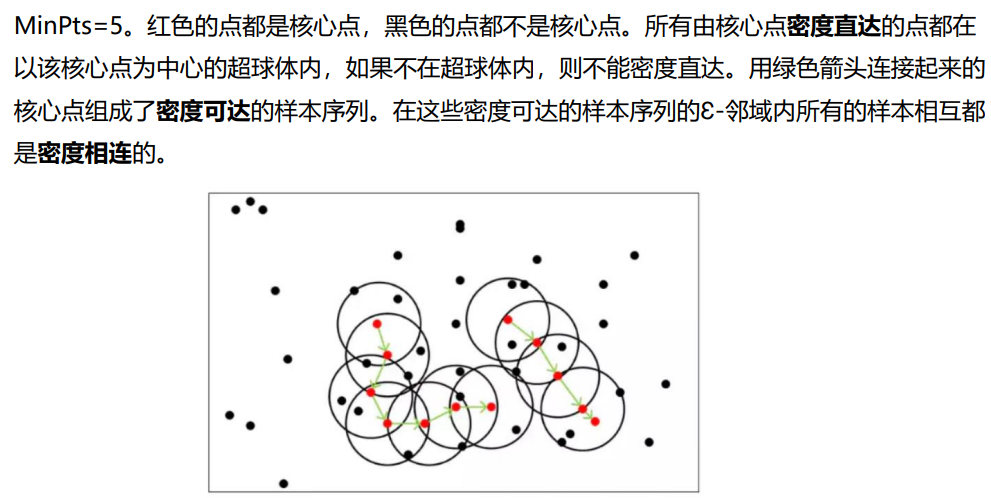
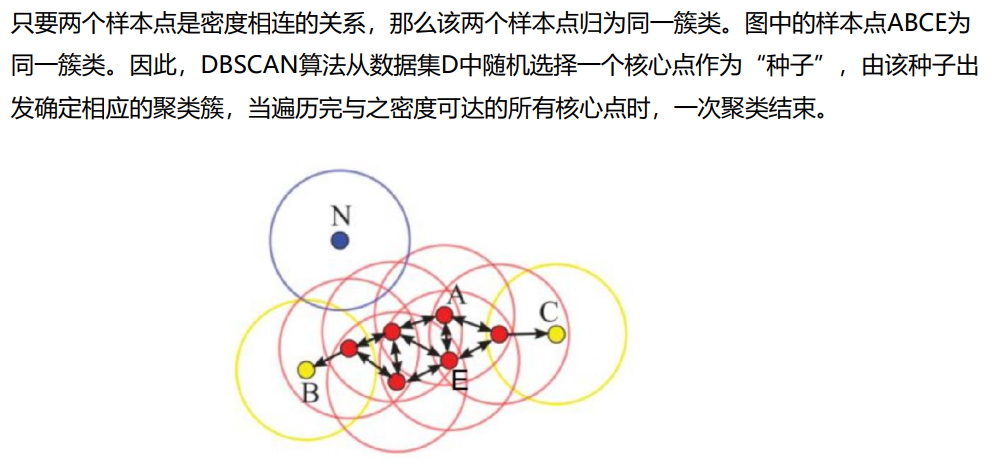
DBSCAN聚类的可视化演示:
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/