基于分数的扩散模型
(Score-Based Diffusion Model)
定义
高斯分布下:

噪声 ϵ 和 score 的关系
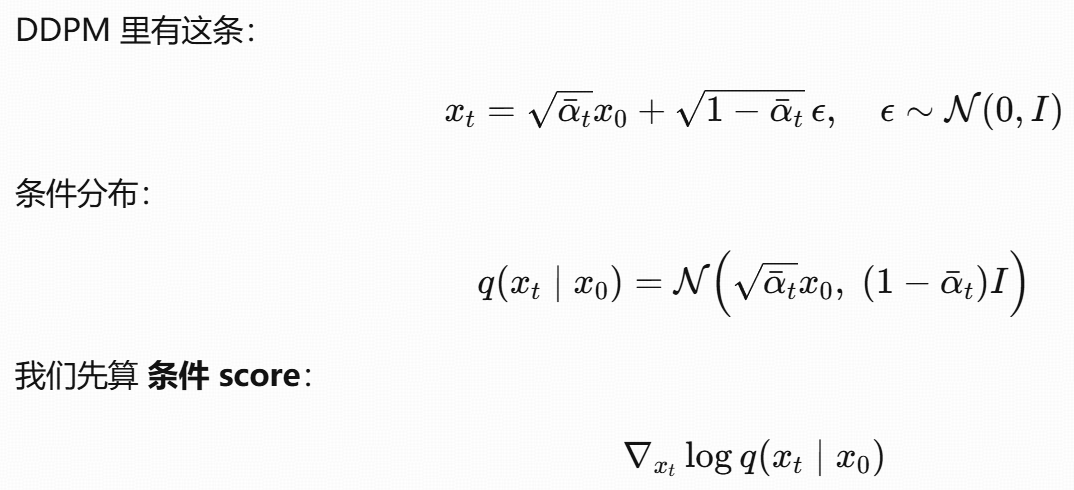
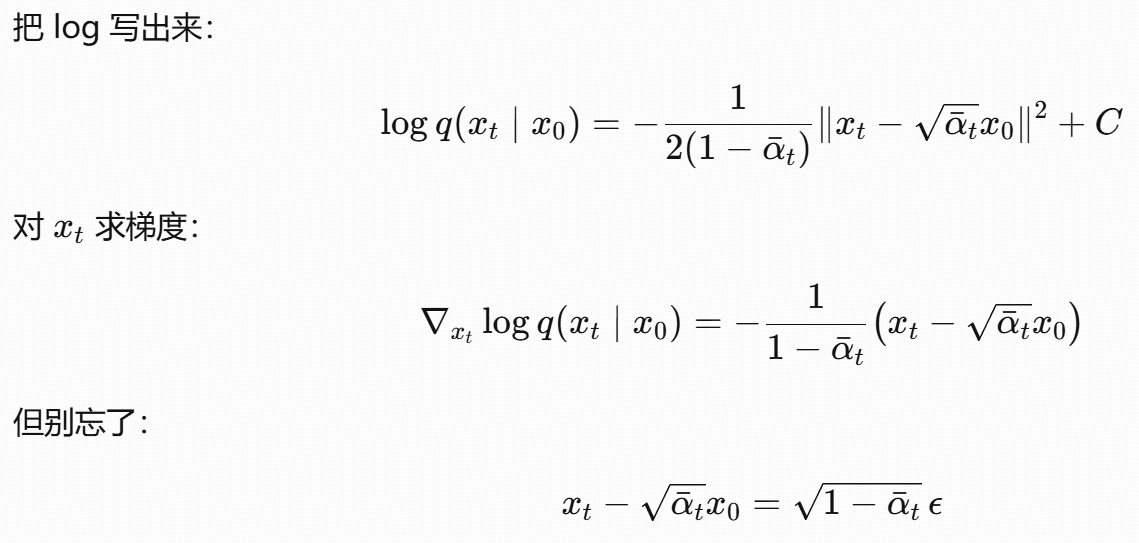


推导
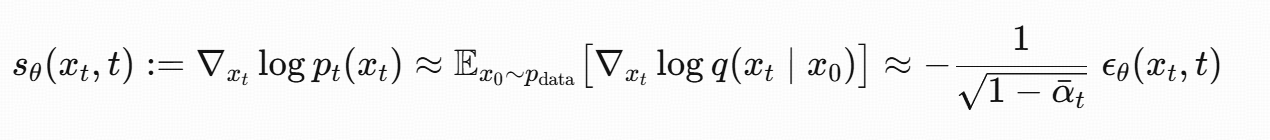
这个公式的本质是:用 "噪声预测网络" 间接学习 "分数函数",从而将 "难以计算的边缘分数" 转化为 "可训练的噪声预测任务",最终实现扩散模型的反向去噪过程。





时间步
扩散模型的核心是模拟 "噪声添加(前向过程)" 和 "噪声移除(反向过程)",时间步(timestep)是这个过程的核心索引:
- 离散扩散(如 LDM) :时间步是整数(如 0~1000),每个整数对应预定义的噪声调度参数(β/α/sigma),代表 "噪声添加的程度"(t=0 无噪声,t=1000 全噪声)。
- 连续扩散(如 Flow Matching/Flux) :时间步是浮点数(通常∈[0,1]),描述 "从纯噪声(t=0)到真实数据(t=1)" 的连续流场过程,无预定义离散调度表,依赖分布采样。
- 模型蒸馏:本质是 "将大模型(教师,多步)的能力压缩到小模型(学生,少步)",时间步需要适配 "学生步→教师步" 的映射。
LDM/Flow/ 蒸馏的采样差异,匹配这三种范式的底层逻辑:
-
LDM:离散时间步的均匀采样:其反向过程需要学习 "每个离散时间步的去噪函数"。为了让模型均匀学习所有噪声水平的去噪能力,必须均匀采样所有整数时间步(而非偏向某一区间)。
-
Flow 分支:连续时间步的分布采样:Flow-based Diffusion(如 Flux、Flow Matching)是连续扩散模型,核心是学习 "从噪声分布到数据分布的连续流场":
-
时间步 t∈[0,1]:t=0 对应纯噪声,t=1 对应真实数据;
-
时间步采样需贴合 "流场的优化目标":通常用logitnormal分布(而非均匀分布),因为 logitnormal 能让采样更偏向 t=0(高噪声)和 t=1(低噪声)区间,这两个区间是流场学习的关键。
-


| 分支 | 时间步类型 | 采样方式 | 底层原因 |
|---|---|---|---|
| LDM | 离散整数 | 均匀采样(分布式分组) | 离散扩散需覆盖所有噪声水平,分布式分组提升训练效率 |
| Flow | 连续浮点数 | 分布采样 + 调度偏移 | 连续流场需贴合 logitnormal 分布,偏移强化复杂样本的高噪声阶段学习 |
SDE与ODE
正/反向SDE


采样路线
有一条结论:
给定一条 SDE,其边缘分布 pt 也可以由一条确定性的 ODE 产生 ,这条 ODE 就是probability flow ODE。


区别
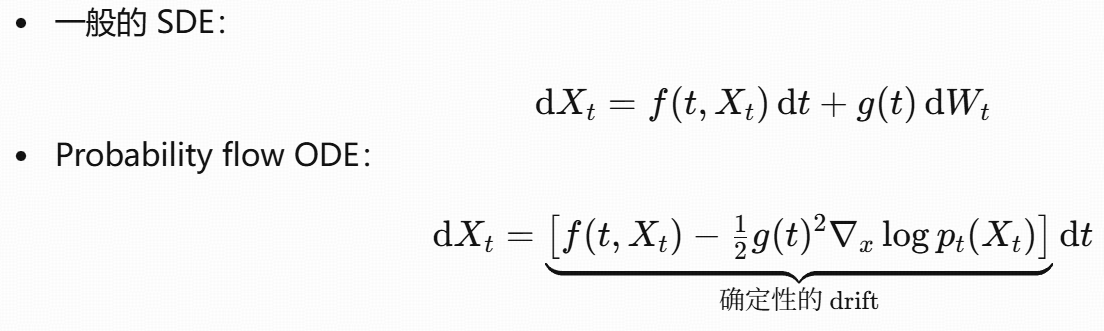

SDE/马尔可夫链
加噪 SDE(随机微分方程)和马尔可夫链是连续 - 离散的对应关系,核心是描述 "数据逐步加噪的过程":


flow matching
定义
不管是 diffusion 还是 flow matching,本质都是在干一件事:
从一个简单的先验分布(比如高斯)p0(x) 通过时间演化的动力系统,变成数据分布 p1(x)。
只不过:
-
Diffusion :用的是随机微分方程(SDE) / 反向 SDE / probability flow ODE ,学的是 score field。
-
Flow matching :直接用一个常微分方程(ODE) ,学的是速度场(vector field),把"该往哪边流"拟合出来。



训练目标:flow matching loss

总结:flow matching 就是直接学"点在这个时间点应该朝哪个方向流动",而不是学 score。
例子
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
# 超参数
dim = 2 # 数据维度(2D点:x坐标+sin(x)坐标)
num_samples = 1000 # 样本数量(生成1000个正弦曲线点)
num_steps = 50 # ODE数值求解的步数(欧拉法迭代次数)
lr = 1e-3 # 学习率(Adam优化器)
epochs = 5000 # 训练轮数
# 目标分布:正弦曲线上的点(x1坐标)
x1_samples = torch.rand(num_samples, 1) * 4 * torch.pi # 0到4π的随机x坐标
y1_samples = torch.sin(x1_samples) # y=sin(x),对应x的正弦值
target_data = torch.cat([x1_samples, y1_samples], dim=1) # 拼接成二维点 (x, sin(x))
# 噪声分布:高斯噪声(x0坐标)
noise_data = torch.randn(num_samples, dim) * 2 # 均值0、方差2的二维高斯噪声
class VectorField(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim + 1, 64), # 输入维度: x (2维点) + t (1维时间) = 3
nn.ReLU(), # 非线性激活
nn.Linear(64, dim) # 输出维度: 2维向量(对应每个点的速度/方向)
)
def forward(self, x, t):
# 拼接x(二维点)和t(时间),输入网络
return self.net(torch.cat([x, t], dim=1))
model = VectorField() # 初始化模型
optimizer = torch.optim.Adam(model.parameters(), lr=lr) # 定义优化器
for epoch in range(epochs):
# 随机采样噪声点和目标点(打乱顺序,避免数据顺序影响)
idx = torch.randperm(num_samples)
x0 = noise_data[idx] # 起点:噪声点(t=0)
x1 = target_data[idx] # 终点:正弦曲线点(t=1)
# 随机采样时间t(形状:(batch_size, 1)),t∈[0,1]
t = torch.rand(x0.size(0), 1)
# 线性插值生成中间点xt:xt = (1-t)*x0 + t*x1
xt = (1 - t) * x0 + t * x1
# 模型预测当前(xt, t)处的向量场
vt_pred = model(xt, t)
# 目标向量场:vt_target = x1 - x0(线性插值的导数,xt对t求导)
vt_target = x1 - x0
# 损失函数:MSE(预测向量场 vs 真实向量场)
loss = torch.mean((vt_pred - vt_target)**2)
# 反向传播+参数更新
optimizer.zero_grad() # 清空梯度
loss.backward() # 计算梯度
optimizer.step() # 更新参数
x = noise_data[0:1] # 选第一个噪声点作为初始点
trajectory = [x.detach().numpy()] # 记录轨迹的列表
# 数值求解ODE(欧拉法)
t = 0
delta_t = 1 / num_steps # 每步的时间增量(1/50)
with torch.no_grad(): # 禁用梯度计算(推理阶段)
for i in range(num_steps):
# 预测当前t时刻x点的向量场(速度)
vt = model(x, torch.tensor([[t]], dtype=torch.float32))
t += delta_t # 时间步进
x = x + vt * delta_t # 欧拉法更新位置:x(t+Δt) = x(t) + v(t)*Δt
trajectory.append(x.detach().numpy()) # 记录新位置
# 整理轨迹格式(去除冗余维度)
trajectory = torch.tensor(trajectory).squeeze()
# 打印最终点的x坐标(辅助验证)
print(trajectory[-1] / (torch.pi / 10 * 4))
# 绘制向量场和生成轨迹
plt.figure(figsize=(10, 5))
plt.scatter(target_data[:,0], target_data[:,1], c='blue', label='Target (sin(x))') # 目标分布(正弦)
plt.scatter(noise_data[:,0], noise_data[:,1], c='red', alpha=0.3, label='Noise') # 初始噪声
plt.plot(trajectory[:,0], trajectory[:,1], 'g-', linewidth=2, label='Generated Path') # 生成轨迹
plt.legend()
plt.title("Flow Matching: From Noise to Target Distribution")
plt.show()步骤 1:线性插值路径
定义从初始点 x0(t=0)到目标点 x1(t=1)的线性插值:xt=(1−t)x0+tx1
-
t=0 →
xt = x0(噪声点); -
t=1 →
xt = x1(正弦点); -
t∈(0,1) → 中间插值点。
步骤 2:目标向量场(真实速度)
对插值路径求导,得到真实的向量场:dt/dxt=x1−x0:这就是 vt_target 的由来 ------ 线性插值的速度是恒定的(与 t 无关)。
步骤 3:训练目标
让神经网络 model 学习预测这个真实向量场:
-
输入:插值点
xt+ 时间t; -
输出:预测的向量场
vt_pred; -
损失:MSE(
vt_pred - vt_target),即让模型的预测尽可能接近真实速度。
步骤 4:优化
用 Adam 优化器最小化损失,让模型学会在任意时间 t、任意插值点 xt 处,输出正确的移动方向 / 速度。

运行结果:
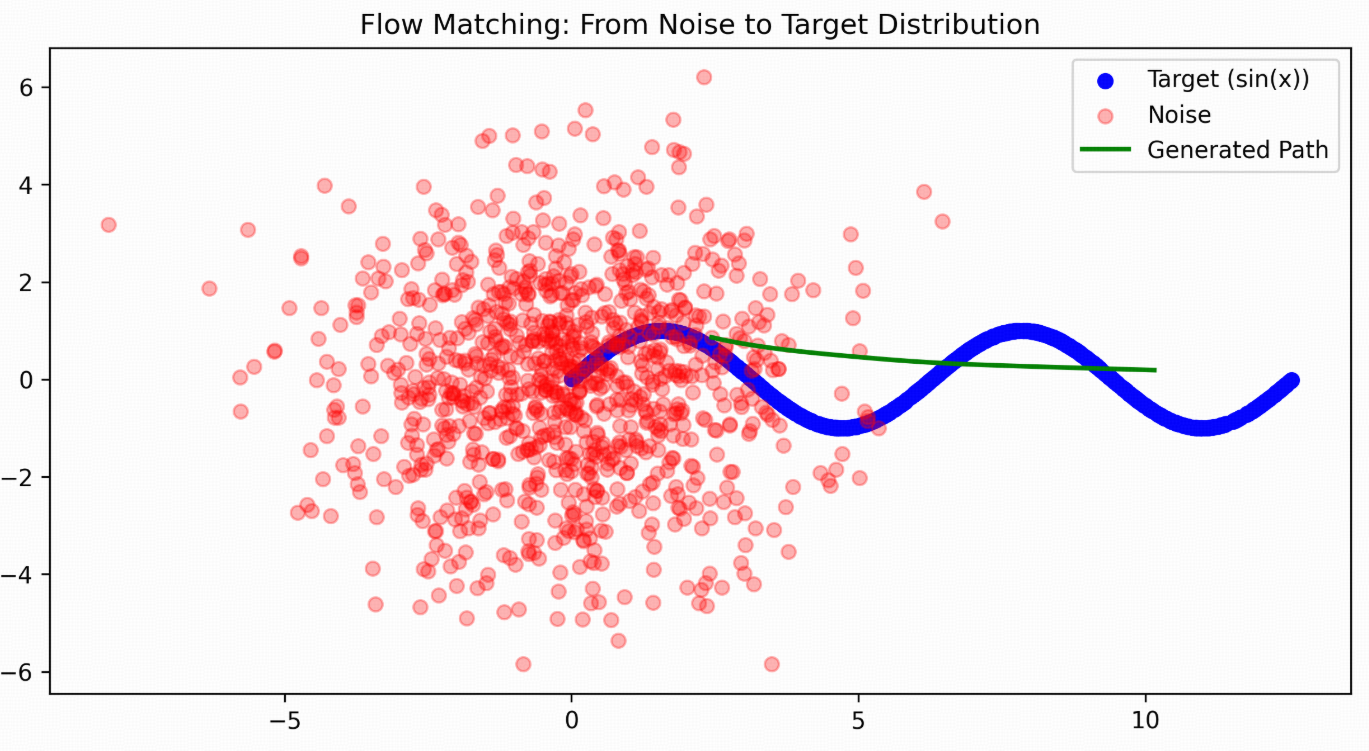
看起来好像不太准,尝试把epochs增大到50000后:可以看出来生成的路径是从一个随机noise点往target曲线上移动的。
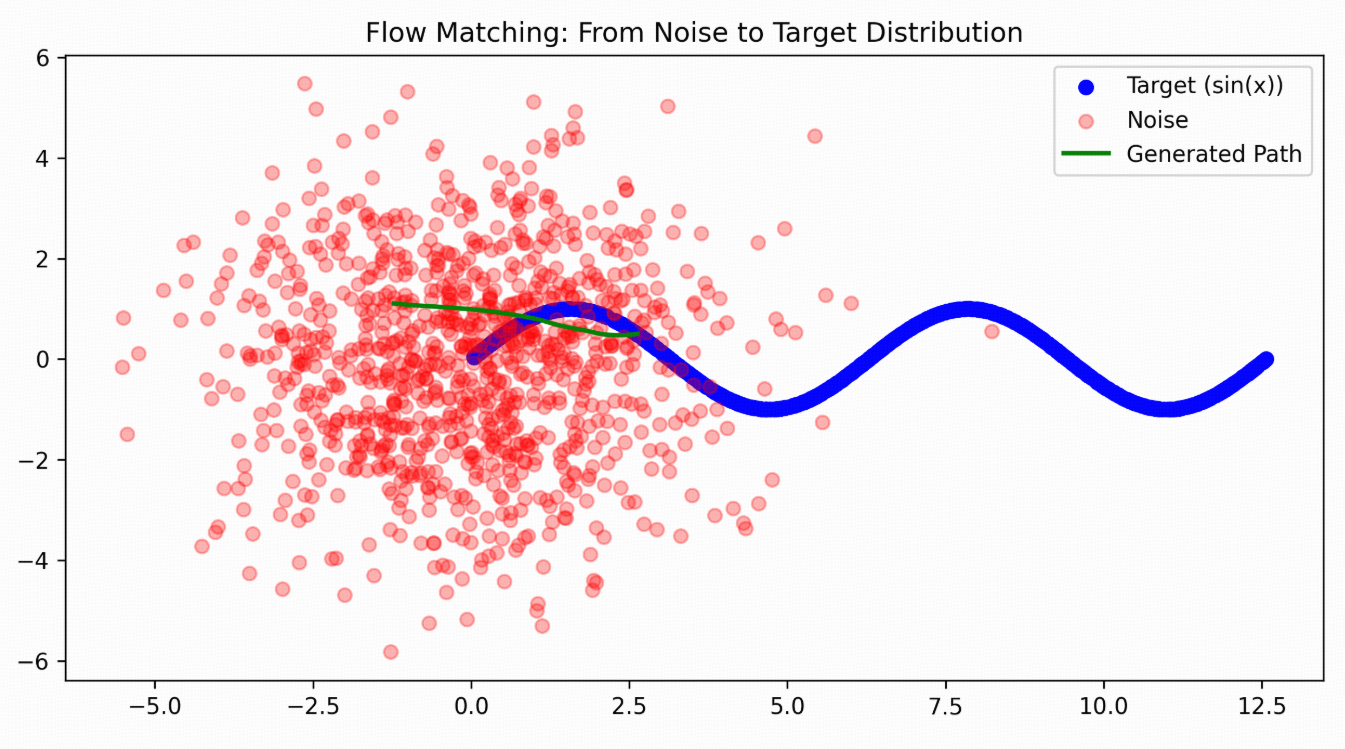
推理(采样)

连续性方程

某点的概率密度随时间变多/变少 = 从周围流入/流出的概率质量。写成数学就是:本地变化 + 净流出 = 0。
依据:总概率守恒,不会凭空生出概率,也不会凭空消失,只能流动。
对比diffusion






