【算法基础篇】（二十七）从记忆化搜索到动态规划：保姆级入门指南，带你吃透 DP 核心思想！

---

前言

在算法的世界里，有这样一个 "磨人的小妖精"------ 动态规划（Dynamic Programming，简称 DP）。它既是大厂面试的高频考点，也是算法竞赛中的 "得分利器"，却让无数初学者望而却步："听起来就好深奥""状态转移方程到底怎么推""为什么别人一眼就能想到，我却毫无头绪"？

其实动态规划没有那么玄乎！它就像一个聪明的 "记忆大师"，遇到重复的问题时，会把答案记下来，下次再遇到就直接复用，避免做无用功。今天这篇 5000 字长文，就从最基础的记忆化搜索开始，一步步带你走进动态规划的世界，用生动的例子、详细的代码拆解，让你彻底搞懂 DP 的核心逻辑，从此不再惧怕这类问题。下面就让我们正式开始吧！

---

一、为什么动态规划如此 "难入门"？

在正式学习之前，我们先聊聊为什么很多人觉得动态规划难。其实主要原因有三点：

1. 概念抽象，不像 "暴力搜索" 那样直观

动态规划的核心思想是**"分治 + 记忆化"**，但它不像暴力搜索那样，能直接看出 "一步步尝试所有可能" 的逻辑。它需要我们跳出具体的操作，站在 "状态" 的角度思考问题 ------ 什么是状态？如何表示状态？状态之间如何转移？这些抽象的概念，需要通过具体题目才能慢慢理解。

2. 题型多变，没有 "万能模板"

动态规划不是一种特定的算法，而是一种解决问题的思想。它的应用场景非常广泛：从简单的斐波那契数列，到复杂的背包问题、区间合并问题，再到字符串匹配问题，每种题型的状态设计和转移方程都不同。这意味着我们不能死记硬背模板，必须理解其本质。

3. 入门门槛高，需要 "思维跃迁"

很多算法（比如排序、搜索）入门时，只要掌握基本逻辑就能解决不少问题。但动态规划入门时，即使理解了概念，也可能面对题目无从下手。这是因为它需要我们具备 "拆分问题" 的能力 ------ 把复杂问题拆解成若干个重叠的子问题，再通过子问题的解推导出原问题的解。这种思维方式，需要通过大量练习才能培养。

不过大家不用慌！动态规划的学习遵循 "量变到质变" 的规律，只要坚持做几道题，就能逐渐找到感觉。接下来，我们就从最基础的 "记忆化搜索" 开始，一步步搭建动态规划的知识体系。

二、铺垫：什么是记忆化搜索？------ 动态规划的 "雏形"

在学习动态规划之前，我们先来看一个经典问题：斐波那契数列。这个问题是理解记忆化搜索和动态规划的最佳切入点。

2.1 斐波那契数列的 "暴力困境"

斐波那契数列的定义很简单：

• F(0) = 0，F(1) = 1
• 对于 n ≥ 2，F (n) = F (n-1) + F (n-2)

如果用暴力递归的方式实现，代码如下：

int fib(int n) {
    if (n == 0 || n == 1) return n;
    return fib(n-1) + fib(n-2);
}

看似简洁，但当 n 较大时（比如 n=30），程序的运行速度会变得非常慢。为什么？我们可以画出递归树来看看：

当计算 fib (5) 时，递归树是这样的：

fib(5)
├─ fib(4)
│  ├─ fib(3)
│  │  ├─ fib(2)
│  │  │  ├─ fib(1) → 1
│  │  │  └─ fib(0) → 0
│  │  └─ fib(1) → 1
│  └─ fib(2)
│     ├─ fib(1) → 1
│     └─ fib(0) → 0
└─ fib(3)
   ├─ fib(2)
   │  ├─ fib(1) → 1
   │  └─ fib(0) → 0
   └─ fib(1) → 1

我们发现，fib (3) 被计算了 2 次，fib (2) 被计算了 3 次，fib (1) 被计算了 5 次 ------ 大量的重复计算导致了效率低下。这种情况下，时间复杂度是 O (2ⁿ)，当 n=40 时，运算次数就会达到上亿次，程序几乎无法运行。

2.2 记忆化搜索：给递归 "加个备忘录"

既然问题出在 "重复计算" 上，那我们能不能把已经计算过的结果存起来，下次再遇到时直接取用？这就是 "记忆化搜索" 的核心思想。

我们可以用一个数组（相当于 "备忘录"）来存储已经计算过的斐波那契数。当调用 fib (n) 时，先检查备忘录里有没有存过 F (n)：

• 如果有，直接返回备忘录里的值；
• 如果没有，计算后把结果存入备忘录，再返回。

代码实现如下：

#include <iostream>
using namespace std;

const int N = 100;
int f[N]; // 备忘录数组，存储已经计算过的斐波那契数

int fib(int n) {
    // 先查备忘录，如果已经计算过，直接返回
    if (f[n] != -1) return f[n];
    // 递归出口
    if (n == 0 || n == 1) return f[n] = n;
    // 计算并存入备忘录
    f[n] = fib(n-1) + fib(n-2);
    return f[n];
}

int main() {
    // 初始化备忘录为-1，表示未计算
    memset(f, -1, sizeof f);
    int n;
    cin >> n;
    cout << fib(n) << endl;
    return 0;
}

这样改造后，递归树就变成了 "无重复" 的结构：每个 F (n) 只计算一次，计算后存入备忘录。此时时间复杂度从 O (2ⁿ) 降到了 O (n)，空间复杂度是 O (n)（用于存储备忘录和递归栈）。

2.3 记忆化搜索的本质：分治 + 缓存

记忆化搜索其实是 "分治思想" 和 "缓存机制" 的结合：

• 分治：把大问题（计算 F (n)）拆解成小问题（计算 F (n-1) 和 F (n-2)）；
• 缓存：用备忘录存储小问题的解，避免重复计算。

这正是动态规划的核心思想！可以说，记忆化搜索是动态规划的 "雏形"------ 它已经具备了动态规划的两个关键特征：重叠子问题 和最优子结构（对于斐波那契数列，虽然没有 "最优" 之说，但子问题的解可以直接复用）。

三、从记忆化搜索到动态规划：递归改递推

记忆化搜索虽然解决了重复计算的问题，但它本质上还是递归，可能会遇到栈溢出的问题（比如当 n=1e4 时，递归深度过深）。因此，我们需要把递归改成非递归的形式 ------ 递推，这就是动态规划的标准形式。

3.1 斐波那契数列的递推实现

我们再回顾一下斐波那契数列的定义：F (0)=0，F (1)=1，F (n)=F (n-1)+F (n-2)。

观察这个规律，我们发现：要计算 F (n)，只需要先计算 F (0)、F (1)，然后依次计算 F (2)、F (3)...... 直到 F (n)。这种 "从小到大" 的计算方式，就是递推。

代码实现如下：

#include <iostream>
using namespace std;

const int N = 100;
int f[N]; // f[i]表示第i个斐波那契数

int fib(int n) {
    // 初始化：边界条件
    f[0] = 0;
    f[1] = 1;
    // 递推：从左往右计算
    for (int i = 2; i <= n; i++) {
        f[i] = f[i-1] + f[i-2];
    }
    return f[n];
}

int main() {
    int n;
    cin >> n;
    cout << fib(n) << endl;
    return 0;
}

这个代码的逻辑非常清晰：

1. 初始化：先确定边界条件（F (0) 和 F (1)）；
2. 递推：按照递推公式，从左到右依次计算每个 F (i)；
3. 结果：f [n] 就是我们要求的答案。

此时，时间复杂度依然是 O (n)，空间复杂度是 O (n)。我们还可以进一步优化空间：因为计算 F (i) 只需要 F (i-1) 和 F (i-2) 两个值，不需要存储整个数组。可以用两个变量来替代数组：

int fib(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    int a = 0, b = 1;
    for (int i = 2; i <= n; i++) {
        int c = a + b;
        a = b;
        b = c;
    }
    return b;
}

优化后，空间复杂度降到了 O (1)，这就是动态规划的 "空间优化" 技巧 ------ 只保留必要的状态，丢弃无用的历史状态。

3.2 动态规划的核心概念：状态、转移、初始化

通过斐波那契数列的递推实现，我们可以引出动态规划的三个核心概念，这三个概念是解决所有 DP 问题的基础，必须牢牢掌握！

1. 状态表示（State Representation）

状态表示是动态规划的 "灵魂"，它回答了 "我们用什么来存储子问题的解"。在斐波那契数列中，我们用 f [i] 表示 "第 i 个斐波那契数"------ 这就是状态表示。

状态表示通常用数组（一维、二维甚至多维）来实现，数组的每个元素都对应一个 "子问题"。设计状态表示时，需要明确：

• 数组的维度：根据问题的复杂程度，选择一维、二维或多维数组；
• 数组元素的含义：必须清晰定义 f [i]（或f [i][j]）代表什么，这是后续推导转移方程的基础。

2. 状态转移方程（State Transition Equation）

状态转移方程是动态规划的 "骨架"，它回答了 "如何通过子问题的解推导出当前问题的解"。在斐波那契数列中，状态转移方程是 f [i] = f [i-1] + f [i-2]。

推导状态转移方程的关键是 "拆分问题"：找到当前状态和之前状态之间的逻辑关系。通常可以通过 "最后一步操作" 来拆分 ------ 比如 "要到达第 i 个位置，最后一步是从哪里来的？"。

3. 初始化（Initialization）

初始化是动态规划的 "地基"，它回答了 "子问题的边界条件是什么"。在斐波那契数列中，初始化是 f [0] = 0，f [1] = 1------ 这些是不需要通过转移方程就能直接确定的边界值。

初始化的核心是：确保所有通过转移方程计算的状态，其依赖的初始状态都是已知的。如果初始化错误，后续的计算都会出错。

4. 填表顺序（Filling Order）

填表顺序是动态规划的 "流程"，它回答了 "我们应该按什么顺序计算状态"。在斐波那契数列中，填表顺序是 "从左往右"------ 因为计算 f [i] 需要 f [i-1] 和 f [i-2]，而这两个状态在 i 之前已经计算过。

填表顺序的原则是：在计算当前状态之前，其依赖的所有状态都已经计算完成。如果顺序错误，就会出现 "用未计算的状态来推导当前状态" 的情况，导致结果错误。

5. 最终结果（Final Result）

最终结果是动态规划的 "答案"，它回答了 "我们要求的问题对应哪个状态"。在斐波那契数列中，最终结果是 f [n]。

有时候，最终结果可能不是某个单一状态，而是多个状态中的最大值、最小值或总和 ------ 这需要根据具体问题来确定。

3.3 动态规划与记忆化搜索的关系

看到这里，你可能会问：动态规划和记忆化搜索到底是什么关系？

简单来说：动态规划是记忆化搜索的 "递推实现"。它们的核心思想完全一致，都是 "存储子问题的解，避免重复计算"，但实现方式不同：

• 记忆化搜索 ：自上而下（Top-Down），从原问题出发，递归拆解成子问题，遇到未计算的子问题就计算并存储；
• 动态规划 ：自下而上（Bottom-Up），从子问题出发，依次计算出更大的子问题，最终得到原问题的解。

两者的对比可以用下表表示：

特性	记忆化搜索	动态规划
实现方式	递归	递推
计算顺序	自上而下	自下而上
空间复杂度	包含递归栈，可能较高	可优化，通常较低
适用场景	子问题稀疏时更高效	子问题密集时更高效
代码难度	思维直接，代码简洁	需设计状态和转移方程

在实际应用中，我们可以根据问题的特点选择合适的方式。但对于大多数 DP 问题，动态规划（递推）的效率更高，也更不容易出现栈溢出问题，因此是更推荐的实现方式。

四、动态规划入门实战：手把手教你解 "下楼梯" 问题

理论讲完了，现在我们来做一道实战题，巩固一下动态规划的核心概念。这道题是动态规划的入门经典题 ------ 下楼梯问题，难度适中，非常适合初学者。

题目链接：https://www.luogu.com.cn/problem/P10250

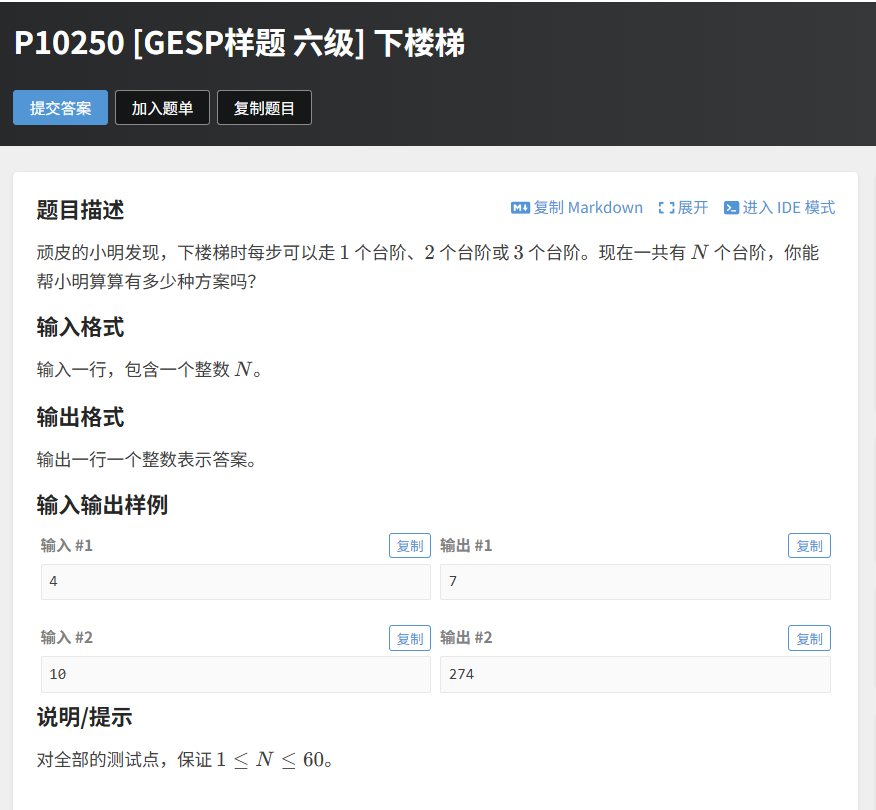
4.1 题目描述（洛谷 P10250）

小明下楼梯时，每步可以走 1 个、2 个或 3 个台阶。现在有 N 个台阶，请问小明有多少种不同的下楼梯方案？

输入：一个整数 N（1 ≤ N ≤ 60）

输出：一个整数，表示方案数

示例 1：输入：4 输出：7

示例 2：输入：10 输出：274

4.2 问题分析

首先，我们需要把这个实际问题转化为动态规划的模型，也就是明确 "状态表示、状态转移方程、初始化、填表顺序和最终结果"。

1. 状态表示

我们需要定义一个状态，来表示 "子问题的解"。这里的子问题是 "走到第 i 个台阶有多少种方案"。因此：

• 定义f [i]：走到第 i 个台阶的总方案数。

最终结果就是 f [N]------ 走到第 N 个台阶的方案数。

2. 状态转移方程

如何推导状态转移方程？我们可以从 "最后一步操作" 入手：

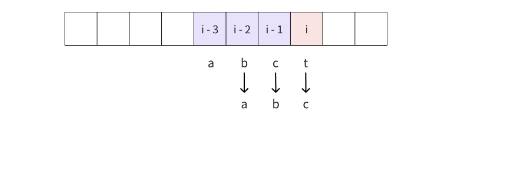
小明走到第 i 个台阶，最后一步可能有三种情况：

• 最后一步走了 1 个台阶：那么他之前在第 i-1 个台阶，方案数就是 f [i-1]；
• 最后一步走了 2 个台阶：那么他之前在第 i-2 个台阶，方案数就是 f [i-2]；
• 最后一步走了 3 个台阶：那么他之前在第 i-3 个台阶，方案数就是 f [i-3]。

因此，走到第 i 个台阶的总方案数，就是这三种情况的方案数之和：f [i] = f [i-1] + f [i-2] + f [i-3]

3. 初始化

我们需要确定边界条件，也就是不需要通过转移方程就能直接计算的状态：

• 当 i=1 时，只有 1 种方案（走 1 个台阶），所以 f [1] = 1；
• 当 i=2 时，有 2 种方案（走 1+1 个台阶，或直接走 2 个台阶），所以 f [2] = 2；
• 当 i=3 时，有 4 种方案（1+1+1、1+2、2+1、3），所以 f [3] = 4。

或者，我们也可以初始化 f [0] = 1（表示 "在第 0 个台阶" 有 1 种方案，即原地不动），这样：

• f [1] = f [0] + f [-1] + f [-2] → 这里需要注意 i-1、i-2、i-3 不能小于 0，所以实际计算时要确保边界合法。
• 不过更简单的方式是直接初始化前 3 个状态，避免处理负数。

4. 填表顺序

因为 f [i] 依赖于 f [i-1]、f [i-2]、f [i-3]，所以填表顺序是**"从左往右"**，从 i=4 开始，依次计算到 i=N。

4.3 代码实现

根据上面的分析，我们可以写出代码：

版本一：基础版（数组实现）

#include <iostream>
using namespace std;

typedef long long LL; // 因为N最大为60，结果可能很大，用long long防止溢出
const int N = 65;
LL f[N]; // f[i]表示走到第i个台阶的方案数

int main() {
    int n;
    cin >> n;
    // 初始化
    f[1] = 1;
    f[2] = 2;
    f[3] = 4;
    // 递推计算
    for (int i = 4; i <= n; i++) {
        f[i] = f[i-1] + f[i-2] + f[i-3];
    }
    cout << f[n] << endl;
    return 0;
}

版本二：空间优化版

观察到 f [i] 只依赖于前 3 个状态，我们可以用 3 个变量来替代数组，优化空间复杂度：

#include <iostream>
using namespace std;

typedef long long LL;

int main() {
    int n;
    cin >> n;
    // 初始化：a=f[1], b=f[2], c=f[3]
    LL a = 1, b = 2, c = 4;
    if (n == 1) cout << a << endl;
    else if (n == 2) cout << b << endl;
    else if (n == 3) cout << c << endl;
    else {
        for (int i = 4; i <= n; i++) {
            LL t = a + b + c;
            a = b;
            b = c;
            c = t;
        }
        cout << c << endl;
    }
    return 0;
}

4.4 代码测试

我们用示例输入来测试代码：

• 输入 4：输出 7（正确，因为 4 个台阶的方案有 1+1+1+1、1+1+2、1+2+1、2+1+1、2+2、1+3、3+1，共 7 种）；
• 输入 10：输出 274（正确，符合题目示例）。

通过这道题，我们可以发现：动态规划的解题流程是固定的 ------ 先定义状态，再推导转移方程，然后初始化边界，最后按顺序填表。只要掌握了这个流程，就能解决大多数基础 DP 问题。

五、动态规划的关键思想：重叠子问题与最优子结构

在学习更多 DP 问题之前，我们需要深入理解动态规划的两个核心特性：重叠子问题 和最优子结构。这两个特性是判断一个问题是否适合用动态规划解决的关键。

5.1 重叠子问题（Overlapping Subproblems）

重叠子问题是指：原问题可以拆解成若干个小问题，而这些小问题之间存在重复 ------ 即同一个子问题会被多次计算。

比如在斐波那契数列中，计算 f (5) 需要 f (4) 和 f (3)，计算 f (4) 又需要 f (3) 和 f (2)，f (3) 被重复计算了两次 ------ 这就是重叠子问题。

动态规划通过 "存储子问题的解"（比如用数组 f 存储），让每个子问题只计算一次，从而避免了重复计算，提高了效率。这也是动态规划与分治算法的本质区别：分治算法的子问题是相互独立的，没有重叠，因此不需要存储子问题的解；而动态规划的子问题是重叠的，必须通过存储来避免重复计算。

5.2 最优子结构（Optimal Substructure）

最优子结构是指：原问题的最优解包含了子问题的最优解。也就是说，我们可以通过子问题的最优解，推导出原问题的最优解。

这里的 "最优" 是广义的，不仅指 "最大值""最小值"，也包括 "方案数""可行性" 等。比如：

• 在下楼梯问题中，走到第 i 个台阶的方案数（原问题），是走到第 i-1、i-2、i-3 个台阶的方案数（子问题）之和 ------ 子问题的解直接构成了原问题的解；
• 在后续的 "最大子段和" 问题中，以第 i 个元素为结尾的最大子段和（原问题），要么是第 i 个元素本身，要么是第 i 个元素加上以第 i-1 个元素为结尾的最大子段和（子问题）------ 子问题的最优解推导了原问题的最优解。

**最优子结构是状态转移方程的基础。**如果一个问题不具备最优子结构，就无法通过子问题的解推导出原问题的解，也就不能用动态规划解决。

5.3 如何判断一个问题是否适合用动态规划？

只要一个问题满足以下两个条件，就可以考虑用动态规划解决：

1. 存在重叠子问题：子问题之间有重复，需要存储解来避免重复计算；
2. 具备最优子结构：原问题的解可以通过子问题的解推导得出。

比如：

• 斐波那契数列：满足重叠子问题和最优子结构，适合用 DP；
• 下楼梯问题：满足重叠子问题和最优子结构，适合用 DP；
• 归并排序：子问题相互独立（没有重叠），不适合用 DP；
• 最长公共子序列（LCS）：满足重叠子问题和最优子结构，适合用 DP。

六、动态规划入门必做的基础题（含详细解析）

为了让大家更好地掌握动态规划的解题流程，这里再推荐1道入门必做的基础题------数字三角形。

题目链接：https://www.luogu.com.cn/problem/P1216

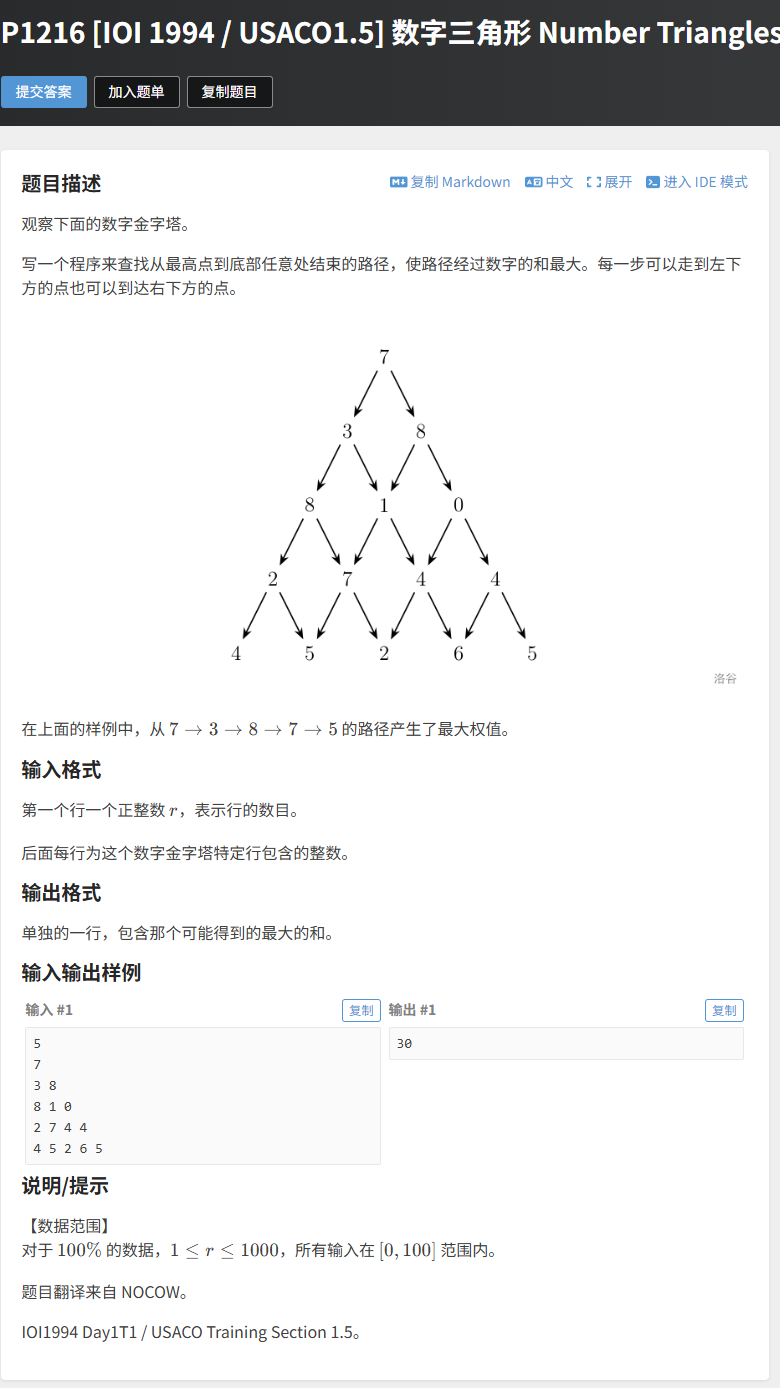
6.1 题目描述

观察数字金字塔，从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点或右下方的点。

输入：

• 第一行：整数 r（1 ≤ r ≤ 1000），表示行数；
• 接下来 r 行：第 i 行有 i 个整数（0 ≤ 数字 ≤ 100）。

示例：输入：573 88 1 02 7 4 44 5 2 6 5 输出：30（路径：7→3→8→7→5）

问题分析

1. 状态表示 ：定义**f [i][j]**为 "从顶部走到第 i 行第 j 列的最大和"（注意：行和列从 1 开始计数）。
2. 状态转移方程 ：第 i 行第 j 列的元素，只能从第 i-1 行第 j 列（左上方）或第 i-1 行第 j-1 列（右上方）走来。因此：f [i][j] = max (f [i-1][j], f [i-1][j-1]) + a [i][j]
3. 初始化 ：第一行只有一个元素，f [1][1] = a [1][1]。
4. 填表顺序：从上往下，每行从左往右（因为 f [i][j] 依赖 f [i-1][j] 和 f [i-1][j-1]）。
5. 最终结果 ：第 r 行所有f [r][j]中的最大值（因为可以从底部任意位置结束）。

代码实现

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int a[N][N], f[N][N];

int main() {
    int r;
    cin >> r;
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> a[i][j];
        }
    }
    // 初始化
    f[1][1] = a[1][1];
    // 递推计算
    for (int i = 2; i <= r; i++) {
        for (int j = 1; j <= i; j++) {
            f[i][j] = max(f[i-1][j], f[i-1][j-1]) + a[i][j];
        }
    }
    // 找第r行的最大值
    int max_sum = 0;
    for (int j = 1; j <= r; j++) {
        max_sum = max(max_sum, f[r][j]);
    }
    cout << max_sum << endl;
    return 0;
}

空间优化

由于f [i][j] 只依赖第 i-1 行的状态，我们可以用一维数组来优化空间。但需要注意：如果从左往右填表，会覆盖掉 f [j-1]（因为 f [j] 需要 f [j-1] 的值），因此需要从右往左填表。

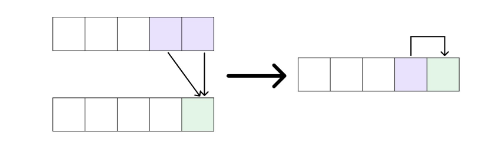
优化后的代码：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int a[N][N], f[N];

int main() {
    int r;
    cin >> r;
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> a[i][j];
        }
    }
    // 初始化
    f[1] = a[1][1];
    // 递推计算：每行从右往左
    for (int i = 2; i <= r; i++) {
        for (int j = i; j >= 1; j--) {
            f[j] = max(f[j], f[j-1]) + a[i][j];
        }
    }
    // 找最大值
    int max_sum = 0;
    for (int j = 1; j <= r; j++) {
        max_sum = max(max_sum, f[j]);
    }
    cout << max_sum << endl;
    return 0;
}

七、动态规划学习技巧与避坑指南

7.1 学习技巧

1. 从基础题入手，不要急于挑战难题：动态规划的思维需要慢慢培养，建议先做 10-20 道基础题（比如本文中的斐波那契、下楼梯、最大子段和、数字三角形等），掌握状态设计和转移方程推导的基本方法，再逐步挑战背包、区间 DP 等复杂问题。
2. 多画图，可视化状态转移：对于复杂问题（比如二维 DP），可以画出 DP 表，标注出状态之间的转移关系，这样能更直观地理解转移方程。
3. 总结题型，归纳套路：动态规划的题型虽然多，但很多问题都有相似的套路（比如线性 DP、背包 DP、区间 DP）。做完一道题后，要总结它的状态设计方式和转移方程推导思路，形成自己的 "题型库"。
4. 先暴力，再优化：遇到一道新的 DP 问题，先不要急于设计最优的状态表示，而是先思考暴力解法，然后分析暴力解法中的重复计算，再通过记忆化搜索或动态规划来优化。
5. 多写代码，动手实践：动态规划的理解离不开代码实现。每道题都要亲手写代码，调试过程中能发现很多思维漏洞（比如初始化错误、填表顺序错误）。

7.2 常见坑点

1. 状态表示不清晰：这是最常见的错误。如果状态表示模糊，后续的转移方程和初始化都会出错。解决方法：在写代码前，用文字明确写出 f [i]（或 f [i][j]）的含义，确保自己完全理解。
2. 转移方程推导错误：比如遗漏了某些转移情况（如下楼梯问题中忘记考虑走 3 个台阶的情况），或者逻辑错误（如把 "+" 写成 "*"）。解决方法：通过 "最后一步操作" 来拆分问题，确保覆盖所有可能的转移路径。
3. 初始化错误：边界条件设置错误，导致后续计算出错。解决方法：仔细分析问题的边界情况，确保初始化的状态是正确的。
4. 填表顺序错误：导致计算当前状态时，依赖的状态还未计算。解决方法：明确每个状态依赖哪些之前的状态，确保填表顺序满足 "依赖先于当前"。
5. 数据溢出：比如斐波那契数列、下楼梯问题中，当 n 较大时，结果会超出 int 范围。解决方法：根据题目数据范围，选择合适的数据类型（如 long long）。
6. 空间未优化：对于大规模问题（如 n=1e5），使用二维数组会导致内存超限。解决方法：观察状态依赖，尽量用一维数组或变量替代多维数组。

---

总结

动态规划看似复杂，但核心思想其实很简单：把复杂的原问题，拆解成若干个重叠的子问题，通过存储子问题的解，避免重复计算，最终推导出原问题的解。

学习动态规划的过程，就是培养 "拆分问题" 和 "抽象状态" 的能力。从记忆化搜索到递推实现，从一维 DP 到二维 DP，每一步都是思维的跃迁。但只要坚持 "理解概念→做基础题→总结套路→挑战难题" 的步骤，就能慢慢掌握动态规划。

最后，送给大家一句话：动态规划没有捷径，唯有多思考、多练习。当你做完 50 道甚至更多 DP 题后，会发现曾经让你头疼的问题，都变得豁然开朗。加油，祝你在算法的道路上越走越远！