5. 定积分与面积
- "定积分"不仅是数学工具,也是物理、统计、机器学习、概率、工程等领域的核心概念。
text
5.1 "积分 = 面积"的最核心直觉
5.2 用矩形逼近面积(Riemann 和)
5.3 定积分符号(∫)为什么长这样?
5.4 Python 代码模拟积分(数值积分)
5.5 积分的数学定义(通俗版)
5.6 定积分的性质
5.7 本节练习5.1 积分的最核心直觉:面积 = 无限小面积的累加
- 假设你有一个曲线下的面积:Area=面积Area=面积Area=面积
- 比如 f(x)=x² 在 x=0 到 x=2 之间的面积(等下用 Python 画)
- 直觉上我们想算曲线下的面积,宽度是 dx,高度是 f(x),无穷多个小矩形加起来
- 于是就有:
面积=∑f(x)dx\text{面积}=\sum f(x)dx面积=∑f(x)dx - 当 dx 很小,很小,很小......趋向于 0:
∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx
5.2 用 Riemann 和逼近面积(概念非常重要)
- 代码模拟过程:
python
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2
a, b = 0, 2
N = 20 # 分成20个矩形
xs = np.linspace(a, b, N+1)
# 左端点 Riemann 和
area = 0
for i in range(N):
xi = xs[i]
area += f(xi) * (b-a)/N
print("近似面积 =", area)近似面积 = 2.47- 面积随着 N 增大越来越准确:
text
N=20 → 面积 ≈ 2.63
N=100 → 面积 ≈ 2.666...
N=1000 → 面积 ≈ 2.666666...- 而真实面积是:
∫02x2dx=83=2.6‾\int_0^2x^2dx=\frac{8}{3}=2.\overline{6}∫02x2dx=38=2.6 - 完美验证积分 = 无限多个矩形的极限和
5.3 定积分符号长这样 ∫ 的原因
- 积分符号 ∫ 其实来自 拉长了的 S
- S = sum(和,求和)
- ∫ = 无限多小量的和(sum)
5.4 Python 数值积分
- 使用 NumPy 做简单数值积分(梯形法):
python
def numerical_integral(f, a, b, N=100000):
xs = np.linspace(a, b, N)
dx = (b - a) / N
return np.sum(f(xs) * dx)
print(numerical_integral(lambda x: x**2, 0, 2))2.66668000013333465.5 定积分的数学定义
-
正式定义(简单理解):
∫abf(x)dx=limN→∞∑i=1Nf(xi)Δx\int_a^bf(x)dx=\lim_{N\to\infty}\sum_{i=1}^Nf(x_i)\Delta x∫abf(x)dx=N→∞limi=1∑Nf(xi)Δx -
把区间切成很多小段,每段宽度 dx
-
用矩形逼近面积
-
全部加起来
-
小段越小 → 越准确
-
极限就是积分的值
5.6 定积分的性质
- 负面积也要加(位于 x 轴下方的部分是负值)
- 如果区间翻转,积分符号会变号:
∫baf(x)dx=−∫abf(x)dx\int_b^af(x) dx = -\int_a^bf(x) dx∫baf(x)dx=−∫abf(x)dx - 如果 a=b,面积为 0
- 分段积分可加和:
∫acf(x)dx+∫cbf(x)dx=∫abf(x)dx\int_a^c f(x)dx+\int_c^b f(x)dx=\int_a^b f(x)dx∫acf(x)dx+∫cbf(x)dx=∫abf(x)dx
5.7 本节练习
练习 1:Riemann 和
- 用 Python 写一个函数:
python
def left_riemann(f, a, b, N):- 用左端点法近似计算:
∫01(3x2+1)dx\int_0^1(3x^2+1)dx∫01(3x2+1)dx - 并观察 N = 10, 100, 1000 时的结果。
- 左端点法(Left Riemann Sum)是 最基础、最直观的定积分近似方法,它直接来自我们在曲线下画一排"小矩形"累加面积的想法。
- 在每个小区间中,用左端点的函数值当作矩形高度来估计面积。
- 例子:想近似计算:
∫02x2dx\int_0^2x^2dx∫02x2dx - 将区间 [0,2] 分成 4 份(为了看清楚):
text
第 1 段:x ∈ [0,0.5],左端点是 x=0
第 2 段:x ∈ [0.5,1],左端点是 x=0.5
第 3 段:x ∈ [1,1.5],左端点是 x=1
第 4 段:x ∈ [1.5,2],左端点是 x=1.5- 每一段画一个"高度 = 左端点的函数值"的矩形。
解题 1
python
import numpy as np
def left_riemann(f, a, b, N):
area_sum = 0
xl = (b-a) / N # dx 小矩形宽度
for n in range(N):
xs = a + n*xl # 每个小矩形左端点的坐标
hs = f(xs) # 带入左端点 x 的坐标求出对应的函数值,也就是每个小矩形的高
area = xl * hs # 计算小矩形的面积
area_sum += area # 把所有小矩形的面积加起来
return area_sum
# test
f = lambda x: 3*x**2 + 1
for N in [10, 100, 1000, 10000]:
print(left_riemann(f, 0, 1, N))1.8550000000000002
1.9850499999999998
1.9985004999999965
1.9998500049999988练习 2:图像理解
- 画出 f(x)=x³ − x 在区间 [-2, 2] 上的图像,并用填充颜色的方式展示"曲线下的面积"。
- 提示:
python
plt.fill_between(xs, f(xs), alpha=0.3)
python
import numpy as np
import matplotlib.pyplot as plt
xs = np.linspace(-2, 2, 400)
ys = xs**3 - xs
plt.axhline(0, color='black', linewidth=0.7)
plt.plot(xs, ys, label='f(x)')
plt.fill_between(xs, ys, alpha=0.3)
plt.legend()
plt.show()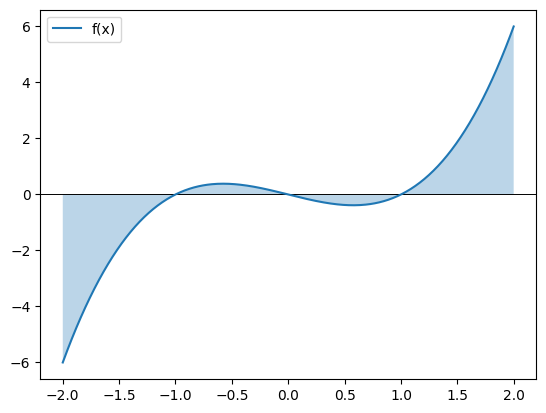
练习 3:简单定积分求值
- 无需用反导数,只用数学公式求:
∫03(2x+1)dx\int_0^3(2x+1)dx∫03(2x+1)dx
解题 3
f′(x)=2x+1,f(x)=x2+x+Cf'(x)=2x+1, f(x)=x^2+x+Cf′(x)=2x+1,f(x)=x2+x+C
∫03(2x+1)dx=f(3)−f(0)=12+C−C=12\int_0^3(2x+1)dx=f(3)-f(0)=12+C-C=12∫03(2x+1)dx=f(3)−f(0)=12+C−C=12
练习 4(较难,但非常重要)
- 判断以下两个函数哪部分面积是负的:
- f(x)=x−1在[0,3]f(x)=x-1\text{在}[0,3]f(x)=x−1在[0,3]
- f(x)=x2−4在[−3,3]f(x)=x^2-4\text{在}[-3,3]f(x)=x2−4在[−3,3]
- 并解释理由。
解题 4
-
对于f(x)=x−1在[0,3]f(x)=x-1\text{在}[0,3]f(x)=x−1在[0,3]:
思路:面积其实就是dx×hsdx\times hsdx×hs,dxdxdx是正值,那么要想面积为负,只能是hshshs是负值,而h=f(x)h = f(x)h=f(x),只要找到函数值为负数的区间就可以了
令f(x)=x−1<0f(x)=x-1<0f(x)=x−1<0,则x<1x<1x<1,则在[0,3][0,3][0,3]上面积为负的区间为[0,1)[0,1)[0,1)
-
对于f(x)=x2−4在[−3,3]f(x)=x^2-4\text{在}[-3,3]f(x)=x2−4在[−3,3]:
同样令f(x)=x2−4<0f(x)=x^2-4<0f(x)=x2−4<0,则x2<4x^2<4x2<4,解得−2<x<2-2<x<2−2<x<2,则在[−3,3][-3,3][−3,3]上面积为负的区间为(−2,2)(-2,2)(−2,2)