算法竞赛之排序算法

[一.插入排序（Insertion Sort）](#一.插入排序（Insertion Sort）)
- 1.概念
- 2.实现逻辑
- - [2.1 关键理解](#2.1 关键理解)
  - [2.2 插入排序实现逻辑（简述）](#2.2 插入排序实现逻辑（简述）)
  - [2.3 特点补充](#2.3 特点补充)
  - [2.4 示例（以整数数组为例）](#2.4 示例（以整数数组为例）)
- 3.参考代码
[二.选择排序（Selection Sort）](#二.选择排序（Selection Sort）)
- 1.概念以及实现思路
- - [1.1 选择排序的概念](#1.1 选择排序的概念)
  - - 核心特征：
  - [1.2 选择排序的实现思路](#1.2 选择排序的实现思路)
  - - 整体流程：
    - [步骤拆解（以数组 `[5, 2, 4, 6, 1]` 为例）：](#步骤拆解（以数组 [5, 2, 4, 6, 1] 为例）：)
    - 算法特性补充
- 2.参考代码
[三.冒泡排序(Bubble Sort)](#三.冒泡排序(Bubble Sort))
- [1. 概念及实现逻辑](#1. 概念及实现逻辑)
- - [1.1 核心逻辑：](#1.1 核心逻辑：)
  - [1.2 示例](#1.2 示例)
- 2.参考代码
[四.堆排序（Heap Sort）](#四.堆排序（Heap Sort）)
- 1.概念
- 2.实现思路
- - 2.1代码核心前提
  - 2.2实现思路
  - - [1 辅助函数`down`：调整大根堆](#1 辅助函数down：调整大根堆)
    - [2 主函数`HeapSort`](#2 主函数HeapSort)
  - [2.3 核心总结](#2.3 核心总结)
  - [2.4 特性](#2.4 特性)
- 3.参考代码
[五.快速排序（Quick Sort）](#五.快速排序（Quick Sort）)
- [1. 快速排序的概念](#1. 快速排序的概念)
- [2. 实现思路](#2. 实现思路)
- - [2.1 基准值选取：随机化优化](#2.1 基准值选取：随机化优化)
  - [2.2 三向划分操作（核心步骤）](#2.2 三向划分操作（核心步骤）)
  - [2.3 递归分治](#2.3 递归分治)
  - [2.4 整体流程总结](#2.4 整体流程总结)
- 3.参考代码
[六.归并排序（Merge Sort）](#六.归并排序（Merge Sort）)
- 1.概念
- 2.实现思路
- - [2.1 递归划分（分阶段）](#2.1 递归划分（分阶段）)
  - [2.2 合并有序区间（合阶段）](#2.2 合并有序区间（合阶段）)
  - [2.3 整体流程总结](#2.3 整体流程总结)
- 3.参考代码
七.六大排序测试
- [1. 算法时间复杂度差异显著](#1. 算法时间复杂度差异显著)
- [2. O(n log n)类算法（堆/快排/归并）性能优势极大](#2. O(n log n)类算法（堆/快排/归并）性能优势极大)
- [3. 同复杂度算法的实际表现差异](#3. 同复杂度算法的实际表现差异)
- [4. 实际场景的算法选择建议](#4. 实际场景的算法选择建议)

Hello，小伙伴们！又到了咱们一起捣鼓代码的时间啦！💪 把生活调成热情模式，带着满满的能量钻进编程的奇妙世界吧------今天也要写出超酷的代码，冲鸭！🚀

我的博客主页：喜欢吃燃面
我的专栏：《C语言》，《C语言之数据结构》，《C++》，《Linux学习笔记》
感谢你点开这篇博客呀！真心希望这些内容能给你带来实实在在的帮助～如果你有任何想法或疑问，非常欢迎一起交流探讨，咱们互相学习、共同进步，在编程路上结伴成长呀！</font
注：为了方便演示，本文所有排序算法，考虑的都是升序情况。

一.插入排序（Insertion Sort）

1.概念

插入排序(Insertion Sort)类似于玩扑克牌插牌过程，每次将一个待排序的元素按照其关键字 （用于比较大小的核心数据，如数字大小、字符串字典序等）大小，插入到前面已排好序的序列 中，按照该种方式将所有元素全部插入完成即可。

2.实现逻辑

2.1 关键理解

核心关键 ：待排序元素的比较依据（如数字的数值大小、字符串的字典序、自定义对象的特定属性值等），是插入排序中判断元素位置的核心标准。
操作关键 ：
- 已排序序列：初始为第一个元素，后续逐步扩展。
- 待插入元素：从第二个元素开始，逐个选取的未排序元素。
- 向前比较与后移：将待插入元素与已排序序列从后往前比较，大于待插入元素的已排序元素向后移位，腾出插入位置。
- 插入位置：找到第一个小于/等于待插入元素的位置，将待插入元素放入。

2.2 插入排序实现逻辑（简述）

插入排序采用逐步构建有序序列的思路，核心步骤如下：

初始化：将数组的第一个元素视为长度为1的"已排序序列"，从第二个元素（索引1）开始，依次作为"待插入元素"。
遍历待插入元素 ：对每个待插入元素，执行以下操作：
- 暂存待插入元素的值（避免移位时被覆盖）。
- 从已排序序列的末尾（当前待插入元素的前一个位置）开始，向前遍历已排序序列：
  - 若已排序元素的关键字大于待插入元素的关键字，将该已排序元素向后移位（覆盖下一个位置）。
  - 若遇到已排序元素的关键字小于/等于待插入元素，或遍历到已排序序列的起始位置，停止比较。
- 将暂存的待插入元素插入到最终腾出的位置。
终止条件：所有待插入元素处理完毕，整个数组成为有序序列。

2.3 特点补充

时间复杂度：最好情况（已排序） O ( n ) O(n) O(n)，最坏情况（逆序） O ( n 2 ) O(n^2) O(n2)，平均 O ( n 2 ) O(n^2) O(n2)。
空间复杂度： O ( 1 ) O(1) O(1)（原地排序，仅需临时变量存储待插入元素）。
稳定性：稳定排序（相等关键字的元素相对位置不变）。

2.4 示例（以整数数组为例）

数组 [5, 2, 4, 6, 1] 的插入排序过程：

已排序：[5]，待插入：2 → 5>2，5后移，插入2 → [2,5]。
待插入：4 → 5>4，5后移，2<4，插入4 → [2,4,5]。
待插入：6 → 5<6，直接插入末尾 → [2,4,5,6]。
待插入：1 → 6、5、4、2均>1，依次后移，插入起始位置 → [1,2,4,5,6]。

3.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 直接插入排序
void InsertSort()
{
	// 从第2个元素开始，逐个插入前面有序区间
	for (int i = 2; i <= n; i++)
	{
		int key = a[i]; // 当前待插入元素
		int j = i - 1;  // 有序区间末尾指针

		// 找到key的插入位置（比key大的元素后移）
		while (j >= 1 && a[j] > key)
		{
			a[j + 1] = a[j];
			j--;
		}
		a[j + 1] = key; // 插入key到正确位置
	}
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	InsertSort();  // 执行插入排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

二.选择排序（Selection Sort）

1.概念以及实现思路

1.1 选择排序的概念

选择排序（Selection Sort）是一种不稳定的原地排序算法 ，核心思想是将待排序序列划分为「已排序部分」和「未排序部分」，每次从未排序部分中找到关键字（如数值大小、字典序等）最小（或最大）的元素，将其与未排序部分的第一个元素交换位置，从而将该最小元素纳入「已排序部分」的末尾。重复此过程，直到所有元素均被纳入已排序部分，完成排序。

核心特征：

划分逻辑：已排序部分初始为空，未排序部分为整个序列；每轮迭代后，已排序部分长度+1，未排序部分长度-1。
操作核心："选择"（找未排序部分的极值）+ "交换"（将极值放到已排序部分末尾）。
稳定性：不稳定（例如序列 [2, 2, 1]，第一轮选择最小元素 1 与第一个 2 交换，两个 2 的相对位置会改变）。

1.2 选择排序的实现思路

整体流程：

初始化划分 ：将数组 arr 分为已排序区（初始为空）和未排序区（初始为 arr[0...n-1]），用变量 i 表示未排序区的起始索引（即已排序区的末尾索引+1），i 从 0 遍历到 n-2（因为最后一个元素无需再选择）。
查找极值 ：对于每一轮的未排序区 arr[i...n-1]，遍历该区间，找到关键字最小的元素，记录其索引 min_idx。
交换元素 ：将未排序区的第一个元素 arr[i] 与最小元素 arr[min_idx] 交换，此时 arr[i] 成为已排序区的最后一个元素，未排序区起始索引 i 后移一位。
终止条件 ：当 i 遍历到 n-1 时，未排序区仅剩一个元素，自然属于已排序区，排序完成。

步骤拆解（以数组 `[5, 2, 4, 6, 1]` 为例）：

轮次	已排序区	未排序区	未排序区最小元素	交换操作	结果序列
初始	`[]`	`[5,2,4,6,1]`	-	-	`[5,2,4,6,1]`
1	`[]`	`[5,2,4,6,1]`	`1`（索引4）	交换索引0和4	`[1,2,4,6,5]`
2	`[1]`	`[2,4,6,5]`	`2`（索引1）	无需交换	`[1,2,4,6,5]`
3	`[1,2]`	`[4,6,5]`	`4`（索引2）	无需交换	`[1,2,4,6,5]`
4	`[1,2,4]`	`[6,5]`	`5`（索引4）	交换索引3和4	`[1,2,4,5,6]`
结束	`[1,2,4,5,6]`	`[]`	-	-	排序完成

算法特性补充

时间复杂度 ：
- 最好、最坏、平均情况均为 O ( n 2 ) O(n^2) O(n2)（无论序列是否有序，都需要遍历未排序区找极值，外层循环 n − 1 n-1 n−1 次，内层循环平均 n / 2 n/2 n/2 次）。
空间复杂度 ： O ( 1 ) O(1) O(1)（原地排序，仅需临时变量存储索引和交换元素）。
适用场景 ：
- 适合小规模数据排序，或对空间复杂度要求极高的场景。
- 不适合需要稳定排序的场景（如需稳定，可调整交换逻辑为"移动"而非直接交换，但会增加时间开销）。

2.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 选择排序
void SelectSort()
{
	for (int i = 1; i <= n; i++)  // 每次确定第i位最小值
	{
		int pos = i;               // 记录最小值下标
		for (int j = i; j <= n; j++)
		{
			if (a[pos] > a[j]) pos = j;  // 更新最小值下标
		}
		swap(a[pos], a[i]);  // 最小值交换到第i位
	}
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	SelsctSort();  // 执行选择排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

三.冒泡排序(Bubble Sort)

1. 概念及实现逻辑

冒泡排序(Bubble Sort)也是⼀种简单的排序算法。它的⼯作原理是每次检查相邻两个元素，如果前⾯的元素与后⾯的元素满⾜给定的排序条件，就将相邻两个元素交换。当没有相邻的元素需要交换时，排序就完成了。

1.1 核心逻辑：

排序方向：通常升序排序时，若前一个元素大于后一个元素，则交换，每一轮遍历会将未排序部分的最大元素"冒泡"到末尾，成为已排序部分的起始。
优化点：可设置标志位，若某一轮遍历中没有发生交换，说明序列已完全有序，可直接终止排序，减少不必要的遍历。
算法特性 ：
- 时间复杂度：最好情况（已排序） O ( n ) O(n) O(n)，最坏情况（逆序） O ( n 2 ) O(n^2) O(n2)，平均 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度： O ( 1 ) O(1) O(1)（原地排序）。
- 稳定性：稳定排序（相等元素的相对位置不变）。

1.2 示例

（数组 [5, 2, 4, 6, 1]）：

第一轮：比较交换后 [2, 4, 5, 1, 6]（最大元素6冒泡到末尾）
第二轮：比较交换后 [2, 4, 1, 5, 6]（次大元素5冒泡到倒数第二位）
第三轮：比较交换后 [2, 1, 4, 5, 6]（元素4到位）
第四轮：比较交换后 [1, 2, 4, 5, 6]（元素2到位）
第五轮：无交换，排序完成

2.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 冒泡排序
void BubbleSort()
{
	for (int i = n; i > 1; i--)  // 每次冒泡确定末尾1个最大值
	{
		int flag = 0;             // 标记是否发生交换（无交换则有序）
		for (int j = 1; j < i; j++)
		{
			if (a[j] > a[j + 1])
			{
				swap(a[j], a[j + 1]);
				flag = 1;
			}
		}
		if (!flag) break;  // 无交换，直接退出
	}
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	BubbleSort();  // 执行冒泡排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

四.堆排序（Heap Sort）

1.概念

堆排序是基于堆（完全二叉树，满足堆序性） 的不稳定原地排序算法，核心逻辑：

将待排序数组构建为大顶堆（升序）/小顶堆（降序），堆顶为极值；
交换堆顶与未排序部分末尾元素，固定极值到有序区；
调整剩余元素为新堆，重复上述步骤直至排序完成。

堆排序的本质 ：

堆排序的本质是：借助堆这种数据结构的"极值置顶"特性，将无序序列转化为有序序列的选择排序优化版。

2.实现思路

2.1代码核心前提

采用1-based数组索引（堆顶为索引1），完全二叉树特性：

父节点parent的左孩子2*parent、右孩子2*parent+1；
最后一个非叶子节点索引为n/2；
a为全局待排序数组，n为有效元素个数。

2.2实现思路

1 辅助函数`down`：调整大根堆

计算父节点左孩子child = 2*parent；
循环判断孩子是否在堆范围内：
- 选左右孩子中较大者；
- 父节点≥孩子则退出，否则交换父子节点，继续向下调整。

2 主函数`HeapSort`

构建大根堆：从n/2倒序到1，调用down调整每个节点；
提取极值并调整：
- 交换堆顶（最大值）与堆尾，固定到有序区；
- 缩小堆范围，调用down重新调整堆顶；
- 重复至堆仅剩1个元素。

2.3 核心总结

先构建大根堆，再反复交换堆顶与堆尾、调整堆结构，最终得到升序数组。

2.4 特性

时间复杂度： O ( n log ⁡ n ) O(n\log n) O(nlogn)；
空间复杂度： O ( 1 ) O(1) O(1)（原地排序）；
稳定性：不稳定。

3.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 堆排序辅助：向下调整大根堆（parent为当前节点，size为堆有效大小）
void down(int parent, int size)
{
	int child = 2 * parent;  // 左孩子下标（完全二叉树特性）
	while (child <= size)    // 孩子节点在堆范围内
	{
		// 选择左右孩子中较大的一个
		if (child + 1 <= size && a[child] < a[child + 1]) child++;
		if (a[parent] >= a[child]) return;  // 满足大根堆，直接返回

		swap(a[parent], a[child]);  // 交换父子节点
		parent = child;             // 继续向下调整
		child = parent * 2;
	}
}

// 堆排序
void HeapSort()
{
	// 1. 构建大根堆（从最后一个非叶子节点n/2开始调整）
	for (int i = n / 2; i >= 1; i--) down(i, n);
	// 2. 堆顶（最大值）与堆尾交换，缩小堆范围并调整
	for (int i = n; i > 1; i--)
	{
		swap(a[1], a[i]);  // 最大值移到数组末尾
		down(1, i - 1);    // 调整剩余堆为大根堆
	}
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	HeapSort();  // 执行堆排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

五.快速排序（Quick Sort）

1. 快速排序的概念

快速排序是基于分治思想 的不稳定原地排序算法，核心逻辑是选取一个基准值，将待排序序列划分为"小于基准""等于基准""大于基准"三个部分，随后递归处理"小于基准"和"大于基准"的子序列，直至所有子序列长度为1（天然有序），最终实现整体排序。该算法平均时间复杂度为 O ( n log ⁡ n ) O(n\log n) O(nlogn)，通过随机选取基准值可避免最坏情况下的 O ( n 2 ) O(n^2) O(n2) 时间复杂度，是实际工程中应用广泛的高效排序算法。

2. 实现思路

2.1 基准值选取：随机化优化

代码通过 GetRandom 函数从当前排序区间 [left, right] 中随机选取一个元素作为基准值 p，而非固定选首/尾元素，目的是避免有序序列导致的划分失衡，优化时间复杂度。

2.2 三向划分操作（核心步骤）

初始化指针：l 标记"小于基准"区域的末尾（初始为 left-1），i 为遍历指针（初始为 left），r 标记"大于基准"区域的起始（初始为 right+1）。
遍历划分：当 i < r 时，根据当前元素 a[i] 与基准 p 的大小关系处理：
- 若 a[i] < p：将 a[i] 划入"小于基准"区域，l 右移，交换 a[l] 与 a[i]，i 右移；
- 若 a[i] > p：将 a[i] 划入"大于基准"区域，r 左移，交换 a[r] 与 a[i]（i 不移动，需重新检查交换后的新元素）；
- 若 a[i] == p：直接 i 右移，划入"等于基准"区域。
划分结果：最终序列被分为 [left, l]（小于 p）、[l+1, r-1]（等于 p）、[r, right]（大于 p）三部分，"等于基准"的元素已处于正确位置，无需再处理。

2.3 递归分治

递归调用 QuickSort(left, l) 处理"小于基准"的子序列，调用 QuickSort(r, right) 处理"大于基准"的子序列；当 left >= right 时，子序列长度≤1，递归终止。

2.4 整体流程总结

通过随机选基准值减少划分失衡风险，再通过三向划分将序列拆分为"小于、等于、大于"基准的三部分，递归处理前后子序列，最终实现整体有序。这种三向划分方式对存在大量重复元素的序列优化效果显著，可减少递归次数和交换操作。

3.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 从[left, right]随机选一个元素作为基准值
int GetRandom(int left, int right)
{
    // 生成区间内随机索引并返回对应元素
    int randomIdx = rand() % (right - left + 1) + left;
    return a[randomIdx];
}

// 快速排序（三向划分版），排序区间[left, right]
void QuickSort(int left, int right)
{
    // 递归终止：区间长度≤1
    if (left >= right) return;

    // 随机选基准值，避免划分失衡
    int p = GetRandom(left, right);

    // l：小于基准区末尾；i：遍历指针；r：大于基准区起始
    int l = left - 1, i = left, r = right + 1;

    // 三向划分：[小于p, 等于p, 大于p]
    while (i < r)
    {
        if (a[i] < p)      // 划入小于区
            swap(a[++l], a[i++]);
        else if (a[i] > p) // 划入大于区
            swap(a[--r], a[i]);
        else               // 等于基准，直接后移
            i++;
    }

    // 递归排序小于区和大于区，等于区无需处理
    QuickSort(left, l);
    QuickSort(r, right);
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	QuickSort();  // 执行快速排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

六.归并排序（Merge Sort）

1.概念

归并排序是一种时间复杂度稳定为 O(n log n) 的排序算法，无论待排序数据的分布特性如何（如有序、逆序、含重复元素等），其时间复杂度均保持这一水平，这是它区别于快速排序等算法的核心优势之一。

归并排序的核心思想是分治策略（在这里简述一下），整体执行过程主要分为两个核心步骤：

分：将当前待排序区间从中间位置一分为二，递归调用归并排序，分别对左、右两个子区间进行排序，直到子区间长度为 1（天然有序）；
合：将两个已排序的子区间合并为一个有序区间，这一步的逻辑与顺序表中"合并两个有序序列"的算法题思路一致。

简言之，归并排序通过递归实现"分"的过程，再通过合并操作完成"治"的过程，最终实现整体序列的有序。

2.实现思路

2.1 递归划分（分阶段）

终止条件 ：当排序区间 [left, right] 满足 left >= right 时，子区间长度≤1，天然有序，直接返回。
划分操作 ：计算区间中点 mid = (left + right) >> 1（等价于 (left+right)/2），递归调用 MergeSort(left, mid) 排序左半区间，递归调用 MergeSort(mid+1, right) 排序右半区间，直到所有子区间都被划分为长度为1的单元。

2.2 合并有序区间（合阶段）

指针初始化 ：定义 cur1（左半区间起始指针）、cur2（右半区间起始指针）、i（临时数组 tmp 的写入指针），均从对应区间起始位置开始。
双指针合并 ：循环比较 a[cur1] 和 a[cur2]，将较小的元素存入临时数组 tmp，并移动对应指针；当其中一个区间遍历完毕，将另一个区间的剩余元素直接追加到 tmp 末尾。
写回原数组 ：将临时数组 tmp 中有序的元素覆盖写回原数组 a 的对应区间，完成当前层级的合并。

2.3 整体流程总结

通过递归将原数组不断划分为更小的子区间，直到子区间有序；再从最小的有序子区间开始，逐层合并为更大的有序区间，最终整个数组完成排序。临时数组 tmp 用于合并过程中暂存数据，避免直接修改原数组导致数据覆盖。

3.参考代码

cpp 复制代码

#include<iostream>
using namespace std;

const int N = 1e4 + 10; // 数组最大容量（满足题目需求）
int a[N]; // 存储待排序数组
int n;    // 数组实际长度

// 打印数组元素
void Print()
{
	for (int i = 1; i <= n; i++) cout << a[i] << " ";
	cout << endl;
}

// 全局临时数组，用于合并阶段暂存数据
int tmp[N];
// 归并排序主函数，排序区间 [left, right]
void MergeSort(int left, int right)
{
    // 递归终止：区间长度 <= 1，天然有序
    if (left >= right) return;

    // 划分中点，右移等价于除以2
    int mid = (left + right) >> 1;
    // 递归排序左半区间
    MergeSort(left, mid);
    // 递归排序右半区间
    MergeSort(mid + 1, right);

    // 合并两个有序区间：cur1左区指针，cur2右区指针，i临时数组指针
    int cur1 = left, cur2 = mid + 1, i = left;
    // 双指针遍历，按序存入临时数组
    while (cur1 <= mid && cur2 <= right)
    {
        if (a[cur1] <= a[cur2]) tmp[i++] = a[cur1++];
        else tmp[i++] = a[cur2++];
    }
    // 处理左区剩余元素
    while (cur1 <= mid) tmp[i++] = a[cur1++];
    // 处理右区剩余元素
    while (cur2 <= right) tmp[i++] = a[cur2++];

    // 临时数组有序数据写回原数组
    for (int j = left; j <= right; j++) a[j] = tmp[j];
}

// 测试函数：输入数据→打印原数组→排序→打印有序数组
void test()
{
	// 测试数据：37 12 89 5 73 41 92 26 68 19
	n = 10;
	for (int i = 1; i <= n; i++) cin >> a[i]; // 输入10个测试数
	Print();       // 打印原始数组
	MergeSort();  // 执行归并排序
	Print();       // 打印排序后数组
}

int main()
{
	test(); // 启动测试
	return 0;
}

//测试结果：
37 12 89 5 73 41 92 26 68 19
37 12 89 5 73 41 92 26 68 19
5 12 19 26 37 41 68 73 89 92

七.六大排序测试

cpp 复制代码

// 测试归并排序耗时 
void TestMergeSort(int size)
{
	n = size;
	a.resize(n + 10);
	srand((unsigned int)time(0));
	for (int i = 1; i <= n; i++) {
		a[i] = rand() % 1000000;
	}

	// 计时并执行排序
	clock_t st = clock();
	MergeSort(1, n);  // 修正：调用MergeSort而非QuickSort
	clock_t ed = clock();

	// 计算并输出耗时（毫秒）
	double ms = (double)(ed - st) * 1000 / CLOCKS_PER_SEC;
	cout << "MergeSort:" << ms << " ms" << endl;
}

// 通用排序耗时测量函数：sortFunc为排序函数，size为数据量，name为算法名
void measureSort(void (*sortFunc)(), int size, const string& name) {
	// 初始化随机数组
	n = size;
	a.resize(n + 10);
	srand((unsigned int)time(0));
	for (int i = 1; i <= n; i++) {
		a[i] = rand() % 1000000;
	}

	// 计时并执行排序
	clock_t st = clock();
	sortFunc();
	clock_t ed = clock();

	// 输出耗时
	double ms = (double)(ed - st) * 1000 / CLOCKS_PER_SEC;
	cout << name << ": " << ms << " ms" << endl;
}

int main()
{
	// 测试2万条数据的6种排序算法耗时
	measureSort(InsertSort, 2 * 1e4, "InsertSort");
	measureSort(SelectSort, 2 * 1e4, "SelectSort");
	measureSort(BubbleSort, 2 * 1e4, "BubbleSort");
	measureSort(HeapSort, 2 * 1e4, "HeapSort");
	TestQuickSort(2 * 1e4);
	TestMergeSort(2 * 1e4);  

	return 0;
}

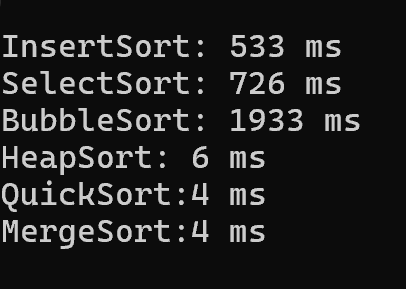
从20000个随机数字的排序耗时结果，可以得出以下结论：

1. 算法时间复杂度差异显著

O(n²)类算法（插入/选择/冒泡） ：耗时远高于O(n log n)类算法
- 冒泡排序耗时最久（1933 ms），选择排序次之（726 ms），插入排序相对稍快（533 ms）；
- 这类算法在数据量达到2万时，时间开销会随数据量增长呈平方级膨胀，仅适合小规模数据。

2. O(n log n)类算法（堆/快排/归并）性能优势极大

堆排序（6 ms）、快速排序（4 ms）、归并排序（4 ms）耗时都在个位数级别，效率是O(n²)算法的数百倍；
快排和归并排序耗时几乎一致，是大数量级数据排序的首选。

3. 同复杂度算法的实际表现差异

快速排序和归并排序（均为O(n log n)）实际耗时相同，说明在随机数据下，两者的常数项开销接近；
堆排序耗时略高于快排/归并，因为堆的调整操作（如down函数）存在更多的数组访问开销。

4. 实际场景的算法选择建议

若数据量小（如≤100）：可选用插入排序（实现简单、常数项小）；
若数据量大（如≥1000）：优先选择快排/归并排序（平衡了效率和稳定性）；
若对内存开销敏感：堆排序（原地排序，空间复杂度O(1)）更合适。

算法竞赛之排序算法

目录

一.插入排序（Insertion Sort）

1.概念

2.实现逻辑

2.1 关键理解

2.2 插入排序实现逻辑（简述）

2.3 特点补充

2.4 示例（以整数数组为例）

3.参考代码

二.选择排序（Selection Sort）

1.概念以及实现思路

1.1 选择排序的概念

核心特征：

1.2 选择排序的实现思路

整体流程：

步骤拆解（以数组 [5, 2, 4, 6, 1] 为例）：

算法特性补充

2.参考代码

三.冒泡排序(Bubble Sort)

1. 概念及实现逻辑

1.1 核心逻辑：

1.2 示例

2.参考代码

四.堆排序（Heap Sort）

1.概念

2.实现思路

2.1代码核心前提

2.2实现思路

1 辅助函数down：调整大根堆

2 主函数HeapSort

2.3 核心总结

2.4 特性

3.参考代码

五.快速排序（Quick Sort）

1. 快速排序的概念

2. 实现思路

2.1 基准值选取：随机化优化

2.2 三向划分操作（核心步骤）

2.3 递归分治

2.4 整体流程总结

3.参考代码

六.归并排序（Merge Sort）

1.概念

2.实现思路

2.1 递归划分（分阶段）

2.2 合并有序区间（合阶段）

2.3 整体流程总结

3.参考代码

七.六大排序测试

1. 算法时间复杂度差异显著

2. O(n log n)类算法（堆/快排/归并）性能优势极大

3. 同复杂度算法的实际表现差异

4. 实际场景的算法选择建议

步骤拆解（以数组 `[5, 2, 4, 6, 1]` 为例）：

1 辅助函数`down`：调整大根堆

2 主函数`HeapSort`