二分查找算法

算法介绍

二分查找算法的特点：最恶心，细节最多，最容易写出死循环的算法。

使用：只要发现数组中的规律，能够使用二分查找，就能使用二分查找算法。数组不一定需要有序，只要存在二分性，就可以使用二分查找算法。

此外二分查找算法是存在模板的，接下来会根据题目，依次介绍三个模板：1. 朴素二分模板（适用范围局限），2. 查找左边界的二分模板，3. 查找右边界的二分模板（2.3模板是万能的，但是细节繁多）。模板不需要死记，根据你分析出来二段性去使用即可。

什么是二段性？当数组有规律，依照这个规律，选取数组中的某个位置，能将数组分成两个部分，之后再根据规律能够有选择性的舍去一部分，再在另一部分中去查找。

---

算法题目

题目1：704. 二分查找 - 力扣（LeetCode）

题目解析

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。

---

题目示例

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

---

算法原理

来看一个序列：-1,0,3,5,9,12 ，target = 9。

利用序列升序的特点，以中间值5为分割，左边的数都是小于5的，右边的数都是大于等于5的，如果target大于5，那么target肯定不在5的左边，因此可以排除左区间，只看右区间。再从右区间中找到中间值，分为左右区间，继续逐一排查。当数组具有二段性的时候，就可以使用二分查找算法。

选取的位置可以是二分之一处，三分之一处，四分之一处等等，为什么可以取这么多的位置，选取的位置需要按照题目来具体分析。由概率学计算得出，当选取的位置为二分之一处时，时间复杂度最小。

选取中间位置为划分点，刚开始时，用 mid 指向区间的中点，left 指向区间的最左边，right 指向区间的最右边，mid 位置的值用 val 表示。让 val 与 target 作比较，若 val 值小于 target，则去掉左区间，更新 left 的值，left = mid + 1，再在新的 left 和 right 组成的区间中寻找 target；若 val 值大于 target，则去掉右区间，更新 right 的值，right = mid -- 1，再在新的 left 和 right 组成的区间中寻找 target；若 val 等于 target，则直接返回结果。当 left == right 时，此时所指向的位置的元素仍然是未知的，也要让它与 target 比较。所以比较的循环条件为left <= right。这就是朴素二分查找算的核心逻辑。

为什么最终找到的结果是正确的？与暴力解法遍历一样，只是二分查找算法依据了数组的特性，将部分数据排除了，暴力循环找到的结果是正确的，则二分查找的结果也是正确的。

---

代码实现

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        
        while(left <= right)
        {
            // 这么初始化 mid 是为了避免溢出风险
            // int mid = (right + left) / 2;
            int mid = left + (right - left) / 2;

            // 当 mid > target,right = mid - 1
            if(nums[mid] > target) { right = mid - 1; }
            // 当 mid < target,left = mid + 1
            else if(nums[mid] < target) { left = mid + 1; }
            // 当 mid == targte,返回mid
            else { return mid; }
        }

        // 找不到，返回-1
        return -1;
    }
};

---

总结朴素二分查找的模板

while(left <= right)
{
    int mid = left + (right - left) / 2; // 防溢出        
    if(......) { right = mid - 1; }
    else if(......) { left = mid + 1; }
    else { return ......; }
}

...... 根据具体题目所分析出的二段性去填写。mid 也可以写成这样： int mid = left + (right -- left + 1) / 2。

---

题目2：34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目分析

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

---

题目示例

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

---

算法原理

示例：序列 1，2，3，3，3，4，5；target = 3。

定义两个指针，left和right，计算它们的中点 mid ，mid指向的值用 val 表示。left 指向值为1的位置，right 指向值为5的位置，mid 指向下标为3的位置，val = 3。val == target，但是我们不能判断此时 mid 指向的值就是数组的边界。所以还需要 mid 向前向后找边界，如果序列为 3，3，3，3，3，3，3；target = 3时，使用朴素二分查找的时间复杂度为O(N)。朴素二分查找没有利用数组有序的特性。

尝试优化二分查找算法。二分查找的本质就是寻找数组的二段性，那这道题存在二段性吗？

将查找区间的左端点和右端点分开进行。

查找区间的左端点

序列 1,2,3,3,3,4,5 ，target = 3，该序列的区间的左端点为下标2，再来看以下标2为界限，它的左右边的元素有什么特点？它的左边的值都小于等于 target，右边的值都大于 target。这就是该题的二段性。

若 val < target，则就相当于 mid 落在 [1,2] 区间，显然是找不到最终结果的，此时让 left = mid + 1，接着在新的 [left,right] 区间中定位 mid，寻找左端点。

若 val >= target，大于和等于要在一起讨论，为什么？因为val == target 时，可能 mid 不是左端点。当 val >= target 时，mid 就相当于落在了[3,3,3,4,5]区间中。此时如何更新 right 呢？若让 right = mid -- 1，这样会出现问题，若 mid 此时的指向就是左端点呢？让 right = mid -- 1，在 mid 的前面区域去找左端点，那是找不到的。所以应该让 right = mid，接着在新的 [left,right] 区间中定位 mid，寻找左端点。

总结：若 val < target，left = mid + 1；若 val >= target，right = mid。

细节处理

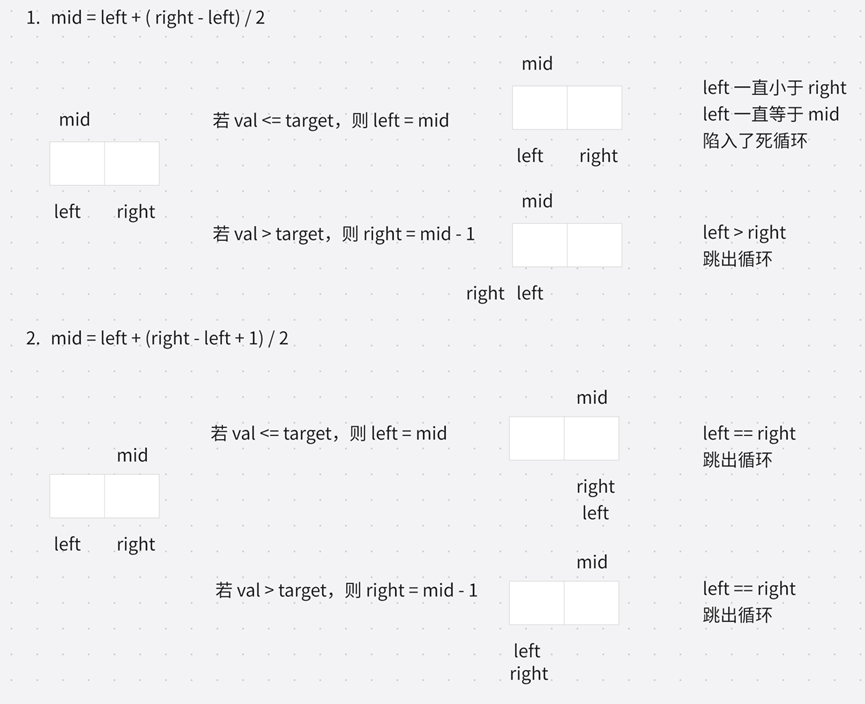
循环条件：和朴素二分查找一样，循环条件无非两个 left <= right，left < right，选择哪一个呢？

若选择 left < right 作为循环条件

1. left，right\]区间中存在结果

2. left，right\]区间的值全部大于 target

3. left，right\]区间的值全部小于target

---

若循环条件为 left <= right

当处于 [left,right] 区间存在结果这种情况时，会出现死循环，最终 left == right，val >= target，right = mid，right一直不移动，循环继续进行，如此一来就形成了死循环。所以当 left == right 时，就无需判断了。

---

因此循环条件为：left < right。

中点 mid 的求取

求中点由两种方法： mid = left + (right -- left) / 2， mid = left + (right -- left + 1) / 2。

所以应该选择第一种求mid的方法，即 mid = left + (right -- left) / 2。

查找区间右端点

序列 1，2，3，3，3，4，5；target = 3。该序列的区间的右端点为下标4的位置，再来看以下标4为界限，它的左右边的元素有什么特点？它的左边的值都小于等于 target，右边的值都大于target。这就是该题的二段性。

若 val <= target，相当于 mid 落在 [1,2,3,3,3] 区间，最终点就位于该区间内，如何更新 left，让 left = mid ，继续在新的 left 和 right 区间寻找右端点；若 val > target，相当于 mid 落在 [4,5] 区间，最终点在该区间是找不到的，更新 right 的指向，right = mid -- 1，继续在新的 left 和 right 区间寻找右端点。

总结：若 val <= target，left = mid；若 val > target，right = mid -- 1。

细节处理

循环条件，原理与左端点一致，left < right。

中点的求取，两种方法：mid = left + (right -- left) / 2，mid = left + (right -- left + 1 ) / 2。

所以选择第二种求 mid 的方法，即 mid = left + (right -- left + 1) / 2。

---

代码实现

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        vector<int> ret = { -1, -1 }; // 定义返回值
        
        // 查找左端点
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            // 若 mid < target,left = mid + 1
            if(nums[mid] < target){ left = mid + 1; }
            // 若 mid >= target,right = mid
            else{ right = mid; }
        }
        // 找到左端点
        if(left == right && nums[left] == target){ ret[0] = left; }

        // 重置
        left = 0;
        right = nums.size() - 1;

        // 查找右端点
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            // 若 mid > target,right = mid - 1
            if(nums[mid] > target){ right = mid - 1; }
            // 若 mid <= target,left = mid
            else{ left = mid; }
        }
        // 找右端点
        if(left == right && nums[right] == target){ ret[1] = right; }
       
        return ret;
    }
};

---

总结查找区间左端点的模板

while(left < right)
{
    int mid = left + (right - left) / 2;
    if(......) { left = mid + 1; }
    else{ right = mid; }
}

总结查找区间右端点的模板

while(left < right)
{
    int mid = left + (right - left + 1) / 2;
    if(......) { right = mid - 1; }
    else { left = mid; }
}

记忆方法：下面出现 -1 的时候，上面求 mid 就 +1；分类讨论的代码，就题论题即可.

---

题目3：69. x 的平方根 - 力扣（LeetCode）

题目分析

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意： 不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

"不允许使用任何内置指数函数和算符"说明使用时需要自己实现这些函数。

---

题目示例

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

---

算法原理

示例：x = 17

解法1：暴力解法

暴力解法就是从1往后依次尝试，直到某个数的平方大于等于x，如果等于x，则返回当前值，如果大于，则返回前一个值。

解法2：二分查找算法

观察1~9的平方，我们可以知道这是递增的，需要观察是否存在二段性。

由结果来分析答案，x = 17时，返回的是4；x = 36时，返回的是6。返回的数的平方值都是小于等于 x。

将序列抽象化：

ret 的左边的数的平方都是小于等于 ret 的平方，ret 的右边的数平方都是大于 ret 的平方。

定义 left 和 right，left从1开始，right 从 x 开始，中间数 mid，看中间 mid 的平方值落在哪个区间。

如果 mid*mid <= x，则在 [mid, right] 区间中找，更新 left，让 left = mid，因为有可能 mid 所在的位置的值就是目标值。如果 mid*mid > x，则在 [left, mid] 区间中找，更新 right，让 right = mid -- 1，越过 mid 所在位置的值，为什么？因为目标值的平方一定是小于等于x，mid 的平方都大于 x 了，那么 mid 所在的位置的值一定不是目标值。

---

代码实现

class Solution {
public:
    int mySqrt(int x) {
        // 考虑 x 小于1的情况
        if(x < 1)
        {
            return 0;
        }
        // 定义left和right指针
        int left = 1, right = x;

        while(left < right)
        {
            // 计算mid,x可能很大
            long long mid = left + (right - left + 1) / 2;
            // 若pow(mid) <= x,left = mid
            if(mid * mid <= x) { left = mid; }
            // 若pow(mid) > x,right = mid - 1
            else { right = mid - 1; }
        }

        return left;
    }
};

---

题目4：35. 搜索插入位置 - 力扣（LeetCode）

题目分析

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

---

题目示例

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 为 无重复元素 的 升序排列数组
• -104 <= target <= 104

---

算法原理

找二段性：本道题有两个情况，可以找到目标值，找不到目标值。

对于找不到目标值的情况，需要找到它的插入位置，它的插入位置可能在第一次出现大于 target 的数的前面，或者整个数组的最后面（由示例2和示例3可以得出）。因此我们要找的位置的值，是大于等于 target 的，大于是找不到，返回插入位置；等于是找到了，返回所在位置。所以可以将序列nums 分成两部分。

最后只需返回大于等于 target 区间的左端点即可。

接下来考虑 left 和 right 的移动：

设 mid 所在位置的值为 x，若x < target，则 target 在 [mid, right] 区间，left = mid + 1；若 x >= target，则 target 在 [left, mid] 区间，right = mid。

---

代码实现

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;

        while(left < right)
        {
            int mid = left + (right - left) / 2;
            int x = nums[mid];

            // 若 x < target,left = mid + 1
            if(x < target) 
            { 
                left = mid + 1; 
            }
            // 若 x >= target,right = mid
            else { right = mid; }
        }

        // 如果target不存在nums,且插入的位置为数组的末端,返回left+1
        return nums[left] < target ? left + 1 : left;
    }
};

---

题目5：852. 山脉数组的峰顶索引 - 力扣（LeetCode）

题目分析

给定一个长度为 n 的整数 山脉 数组 arr ，其中的值递增到一个 峰值元素 然后递减。

返回峰值元素的下标。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

---

题目示例

示例 1：

输入：arr = [0,1,0]
输出：1

示例 2：

输入：arr = [0,2,1,0]
输出：1

示例 3：

输入：arr = [0,10,5,2]
输出：1

提示：

• 3 <= arr.length <= 105
• 0 <= arr[i] <= 106
• 题目数据 保证 arr 是一个山脉数组

---

算法原理

示例：arr = [ 0,1,2,3,2,1,0 ]

将数组 arr 抽象成一个折线：

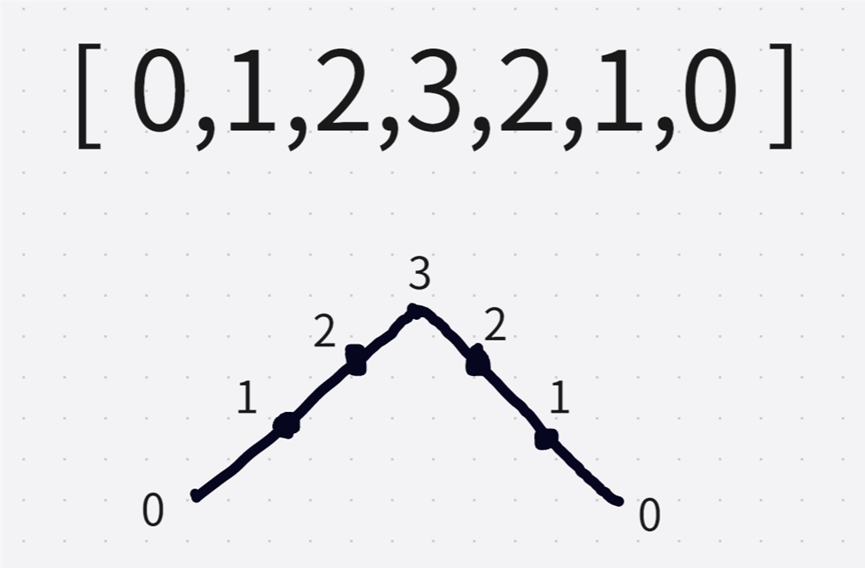
我们可以知道 arr 数组最左边的元素和最右边的元素是不需要考虑的，一定不是峰值。

解法1：暴力解法

定义一个指针 cur，cur 指向的元素与 cur+1 指向的元素进行比较，如果 cur < cur + 1，则 cur++；如果 cur > cur + 1，则当前 cur 指向的位置就是峰值。

解法2：二分查找

将 arr 数组抽象成折线之后，就天然的被分割成了两部分，峰值 ret 的左边，后一个数大于前一个数，峰值 ret 的右边，后一个数小于前一个数。用代码描述，ret的左边：arr[i] > arr[i - 1]，ret的右边：arr[i] < arr[i-1]。

接下来考虑 left 和 right 的移动：

若 arr[mid] > arr[mid - 1]，说明当前趋势在递增，因此目标一定在 mid 右区间，left = mid；若 arr[mid] < arr[mid -- 1]，说明当前趋势在递减，因此目标区间一定在 mid 的左区间，right = mid -- 1。

---

代码实现

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        // 定义两个指针
        // arr 数组的第一个位置和最后一个位置一定不是峰值
        // 因此left从下标1位置开始，right从下标 n - 2 位置开始
        int left = 1, right = arr.size() - 2;

        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            // arr[mid] > arr[mid - 1],left = mid
            if(arr[mid] > arr[mid - 1]) { left = mid; }
            // arr[mid] < arr[mid - 1]),right = mid + 1
            else { right = mid - 1; }
        }

        return left;
    }
};

---

题目6：162. 寻找峰值 - 力扣（LeetCode）

题目分析

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n)的算法来解决此问题。

---

题目示例

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

提示：

• 1 <= nums.length <= 1000
• -231 <= nums[i] <= 231 - 1
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]

---

算法原理

解法1：暴力解法

定义一个指针 cur，如果一直 cur > cur + 1，说明一直下降，则第一个元素就是峰值；如果一直 cur < cur + 1，说明一直上升，则最后一个元素就是峰值；如果 cur < cur + 1，之后 cur > cur + 1，那么当前 cur 就是峰值。

总结：从第一个位置开始，一直向后移动，分情况讨论。

解法2：二分查找

将 nums 抽象成一根线：

分情况讨论 i 和 i+1 位置的值。

若 nums[i] > num[i + 1]，说明此时是一个下降的趋势，那么在 i 的左边区域一定存在峰值，i+1 的右边区域是不确定是否存在峰值，因此可以去 i 的左区域寻找峰值。

若 nums[i] < nums[i + 1]，说明此时是一个上升的趋势，那么在 i+1 的右区域一定存在峰值，i 的左区域不确定是否存在峰值，因此可以去 i+1 的右区域寻找峰值。

根据上述情况的讨论，可以发现 nums 是存在二段性的，因此可以使用二分查找解决问题。

接下来考虑 left 和 right 的移动：

若 nums[mid] > nums[mid + 1]，right = mid；若nums[mid] < nums[mid + 1]，left = mid + 1。

---

代码实现

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        // 定义left和right指针
        int left = 0, right = nums.size() - 1;

        while(left < right)
        {
            int mid = left + (right - left) / 2;
            // 若 nums[mid] > nums[mid + 1],right = mid
            if(nums[mid] > nums[mid + 1]) { right = mid; }
            // 若 nums[mid] < nums[mid + 1],left = mid + 1
            else { left = mid + 1; }
        }

        return left;
    }
};

---

题目7：153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

题目分析

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

理解题目的旋转操作是什么。"注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]]"说明旋转操作是是将数组的最后一个元素移到起始位置。"元素值 互不相同 的数组 nums"说明 nums 中没有相同的元素。

---

题目示例

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

---

算法原理

在未旋转之前，nums 数组是升序的数组，在旋转之后，nums 数组中大的元素都移动到前面。

可以将旋转后的 nums 数组抽象成折线，以 [3,4,5,1,2] 为例：

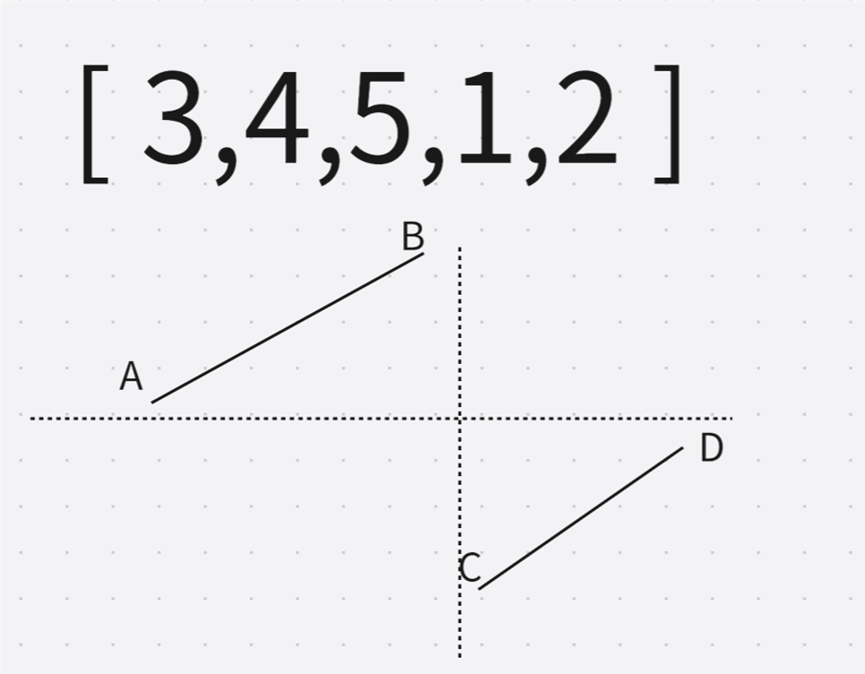
可知 nums 数组存在明显的二段性，因此可以使用二分查找算法解决问题。

---

以 D点(nums数组最后一个元素) 为参照点，很明显 A~B 区域的所有元素都大于 D 点位置的值，C~D 区域的所有元素都是小于等于 D 点位置的值。C~D 区域的 C 点位置的值就是目标值。

A~B区域的特点：nums[i] > nums[n -- 1]；C~D区域的特点：nums[i] <= num[n -- 1]。

接下来考虑 left 和 right 的移动：

若 nums[mid] > nums[right]，说明峰值在 mid 的右区间，left = mid + 1；若 nums[mid] <= nums[right]，说明峰值在 mid 的左区间，right = mid。

代码实现

class Solution {
public:
    int findMin(vector<int>& nums) {
        //定义 left 和 right指针
        int left = 0, right = nums.size() - 1;

        while(left < right)
        {
            以 D 点为参照点
            int mid = left + (right - left) / 2;
            // nums[mid] > nums[right],left = mid + 1
            if(nums[mid] > nums[right]) { left = mid + 1; }
            // nums[mid] <= nums[right],right = mid
            else { right = mid; }
        }

        // 返回目标值
        return nums[right];
    }
};

---

以 A 点作为参照点也可以解决问题。

以A点为参考点，如果只是单纯的 nums[mid] 与 nums[left] 比较是找不到峰值，因为 left 移动后，比较值 nums[left] 不再可靠。

可以转换思想，A~B区域的元素都大于C~D区域的元素，目标值是 C 点，而 C 点有什么特点？C点是第一个小于 A 点的。因此问题就转变成了找第一个小于 nums[0] 的元素，所以我们需要将nums[mid] 应该与nums[0] 比较。

接下来考虑 left 和 right 的移动：

若nums[mid] < nums[0]，往 mid 的左区间找，right = mid；若nums[mid] >= nums[0]，往 mid 的右区间找，left = mid + 1。

细节处理：能使用二分查找算法的前提是序列有二分性，如果 nums 只有一个元素，或者 nums 没有旋转，那么峰值就是nums[0]。

代码实现

class Solution {
public:
    int findMin(vector<int>& nums) {
        // 记录nums的第一个元素
        int target = nums[0];
        int n = nums.size();
        // 如果数组只有一个元素，或未旋转（升序），直接返回
        if (n == 1 || nums[n - 1] >= target) { return target; }

        // 二分查找：找第一个小于 target 的元素
        int left = 0, right = n - 1;
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            // nums[mid] < target,往左区间找
            if (nums[mid] < target) { right = mid; } 
            // nums[mid] >= target,往右区间找
            else { left = mid + 1; }
        }

        // 返回目标值
        return nums[left];
    }
};

推荐使用以 D 点为参考点解决问题。

---

题目8：LCR 173. 点名 - 力扣（LeetCode）

题目分析

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

---

题目示例

示例 1：

输入：records = [0,1,2,3,5]
输出：4

示例 2：

输入：records = [0, 1, 2, 3, 4, 5, 6, 8]
输出：7

---

算法原理

这道题可以使用多种解法，本文使用二分查找算法解决该问题。

示例：records = [0,1,2,3,5,6]

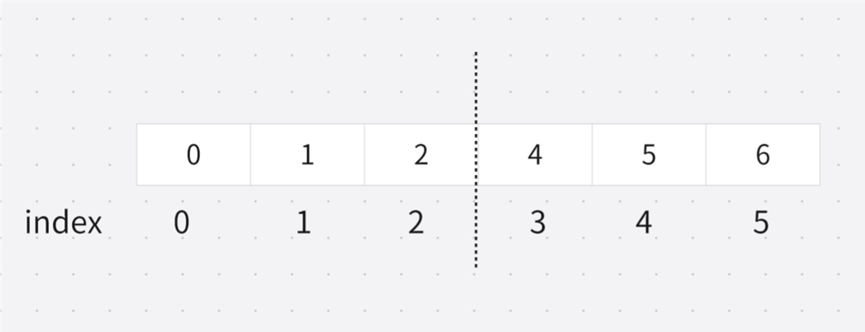
虚线的左侧，元素与下标一一对应；虚线的右侧，元素与下标不一一对应。我们的目标值就是右侧区域左端点的下标。数组存在二分性，可以使用二分查找算法。

接下来考虑 left 和 right 的移动：

若 records[mid] == mid，left = mid + 1；若 records[mid] != mid，right = mid。

细节处理：需要考虑一种特殊情况：records = [0,1,2,3]，元素与下标一一对应，但是它缺少的数是4。这种情况使用二分查找，根本不存在右区间。因此在返回时需要判断 records[n-1] 是否等于 n -- 1，如果相等，则缺失的数字是 n，如果不相等缺失的数字就是 left。

---

代码实现

class Solution {
public:
    int takeAttendance(vector<int>& records) {
        // 定义两个指针
        int left = 0, right = records.size() - 1;
        // records 中最后一个元素的下标
        int n = records.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            // 若 records[mid] == mid,left = mid + 1
            if(records[mid] == mid) { left = mid + 1; }
            // 若 records[mid] != mid,right = mid
            else { right = mid; }
        }

        // 考虑records = [0,1,2,3] 的情况
        return records[n] == n ? n+1 : left;
    }
};

---