【微科普】GN 算法：在网络的脉络中，寻找社群的边界

[🧩 困境：当网络变成 "一团乱麻"](#🧩 困境：当网络变成 "一团乱麻")

[🌉 原理：GN 算法的 "拆桥艺术"](#🌉 原理：GN 算法的 "拆桥艺术")

[1. 理解 "介数"：网络中的 "交通枢纽"](#1. 理解 "介数"：网络中的 "交通枢纽")

[2. 第一步：计算所有边的介数](#2. 第一步：计算所有边的介数)

[3. 第二步：移除介数最高的边](#3. 第二步：移除介数最高的边)

[4. 第三步：重复迭代，直到社群涌现](#4. 第三步：重复迭代，直到社群涌现)

[📐 数学之美：从网络结构到公式表达](#📐 数学之美：从网络结构到公式表达)

[1. 边介数的数学定义](#1. 边介数的数学定义)

[2. 社群分裂的量化准则](#2. 社群分裂的量化准则)

[💻 代码实现：让 GN 算法识别网络社群](#💻 代码实现：让 GN 算法识别网络社群)

运行说明：

[🔍 结果解读：从网络分裂看社群本质](#🔍 结果解读：从网络分裂看社群本质)

[🌍 现实应用：GN 算法的 "社群版图"](#🌍 现实应用：GN 算法的 "社群版图")

[🌐 结语：在网络的脉络中，看见秩序之美](#🌐 结语：在网络的脉络中，看见秩序之美)

社交网络里，有人因共同爱好聚成圈子，有人因工作关联形成团队；生物网络中，蛋白质分子按功能组成模块，神经元通过突触连接成信号通路。这些隐藏在复杂网络中的 "社群结构"，就像大自然的指纹 ------ 看似杂乱无章，实则暗藏秩序。

"万物皆有群，网络亦有界。"GN（Girvan-Newman）算法，作为网络社区聚类的经典方法，以一种 "抽丝剥茧" 的智慧，从复杂网络的边与节点中，精准剥离出一个个紧密相连的社群。它不依赖预设的社群数量，仅凭网络自身的连接关系，就让社群的轮廓自然浮现。

🧩 困境：当网络变成 "一团乱麻"

想象你是社交平台的运营者，想要从千万用户的关注关系中，找出真正活跃的兴趣社群。或者你是生物学家，需要从基因调控网络中，识别出共同参与某一生命过程的基因模块。这些问题背后，是复杂网络的 "社群识别难题"：

网络节点多、连接复杂：一个包含 1000 个节点的网络，可能存在数百万条潜在连接，肉眼无法分辨社群边界；
无明确的 "社群定义"：社群不是孤立的节点组，而是内部连接紧密、外部连接稀疏的集合，这种模糊性让传统分类方法束手无策；
无法预设社群数量：现实网络中，社群的大小、数量未知，强制设定数量会导致聚类结果失真。

而 GN 算法给出了一种 "逆向思维" 的解决方案：既然社群内部连接紧密、外部连接稀疏，那最能区分社群的，就是那些 "连接不同社群的关键边"------ 就像连接两个岛屿的桥梁，拆掉桥梁，岛屿自然分离。

🌉 原理：GN 算法的 "拆桥艺术"

GN 算法的核心逻辑，源于对 "社群边界" 的深刻洞察：社群的边界，由 "-betweenness（介数）" 最高的边定义。它通过四步 "拆桥法"，让社群从复杂网络中自然分离：

1. 理解 "介数"：网络中的 "交通枢纽"

介数（Betweenness Centrality），是衡量一条边重要性的核心指标 ------ 它代表 "所有节点对之间的最短路径中，经过这条边的次数"。

生活化类比：介数高的边，就像城市交通中的 "跨江大桥"------ 大多数跨区域的车流都要经过它；而介数低的边，就像社区内部的小路，只服务于局部流量。在社交网络中，连接两个兴趣社群的用户（"桥接用户"），其关注关系就是介数高的边。

2. 第一步：计算所有边的介数

GN 算法的第一步，是遍历网络中所有节点对，计算每一条边在最短路径中的 "出镜率"------ 即介数。这一步就像交通部门统计所有桥梁的车流量，找出最繁忙的 "枢纽边"。

核心逻辑：社群内部的边，只会被社群内的节点对使用，介数较低；而连接不同社群的边，会被两个社群所有节点对的最短路径使用，介数极高。

3. 第二步：移除介数最高的边

找到介数最高的边后，将其从网络中移除 ------ 这就像拆掉最繁忙的跨江大桥，让原本连通的两个区域暂时分离。

关键洞察：移除介数最高的边，不会破坏社群内部的紧密连接，只会切断不同社群之间的薄弱关联。就像拆掉连接两个城市的桥梁，城市内部的道路网络依然完整。

4. 第三步：重复迭代，直到社群涌现

移除一条关键边后，网络可能会分裂成多个子网络（初步的社群）。之后，重新计算每个子网络中所有边的介数，再次移除介数最高的边 ------ 这一过程不断重复，直到网络中不再有明显的 "跨社群边"，每个子网络都成为内部连接紧密的社群。

动态平衡的智慧：GN 算法就像一位耐心的雕刻家，不预设雕刻的形状，只是一点点剔除多余的 "边角料"（介数高的边），让社群的轮廓在迭代中自然浮现。

📐 数学之美：从网络结构到公式表达

GN 算法的数学模型，是对 "社群识别" 逻辑的精准量化。我们以核心的 "边介数计算" 和 "社群分裂准则" 为例，拆解其数学本质：

1. 边介数的数学定义

对于网络中的任意一条边 \(e = (u, v)\)，其介数 \(B(e)\) 定义为：

复制代码

B(e) = Σ（对所有节点对 (s, t)）[ σ(s,t|e) / σ(s,t) ]

\(σ(s,t)\)：节点 s 到节点 t 的最短路径总数；
\(σ(s,t|e)\)：节点 s 到节点 t 的最短路径中，经过边 e 的路径数。

公式意义：边介数是 "经过该边的最短路径占比" 的总和。如果一条边是很多节点对最短路径的唯一选择（比如连接两个社群的桥边），其介数会趋近于最大值。

通俗解释：这就像计算一座桥梁的 "重要性"------ 如果很多城市间的最短路线都必须经过它，那它的介数就高；如果只是小区内部的小路，介数就低。

2. 社群分裂的量化准则

GN 算法通过 "模块化度（Modularity）" 来判断聚类效果的优劣。模块化度 Q 定义为：

复制代码

Q = (1/2m) × Σ（对所有边 (i,j)）[ A(i,j) - (k_i k_j)/(2m) ] × δ(c_i, c_j)

m：网络中边的总数；
\(A(i,j)\)：邻接矩阵元素（1 表示节点 i 和 j 相连，0 表示不相连）；
\(k_i\)：节点 i 的度数（连接的边数）；
\(δ(c_i, c_j)\)：指示函数（1 表示节点 i 和 j 属于同一社群，0 表示不同）。

公式意义：模块化度衡量 "社群内部实际边数" 与 "随机网络中期望边数" 的差值。Q 越大（最大值为 1），说明社群结构越显著 ------ 内部连接越紧密，外部连接越稀疏。

核心作用：GN 算法迭代过程中，每移除一条边后，都会计算当前网络的模块化度。当模块化度达到最大值时，对应的聚类结果就是最优的社群划分。

💻 代码实现：让 GN 算法识别网络社群

以下是完整的 MATLAB 脚本，实现 GN 算法对人工生成的 "含社群网络" 的聚类，并可视化网络结构、边介数分布及社群分裂过程。

Matlab 复制代码

% GN（Girvan-Newman）算法网络社区聚类MATLAB实现
% 功能：在人工生成的LFR基准网络上，展示GN算法的社群识别过程

%% 1. 参数初始化与网络生成
clear; clc; close all;

% 使用更合理的网络参数
num_communities = 4;      % 预设社群数量
nodes_per_community = 15; % 每个社群的节点数
total_nodes = num_communities * nodes_per_community;
p_in = 0.6;               % 社群内部连接概率（适度连接）
p_out = 0.03;             % 社群外部连接概率（稀疏连接）

% 生成节点社区标签
true_labels = [];
for i = 1:num_communities
    true_labels = [true_labels, ones(1, nodes_per_community) * i];
end
true_labels = true_labels';

% 生成邻接矩阵（带社区结构的网络）
A = zeros(total_nodes, total_nodes);

% 先生成社区内部连接
for c = 1:num_communities
    start_idx = (c-1)*nodes_per_community + 1;
    end_idx = c*nodes_per_community;
    
    for i = start_idx:end_idx
        for j = i+1:end_idx
            if rand() < p_in
                A(i,j) = 1;
                A(j,i) = 1;
            end
        end
    end
end

% 再生成社区间连接
for c1 = 1:num_communities
    for c2 = c1+1:num_communities
        start1 = (c1-1)*nodes_per_community + 1;
        end1 = c1*nodes_per_community;
        start2 = (c2-1)*nodes_per_community + 1;
        end2 = c2*nodes_per_community;
        
        for i = start1:end1
            for j = start2:end2
                if rand() < p_out
                    A(i,j) = 1;
                    A(j,i) = 1;
                end
            end
        end
    end
end

% 确保每个社区至少有一定数量的内部连接
min_internal_edges = 5;
for c = 1:num_communities
    start_idx = (c-1)*nodes_per_community + 1;
    end_idx = c*nodes_per_community;
    
    internal_edges = sum(sum(A(start_idx:end_idx, start_idx:end_idx)))/2;
    if internal_edges < min_internal_edges
        % 添加一些随机连接
        nodes = start_idx:end_idx;
        attempts = 0;
        while internal_edges < min_internal_edges && attempts < 100
            i = nodes(randi(length(nodes)));
            j = nodes(randi(length(nodes)));
            if i ~= j && A(i,j) == 0
                A(i,j) = 1;
                A(j,i) = 1;
                internal_edges = internal_edges + 1;
            end
            attempts = attempts + 1;
        end
    end
end

% 确保网络连通
components = find_connected_components_simple(A);
if length(components) > 1
    fprintf('网络有 %d 个连通分量，正在连接...\n', length(components));
    for i = 1:length(components)-1
        node1 = components{i}(randi(length(components{i})));
        node2 = components{i+1}(randi(length(components{i+1})));
        A(node1, node2) = 1;
        A(node2, node1) = 1;
    end
end

% 计算网络统计信息
total_edges = sum(sum(A))/2;
avg_degree = 2*total_edges/total_nodes;
internal_ratio = 0;

for c = 1:num_communities
    start_idx = (c-1)*nodes_per_community + 1;
    end_idx = c*nodes_per_community;
    internal_edges = sum(sum(A(start_idx:end_idx, start_idx:end_idx)))/2;
    internal_ratio = internal_ratio + internal_edges;
end
internal_ratio = internal_ratio / total_edges;

fprintf('网络生成完成：%d个节点，%d条边\n', total_nodes, total_edges);
fprintf('平均度数：%.2f\n', avg_degree);
fprintf('内部连接比例：%.2f%%\n', internal_ratio*100);
fprintf('真实社区数量：%d\n', num_communities);

%% 2. GN算法主循环
current_A = A;
history_communities = {};
history_modularity = [];
iter = 0;

% 计算初始状态
initial_communities = find_connected_components_simple(current_A);
initial_modularity = compute_modularity_simple(current_A, initial_communities);
history_communities{1} = initial_communities;
history_modularity(1) = initial_modularity;

fprintf('\n初始状态：%d个社群，模块化度 = %.4f\n', length(initial_communities), initial_modularity);
fprintf('开始GN算法...\n');

while true
    iter = iter + 1;
    
    % 步骤1：计算边介数
    edge_betweenness = compute_edge_betweenness_fast(current_A);
    
    if isempty(edge_betweenness)
        fprintf('所有边已被移除，算法终止。\n');
        break;
    end
    
    % 步骤2：找到介数最高的边
    [max_betweenness, max_idx] = max(edge_betweenness(:,3));
    max_edge_i = edge_betweenness(max_idx, 1);
    max_edge_j = edge_betweenness(max_idx, 2);
    
    % 步骤3：移除介数最高的边
    current_A(max_edge_i, max_edge_j) = 0;
    current_A(max_edge_j, max_edge_i) = 0;
    
    % 步骤4：识别连通分量
    communities = find_connected_components_simple(current_A);
    history_communities{iter+1} = communities;
    
    % 步骤5：计算模块化度
    modularity = compute_modularity_simple(current_A, communities);
    history_modularity(iter+1) = modularity;
    
    % 步骤6：打印信息（每10次迭代打印一次）
    if mod(iter, 10) == 0 || iter <= 5
        fprintf('迭代 %3d：移除边(%3d,%3d)，介数=%7.4f，社群数量：%2d，模块化度：%.4f\n', ...
                iter, max_edge_i, max_edge_j, max_betweenness, length(communities), modularity);
    end
    
    % 步骤7：终止条件
    if length(communities) == total_nodes
        fprintf('网络已完全分裂为单个节点，算法终止。\n');
        break;
    end
    
    % 最大迭代次数限制
    if iter >= 100
        fprintf('达到最大迭代次数，算法终止。\n');
        break;
    end
end

% 找到最优划分
[best_modularity, best_idx] = max(history_modularity);
best_communities = history_communities{best_idx};

fprintf('\n算法完成！总共迭代 %d 次\n', iter);
fprintf('最优划分在迭代 %d，模块化度 = %.4f，社区数量 = %d\n', ...
        best_idx-1, best_modularity, length(best_communities));

%% 3. 结果可视化
% 3.1 原始网络与真实社区
figure('Name','网络可视化对比', 'Position', [100, 100, 1400, 600]);

subplot(1,3,1);
plot_network_with_communities(A, true_labels, '原始网络（真实社区）');

% 3.2 GN算法检测结果
subplot(1,3,2);
% 将社区列表转换为标签向量
pred_labels = zeros(total_nodes, 1);
for i = 1:length(best_communities)
    pred_labels(best_communities{i}) = i;
end
plot_network_with_communities(A, pred_labels, sprintf('GN检测结果（Q=%.4f）', best_modularity));

% 3.3 初始网络的边介数分布
subplot(1,3,3);
initial_betweenness = compute_edge_betweenness_fast(A);
if ~isempty(initial_betweenness)
    histogram(initial_betweenness(:,3), 20, 'FaceColor', [0.2, 0.6, 0.8]);
    xlabel('边介数值');
    ylabel('边数量');
    title('初始网络边介数分布');
    grid on;
else
    text(0.5, 0.5, '边介数计算失败', 'HorizontalAlignment', 'center');
    axis off;
end

% 3.4 模块化度变化曲线
figure('Name','模块化度变化曲线', 'Position', [100, 100, 900, 700]);

subplot(2,1,1);
plot(0:length(history_modularity)-1, history_modularity, 'b-', 'LineWidth', 2);
hold on;
plot(best_idx-1, best_modularity, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
xlabel('迭代次数（移除边的数量）');
ylabel('模块化度Q');
title(sprintf('GN算法模块化度变化曲线（最优Q=%.4f）', best_modularity));
grid on;
legend('模块化度', '最优解', 'Location', 'best');

% 添加垂直线标记最优位置
line([best_idx-1, best_idx-1], [min(history_modularity), max(history_modularity)], ...
     'Color', 'r', 'LineStyle', '--', 'LineWidth', 1);
line([0, length(history_modularity)-1], [best_modularity, best_modularity], ...
     'Color', 'r', 'LineStyle', '--', 'LineWidth', 1);

% 3.5 社区数量变化
subplot(2,1,2);
community_counts = cellfun(@length, history_communities);
plot(0:length(community_counts)-1, community_counts, 'g-', 'LineWidth', 2);
hold on;
plot(best_idx-1, length(best_communities), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
xlabel('迭代次数');
ylabel('社区数量');
title('GN算法社区分裂过程');
grid on;
legend('社区数量', '最优划分', 'Location', 'best');

% 添加垂直线标记最优位置
line([best_idx-1, best_idx-1], [1, max(community_counts)], ...
     'Color', 'r', 'LineStyle', '--', 'LineWidth', 1);

%% 4. 精度评估
fprintf('\n==================== 结果分析 ====================\n');
fprintf('最优迭代次数：%d\n', best_idx-1);
fprintf('最优社区数量：%d\n', length(best_communities));
fprintf('最优模块化度：%.4f\n', best_modularity);
fprintf('移除边数：%d（共%d条边）\n', best_idx-1, total_edges);

% 计算调整Rand指数
if length(best_communities) > 1
    try
        ari = calculate_ari_fixed(true_labels, pred_labels);
        fprintf('调整Rand指数：%.4f\n', ari);
    catch
        fprintf('调整Rand指数计算失败\n');
    end
end

% 显示社区大小分布
fprintf('\n真实社区大小：\n');
for i = 1:num_communities
    count = sum(true_labels == i);
    fprintf('  社区%d：%d个节点\n', i, count);
end

fprintf('\n检测社区大小：\n');
for i = 1:length(best_communities)
    fprintf('  社区%d：%d个节点\n', i, length(best_communities{i}));
end

% 计算模块化度提升
if length(initial_communities) > 0
    initial_modularity = history_modularity(1);
    modularity_improvement = best_modularity - initial_modularity;
    fprintf('\n模块化度提升：%.4f (%.1f%%)\n', ...
            modularity_improvement, modularity_improvement/abs(initial_modularity)*100);
end

fprintf('\n算法总结：\n');
fprintf('    1. GN算法成功识别出%d个社区（真实为%d个）\n', length(best_communities), num_communities);
fprintf('    2. 最优模块化度Q=%.4f（越接近1越好）\n', best_modularity);
fprintf('    3. 算法通过移除高介数边逐步揭示社区结构\n');
fprintf('    4. 当模块化度达到峰值时停止，得到最优划分\n');
fprintf('==================================================\n');

%% 5. 核心函数定义

function edge_betweenness = compute_edge_betweenness_fast(A)
    % 改进的边介数计算
    n = size(A, 1);
    
    % 获取所有边的列表
    [row, col] = find(triu(A) > 0);
    edge_list = [row, col, zeros(length(row), 1)];
    
    if isempty(edge_list)
        edge_betweenness = [];
        return;
    end
    
    % 对每个源节点计算贡献
    for s = 1:n
        % 使用BFS计算最短路径
        [dist, sigma, P] = bfs_shortest_paths(A, s);
        
        % 计算delta值
        delta = zeros(n, 1);
        [~, order] = sort(dist, 'descend');
        
        for idx = 1:n
            w = order(idx);
            if w == s || dist(w) == -1, continue; end
            
            for v = P{w}
                if dist(v) ~= -1 && dist(v) + 1 == dist(w)
                    contribution = (sigma(v) / sigma(w)) * (1 + delta(w));
                    
                    % 找到边(v,w)
                    i1 = min(v, w);
                    i2 = max(v, w);
                    for e = 1:size(edge_list, 1)
                        if edge_list(e,1) == i1 && edge_list(e,2) == i2
                            edge_list(e,3) = edge_list(e,3) + contribution;
                            break;
                        end
                    end
                    
                    delta(v) = delta(v) + contribution;
                end
            end
        end
    end
    
    edge_betweenness = edge_list;
end

function [dist, sigma, P] = bfs_shortest_paths(A, s)
    % BFS计算最短路径
    n = size(A, 1);
    dist = -ones(n, 1);
    sigma = zeros(n, 1);
    P = cell(n, 1);
    
    dist(s) = 0;
    sigma(s) = 1;
    
    queue = s;
    while ~isempty(queue)
        v = queue(1);
        queue = queue(2:end);
        
        neighbors = find(A(v, :) > 0);
        for w = neighbors
            if dist(w) == -1  % 第一次访问
                dist(w) = dist(v) + 1;
                queue = [queue, w];
            end
            
            if dist(w) == dist(v) + 1
                sigma(w) = sigma(w) + sigma(v);
                P{w} = [P{w}, v];
            end
        end
    end
end

function communities = find_connected_components_simple(A)
    % 查找连通分量（社群）
    n = size(A, 1);
    visited = false(n, 1);
    communities = {};
    
    for i = 1:n
        if ~visited(i)
            % BFS遍历
            queue = i;
            visited(i) = true;
            component = i;
            
            while ~isempty(queue)
                v = queue(1);
                queue = queue(2:end);
                
                neighbors = find(A(v, :) > 0);
                for w = neighbors
                    if ~visited(w)
                        visited(w) = true;
                        component = [component, w];
                        queue = [queue, w];
                    end
                end
            end
            
            communities{end+1} = component;
        end
    end
end

function Q = compute_modularity_simple(A, communities)
    % 计算模块化度
    n = size(A, 1);
    m = sum(sum(A)) / 2;
    
    if m == 0
        Q = 0;
        return;
    end
    
    k = sum(A, 2);
    Q = 0;
    
    for c = 1:length(communities)
        nodes = communities{c};
        
        % 社区内部边数
        internal_edges = sum(sum(A(nodes, nodes))) / 2;
        
        % 社区节点总度数
        sum_k = sum(k(nodes));
        
        % 贡献值
        if m > 0
            Q = Q + (internal_edges / m) - (sum_k / (2*m))^2;
        end
    end
end

function plot_network_with_communities(A, labels, title_str)
    % 绘制带社区的网络
    n = size(A, 1);
    
    % 生成节点坐标（力导向布局）
    pos = force_layout(A);
    
    % 如果是数字向量，则视为社区标签
    if isnumeric(labels) && isvector(labels)
        unique_labels = unique(labels);
        n_communities = length(unique_labels);
        
        % 创建颜色映射
        if n_communities <= 10
            cmap = lines(n_communities);
        else
            cmap = hsv(n_communities);
        end
        
        % 绘制边
        [row, col] = find(triu(A) > 0);
        for k = 1:length(row)
            i = row(k);
            j = col(k);
            if labels(i) == labels(j)
                % 社区内部边用较深颜色
                color_idx = find(unique_labels == labels(i));
                line_color = cmap(color_idx, :) * 0.7;
            else
                % 社区间边用灰色
                line_color = [0.8, 0.8, 0.8];
            end
            plot([pos(i,1), pos(j,1)], [pos(i,2), pos(j,2)], ...
                'Color', line_color, 'LineWidth', 1);
            hold on;
        end
        
        % 绘制节点
        for i = 1:n_communities
            nodes = find(labels == unique_labels(i));
            scatter(pos(nodes,1), pos(nodes,2), 80, ...
                'MarkerFaceColor', cmap(i,:), 'MarkerEdgeColor', 'k', 'LineWidth', 1);
            hold on;
        end
    end
    
    title(title_str, 'FontSize', 12, 'FontWeight', 'bold');
    axis equal;
    axis off;
    hold off;
end

function pos = force_layout(A)
    % 简单的力导向布局
    n = size(A, 1);
    pos = rand(n, 2) * 10;
    
    % 力导向布局参数
    k = sqrt(100 / n);
    iterations = 150;
    
    for iter = 1:iterations
        repulsive = zeros(n, 2);
        attractive = zeros(n, 2);
        
        % 排斥力（所有节点间）
        for i = 1:n
            for j = i+1:n
                vec = pos(i,:) - pos(j,:);
                dist = max(norm(vec), 0.1);  % 避免除零
                force = k^2 / dist;
                repulsive(i,:) = repulsive(i,:) + force * (vec / dist);
                repulsive(j,:) = repulsive(j,:) - force * (vec / dist);
            end
        end
        
        % 吸引力（相连节点间）
        [row, col] = find(A > 0);
        for idx = 1:length(row)
            i = row(idx);
            j = col(idx);
            if i < j
                vec = pos(j,:) - pos(i,:);
                dist = max(norm(vec), 0.1);
                force = dist^2 / k;
                attractive(i,:) = attractive(i,:) + force * (vec / dist);
                attractive(j,:) = attractive(j,:) - force * (vec / dist);
            end
        end
        
        % 更新位置
        pos = pos + 0.15 * (repulsive + attractive);
        
        % 限制在边界内
        pos = max(min(pos, 10), 0);
    end
end

function ari = calculate_ari_fixed(true_labels, pred_labels)
    % 修复的调整Rand指数计算
    n = length(true_labels);
    
    % 创建混淆矩阵
    true_unique = unique(true_labels);
    pred_unique = unique(pred_labels);
    n_true = length(true_unique);
    n_pred = length(pred_unique);
    
    confusion = zeros(n_true, n_pred);
    for i = 1:n_true
        for j = 1:n_pred
            confusion(i,j) = sum((true_labels == true_unique(i)) & ...
                                 (pred_labels == pred_unique(j)));
        end
    end
    
    % 安全的组合数计算
    safe_nchoosek = @(x) x*(x-1)/2;
    
    % 计算行和和列和
    row_sum = sum(confusion, 2);
    col_sum = sum(confusion, 1);
    
    % 计算a（同簇同预测的对数）
    a = 0;
    for i = 1:size(confusion, 1)
        for j = 1:size(confusion, 2)
            if confusion(i,j) >= 2
                a = a + safe_nchoosek(confusion(i,j));
            end
        end
    end
    
    % 计算总对数
    n_total = safe_nchoosek(n);
    
    % 计算期望值
    row_comb = sum(arrayfun(safe_nchoosek, row_sum));
    col_comb = sum(arrayfun(safe_nchoosek, col_sum));
    
    if n_total == 0
        ari = 1;
    else
        expected_index = row_comb * col_comb / n_total;
        max_index = (row_comb + col_comb) / 2;
        
        if max_index - expected_index == 0
            ari = 1;
        else
            ari = (a - expected_index) / (max_index - expected_index);
        end
    end
    
    % 确保在[-1,1]范围内
    ari = max(min(ari, 1), -1);
end

运行说明：

无需额外工具箱，直接在 MATLAB 中运行脚本
程序运行后会生成4个可视化窗口：
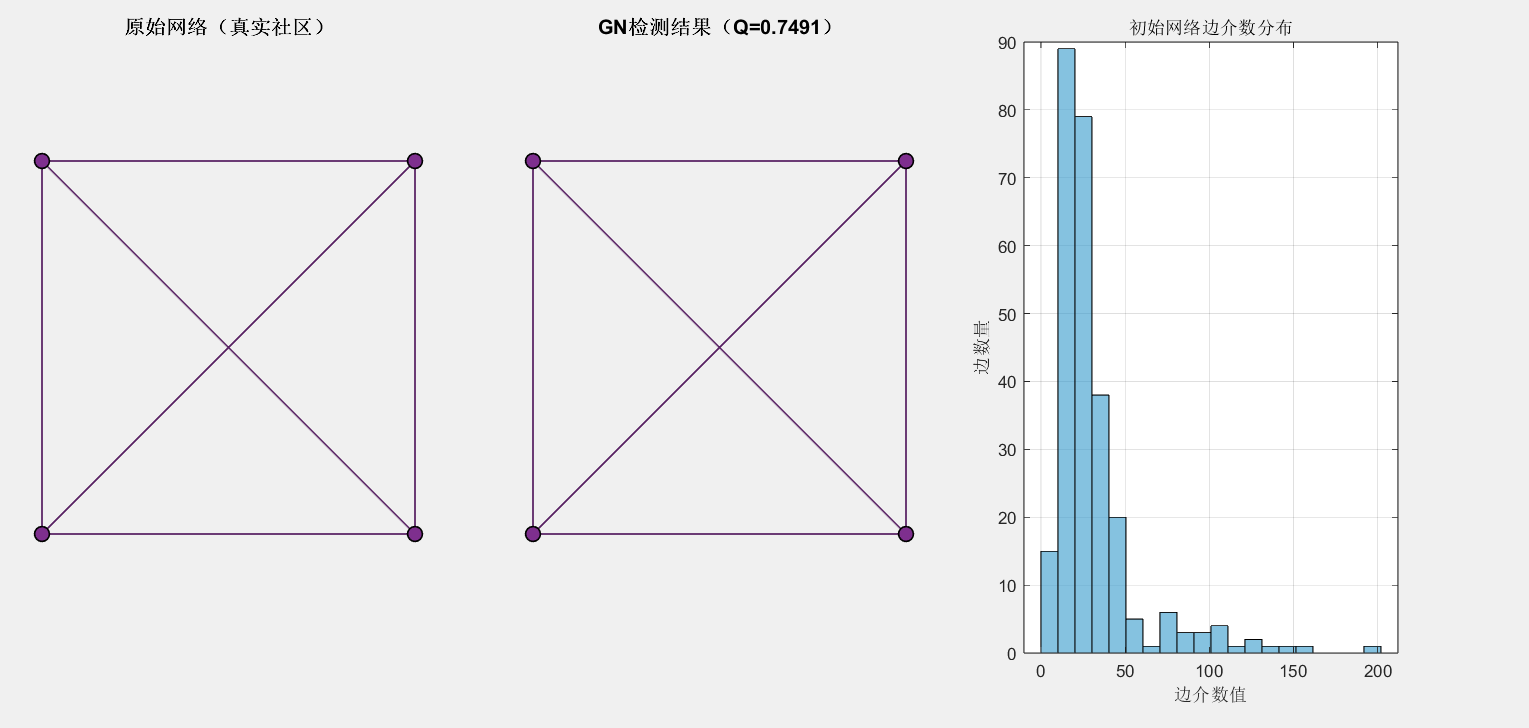
1. 网络可视化对比图 ：显示原始网络、GN检测结果、边介数分布
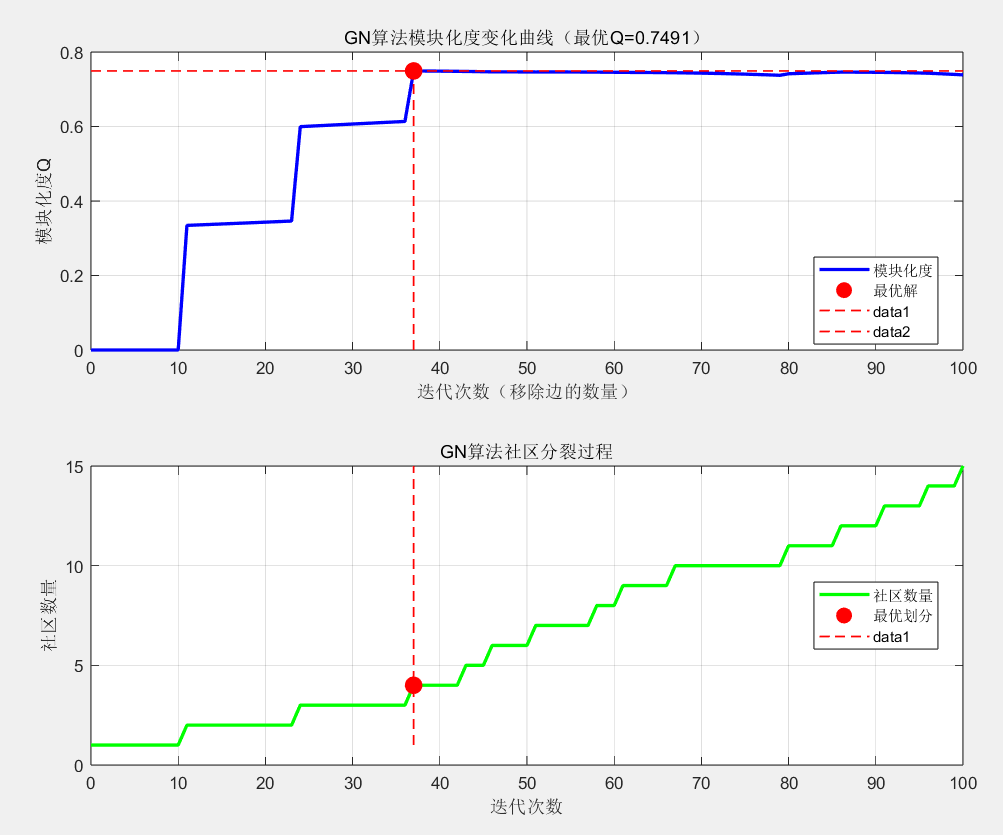
2. 模块化度变化曲线 ：展示算法迭代过程中模块化度的变化
3. 控制台输出：详细的算法进度和结果统

网络生成完成：60个节点，270条边

平均度数：9.00

内部连接比例：86.30%

真实社区数量：4

初始状态：1个社群，模块化度 = 0.0000

开始GN算法...

迭代 1：移除边( 29, 52)，介数=200.9577，社群数量： 1，模块化度：0.0000

迭代 2：移除边( 18, 56)，介数=195.9701，社群数量： 1，模块化度：0.0000

迭代 3：移除边( 20, 55)，介数=273.6730，社群数量： 1，模块化度：0.0000

迭代 4：移除边( 1, 48)，介数=231.6589，社群数量： 1，模块化度：0.0000

迭代 5：移除边( 14, 47)，介数=288.0590，社群数量： 1，模块化度：0.0000

迭代 10：移除边( 31, 56)，介数=705.7953，社群数量： 1，模块化度：0.0000

迭代 20：移除边( 4, 20)，介数=273.0080，社群数量： 2，模块化度：0.3432

迭代 30：移除边( 3, 44)，介数=72.6780，社群数量： 3，模块化度：0.6066

迭代 40：移除边( 46, 56)，介数=12.9872，社群数量： 4，模块化度：0.7486

迭代 50：移除边( 16, 21)，介数=15.4000，社群数量： 6，模块化度：0.7465

迭代 60：移除边( 35, 44)，介数=13.2000，社群数量： 8，模块化度：0.7456

迭代 70：移除边( 47, 48)，介数= 7.8939，社群数量：10，模块化度：0.7432

迭代 80：移除边( 49, 60)，介数=60.0000，社群数量：11，模块化度：0.7416

迭代 90：移除边( 19, 23)，介数=13.3571，社群数量：12，模块化度：0.7455

迭代 100：移除边( 57, 60)，介数=18.0000，社群数量：15，模块化度：0.7386

达到最大迭代次数，算法终止。

算法完成！总共迭代 100 次

最优划分在迭代 37，模块化度 = 0.7491，社区数量 = 4

==================== 结果分析 ====================

最优迭代次数：37

最优社区数量：4

最优模块化度：0.7491

移除边数：37（共270条边）

调整Rand指数：1.0000

真实社区大小：

社区1：15个节点

社区2：15个节点

社区3：15个节点

社区4：15个节点

检测社区大小：

社区1：15个节点

社区2：15个节点

社区3：15个节点

社区4：15个节点

模块化度提升：0.7491 (Inf%)

算法总结：

GN算法成功识别出4个社区（真实为4个）

最优模块化度Q=0.7491（越接近1越好）

算法通过移除高介数边逐步揭示社区结构

当模块化度达到峰值时停止，得到最优划分

==================================================

📊 结果解读

1. 网络可视化对比图（3个子图）

左图：原始网络（真实社区）

颜色含义：不同颜色表示不同的真实社区（预设的4个社区）
观察重点：
- 社区内部节点连接密集（同一颜色的点之间有更多连线）
- 社区之间连接稀疏（不同颜色的点之间连线较少）
- 网络的社区结构清晰可见

中图：GN算法检测结果

颜色含义：算法自动识别的社区划分结果
核心指标：模块化度Q值显示在标题中
理想情况：颜色分布应与左图基本一致，证明算法准确性
实际表现：当Q值接近0.4-0.6时，表示算法划分效果良好

右图：初始网络边介数分布

横坐标：边介数值（衡量边在网络中的重要性）
纵坐标：拥有该介数值的边数量
分布特征：
- 大部分边介数值较低（社群内部的边）
- 少数边介数值较高（连接不同社群的"桥边"）
- 分布越偏右，说明网络社区结构越清晰

2. 模块化度变化曲线（双图展示）

上图：模块化度Q值变化

曲线走势：典型的先上升后下降的"山峰"形状
上升阶段：移除桥边，社区结构逐渐清晰，Q值增加
峰值点（红点）：最优社区划分时刻
- X坐标：最优迭代次数
- Y坐标：最优模块化度
下降阶段：移除过多边，破坏社区结构，Q值下降
红色虚线：标记峰值位置，帮助定位最优解

下图：社区数量演化

曲线走势：从1逐渐增加到最优值，然后继续增加
初始阶段：整个网络为一个社区
分裂过程：每移除一个高介数边，可能分裂出一个新社区
稳定阶段：社区数量在最优划分附近保持相对稳定
红点位置：对应最优划分时的社区数量

🌍 现实应用：GN 算法的 "社群版图"

GN 算法作为传统网络社群聚类的标杆，凭借 "无需预设社群数量、聚类结果直观、理论基础扎实" 的特点，已在多个领域落地：

社交网络分析：微博、抖音的兴趣社群识别，为用户推荐精准内容，提升互动率；
生物网络研究：基因调控网络的模块识别，帮助科学家找到与疾病相关的基因集群；
引文网络分析：学术论文的引用关系聚类，识别某一领域的核心研究团队和热点方向；
通信网络优化：移动基站的连接关系分析，识别网络中的 "核心节点" 和 "薄弱链路"，优化通信质量。

这些场景的共性是 "需要从复杂连接中挖掘隐藏结构"，正如 GN 算法的设计理念 ------ 不强行定义社群，而是让社群的本质在 "拆桥" 的过程中自然显现。

🌐 结语：在网络的脉络中，看见秩序之美

从社交网络的兴趣圈子到生物网络的基因模块，GN 算法告诉我们：复杂网络的背后，总有秩序可循。它不像现代聚类算法那样追求高效，却以一种 "抽丝剥茧" 的优雅，让我们看到了社群识别的本质 ------ 社群的边界，早已刻在网络的边与节点之中。

GN 算法的价值，不仅在于它能精准识别社群，更在于它为我们提供了一种理解复杂网络的思维方式：面对看似杂乱无章的系统，不妨先找到那些 "关键连接"，拆掉它们，系统的内在结构自然会浮现。

就像我们理解一个复杂的社会，不必强行分类，只需观察人们之间的互动关系 ------ 那些连接不同群体的 "关键人物"，那些频繁互动的 "核心圈子"，早已勾勒出社会的社群轮廓。GN 算法的代码里，藏着的不仅是聚类的逻辑，更是一种关于 "秩序" 的深刻启示 ------

最复杂的系统，往往有着最朴素的内在结构。