文章目录
- 一、绪论:关于监督学习
-
- [1. 分类和回归任务](#1. 分类和回归任务)
- [2. 常见监督学习算法](#2. 常见监督学习算法)
- 二、线性回归
-
- [1. 核心公式](#1. 核心公式)
- [2. 损失函数](#2. 损失函数)
- [3. 参数优化:梯度下降原理](#3. 参数优化:梯度下降原理)
- 三、逻辑回归
-
- [1. 线性回归部分](#1. 线性回归部分)
- [2. 激活函数(Sigmoid函数)](#2. 激活函数(Sigmoid函数))
- [3. 完整的逻辑回归公式](#3. 完整的逻辑回归公式)
- [4. 决策边界](#4. 决策边界)
- [5. 损失函数](#5. 损失函数)
人工智能(AI)作为引领科技变革的核心领域,其发展历程跨越七十余年,从早期的理论探索逐步走向规模化工程应用,深刻重塑了各行各业的技术范式。回溯其演进脉络,不仅呈现出理论派系的交替迭代,更在技术落地中形成了以机器学习、深度学习为核心的技术体系,为复杂问题的解决提供了全新思路。
AI的发展可追溯至1956年达特茅斯会议,期间历经四个关键阶段,呈现出连接主义与符号主义两大派系的交替发展格局。符号主义 以逻辑推理和数学原理为基础,强调通过明确的规则与符号表征解决问题;连接主义则模仿生物神经网络的结构与机制,通过数据驱动的方式自主学习模式与规律。两者在发展中曾交替主导:1969年符号主义代表人物明斯基对神经网络的批判,导致连接主义陷入长期低谷;2000年后,随着大数据与计算能力的突破,深度学习的兴起让连接主义重新占据主导地位。而进入2020年代,以ChatGPT为代表的大语言模型成为领域热点,其核心趋势正是试图整合两大派系的优势,既保留连接主义的数据驱动能力,又融入符号主义的逻辑推理特性,推动AI向更通用、更强大的方向演进。
机器学习作为AI的核心分支,是实现数据驱动智能的关键技术 ,其基础理论主要分为三大类型:监督学习、非监督学习与半监督学习。 监督学习依赖带标签数据构建输入与输出的映射函数,适用于分类(如垃圾邮件识别)、回归(如房价预测)等明确目标的任务;非监督学习则利用无标签数据自主发现隐藏的结构与模式,典型应用包括聚类分析、数据降维与异常检测;半监督学习则介于两者之间,通过少量标签数据辅助无标签数据训练,有效解决了标注成本过高的问题(如ImageNet数据集的扩充场景)。
深度学习作为机器学习的重要延伸,尤其擅长处理大规模数据与复杂模式识别任务,已成为当前AI应用的核心技术支撑。 其理论基础建立在神经网络之上,核心概念涵盖神经元、激活函数、前向传播与反向传播机制,而损失函数与优化器则是模型训练的关键组件------不同优化器的策略差异直接影响模型的收敛效率与泛化能力。此外,经典神经网络架构(如卷积神经网络CNN)、基础网络层的设计,以及深度学习框架生态的演变(从早期的TensorFlow到大语言模型时代的新型框架),共同构成了深度学习技术落地的完整链路。
一、绪论:关于监督学习
监督学习核心在于通过带标签的训练数据,让模型学会输入与输出之间的映射关系。常见算法包括线性回归、逻辑回归、决策树、随机森林等。线性回归通过最小二乘法优化损失函数,适用于房价预测等连续数值预测任务。多变量线性回归需进行特征缩放以避免数值差异过大影响模型训练。监督学习广泛应用于垃圾邮件检测、车牌识别、情感分析等场景。
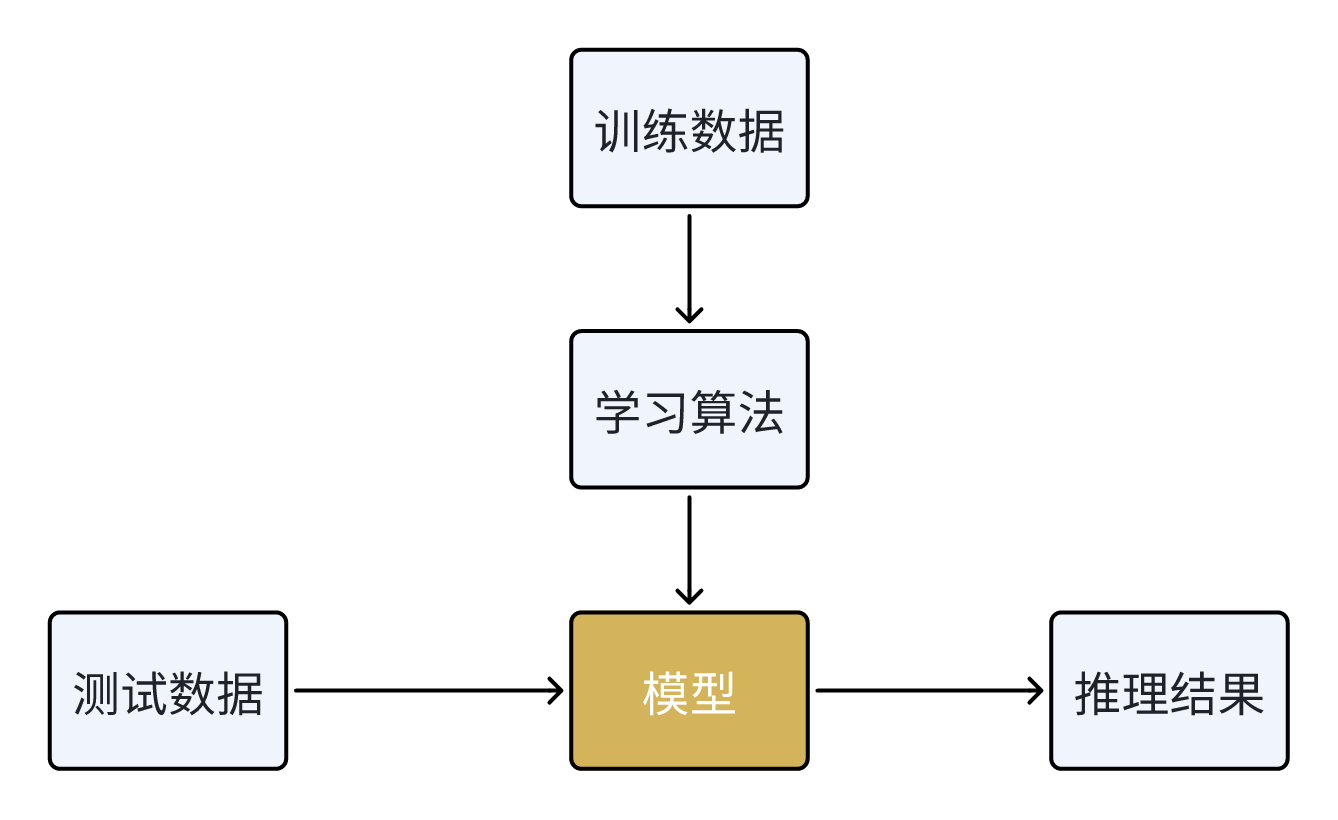
在监督学习中,训练数据是带标签的,也就是说,每个输入数据都有一个对应的输出标签。模型的目标是从这些输入数据和标签对中学习一个映射函数,使得给定新的输入时,能够预测出正确的输出标签。
- 输入数据(X):由特征组成的样本数据。
- 输出标签(y):与输入数据对应的正确答案(标签) ,如价格、类别、销售额等。
1. 分类和回归任务
分类任务主要用于离散标签的预测,如情感分析、垃圾邮件检测、手写数字识别等。
回归任务主要用于连续数值的预测,如房价预测、股票预测等。
2. 常见监督学习算法
- 线性回归 是最简单的监督学习算法之一,用于回归问题,通过最小二乘法进行优化。
- 逻辑回归 是线性回归的扩展,用于分类问题,通过逻辑函数进行转换。
- 决策树 是一种简单的监督学习方法,通过树状结构进行决策,适用于分类和回归任务。
- 随机森林 是决策树的升级版本,通过多棵树进行投票,提高分类准确性。
- 感知器和深度神经网络 也属于监督学习算法,通过大量训练数据进行学习,适用于分类和回归任务。
- 除了以上算法,常见的监督学习算法还包括:最近邻算法、朴素贝叶斯、支持向量机等。
二、线性回归
线性回归是监督学习中用于预测连续型目标变量的基础模型,核心思想是通过构建自变量与因变量之间的线性关系,拟合数据并实现预测。
- 线性回归使用线性方程来捕捉自变量和因变量之间的关系,通过最小二乘法进行优化;
- 单变量线性回归:自变量和因变量都是标量,使用最小二乘法(损失函数)进行优化;
- 多变量线性回归:自变量和因变量都是向量,使用向量化的形式进行优化;
- 梯度下降是优化目标函数的方法,通过不断调整模型权重来最小化损失值。
1. 核心公式
(1)简单线性回归(单变量)
当只有一个自变量 ( x ) 时,线性回归假设因变量 ( y ) 与 ( x ) 满足线性关系:

模型的预测值为:
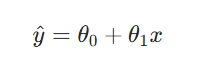
(2)多元线性回归(多变量)
当有 ( n ) 个自变量 ( x_1, x_2, ..., x_n ) 时,线性关系扩展为:
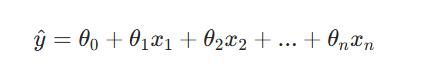
用向量形式简化表示(更便于计算):

2. 损失函数
线性回归的目标是找到最优的参数θ ,使预测值尽可能接近真实值。为此需要定义损失函数(Loss Function),量化预测误差。
线性回归最常用的损失函数是均方误差(Mean Squared Error, MSE),此外也会用到其变体(如残差平方和),少数场景下会使用平均绝对误差(MAE)。
对于 ( m ) 个样本,MSE 计算预测值与真实值误差的平方均值:
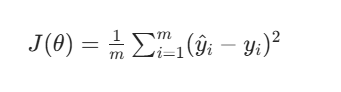
为了后续求导简便,也常引入系数1/2(求导后平方项系数会抵消):
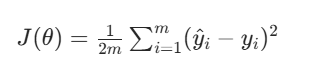
为什么要用平方:为了不偏上或偏下,取平方才能在中间
为什么要2n分之一:求导之后前面会多一个2,因此加一个2分母抵消
3. 参数优化:梯度下降原理
找到最优参数θ的核心是最小化损失函数J(θ),常用方法有两种:
-
解析解(正规方程):直接通过矩阵运算求解以下公式(适用于样本量小、特征少的场景);
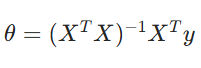
-
数值解(梯度下降):通过迭代优化逼近最优解(适用于样本量大、特征多的场景,如机器学习工程实践)。
梯度下降是一种迭代优化算法,核心逻辑是:
- 初始化参数θ(如随机值或全0);
- 计算损失函数关于 θ的梯度(即偏导数),梯度方向是损失函数上升最快的方向;
- 沿梯度的反方向更新参数(使损失函数减小);
- 重复步骤2-3,直到损失函数收敛(变化量小于阈值)或达到最大迭代次数。
梯度的计算(偏导数推导)

参数更新规则
梯度下降的参数更新公式为:

三、逻辑回归
逻辑回归虽然名字叫"回归",但实际上是一个分类算法。它主要用于二分类问题,比如:
- 邮件是垃圾邮件还是正常邮件?
- 客户是否会购买产品?
- 病人是否患有某种疾病?
逻辑回归的核心思想是:将线性回归的结果通过一个函数转换,使其输出在0-1之间,表示概率。
1. 线性回归部分
首先,我们有一个线性函数:
z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
用矩阵形式表示:
z = w^T x + b
其中:
- w 是权重向量
- x 是特征向量
- b 是偏置项
2. 激活函数(Sigmoid函数)
线性回归的输出可以是任意实数,但我们需要0-1之间的概率值。这里使用Sigmoid函数:
σ(z) = 1 / (1 + e^(-z))
这个函数的特点:
- 输入:任意实数
- 输出:0-1之间的值
- 形状:S形曲线
3. 完整的逻辑回归公式
P(y=1|x) = σ(w^T x + b) = 1 / (1 + e(-(wT x + b)))
输入特征 x → 线性变换 z = w^T x + b → Sigmoid函数 → 概率输出 P(y=1|x)
Sigmoid函数图像:
- 当 z 很大时,σ(z) 接近 1
- 当 z 很小时,σ(z) 接近 0
- 当 z = 0 时,σ(z) = 0.5
4. 决策边界
逻辑回归的决策规则:
- 如果 P(y=1|x) ≥ 0.5,预测为类别1
- 如果 P(y=1|x) < 0.5,预测为类别0
由于 σ(z) = 0.5 时,z = 0,所以决策边界是:w^T x + b = 0
5. 损失函数
逻辑回归使用对数似然损失函数(Log Loss):
L = -[y * log(ŷ) + (1-y) * log(1-ŷ)]
其中:
- y 是真实标签(0或1)
- ŷ 是预测概率
为什么使用这个损失函数?
- 当预测正确时,损失接近0
- 当预测错误时,损失很大
- 对概率预测很敏感