
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 高精度加法](#1. 高精度加法)
[2. 高精度减法](#2. 高精度减法)
[3. 高精度乘法](#3. 高精度乘法)
[4. 高精度除法](#4. 高精度除法)
前言
当数据范围极其之大,甚至超过了long long的存储范围时,我们需要利用字符串来进行加减乘除的运算。因此我们需要先利用字符串存储数据,随后模拟数学中加减乘除的过程。这一算法称之为大数运算,也就是高精度运算
1. 高精度加法
题目链接:
算法原理
我们会发现数据范围为10的18次方,对于这么大的数字,我们利用整型来存储肯定是不合适的,因此得用字符串,也就是string存储,然后进行加法
那么如何进行字符串之间的加法?我们回想小学学过的竖式乘法
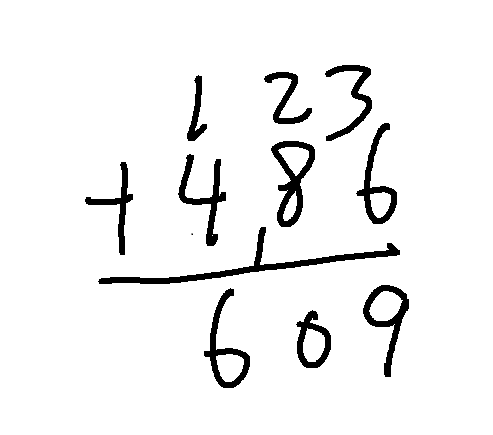
首先便是对应位相加,例如上面6 + 3得9,2+8得10,注意此时相加的10已经超过9了,我们得处理进位,因此留下0,在1+4中需要加上进位1得6,最后得到609。
此时有个小细节,即相加是从最低位开始的,即个位相加后再十位相加
那么对于字符串"123"和"486"相加,我们也得从最后面,即3和6相加开始,但是从后往前加有点不爽,这里我选择把两个字符串倒置,得到"321"和"684",这样从每个字符串开头相加就可以了,得到字符串"906",此时结果字符串仍是倒置的,我们再次倒置得到"609"即可
实操代码
cpp
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main()
{
string a, b; cin >> a >> b;
reverse(a.begin(), a.end());//倒置两个字符串
reverse(b.begin(), b.end());
int forward = 0;//初始时进位设置为0
int left = 0;
string ret;
int i = 0;
while (i < a.size() || i < b.size())
{
int n = 0; int m = 0;
if (i < a.size())
n = a[i] - '0';
if (i < b.size())
m = b[i] - '0';
left = (n + m + forward) % 10;//处理余数
ret += left + '0';
forward = (n + m + forward) / 10;;//处理进位
i++;
}
if (forward)//别忘了处理最后的进位
ret += forward + '0';
reverse(ret.begin(), ret.end());
cout << ret;
return 0;
}2. 高精度减法
题目链接:
算法原理
跟小学数学一样,我们模拟竖式减法即可
但过程中如果第一个数小于第二个数,可能会出现减法。这里为了方便,我们始终让大数减去小数得到正数,如果第一个数较小,最后多加个负号即可
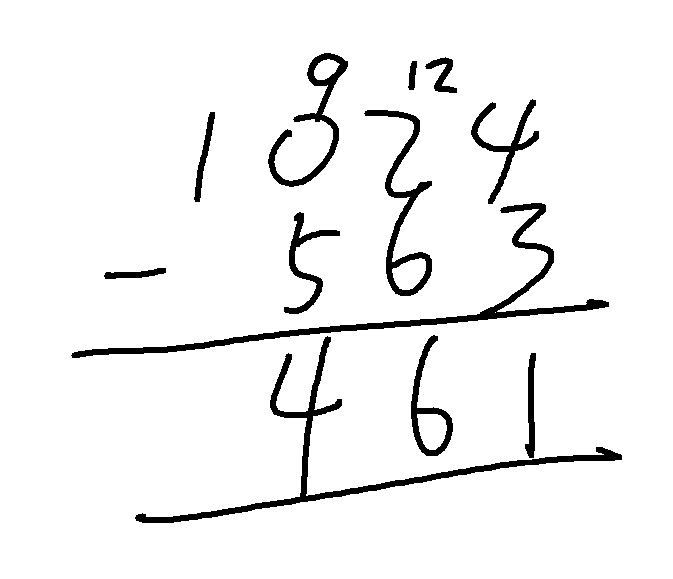
依然是从个位开始,对应位相减,如果不够,那么从高位借一即可
实操代码
cpp
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main()
{
string a, b; cin >> a >> b;
string ret;
if (b.size() > a.size() || (a.size() == b.size() && a < b))
{
cout << "-";
swap(a, b);//保持较大数减较小数
}
reverse(a.begin(), a.end());
reverse(b.begin(), b.end());
int i = 0;
while (i < a.size() || i < b.size())
{
int n = 0; int m = 0;
if (i < a.size())
n = a[i] - '0';
if (i < b.size())
m = b[i] - '0';
int left = n - m;
if (left < 0)
{
left += 10;//向高位借1
a[i + 1]--;
}
ret += left + '0';
i++;
}
reverse(ret.begin(), ret.end());
auto it = ret.begin();
while (it != ret.end() && *it == '0')
it++;
if (it == ret.end())
cout << "0";
else
{
while (it != ret.end())
{
cout << *it;
it++;
}
}
return 0;
}3. 高精度乘法
题目链接:
算法原理
依然是模拟小学的竖式相乘,但较麻烦的是,乘法很容易出现二位数,因此需要频繁地进行进位处理,这里为了方便,我们不进位,到最后相乘完再进位
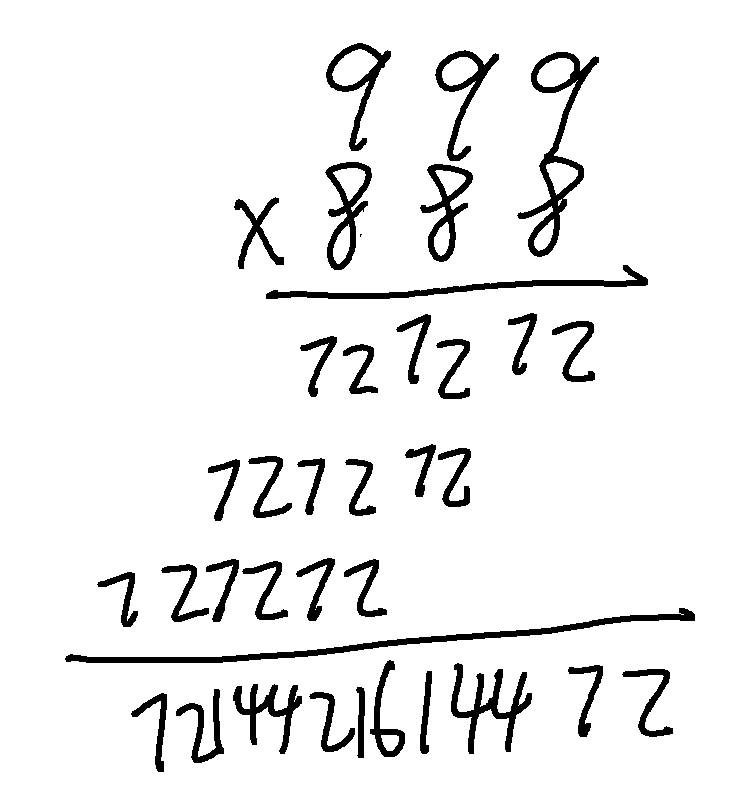
例如在这里,我们不进行进位操作,对于每一位我们直接相加得到最后的结果,最后再进位
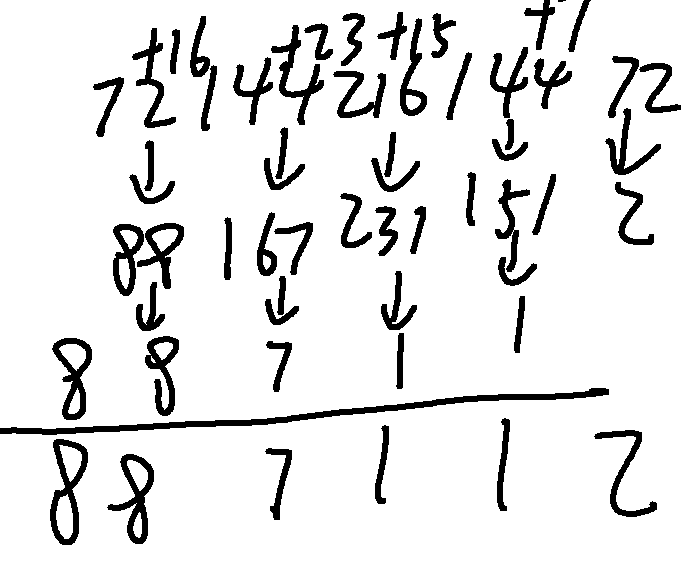
当然也有个小细节,相乘的结果估计会很大,我们需要预设一个较大的数组来存储,但是这样也有可能导致数组有部分空间是空出来的,最后得到的字符串前面会有很多无效0,例如0000887112,因此我们需要在最后去除这些前导0
实操代码
cpp
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
string a, b; cin >> a >> b;
vector<int> v(a.size() + b.size(), 0);
reverse(a.begin(), a.end());
reverse(b.begin(), b.end());
for (int i = 0; i < a.size(); i++)
{
for (int j = 0; j < b.size(); j++)
{
int num = (a[i] - '0') * (b[j] - '0');
v[i + j] += num;//不处理进位,直接相加
}
}
int forward = 0;
int left = 0;
for (int i = 0; i < v.size(); i++)
{
left = (forward + v[i]) % 10;
forward = (forward + v[i]) / 10;
v[i] = left;
}
reverse(v.begin(), v.end());
auto it = v.begin();
while (it != v.end() && *it == 0)
it++;
if (it == v.end())
cout << "0";
else
{
while (it != v.end())
{
cout << *it;
it++;
}
}
return 0;
}4. 高精度除法
题目链接:
算法原理
我们依然模拟小学学过的除法,但是这次我们是从最高位开始除,因此我们无需倒置字符串
最后得到的字符串前面也有0,因此我们需要处理这些前导0
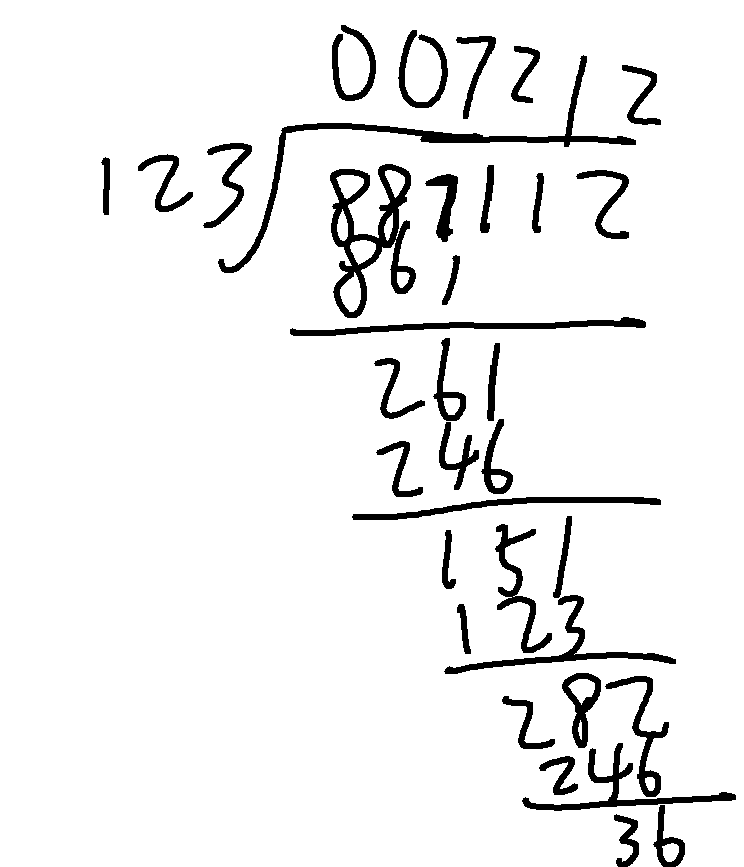
实操代码
cpp
#include <string>
#include <algorithm>
using namespace std;
int main()
{
string a;int b;cin>>a>>b;
string ret;
long long left = 0;
for(int i = 0;i<a.size();i++)
{
long long num = a[i] - '0' + left*10;
ret += (num/b) +'0';
left = num % b;
}
auto it = ret.begin();
while(it != ret.end() && *it == '0')
it++;
if(it == ret.end())
cout<<"0";
else
{
while(it != ret.end())
{
cout<<*it;
it++;
}
}
return 0;
}