文章目录
前言
本文介绍了插入排序算法的基本概念和实现过程。插入排序通过将待排序元素逐个插入已排序子序列中完成排序,具有稳定性。文章详细演示了手动排序步骤,包括元素比较和后移操作。代码实现部分提供了带哨兵和不带哨兵两种版本,哨兵版本利用数组首位减少边界判断。算法分析指出其空间复杂度为O(1),最好时间复杂度O(n)(完全有序时),平均和最坏情况下为O(n²)。插入排序适合小规模或基本有序的数据排序。
一.概念
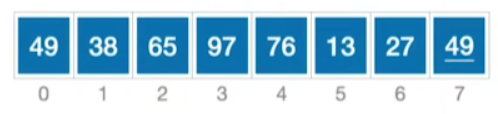
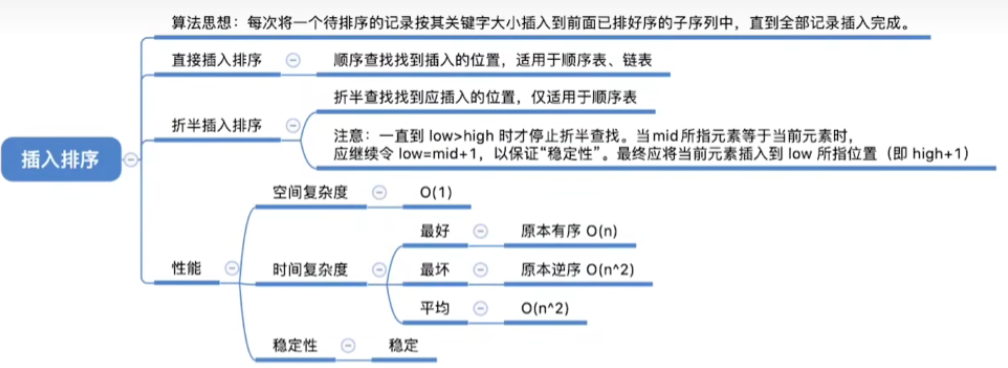
- 算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。
二.手动实现过程
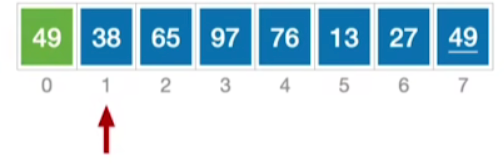
-
刚开始我们会从第二个元素开始入手,我们会认为当前处理的这个元素之前的这些部分是已经排好序的,现在我们需要把当前的这个元素38和之前已经排好序的元素依次进行对比,比当前处理的元素38更大的那些元素我们都需要将它依次后移,这里就是将49后移
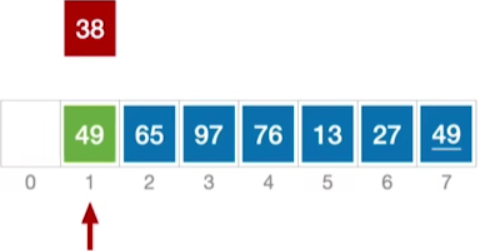
-
然后把38插入到49前面,同时指针后移处理下一个元素
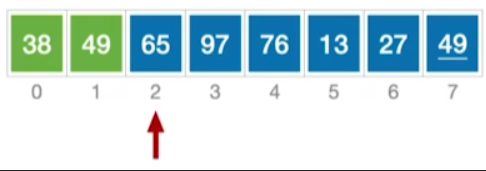
-
65要比49更大,所以如果我们是按递增排序的话,那么我们并不需要把65放到49或者38之前,因此我们把65放回来,同时指针后移
-
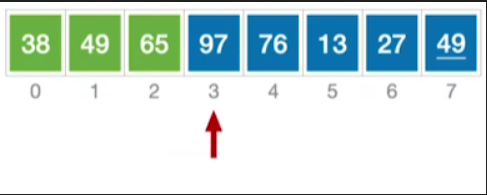
接下来也是一样,97比前面的65要大,因此97的位置不变,只需指针后移即可
-
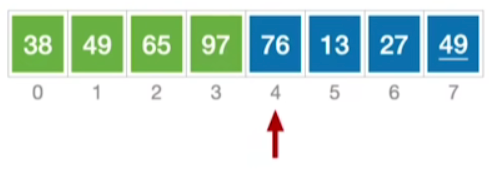
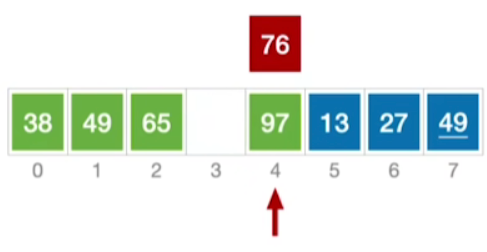
76比97小,因此97后移一位
-
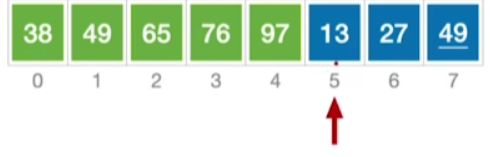
接下来看65比76小,因此插入到65的后一个单位里面
-
接下来也是一样的操作,不做多赘述,最终如下

-
可以发现原本的相同元素49的相对位置没有改变,这是由于我们只是把比它更大的这些元素全部右移,而相同元素并没有右移,因此该排序算法是稳定的
三.算法代码实现
1.不带哨兵
c
//直接插入排序
void InsertSort(int A[l,int n){
int i,j,temp;
for(i=1;i<n;i++)//将各元素插入已排好序的序列中
if(A[il<A[i-1]){//若A[i]关键字小于前驱
temp=A[i];//用temp暂存A[i]
for(j=i-1;j>=0 && A[j]>temp;--j)//检查所有前面已排好序的元素
A[j+1]=A[j];//所有大于temp的元素都向后挪位
A[j+1]=temp;//复制到插入位置
}
}- 实现思想:将当前元素与之前的元素对比,当当前元素比对比元素小时,用一个临时变量temp存储当前元素,然后循环对比它之前的所有元素,将大于它的所有元素全部后移一位,然后插入到小于它的元素的后面的位置
2.带哨兵
c
//直接插入排序(带哨兵)
void InsertSort(int A[],int n){
int i,j;
for(i=2;i<n;i++) //依次将A[2]~A[n]插入到前面已排序序列
if(A[i]<A[i-1]){ //若A[i]关键码小于其前驱,将A[i]插入有序表
A[0]=A[i]; //复制为哨兵,A[0]不存放元素
for(j=i-1;A[0]<A[j];--j)//从后往前查找待插入位置
A[j+1]=A[j]; //向后挪位
A[j+1]=A[0]; //复制到插入位置
}
}- 实现思想:空出0号地址元素当做哨兵使用 ,将当前元素与之前的元素对比,当当前元素比对比元素小时,用空出的0号地址存储当前元素,然后循环对比它之前的所有元素,将大于它的所有元素全部后移一位,然后插入到小于它的元素的后面的位置
- 与不带哨兵相比,其不用每轮循环都判断j>=0
四.算法效率
1.空间复杂度
- O(1)
2.时间复杂度
- 时间复杂度:主要来自对比关键字、移动元素若有 n 个元素,则需要 n-1 趟处理
- 最好情况:
共n-1趟处理,每一趟只需要对比关键字1次,不用移动元素
最好时间复杂度------O(n)

- 最坏情况:
第1趟:对比关键字2次,移动元素3次
第2趟:对比关键字3次,移动元素4次
...
第 i 趟:对比关键字 i+1次,移动元素 i+2 次
...
最坏时间复杂度------O(n²)

3.算法稳定性
- 稳定
五.优化------折半插入排序
1.思路
- 当前待插入元素的之前这些元素其实已经是有序且顺序存储的,因此想到折半查找
- 先用折半查找找到应该插入的位置,再移动元素
- 折半查找:
- 当 low>high 时折半查找停止,应将 [ l o w , i − 1 ] [low, i-1] [low,i−1]内的元素全部右移,并将 A [ 0 ] A[0] A[0] 复制到 low 所指位置
- 当 A [ m i d ] = = A [ 0 ] A[mid]== A[0] A[mid]==A[0]时,为了保证算法的"稳定性",应继续在 mid 所指位置右边寻找插入位置
2.具体例子
- 将i指向的元素存入地址0中,防止它被覆盖
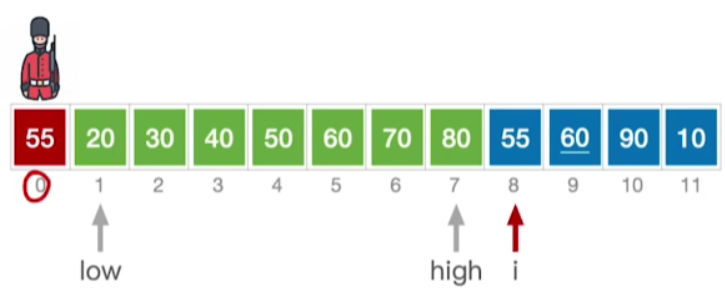
- 接下来我们会在当前这个元素前边的这个区域内,通过折半查找尝试着找到它应该插入的位置,下面就是经典的折半查找过程
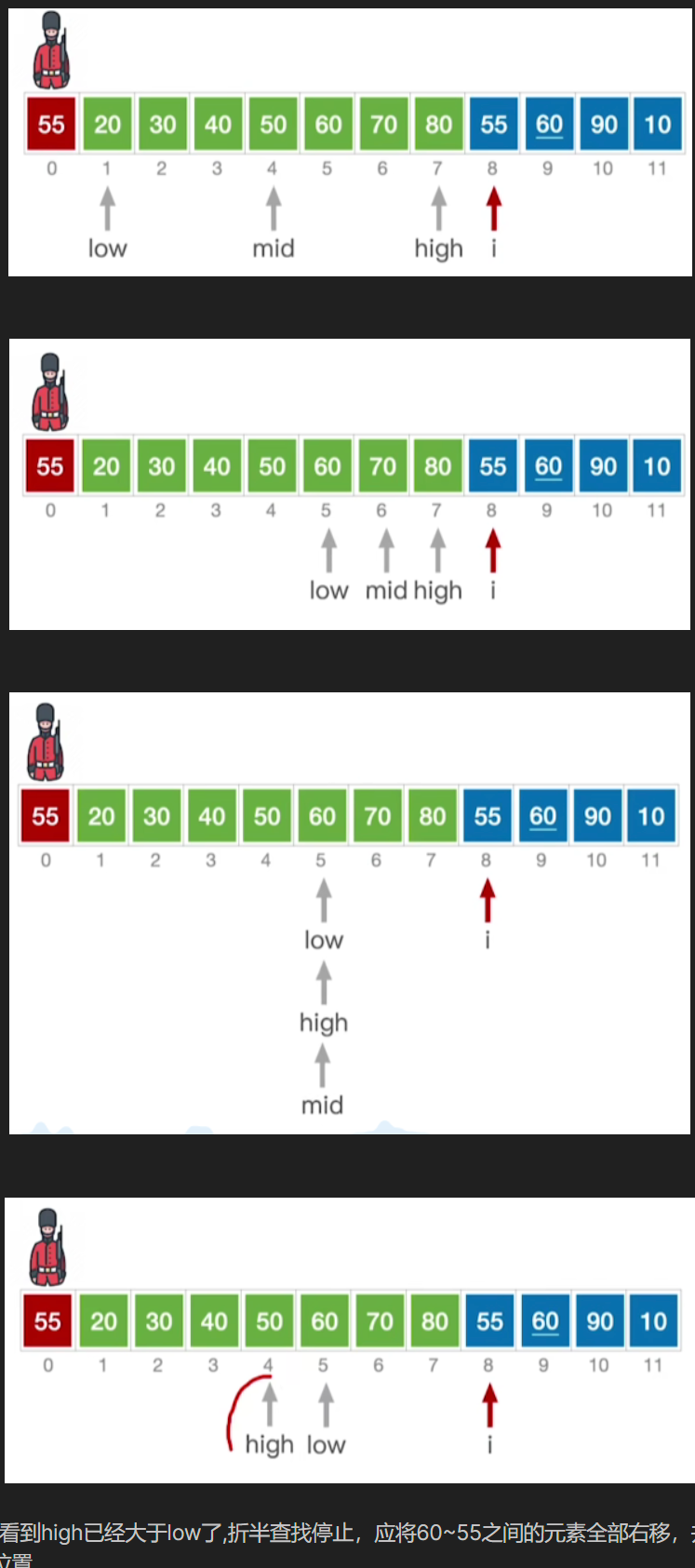
- 这一步可以看到high已经大于low了,折半查找停止,应将60~55之间的元素全部右移,并将 A [ 0 ] A[0] A[0]复制到8所指位置
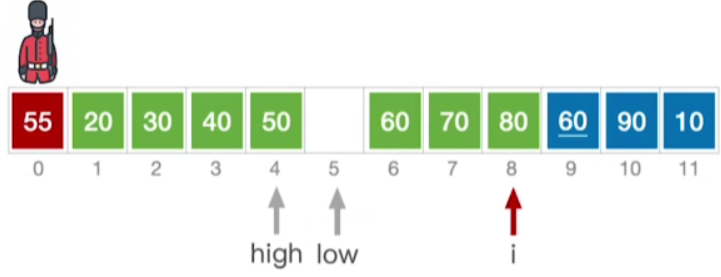
- 最后我们再把之前保存下来的这个值给它复制到low所指的位置,这样的话我们就完成了55这个元素的插入
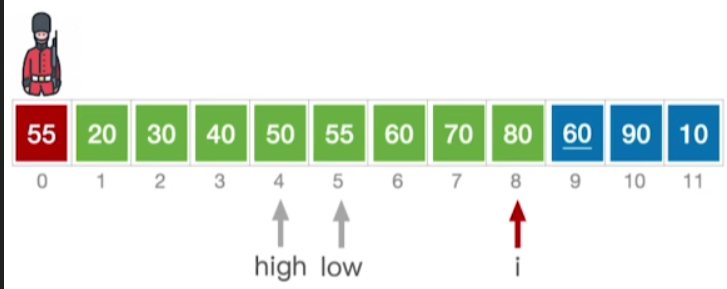
- 接下来也是一样,直到这一步
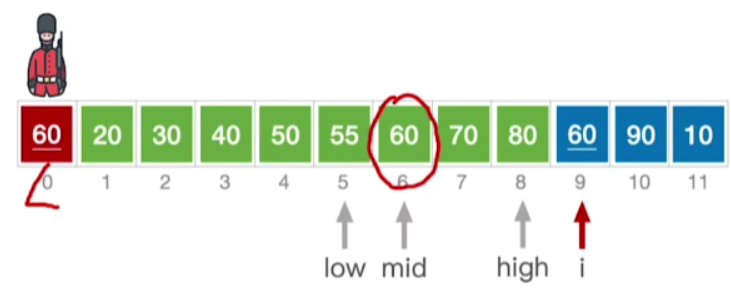
- 我们当前处理的的元素60和这儿已经有的元素60它的值是相等的,为了保证插入排序的稳定性 ,将不再使用之前的发现相同元素就停止查找的规则,而是往这个元素的右半区间内继续查找
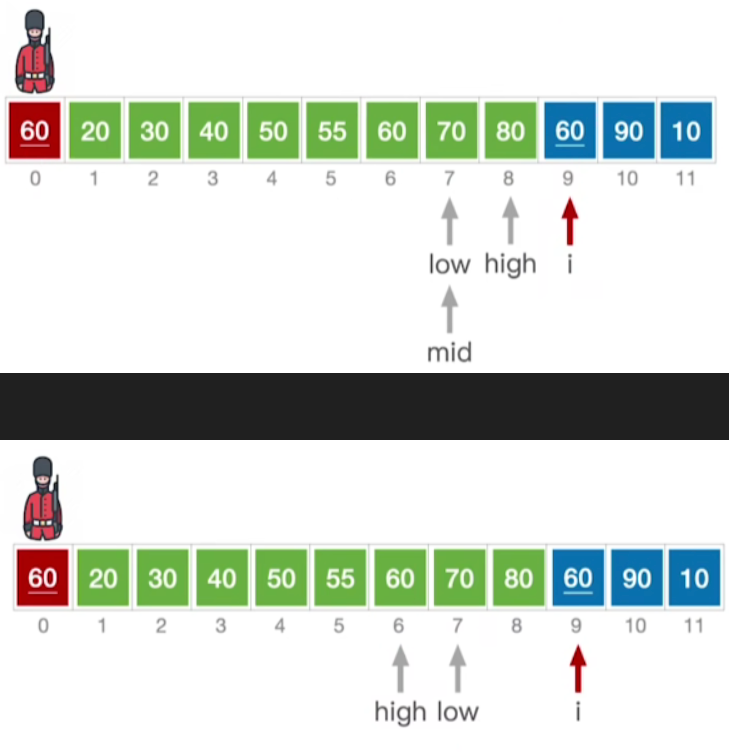
- 此时low>high,和之前处理一样了
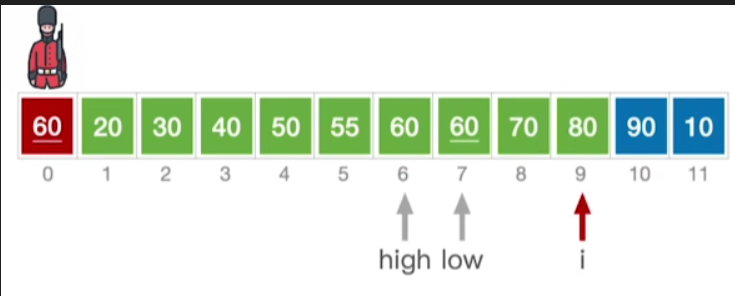
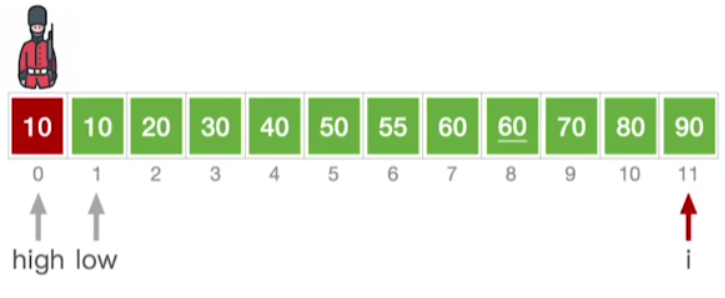
- 其他都类似,不做赘述,最终如下:
3.算法代码实现
c
//折半插入排序
void InsertSort(int A[],int n){
int i,j,low,high,mid;
for(i=2;i<=n;i++){
A[0]=A[i]; //依次将A[2]~A[n]插入前面的已排序序列
low=1;high=i-1; //将A[i]暂存到A[0]
while(low<=high){ //设置折半查找的范围
low=mid=(low+high)/2; //折半查找(默认递增有序)
if(A[mid]>A[0]) high=mid-1; //取中间点
else low=mid+1; //查找左半子表
}
for(j=i-1;j>=high+1;--j)
A[j+1]=A[j]; //统一后移元素,空出插入位置
A[high+1]=A[0]; //插入操作
}
}4.算法效率分析
- 比起"直接插入排序",比较关键字的次数减少了,但是移动元素的次数没变,
- 整体来看时间复杂度依然是O(n²)
六.对链表进行插入排序
1.算法思路
- 虚拟头节点:创建一个虚拟头节点,简化边界条件处理
- 两指针法:
lastSorted:指向已排序部分的最后一个节点curr:指向当前待排序的节点
- 插入过程:
- 如果当前节点值 ≥ 已排序部分的最后一个节点值,直接接在后面
- 否则,从链表头开始寻找插入位置,将当前节点插入到合适位置
2.算法代码实现
c
ListNode* insertionSortList2(ListNode* head) {
if (head == NULL) {
return NULL;
}
// 创建虚拟头节点
ListNode* dummy = (ListNode*)malloc(sizeof(ListNode));
dummy->next = NULL;
ListNode* curr = head;
while (curr != NULL) {
ListNode* next = curr->next; // 保存下一个节点
ListNode* prev = dummy;
// 寻找插入位置
while (prev->next != NULL && prev->next->val < curr->val) {
prev = prev->next;
}
// 插入节点
curr->next = prev->next;
prev->next = curr;
curr = next;
}
ListNode* sortedHead = dummy->next;
free(dummy); // 释放虚拟头节点
return sortedHead;
}3.算法效率分析
- 移动元素的次数变少了,但是关键字对比的次数依然是 O(n²) 数量级,
- 整体来看时间复杂度依然是 O(n²)
七.知识回顾与重要考点
结语
五更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页