Transformer 大语言模型（LLM）基石 - Transformer架构详解 - 掩码机制（Masked）原理介绍以及算法实现

锋哥原创的Transformer 大语言模型（LLM）基石视频教程：

https://www.bilibili.com/video/BV1X92pBqEhV

课程介绍

本课程主要讲解Transformer简介，Transformer架构介绍，Transformer架构详解，包括输入层，位置编码，多头注意力机制，前馈神经网络，编码器层，解码器层，输出层，以及Transformer Pytorch2内置实现，Transformer基于PyTorch2手写实现等知识。

Transformer 大语言模型（LLM）基石 - Transformer架构详解 - 掩码机制（Masked）原理介绍以及算法实现

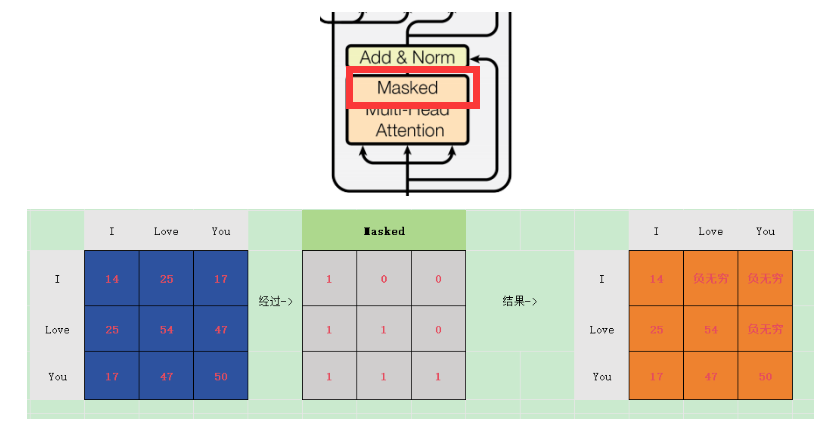
在解码器中，因为在翻译的过程中是顺序翻译的，即翻译完第 i 个单词，才可以翻译第 i+1 个单词。通过 Masked 操作可以防止泄露未来的信息。

Transformer中的掩码机制主要有两种：一种是用于处理变长序列的填充掩码（Padding Mask），另一种是用于防止未来信息泄露的序列掩码（Sequence Mask，也称为因果掩码或Look-ahead Mask）。

1. 填充掩码（Padding Mask）

在自然语言处理中，为了将多个句子组成一个批次，通常会将句子填充到相同的长度。但在计算注意力时，我们不希望模型关注这些填充的位置。因此，我们需要一个掩码来告诉模型哪些位置是填充的，从而在计算注意力时忽略这些位置。

实现方式：对于填充的位置，将其对应的注意力分数设置为一个极小的值（如-1e9），这样在softmax之后，这些位置的权重就会接近于0。

2. 序列掩码（Sequence Mask / Causal Mask）

在Transformer的解码器中，为了确保在训练时不会使用未来的信息，我们需要使用序列掩码。具体来说，对于序列中的第i个位置，我们只能关注到1到i的位置，而不能关注i+1及之后的位置。这种掩码通常用于自回归模型，如GPT。

实现方式：生成一个上三角矩阵（对角线为0），将上三角部分（即未来位置）设置为一个极小的值，这样在计算softmax时，未来位置的权重就会接近于0。

代码实现：

复制代码

import numpy as np
import torch


def create_sequence_mask(seq_len):
    """
    创建序列掩码（下三角矩阵）
    """
    mask = np.triu(np.ones((1, seq_len, seq_len), dtype=np.uint8), k=1)
    return torch.from_numpy(1 - mask)


if __name__ == '__main__':
    scores = torch.tensor([[[1, 2, 3], [4, 5, 6], [7, 8, 9]]])
    print(scores)
    mask = create_sequence_mask(3)
    scores = scores.masked_fill(mask == 0, -1e9)
    print(scores)

运行输出：

复制代码

tensor([[[1, 2, 3],
         [4, 5, 6],
         [7, 8, 9]]])
tensor([[[          1, -1000000000, -1000000000],
         [          4,           5, -1000000000],
         [          7,           8,           9]]])

np.triu() 是 NumPy 中一个非常常用的函数，用于返回矩阵的上三角部分（upper triangular part），常在矩阵运算、线性代数、神经网络权重掩码等场景中使用

函数定义：

复制代码

numpy.triu(m, k=0)

参数说明：

m：array_like 输入矩阵（可以是二维数组或更高维张量）。
k

：int，可选，默认 0

控制"对角线的偏移量"。
- k = 0 → 主对角线及其以上的元素保留；
- k > 0 → 主对角线上方第 k 条对角线及其以上的元素保留；
- k < 0 → 主对角线以下第 |k| 条对角线也会被保留下来。

具体示例：

复制代码

import numpy as np

if __name__ == '__main__':
    print('k=0\n', np.triu([
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]
    ], k=0))

    print('\nk=1\n', np.triu([
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]
    ], k=1))

    print('\nk=-1\n', np.triu([
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]
    ], k=-1))

运行输出：

复制代码

k=0
 [[1 1 1 1]
 [0 1 1 1]
 [0 0 1 1]
 [0 0 0 1]]

k=1
 [[0 1 1 1]
 [0 0 1 1]
 [0 0 0 1]
 [0 0 0 0]]

k=-1
 [[1 1 1 1]
 [1 1 1 1]
 [0 1 1 1]
 [0 0 1 1]]

NumPy 广播机制（Broadcasting）

广播（Broadcasting）是NumPy中处理不同形状数组进行算术运算的核心机制。它允许NumPy在执行逐元素操作时自动扩展较小数组的形状，使其与较大数组的形状兼容，而无需实际复制数据。

一、广播的基本规则

NumPy广播遵循三个核心规则：

规则1：如果两个数组的维度数不同，将维度较小的数组形状前面补1
规则2：对于每个维度，大小必须相等，或其中一个为1
规则3：所有维度大小都兼容后，在大小为1的维度上进行数据"复制"

二、广播示例

示例1：标量与数组的运算

复制代码

import numpy as np

# 标量广播到整个数组
a = np.array([1, 2, 3])
b = 5
result = a + b  # b被广播为[5, 5, 5]
print(result)  # 输出: [6, 7, 8]

# 相当于
# a.shape = (3,)
# b.shape = () -> 补1 -> (1,) -> 扩展为(3,)

示例2：一维数组与二维数组

复制代码

# 一维数组在列方向广播
a = np.array([[1, 2, 3],  # shape: (2, 3)
              [4, 5, 6]])
b = np.array([10, 20, 30])  # shape: (3,)

result = a + b
# b广播为: [[10, 20, 30],
#          [10, 20, 30]]
print(result)
# 输出: [[11, 22, 33],
#       [14, 25, 36]]