基于边缘图像分割算法详解与MATLAB实现

边缘图像分割是通过检测图像中灰度、颜色或纹理的突变区域（边缘）来实现目标与背景分离的技术，是计算机视觉和图像处理的核心任务之一。本文系统介绍经典边缘检测算子、边缘连接策略及分割算法

一、边缘分割基本原理

1. 边缘定义与数学模型

边缘是图像中像素灰度值发生显著变化 的位置，对应物体轮廓或不同区域的边界。数学上，边缘可通过图像的梯度描述：

一阶导数：检测灰度突变（如Sobel、Prewitt算子）
二阶导数：检测灰度极值点（如Laplacian算子），零交叉点对应边缘

二维图像f(x,y)f(x,y)f(x,y)的梯度向量为：

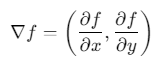
梯度幅值∣∇f∣∣∇f∣∣∇f∣反映边缘强度，方向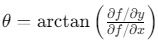

反映边缘走向。

2. 边缘分割流程

预处理：去噪（高斯滤波）、增强对比度
边缘检测：计算梯度，提取候选边缘点
边缘连接：将离散边缘点连接成连续轮廓
后处理：去除虚假边缘、细化轮廓

二、经典边缘检测算子

1. 一阶微分算子（梯度算子）

（1）Roberts算子

原理：用2x2模板计算对角线方向差分
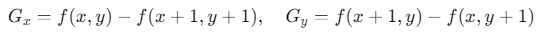
优点：计算简单，对陡峭边缘敏感
缺点：对噪声敏感，边缘定位精度低

（2）Prewitt算子

原理：用3x3模板计算水平和垂直方向差分
优点：抑制噪声能力强于Roberts
缺点：边缘较粗，定位精度一般

（3）Sobel算子

原理：加权差分模板（中心像素权重更高）
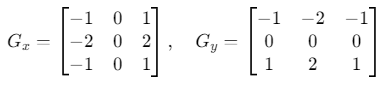
优点：边缘定位准确，抗噪性较好（最常用的一阶算子）

2. 二阶微分算子（Laplacian算子）

原理：计算图像灰度的二阶导数，边缘对应拉普拉斯响应的零交叉点
优点：各向同性，边缘定位精确
缺点：对噪声极度敏感（需先高斯滤波）

3. Canny边缘检测算子（最优边缘检测器）

Canny提出边缘检测的三个标准：低错误率、高定位精度、单边缘响应。步骤如下：

高斯滤波：去噪（标准差σ控制平滑程度）
梯度计算 ：用Sobel算子求GxG_xGx,GyG_yGy，得幅值
非极大值抑制：保留梯度方向上的局部极大值点（细化边缘）
双阈值检测：用高阈值Th（强边缘）和低阈值Tl（弱边缘，Tl≈0.4Th），连接强边缘与弱边缘

三、MATLAB实现：边缘检测与分割

1. 完整代码框架

matlab 复制代码

%% 基于边缘的图像分割算法
% 功能：实现经典边缘检测算子、Canny算子、边缘连接与分割

clear; clc; close all;

%% 1. 图像读取与预处理
img = imread('cameraman.tif');  % 经典测试图像（灰度图）
if size(img,3)==3
    img = rgb2gray(img);       % 转为灰度图
end
img = im2double(img);          % 转为double类型（0-1）

% 添加噪声（模拟实际场景）
noisy_img = imnoise(img, 'gaussian', 0, 0.01);  % 高斯噪声（方差0.01）

% 高斯滤波去噪（σ=1.5）
filtered_img = imgaussfilt(noisy_img, 1.5);


%% 2. 经典边缘检测算子实现
% Sobel算子
sobel_x = [-1 0 1; -2 0 2; -1 0 1];
sobel_y = [-1 -2 -1; 0 0 0; 1 2 1];
Gx_sobel = imfilter(filtered_img, sobel_x, 'replicate');
Gy_sobel = imfilter(filtered_img, sobel_y, 'replicate');
mag_sobel = sqrt(Gx_sobel.^2 + Gy_sobel.^2);  % 梯度幅值
edge_sobel = mag_sobel > 0.2;  % 阈值分割（经验值0.2）

% Prewitt算子
prewitt_x = [-1 0 1; -1 0 1; -1 0 1];
prewitt_y = [-1 -1 -1; 0 0 0; 1 1 1];
Gx_prewitt = imfilter(filtered_img, prewitt_x, 'replicate');
Gy_prewitt = imfilter(filtered_img, prewitt_y, 'replicate');
mag_prewitt = sqrt(Gx_prewitt.^2 + Gy_prewitt.^2);
edge_prewitt = mag_prewitt > 0.2;

% Laplacian算子（需先高斯滤波，即LoG算子）
laplacian_kernel = [0 1 0; 1 -4 1; 0 1 0];
log_img = imfilter(filtered_img, laplacian_kernel, 'replicate');
edge_log = log_img > 0;  % 零交叉点简化检测（实际需更复杂处理）


%% 3. Canny边缘检测（MATLAB内置函数+手动实现对比）
% 内置Canny函数
edge_canny_builtin = edge(filtered_img, 'Canny', [0.1 0.3]);  % 双阈值[Th, Tl]

% 手动实现Canny算子
edge_canny_manual = canny_edge_detection(filtered_img, 1.5, 0.2, 0.5);  % σ=1.5, Th=0.2, Tl=0.5


%% 4. 边缘连接与分割
% 基于边缘的区域生长（以Canny边缘为例）
segmented_img = edge_based_segmentation(filtered_img, edge_canny_manual);


%% 5. 结果可视化
visualize_results(noisy_img, filtered_img, edge_sobel, edge_prewitt, edge_log, ...
                  edge_canny_builtin, edge_canny_manual, segmented_img);


%% 6. 性能评估（边缘检测质量）
evaluate_edges(edge_canny_builtin, edge_canny_manual);  % 对比内置与手动Canny

2. 核心函数实现

（1）手动Canny边缘检测

matlab 复制代码

function edge_map = canny_edge_detection(img, sigma, Th, Tl)
    % 步骤1：高斯滤波
    img_smoothed = imgaussfilt(img, sigma);
    
    % 步骤2：计算梯度（Sobel算子）
    [Gx, Gy] = imgradientxy(img_smoothed, 'sobel');
    mag = sqrt(Gx.^2 + Gy.^2);  % 梯度幅值
    theta = atan2(Gy, Gx);      % 梯度方向（弧度）
    
    % 步骤3：非极大值抑制（细化边缘）
    [rows, cols] = size(img);
    suppressed = zeros(rows, cols);
    angle = theta * 180 / pi;  % 转为角度（-180~180）
    angle(angle < 0) = angle(angle < 0) + 180;  % 统一到0~180°
    
    for i = 2:rows-1
        for j = 2:cols-1
            q = 255; r = 255;  % 初始化邻域像素
            % 根据梯度方向判断邻域
            if (angle(i,j) >= 0 && angle(i,j) < 22.5) || (angle(i,j) >= 157.5 && angle(i,j) <= 180)
                q = mag(i, j+1); r = mag(i, j-1);  % 水平方向
            elseif angle(i,j) >= 22.5 && angle(i,j) < 67.5
                q = mag(i+1, j-1); r = mag(i-1, j+1);  % 45°方向
            elseif angle(i,j) >= 67.5 && angle(i,j) < 112.5
                q = mag(i+1, j); r = mag(i-1, j);  % 垂直方向
            elseif angle(i,j) >= 112.5 && angle(i,j) < 157.5
                q = mag(i-1, j-1); r = mag(i+1, j+1);  % 135°方向
            end
            % 保留局部极大值
            if mag(i,j) >= q && mag(i,j) >= r
                suppressed(i,j) = mag(i,j);
            end
        end
    end
    
    % 步骤4：双阈值检测与边缘连接
    strong_edges = suppressed > Th;
    weak_edges = (suppressed >= Tl) & (suppressed <= Th);
    edge_map = strong_edges;  % 初始化强边缘
    
    % 连接弱边缘（8邻域搜索强边缘）
    [rows, cols] = size(edge_map);
    for i = 2:rows-1
        for j = 2:cols-1
            if weak_edges(i,j)
                neighborhood = edge_map(i-1:i+1, j-1:j+1);
                if any(neighborhood(:))  % 邻域存在强边缘
                    edge_map(i,j) = 1;
                end
            end
        end
    end
end

（2）边缘连接与区域生长分割

matlab 复制代码

function segmented = edge_based_segmentation(img, edge_map)
    % 基于边缘的区域生长：先填充边缘内部区域
    segmented = img;  % 初始化
    mask = ~edge_map;  % 非边缘区域为待分割区域
    
    % 标记连通区域（8邻域）
    [labels, num] = bwlabel(mask, 8);
    
    % 为每个区域赋予平均灰度值（简化分割）
    for i = 1:num
        region = labels == i;
        mean_val = mean(img(region));
        segmented(region) = mean_val;
    end
end

（3）结果可视化函数

matlab 复制代码

function visualize_results(noisy, filtered, edge_sobel, edge_prewitt, edge_log, ...
                          edge_canny_builtin, edge_canny_manual, segmented)
    figure('Name', '边缘检测与分割结果', 'Position', [100, 100, 1400, 800]);
    
    % 子图1：含噪图像
    subplot(3,3,1); imshow(noisy); title('含噪图像（高斯噪声）');
    
    % 子图2：滤波后图像
    subplot(3,3,2); imshow(filtered); title('高斯滤波后图像（σ=1.5）');
    
    % 子图3：Sobel边缘
    subplot(3,3,3); imshow(edge_sobel); title('Sobel边缘检测');
    
    % 子图4：Prewitt边缘
    subplot(3,3,4); imshow(edge_prewitt); title('Prewitt边缘检测');
    
    % 子图5：LoG边缘（高斯-Laplacian）
    subplot(3,3,5); imshow(edge_log); title('LoG边缘检测');
    
    % 子图6：内置Canny边缘
    subplot(3,3,6); imshow(edge_canny_builtin); title('内置Canny边缘');
    
    % 子图7：手动Canny边缘
    subplot(3,3,7); imshow(edge_canny_manual); title('手动Canny边缘');
    
    % 子图8：边缘连接与分割结果
    subplot(3,3,8); imshow(segmented, []); title('边缘连接分割结果');
    
    % 子图9：原图与分割结果对比
    subplot(3,3,9); imshowpair(img, segmented, 'montage'); title('原图 vs 分割结果');
end

四、算法对比与性能分析

1. 经典算子对比（以cameraman图像为例）

算子	抗噪性	边缘连续性	定位精度	计算复杂度	适用场景
Roberts	差	差	低	低	无噪声、陡峭边缘
Prewitt	中	中	中	中	轻度噪声图像
Sobel	良	良	高	中	通用场景（最常用）
Laplacian	差	优	极高	低	需结合高斯滤波（LoG）
Canny	优	优	极高	高	高精度边缘检测（首选）

2. Canny算子参数影响

高斯滤波σ：σ增大→平滑增强（抗噪性↑，边缘模糊↓）；σ减小→边缘细节↑（抗噪性↓）。建议σ=0.5~2.0。
双阈值Th/Tl ：Th/Tl增大→边缘减少（漏检↑）；Th/Tl减小→边缘增多（误检↑）。推荐Th=0.2_0.5，Tl=0.10.3Th。

五、扩展：高级边缘分割算法

1. 基于活动轮廓模型（Snake算法）

原理：通过能量最小化驱动曲线（轮廓）向目标边缘演化，能量包括内部弹性力（平滑）和外部图像力（边缘吸引）。
MATLAB实现 ：activecontour函数（需二值边缘图作为输入）。

2. 基于深度学习的边缘检测

代表模型：HED（Holistically-Nested Edge Detection）、RCF（Rich Feature Hierarchies for Edge Detection）。
优势：自动学习边缘特征，适应复杂场景（如弱边缘、遮挡边缘）。

3. 多尺度边缘检测

原理：在不同尺度（σ）下检测边缘，融合多尺度结果（如小σ检测细节，大σ检测全局轮廓）。

六、应用场景

医学图像分割：CT/MRI图像中器官轮廓提取（如肿瘤边界）
自动驾驶：车道线检测、行人轮廓分割
工业检测：零件缺陷边缘定位、印刷品质量检测
遥感图像：地物边界提取（如道路、河流）

参考代码基于边缘图像分割算法 www.youwenfan.com/contentcsn/83448.html

七、总结

基于边缘的图像分割算法通过检测灰度突变实现目标分离，核心是边缘检测算子 与边缘连接策略。经典算子（Sobel、Canny）仍是工程实践的主流，而Canny算子因兼顾抗噪性与定位精度，成为高精度边缘检测的首选。实际应用中需注意：

预处理（去噪）对边缘质量至关重要；
参数（如Canny阈值）需根据具体场景调整；
复杂场景需结合区域生长、活动轮廓等后处理提升分割完整性。