《Around the Corner mmWave Imaging in Practical Environments》精读
Laura Dodds, Hailan Shanbhag, Junfeng Guan, Saurabh Gupta, and Haitham Hassanieh. 2024. Around the Corner mmWave Imaging in Practical Environments. In Proceedings of the 30th Annual International Conference on Mobile Computing and Networking (ACM MobiCom '24). Association for Computing Machinery, New York, NY, USA, 953--967.
(文内默认 LOS =视距、NLOS =非视距;mmWave =毫米波;SAR =合成孔径雷达;specular=镜面反射。)

0. 论文的中心命题与"难点来源"
论文提出并实现 RFlect :在不改造环境(不贴泡沫/不装金属镜)且反射体不再被简化为"唯一平面"的现实条件下,利用 LOS 区域内的真实反射体 (墙面、柱体、凹面、复合多面等)生成 绕角的高分辨率 NLOS mmWave 图像。图 1 在第一页用"拐角 + 柱体 + 人体"的示意强调:雷达与目标处于彼此 NLOS,但回波可沿"雷达→反射体→目标→反射体→雷达"的路径返回,从而让目标被"成像"。
难点并不止"能量能否回来",而是"相位能否对齐"。在 mmWave 成像里,高分辨率依赖跨天线、跨频率的相干叠加;一旦反射几何建模出现厘米级误差(尤其柱体半径/中心偏差),相位补偿就会错位,导致重建图像畸变或出现幽灵目标(ghost)。论文在引言直接点出:凸面反射会把信号在角域里强烈"扩散",使角分辨率在某些场景可恶化到平面反射的 22 倍;而这种分辨率损失与几何误差敏感性一起,构成"真实环境绕角高分辨率成像"此前难以落地的根本原因。
1. LOS mmWave 成像"底座":匹配滤波式 (1) 与角分辨率式 (2)
论文先回到 LOS 成像(不经反射)作为基线,并给出最直接的 matched filter(或称 backprojection)热图构造。对空间中任意体素 v=(x,y,z)v=(x,y,z)v=(x,y,z),反射功率被写成对天线索引 iii 与频率采样索引 nnn 的相干求和:
P(v)=∣∑i=1A∑n=1Ns(n,i) ej2πc d(v,i) (f+kn)∣.(1) P(v)=\left|\sum_{i=1}^{A}\sum_{n=1}^{N}s(n,i)\,e^{j\frac{2\pi}{c}\,d(v,i)\,(f+kn)}\right|. \tag{1} P(v)= i=1∑An=1∑Ns(n,i)ejc2πd(v,i)(f+kn) .(1)
符号含义在论文中是成像领域约定俗成的:s(n,i)s(n,i)s(n,i) 为第 iii 个接收通道在第 nnn 个采样频点的复基带回波;fff 是 chirp 起始频率,kkk 是频率步进/斜率离散化系数;d(v,i)d(v,i)d(v,i) 是假设散射点位于 vvv 时,从第 iii 个天线到该点的往返路径长度;ccc 为光速。式 (1) 的核心是:如果真实散射点正是 vvv,那么 s(n,i)s(n,i)s(n,i) 的相位随频率变化与 d(v,i)d(v,i)d(v,i) 一致,乘上指数项后会被"解相位",从而在所有 (n,i)(n,i)(n,i) 上相干累加并形成峰值;若 vvv 不是真实散射点,则相位无法同时对齐,求和后互相抵消。
角分辨率方面,论文采用经典近似:
δθ≈λDxcosθ,δϕ≈λDzcosϕ.(2) \delta\theta \approx \frac{\lambda}{D_x\cos\theta},\qquad \delta\phi \approx \frac{\lambda}{D_z\cos\phi}. \tag{2} δθ≈Dxcosθλ,δϕ≈Dzcosϕλ.(2)
λ\lambdaλ 为载频波长,Dx,DzD_x,D_zDx,Dz 为孔径在水平/垂直方向的长度,θ,ϕ\theta,\phiθ,ϕ 为体素相对孔径中心的方位/俯仰角。它将"孔径越长越能分辨更小角度差、偏轴越大分辨越差"的阵列基本事实压缩成一行表达。论文后续的理论分析(分辨率与覆盖)几乎都在把式 (2) 的 LOS 分辨率通过"反射几何变换"映射到 NLOS 域。
2. RFlect 的三段式闭环:分类 → 精映射 → 反射成像
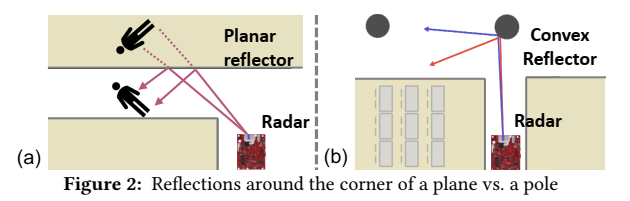
图 2 用"平面 vs 柱体"的射线示意提前给出系统逻辑:平面反射更像镜子,不会显著改变角谱结构;柱体(凸面)会改变射线束的发散/收敛关系,从而改变分辨率与覆盖。RFlect 的整体流程在算法 1 中被写成三段:
- 先用式 (1) 生成 LOS SAR 图 并阈值分割出 LOS 反射体点集;依据点集数量与线/弧拟合残差将反射体粗分为 planar / convex / concave。
- 对 planar 用线拟合得到参数;对 convex/concave 用"对几何参数做 matched filter"的方法精确求 (xc,yc,r)(x_c,y_c,r)(xc,yc,r)(圆心与半径)。
- 再用对应反射模型把 NLOS 的路径长度写对,从而在 NLOS 域也能做相干叠加成像。
论文把"分类"放在工程可行性层面:真实环境可能同时存在墙、门、柜体、柱、显示器等,若不先把主导反射几何搞清楚,后续相干叠加会把不同路径硬加在一起,必然出现 ghost。
3. 绕角成像建模:平面镜像为何足够、曲面为何不够
3.1 单平面:镜像法与"看似简单但条件很强"
在单平面反射中,论文采用最直观的镜像解释:若只做 LOS 匹配滤波,目标会被重建到"墙后"成为镜像目标;已知反射平面后,把该镜像再反射回真实空间即可得到 NLOS 目标位置与形状。其关键隐含条件是:平面反射使得"反射路径"等价于"到镜像点的直达路径",因此跨天线相位仍能一致对齐,式 (1) 的相干累加仍成立。
3.2 凸/凹曲面:失败不是"能量弱",而是"相位错位"
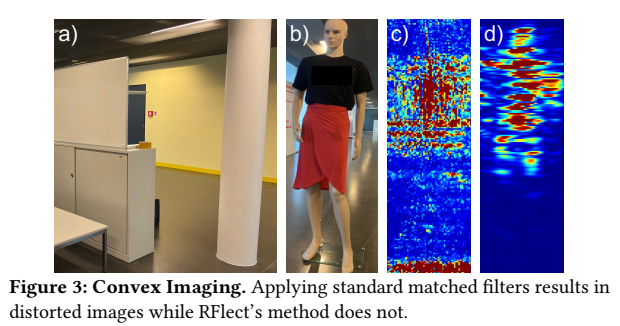
图 3 给出一个非常典型的现象:对凸面柱体,如果沿用平面镜像那套(即继续使用式 (1) 里的直达距离模型),图像会发生系统性扭曲;而采用 RFlect 的曲面反射建模后,形状能显著恢复。
作者将原因归结为:曲面不再是"全局一个法向量",镜面反射点随入射/出射方向改变。对同一体素 vvv,不同天线位置 iii 的主导反射点一般不同;若仍用一个"错误的路径长度"去补偿相位,跨天线叠加不再相干,能量被摊散成畸变与噪声结构。
为此论文把成像公式改写成"按镜面路径"匹配滤波:
Pc(v)=∣∑i=1A∑n=1Ns(n,i) ej2πc d(v,pr,i) (f+kn)∣.(3) P_c(v)=\left|\sum_{i=1}^{A}\sum_{n=1}^{N}s(n,i)\,e^{j\frac{2\pi}{c}\,d(v,p_r,i)\,(f+kn)}\right|. \tag{3} Pc(v)= i=1∑An=1∑Ns(n,i)ejc2πd(v,pr,i)(f+kn) .(3)
其中 pr=pr(v,i)p_r=p_r(v,i)pr=pr(v,i) 是"使得天线 iii 与体素 vvv 之间满足镜面反射定律"的曲面点;路径长度以一次反射的折线写成:
d(v,pr,i)=2(∥v−pr∥+∥pr−pi∥). d(v,p_r,i)=2\big(\|v-p_r\|+\|p_r-p_i\|\big). d(v,pr,i)=2(∥v−pr∥+∥pr−pi∥).
式 (3) 的结构与式 (1) 一致,差异集中在 距离模型 :LOS 是 d(v,i)d(v,i)d(v,i),曲面 NLOS 是 d(v,pr,i)d(v,p_r,i)d(v,pr,i)。换言之,RFlect 把绕角曲面成像的核心计算压缩为一个几何问题:对每个 (v,i)(v,i)(v,i),求镜面点 pr(v,i)p_r(v,i)pr(v,i)。
3.3 多反射体:ghost 的来源不是"噪声",而是"多条物理可行路径被混合"

图 4 展示两块分段平面(墙面 + 门板)时的成像现象:只按其中一个平面建模,另一平面的反射会被错误聚焦,形成 ghost;同时还存在"去程/回程走不同面"的组合路径,使得理论上会出现四种组合,实际会形成多个幽灵副本。
论文将"两次反射"写为依次经过 pr1,pr2p_{r1},p_{r2}pr1,pr2 的折线路径长度:
d(v,pr1,pr2)=2(∥pi−pr1∥+∥pr1−pr2∥+∥pr2−v∥), d(v,p_{r1},p_{r2}) =2\big(\|p_i-p_{r1}\|+\|p_{r1}-p_{r2}\|+\|p_{r2}-v\|\big), d(v,pr1,pr2)=2(∥pi−pr1∥+∥pr1−pr2∥+∥pr2−v∥),
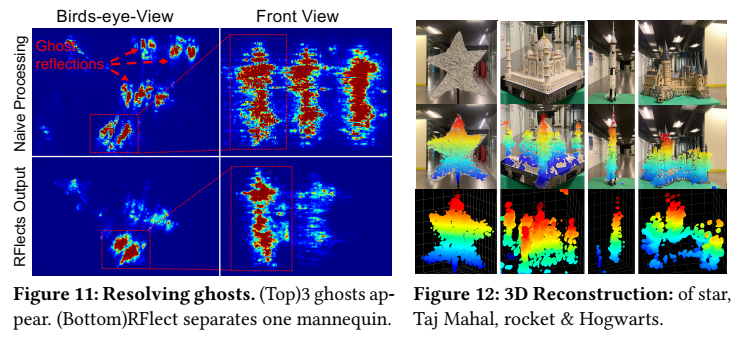
然后对每种候选路径都以式 (3) 的形式做相干聚焦,并利用"只有正确路径能在同一空间位置上形成强峰"的机制把 ghost 压下去。图 11(后文评估页)用"3 个 ghost → 1 个真实人形"的结果证明:ghost 本质上来自路径未分离的相干叠加错误,而不是随机噪声。
4. 理论部分的主线:把 LOS 分辨率"反射过去",得到 NLOS 分辨率
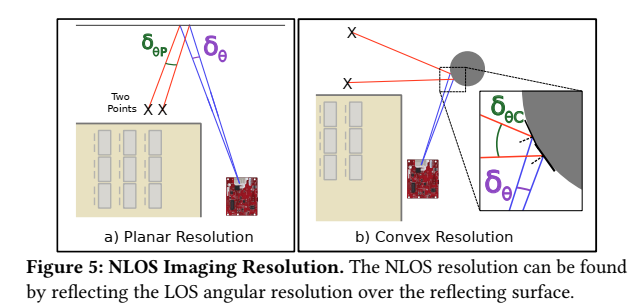
第 6 节的建模思路非常统一:孔径的 LOS 角分辨率已由式 (2) 给出,可视化成图 5 的两条"蓝色边界射线";要得到 NLOS 分辨率,就把这两条射线按反射几何映射(红色射线),再取红色射线之间的夹角作为 NLOS 可分辨的最小角间隔。
4.1 平面反射下分辨率不变:式 (8) 的几何含义
论文在 2D 平面(只讨论水平分辨率)里,把雷达放在原点 (0,0)(0,0)(0,0)。对体素 v=(x,y)v=(x,y)v=(x,y),先求与平面镜面反射对应的反射点 (xr,yr)(x_r,y_r)(xr,yr),并写出反射信号在雷达端的到达角:
θ=arctan(yrxr).(4) \theta=\arctan\left(\frac{y_r}{x_r}\right). \tag{4} θ=arctan(xryr).(4)
平面用单位法向量 n=(nx,ny)\mathbf n=(n_x,n_y)n=(nx,ny) 与常数 DDD 表示为 nxx+nyy+D=0n_x x+n_y y+D=0nxx+nyy+D=0。论文在式 (4) 上方给出了 (xr,yr)(x_r,y_r)(xr,yr) 的解析表达(其本质是"镜像点连线与平面交点",附录会补全推导)。
接下来用式 (2) 在角度 θ\thetaθ 处取 LOS 分辨率 δθ\delta\thetaδθ,并构造两条边界射线:
r1=[cos(θ−δθ2)sin(θ−δθ2)],r2=[cos(θ+δθ2)sin(θ+δθ2)].(5) \mathbf r_1= \begin{bmatrix} \cos\left(\theta-\frac{\delta\theta}{2}\right)\\ \sin\left(\theta-\frac{\delta\theta}{2}\right) \end{bmatrix},\quad \mathbf r_2= \begin{bmatrix} \cos\left(\theta+\frac{\delta\theta}{2}\right)\\ \sin\left(\theta+\frac{\delta\theta}{2}\right) \end{bmatrix}. \tag{5} r1=[cos(θ−2δθ)sin(θ−2δθ)],r2=[cos(θ+2δθ)sin(θ+2δθ)].(5)
将两条射线按平面法向量做镜面反射:
r1′=r1−2(r1⋅n)n,r2′=r2−2(r2⋅n)n.(6) \mathbf r_1'=\mathbf r_1-2(\mathbf r_1\cdot \mathbf n)\mathbf n,\qquad \mathbf r_2'=\mathbf r_2-2(\mathbf r_2\cdot \mathbf n)\mathbf n. \tag{6} r1′=r1−2(r1⋅n)n,r2′=r2−2(r2⋅n)n.(6)
平面反射后的角分辨率定义为两反射射线夹角:
δθP=arccos(r1′⋅r2′∥r1′∥ ∥r2′∥).(7) \delta\theta_P=\arccos\left(\frac{\mathbf r_1'\cdot \mathbf r_2'}{\|\mathbf r_1'\|\,\|\mathbf r_2'\|}\right). \tag{7} δθP=arccos(∥r1′∥∥r2′∥r1′⋅r2′).(7)
并给出结论:
δθP=arccos(cos(δθ))=δθ.(8) \delta\theta_P=\arccos(\cos(\delta\theta))=\delta\theta. \tag{8} δθP=arccos(cos(δθ))=δθ.(8)
这一步在原文里是"代入并化简",几何意义是:关于平面的镜像反射是一个正交变换(保持内积),因此射线夹角保持不变;平面既不汇聚也不发散射线束,所以 NLOS 水平角分辨率与 LOS 相同。
4.2 凸/凹曲面:分辨率被曲率"改写",式 (14) 给出通用计算
对凸/凹曲面(2D 截面近似为圆),论文同样先找体素 v=(x,y)v=(x,y)v=(x,y) 在曲面反射后的到达角:
θc=arctan(yr,cxr,c),(9) \theta_c=\arctan\left(\frac{y_{r,c}}{x_{r,c}}\right), \tag{9} θc=arctan(xr,cyr,c),(9)
其中 (xr,c,yr,c)(x_{r,c},y_{r,c})(xr,c,yr,c) 是体素与雷达之间的镜面反射点(原文引用 Alhazen/Ptolemy--Alhazen 问题的求解路径,附录 A 也提供代数解框架)。
然后构造两条 LOS 边界射线:
r1,c=[cos(θc−δθ2)sin(θc−δθ2)],r2,c=[cos(θc+δθ2)sin(θc+δθ2)].(10) \mathbf r_{1,c}= \begin{bmatrix} \cos\left(\theta_c-\frac{\delta\theta}{2}\right)\\ \sin\left(\theta_c-\frac{\delta\theta}{2}\right) \end{bmatrix},\quad \mathbf r_{2,c}= \begin{bmatrix} \cos\left(\theta_c+\frac{\delta\theta}{2}\right)\\ \sin\left(\theta_c+\frac{\delta\theta}{2}\right) \end{bmatrix}. \tag{10} r1,c=[cos(θc−2δθ)sin(θc−2δθ)],r2,c=[cos(θc+2δθ)sin(θc+2δθ)].(10)
接着计算两条射线与圆(圆心 c\mathbf cc,半径 rrr)的交点。论文把这一步写成判别式形式:
b1=−2 c⋅r1,c,b2=−2 c⋅r2,c, b_1=-2\,\mathbf c\cdot \mathbf r_{1,c},\quad b_2=-2\,\mathbf c\cdot \mathbf r_{2,c}, b1=−2c⋅r1,c,b2=−2c⋅r2,c,
d1=b12−4(∥c∥2−r2),d2=b22−4(∥c∥2−r2), d_1=b_1^2-4(\|\mathbf c\|^2-r^2),\quad d_2=b_2^2-4(\|\mathbf c\|^2-r^2), d1=b12−4(∥c∥2−r2),d2=b22−4(∥c∥2−r2),
pi,1=−b1±d12 r1,c,pi,2=−b2±d22 r2,c.(11) \mathbf p_{i,1}=\frac{-b_1\pm\sqrt{d_1}}{2}\,\mathbf r_{1,c},\qquad \mathbf p_{i,2}=\frac{-b_2\pm\sqrt{d_2}}{2}\,\mathbf r_{2,c}. \tag{11} pi,1=2−b1±d1 r1,c,pi,2=2−b2±d2 r2,c.(11)
符号 ±\pm± 的取法与凸/凹有关:凸面取"−-−"分支,凹面取"+++"分支;原文注释也指出若 d1<0d_1<0d1<0 或 d2<0d_2<0d2<0 则无交点(对应射线未击中曲面)。
交点处法向量取径向归一化:
n1=pi,1−c∥pi,1−c∥,n2=pi,2−c∥pi,2−c∥.(12) \mathbf n_1=\frac{\mathbf p_{i,1}-\mathbf c}{\|\mathbf p_{i,1}-\mathbf c\|},\qquad \mathbf n_2=\frac{\mathbf p_{i,2}-\mathbf c}{\|\mathbf p_{i,2}-\mathbf c\|}. \tag{12} n1=∥pi,1−c∥pi,1−c,n2=∥pi,2−c∥pi,2−c.(12)
反射射线由镜面反射公式得到:
r1,c′=r1,c−2(r1,c⋅n1)n1,r2,c′=r2,c−2(r2,c⋅n2)n2.(13) \mathbf r_{1,c}'=\mathbf r_{1,c}-2(\mathbf r_{1,c}\cdot\mathbf n_1)\mathbf n_1,\qquad \mathbf r_{2,c}'=\mathbf r_{2,c}-2(\mathbf r_{2,c}\cdot\mathbf n_2)\mathbf n_2. \tag{13} r1,c′=r1,c−2(r1,c⋅n1)n1,r2,c′=r2,c−2(r2,c⋅n2)n2.(13)
最终曲面反射下的理论分辨率定义为夹角:
δθC=arccos(r1,c′⋅r2,c′∥r1,c′∥ ∥r2,c′∥).(14) \delta\theta_C=\arccos\left(\frac{\mathbf r_{1,c}'\cdot \mathbf r_{2,c}'}{\|\mathbf r_{1,c}'\|\,\|\mathbf r_{2,c}'\|}\right). \tag{14} δθC=arccos(∥r1,c′∥∥r2,c′∥r1,c′⋅r2,c′).(14)
与平面情况最大的差异并不在公式形式,而在 n1,n2\mathbf n_1,\mathbf n_2n1,n2 随交点变化:平面 n\mathbf nn 恒定导致"整体镜像"、夹角保持;圆面 n\mathbf nn 随入射点改变导致"角间隔被曲率重新映射",从而可出现凸面分辨率变差、凹面在特定几何下可能改善的现象(论文在微基准里也用仿真曲线展示了这种距离/角度依赖性)。
5. 覆盖范围理论:反射体决定"能看到多宽"
作者将覆盖(coverage)理解为:把不同 AoA 的射线"扫过"反射面后,反射射线能覆盖到 NLOS 空间的哪些区域。对 planar/convex/concave 三类反射体,覆盖在每个维度上都可由两条边界射线限定,于是只需处理"边界怎么反射"。
5.1 平面覆盖:由平面左右边界反射给出
设 bL,bR\mathbf b_L,\mathbf b_RbL,bR 为指向平面左/右边界的射线方向(论文在 2D 推导里把它们视作边界向量),则反射边界射线为:
rL=bL−2(bL⋅n)n,rR=bR−2(bR⋅n)n,(15) \mathbf r_L=\mathbf b_L-2(\mathbf b_L\cdot \mathbf n)\mathbf n,\qquad \mathbf r_R=\mathbf b_R-2(\mathbf b_R\cdot \mathbf n)\mathbf n, \tag{15} rL=bL−2(bL⋅n)n,rR=bR−2(bR⋅n)n,(15)
覆盖角为:
ΘP=arccos(rL⋅rR∥rL∥ ∥rR∥).(16) \Theta_P=\arccos\left(\frac{\mathbf r_L\cdot \mathbf r_R}{\|\mathbf r_L\|\,\|\mathbf r_R\|}\right). \tag{16} ΘP=arccos(∥rL∥∥rR∥rL⋅rR).(16)
5.2 凸面覆盖:完整圆由两条切线决定
凸面(柱体截面视作完整圆)时,论文用"从孔径中心作圆的两条切线"界定覆盖边界:反射射线必在两条切线外侧。设切线斜率为 m1,m2m_1,m_2m1,m2,两切线夹角 θt\theta_tθt 写成:
θt=arctan∣m1−m21+m1m2∣.(17) \theta_t=\arctan\left|\frac{m_1-m_2}{1+m_1m_2}\right|. \tag{17} θt=arctan 1+m1m2m1−m2 .(17)
最终覆盖角:
ΘC=2π−θt.(18) \Theta_C=2\pi-\theta_t. \tag{18} ΘC=2π−θt.(18)
其直观含义是:圆在孔径原点"遮住"了一个角域(两切线之间),其余角域都可经反射到达;因此用 2π−θt2\pi-\theta_t2π−θt 表示可覆盖的角宽。
5.3 凹面覆盖:由弧段左右端点反射给出
凹面往往不是完整圆(例如曲面显示器只占圆的一段),因此覆盖边界由弧段左右端点决定。论文记左右端点方向为 bL,c,bR,c\mathbf b_{L,c},\mathbf b_{R,c}bL,c,bR,c,端点法向量为 nL,nR\mathbf n_L,\mathbf n_RnL,nR,则反射边界射线:
rL,c=bL,c−2(bL,c⋅nL)nL,rR,c=bR,c−2(bR,c⋅nR)nR,(19) \mathbf r_{L,c}=\mathbf b_{L,c}-2(\mathbf b_{L,c}\cdot\mathbf n_L)\mathbf n_L,\qquad \mathbf r_{R,c}=\mathbf b_{R,c}-2(\mathbf b_{R,c}\cdot\mathbf n_R)\mathbf n_R, \tag{19} rL,c=bL,c−2(bL,c⋅nL)nL,rR,c=bR,c−2(bR,c⋅nR)nR,(19)
覆盖角:
ΘV=arccos(rL,c⋅rR,c∥rL,c∥ ∥rR,c∥).(20) \Theta_V=\arccos\left(\frac{\mathbf r_{L,c}\cdot \mathbf r_{R,c}}{\|\mathbf r_{L,c}\|\,\|\mathbf r_{R,c}\|}\right). \tag{20} ΘV=arccos(∥rL,c∥∥rR,c∥rL,c⋅rR,c).(20)

图 6 把理论与工程连接起来:平面点云密、可直接线拟合;凸/凹面因镜面性只在少量点"亮",用普通拟合会偏,必须用更强的参数化相位匹配来求几何,否则成像会被厘米级误差摧毁。
6. 反射体精确映射:把"几何参数"当作匹配滤波的搜索维度
第 7 节给出一个与直觉相反但在相干处理上很自然的策略:对非平面反射体,先做"把反射体成像出来再拟合"并不稳,因为镜面反射使点云稀疏且偏置;更有效的是直接对反射体的低维参数做 matched filter,让"正确参数"在相位上产生最大相干增益。
对柱体(圆)用参数 (xc,yc,r)(x_c,y_c,r)(xc,yc,r) 描述。对任一候选参数,先对每个天线 pa,ip_{a,i}pa,i 求"从该天线发出并镜面反射回到自身"的镜面点 prp_rpr,再用该往返距离做相位补偿并跨 (n,i)(n,i)(n,i) 相干累加,得到模型得分:
S(xc,yc,r)=∣∑i=1A∑n=1Ns(n,i) ej2πc d(pa,i,pr) (f+kn)∣.(21) S(x_c,y_c,r)=\left|\sum_{i=1}^{A}\sum_{n=1}^{N} s(n,i)\, e^{j\frac{2\pi}{c}\,d(p_{a,i},p_r)\,(f+kn)}\right|. \tag{21} S(xc,yc,r)= i=1∑An=1∑Ns(n,i)ejc2πd(pa,i,pr)(f+kn) .(21)
最后在由 LOS 粗定位得到的参数集合 BBB 内取最大者:
(x^c,y^c,r^)=max(xc,yc,r)∈BS(xc,yc,r).(22) (\hat x_c,\hat y_c,\hat r)=\max_{(x_c,y_c,r)\in B} S(x_c,y_c,r). \tag{22} (x^c,y^c,r^)=(xc,yc,r)∈BmaxS(xc,yc,r).(22)
其"高精度"来自相干性:正确几何让每个通道的相位补偿一致,∣∑ejϕ∣|\sum e^{j\phi}|∣∑ejϕ∣ 接近线性增长;错误几何使相位散开,叠加被抵消。图 13(后文)展示了这种相位敏感性的负面侧:即使只在中心或半径上加 1--5 cm 误差,NLOS 图像也会立刻明显扭曲。

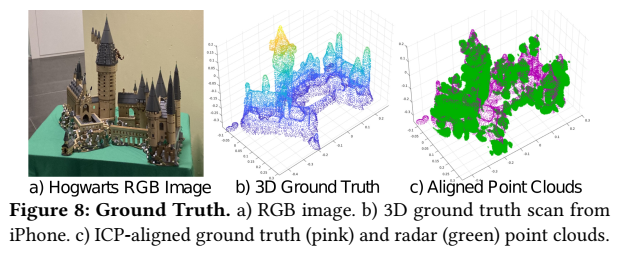
图 7 给出评测反射体(3 种平面、3 根混凝土柱、一个塑料凹面、一个木+混凝土复合面);图 8 展示真值获取:用 iPhone 12 Pro LiDAR + Polycam 360° 扫描得到点云,并用 ICP 与雷达点云对齐。
7. 评估:从"能看见"到"形状可用",再到"误差敏感性"被定量化
7.1 2D 热图质化结果:平面反射可接近同距离 LOS;凸/凹/复合依赖建模与映射
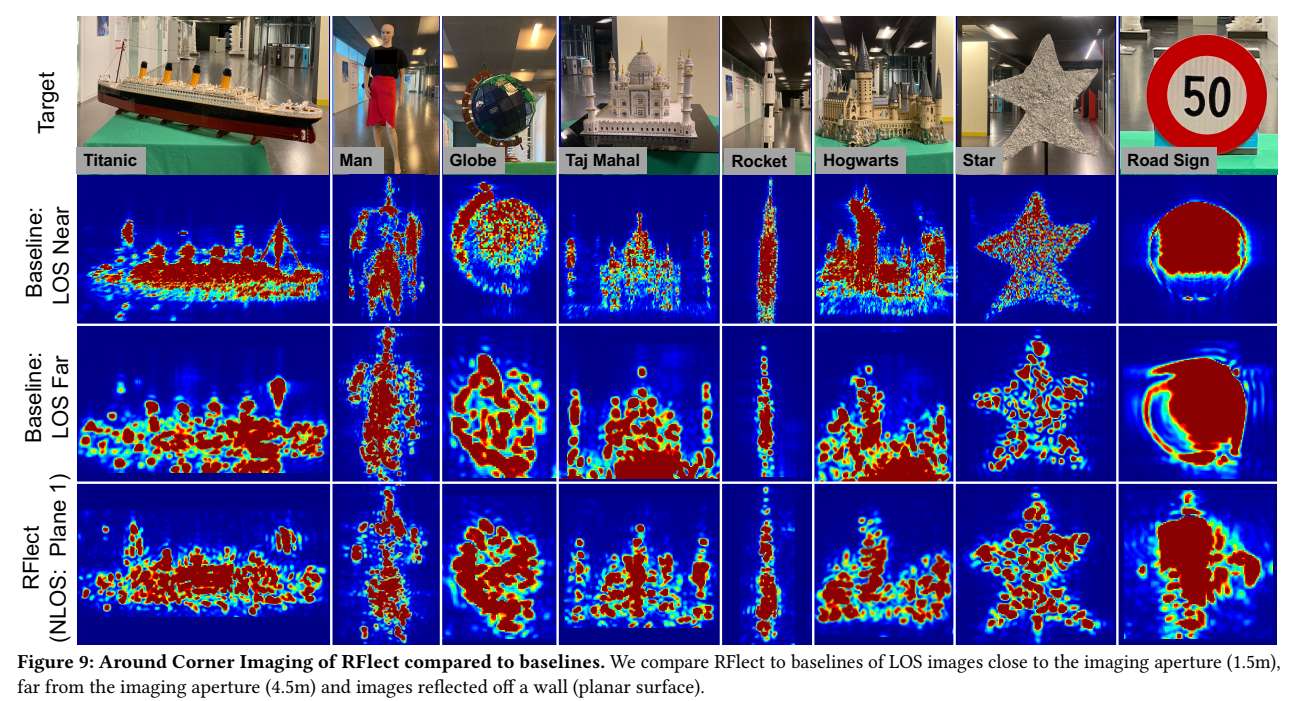
图 9 把 RFlect(平面反射绕角)与两种 LOS 基线对齐比较:LOS Near(约 1.5 m)、LOS Far(约 4.5 m)、以及"雷达到墙 3.5 m + 墙到目标 1.5 m"的 NLOS,总路径接近 LOS Far。图中每个目标(Titanic、Mannequin、Globe、Taj Mahal、Rocket、Hogwarts、Star、Road Sign)给出 RGB 与热图。论文强调两点:其一,平面反射下能重建结构细节(如 Star 五个角、Taj Mahal 两根细柱);其二,热图分辨率与 LOS Far 接近,这与理论中"平面不改变角分辨率"相一致。
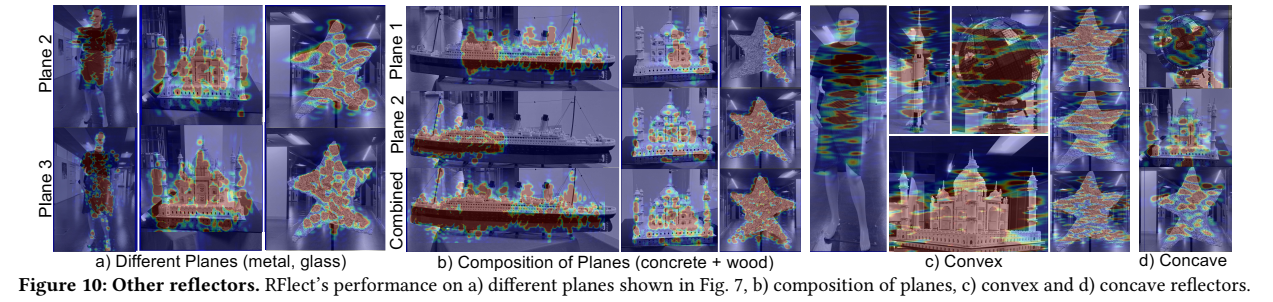
图 10 把反射体扩展到不同材质平面、复合平面、凸面柱体与凹面显示器;图 11 聚焦 ghost 的消解;图 12 展示 3D 点云重建(把热图阈值化成点云,并按高度着色);图 13 专门做"映射误差注入"实验:对柱体中心位置或半径分别加入 1/3/5 cm(半径一组还包括 9.5 cm),可见图像迅速畸变,直接佐证第 7 节映射算法的必要性。
7.2 量化指标:Chamfer Distance 与 3D F-Score
论文将阈值化后的雷达点云 PRP_RPR 与真值点云 PGP_GPG 做 ICP 对齐后,计算双向 Chamfer 距离:
CD(PR,PG)=12NR∑i=1NRd(xi,PG)+12NG∑j=1NGd(xj,PR),(23) CD(P_R,P_G)= \frac{1}{2N_R}\sum_{i=1}^{N_R} d(x_i,P_G)+ \frac{1}{2N_G}\sum_{j=1}^{N_G} d(x_j,P_R), \tag{23} CD(PR,PG)=2NR1i=1∑NRd(xi,PG)+2NG1j=1∑NGd(xj,PR),(23)
其中 d(x,P)=minx′∈P∥x−x′∥d(x,P)=\min_{x'\in P}\|x-x'\|d(x,P)=minx′∈P∥x−x′∥。F-Score 由阈值 τ=0.05\tau=0.05τ=0.05 m 下的 precision/recall 组成(论文也说明会在多阈值上取最佳以避免阈值选择偏置)。
7.3 表 1 与表 2:平面反射接近 LOS;凸面最难;凹面与复合在该设置下表现更稳定
为避免把"图像"重新解释成另一套指标,论文把表格作为最终定量结论载体。根据表 1(LOS Far vs Planar)与表 2(Complex Surfaces):
表 1:LOS Far 与平面反射(Plane 1)对比
| 目标 | LOS Far CD | LOS Far FS | Planar CD | Planar FS |
|---|---|---|---|---|
| Titanic | 0.02 | 0.90 | 0.03 | 0.87 |
| Mannequin | 0.04 | 0.67 | 0.04 | 0.70 |
| Globe | 0.01 | 0.97 | 0.02 | 0.96 |
| Taj Mahal | 0.03 | 0.88 | 0.02 | 0.90 |
| Rocket | 0.01 | 1.00 | 0.01 | 0.99 |
| Hogwarts | 0.01 | 0.97 | 0.01 | 0.97 |
| Star | 0.01 | 0.99 | 0.01 | 0.99 |
| Road Sign | 0.01 | 0.99 | 0.04 | 0.69 |
表 1 下半部分还给出 Plane 2 与 Plane 3 的部分对象结果(Mannequin / Globe / Star),总体与 Plane 1 的趋势一致,但 Road Sign 在 planar 下明显变差,论文将其解释为目标自身高镜面性导致当其姿态不垂直入射时更难成像。
表 2:复杂反射体
| 类别 | 目标 | CD | FS |
|---|---|---|---|
| Convex | Mannequin | 0.06 | 0.62 |
| Convex | Globe | 0.02 | 0.93 |
| Convex | Taj Mahal | 0.03 | 0.85 |
| Convex | Rocket | 0.02 | 0.94 |
| Convex | Star | 0.01 | 0.99 |
| Convex | Star (P.2) | 0.02 | 0.99 |
| Convex | Star (P.3) | 0.01 | 0.94 |
| Concave | Globe | 0.02 | 0.95 |
| Concave | Taj Mahal | 0.04 | 0.76 |
| Concave | Star | 0.01 | 0.98 |
| Composite | Titanic | 0.03 | 0.86 |
| Composite | Taj Mahal | 0.02 | 0.92 |
| Composite | Star | 0.01 | 1.00 |
论文在文字总结里给出总体均值:平均 Chamfer 距离约 2 cm、平均 3D F-Score 约 88.6%。并指出凸面下 Mannequin 最差(CD 6 cm、FS 62%),原因与其体积更大、更易受分辨率损失与遮挡叠加影响有关。
8. "像不像"之外的判别力:点云能否区分对象类别
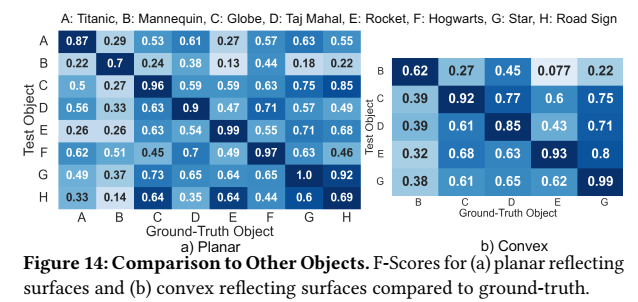
图 14 以混淆矩阵形式比较"雷达点云与其他对象真值点云"的 F-Score。行是雷达测试对象,列是真值对象;每行归一化后,理想情况是在对角线最大。论文观察到平面反射时对角线更清晰,凸面反射时混淆更强,作为"凸面反射更难"的另一种证据:即使能成像,形状细节的可辨识性仍会受到曲率导致的分辨率损失影响。
9. 微基准与扩展应用:距离、角度与长距离 BEV 绕角建图
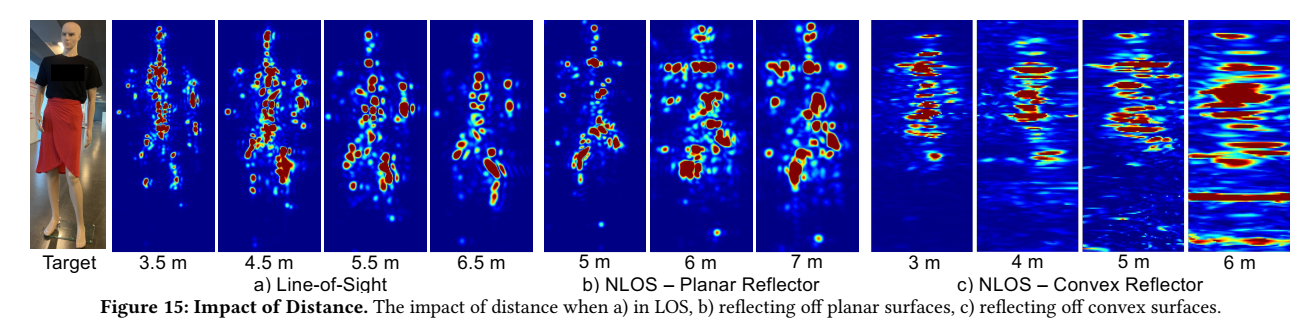
图 15 研究距离增加的影响:无论 LOS、平面反射 NLOS、凸面反射 NLOS,距离越大质量越下降,其中凸面退化最明显;但在实验中仍能在 7 m(平面)与 6 m(凸面)维持可成像输出。
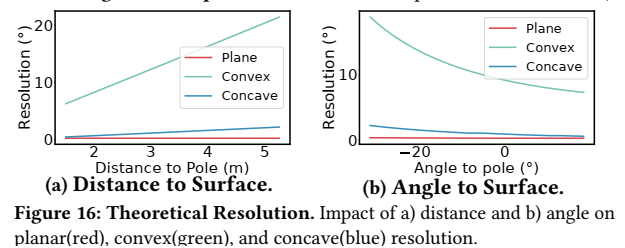
图 16 把第 6 节推导做成曲线:平面角分辨率随距离基本恒定(对应式 (8) 的不变性),凸/凹面则随距离与反射几何发生线性增长或变化。论文还指出凹面在"目标靠近且在焦点前"时可能改善分辨率,这与曲面反射存在"聚焦"条件相一致。
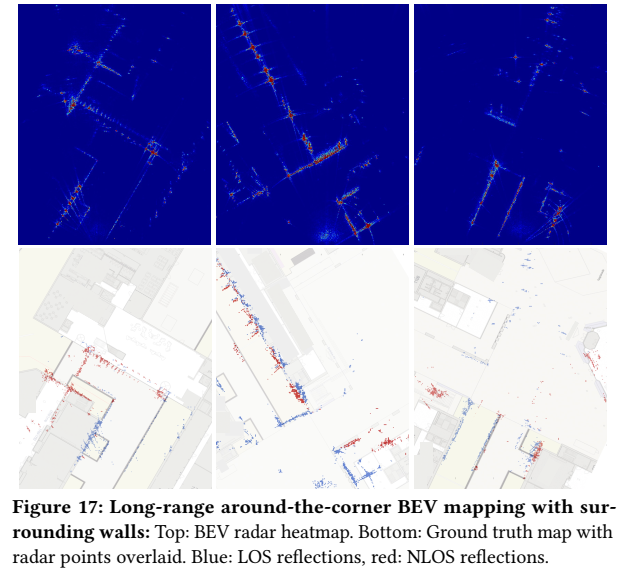
图 17 展示更偏地图构建的结果:通过对多面墙体反射几何的精确建模,把 LOS heatmap 里"墙后镜像"的反射点重新映射到真实空间,得到更大尺度的绕角 BEV 地图。图中蓝点表示 LOS 反射,红点表示 NLOS 反射,最终点云分布与真值地图接近,显示 RFlect 的框架不仅可做目标成像,也可做"利用反射的长距离环境映射"。
10. 论文自述局限:几何类别、反射假设与硬件形态
论文将局限集中在三处:目前主要覆盖 planar/convex/concave 及其组合,扩展到更不规则曲面需要更高维的 LOS 环境表征;成像依赖镜面反射假设,粗糙表面可能带来漫散射并降低质量,极化/材料等效应未纳入;原型用 SAR 扫描获得 2D 孔径,未来可用固定阵列或机器人运动替代以适配移动场景。
附录:补全原文的推导
A1. 式 (1) 的相位结构从何而来:FMCW + 频率采样的匹配滤波视角
论文直接给出式 (1),中间省略了 FMCW 体制下"距离如何进入相位"的推导。以下给出一条标准推导路径,用来解释为何会出现 ej2πcd(f+kn)e^{j\frac{2\pi}{c}d(f+kn)}ejc2πd(f+kn) 这种结构。
设发射线性调频 chirp(只写相位项):
x(t)=ej2π(f0t+γ2t2),0≤t<T, x(t)=e^{j2\pi\left(f_0 t+\frac{\gamma}{2}t^2\right)},\qquad 0\le t<T, x(t)=ej2π(f0t+2γt2),0≤t<T,
其中 f0f_0f0 为起始频率,γ\gammaγ 为调频斜率(Hz/s)。对距离为 RRR 的散射点,往返时延 τ=2R/c\tau=2R/cτ=2R/c。忽略幅度衰减与散射系数,仅写延迟回波:
y(t)=α x(t−τ)=α ej2π(f0(t−τ)+γ2(t−τ)2). y(t)=\alpha\,x(t-\tau)=\alpha\,e^{j2\pi\left(f_0 (t-\tau)+\frac{\gamma}{2}(t-\tau)^2\right)}. y(t)=αx(t−τ)=αej2π(f0(t−τ)+2γ(t−τ)2).
去斜(dechirp)做混频:z(t)=y(t) x∗(t)z(t)=y(t)\,x^*(t)z(t)=y(t)x∗(t)。代入得
z(t)=α exp{j2π(f0(t−τ)+γ2(t−τ)2−f0t−γ2t2)}=α exp{j2π(−f0τ+γ2(t2−2tτ+τ2)−γ2t2)}=α exp{j2π(−f0τ−γtτ+γ2τ2)}. \begin{aligned} z(t) &=\alpha\,\exp\Big\{j2\pi\Big(f_0 (t-\tau)+\frac{\gamma}{2}(t-\tau)^2 - f_0 t-\frac{\gamma}{2}t^2\Big)\Big\}\\ &=\alpha\,\exp\Big\{j2\pi\Big(-f_0\tau+\frac{\gamma}{2}(t^2-2t\tau+\tau^2)-\frac{\gamma}{2}t^2\Big)\Big\}\\ &=\alpha\,\exp\Big\{j2\pi\Big(-f_0\tau-\gamma t\tau+\frac{\gamma}{2}\tau^2\Big)\Big\}. \end{aligned} z(t)=αexp{j2π(f0(t−τ)+2γ(t−τ)2−f0t−2γt2)}=αexp{j2π(−f0τ+2γ(t2−2tτ+τ2)−2γt2)}=αexp{j2π(−f0τ−γtτ+2γτ2)}.
其中与 ttt 有关的项是 −γtτ-\gamma t\tau−γtτ,它对应 beat 频率 fb=γτf_b=\gamma\taufb=γτ。若在一个 chirp 内对 z(t)z(t)z(t) 取 NNN 个时间采样并做频域处理,等价于在 beat 频率上做 FFT 得到距离像;但论文采用的是更通用的"对频率采样做相位补偿并回投"的写法。将频率离散写为 fn=f+knf_n=f+knfn=f+kn(论文符号),回波相位与往返距离 d=2Rd=2Rd=2R 的关系可写成
ϕn(d)=2πc d fn, \phi_n(d)=\frac{2\pi}{c}\,d\,f_n, ϕn(d)=c2πdfn,
于是把第 iii 个天线通道的复采样记为 s(n,i)s(n,i)s(n,i),对候选体素 vvv 计算假设距离 d(v,i)d(v,i)d(v,i),做相位补偿 ejϕn(d(v,i))e^{j\phi_n(d(v,i))}ejϕn(d(v,i)) 并跨 n,in,in,i 相干累加,就得到式 (1)。这说明式 (1) 的本质是"频率维度上的距离匹配 + 阵列维度上的角匹配"的统一表达:距离模型一旦错误(例如把反射当直达),相位补偿不再一致,相干增益随之坍塌。
A2. 平面镜面反射点与式 (4) 的来源:镜像点 + 直线交平面
正文中式 (4) 用 θ=arctan(yr/xr)\theta=\arctan(y_r/x_r)θ=arctan(yr/xr) 表示 AoA,其中 (xr,yr)(x_r,y_r)(xr,yr) 是雷达与体素之间的平面镜面点。原文给出了 (xr,yr)(x_r,y_r)(xr,yr) 的解析形式但跳过了推导。其几何事实是:
平面镜面反射的折线路径等价于"到镜像点的直线路径"。
设平面 Π\PiΠ 为 n⋅p+D=0\mathbf n\cdot \mathbf p + D=0n⋅p+D=0,n\mathbf nn 为单位法向量。体素点为 v\mathbf vv,雷达点为 a\mathbf aa(论文在推导里令 a=0\mathbf a=\mathbf 0a=0)。把 v\mathbf vv 关于平面镜像,得到镜像点
v∗=v−2(n⋅v+D)n. \mathbf v^{\ast}=\mathbf v-2(\mathbf n\cdot \mathbf v + D)\mathbf n. v∗=v−2(n⋅v+D)n.
镜面点 pr\mathbf p_rpr 是直线 a→v∗\mathbf a\rightarrow \mathbf v^{\ast}a→v∗ 与平面 Π\PiΠ 的交点。令参数方程
p(t)=a+t(v∗−a). \mathbf p(t)=\mathbf a+t(\mathbf v^{\ast}-\mathbf a). p(t)=a+t(v∗−a).
代入平面方程解 ttt:
n⋅(a+t(v∗−a))+D=0⇒t=−D−n⋅an⋅(v∗−a). \mathbf n\cdot(\mathbf a+t(\mathbf v^{\ast}-\mathbf a))+D=0 \Rightarrow t=\frac{-D-\mathbf n\cdot \mathbf a}{\mathbf n\cdot(\mathbf v^{\ast}-\mathbf a)}. n⋅(a+t(v∗−a))+D=0⇒t=n⋅(v∗−a)−D−n⋅a.
于是
pr=a+t(v∗−a). \mathbf p_r=\mathbf a+t(\mathbf v^{\ast}-\mathbf a). pr=a+t(v∗−a).
当 a=0\mathbf a=\mathbf 0a=0 时,有 pr=tv∗\mathbf p_r=t\mathbf v^{\ast}pr=tv∗,其坐标展开成 (xr,yr)(x_r,y_r)(xr,yr) 后即为式 (4) 上方那组解析式。式 (4) 随后取 θ=arctan(yr/xr)\theta=\arctan(y_r/x_r)θ=arctan(yr/xr) 是因为在 2D 推导里雷达在原点,射线方向由交点坐标直接确定。
这条推导也解释了"平面反射分辨率不变"的直觉:镜像变换是刚体反射,几何关系保持,等价到镜像空间的 LOS 成像。
A3. 从式 (7) 到式 (8) 的"跳步"补全:反射矩阵保持内积
原文从式 (7) 直接给到 δθP=arccos(r1⋅r2)\delta\theta_P=\arccos(\mathbf r_1\cdot \mathbf r_2)δθP=arccos(r1⋅r2),再到 arccos(cosδθ)\arccos(\cos\delta\theta)arccos(cosδθ)。关键省略点是:为什么 r1′⋅r2′=r1⋅r2\mathbf r_1'\cdot \mathbf r_2'=\mathbf r_1\cdot \mathbf r_2r1′⋅r2′=r1⋅r2。
把反射写成矩阵形式:
r′=Rr,R=I−2nnT. \mathbf r'=\mathbf R\mathbf r,\qquad \mathbf R=\mathbf I-2\mathbf n\mathbf n^{\mathsf T}. r′=Rr,R=I−2nnT.
由于 ∥n∥=1\|\mathbf n\|=1∥n∥=1,可验证 R\mathbf RR 是正交矩阵:
RTR=(I−2nnT)T(I−2nnT)=I. \mathbf R^{\mathsf T}\mathbf R =(\mathbf I-2\mathbf n\mathbf n^{\mathsf T})^{\mathsf T}(\mathbf I-2\mathbf n\mathbf n^{\mathsf T}) =\mathbf I. RTR=(I−2nnT)T(I−2nnT)=I.
于是对任意 r1,r2\mathbf r_1,\mathbf r_2r1,r2:
r1′⋅r2′=(Rr1)T(Rr2)=r1TRTRr2=r1⋅r2. \mathbf r_1'\cdot \mathbf r_2' =(\mathbf R\mathbf r_1)^{\mathsf T}(\mathbf R\mathbf r_2) =\mathbf r_1^{\mathsf T}\mathbf R^{\mathsf T}\mathbf R\mathbf r_2 =\mathbf r_1\cdot \mathbf r_2. r1′⋅r2′=(Rr1)T(Rr2)=r1TRTRr2=r1⋅r2.
又因 r1,r2\mathbf r_1,\mathbf r_2r1,r2 是单位向量,∥r1′∥=∥r2′∥=1\|\mathbf r_1'\|=\|\mathbf r_2'\|=1∥r1′∥=∥r2′∥=1,故式 (7) 简化为
δθP=arccos(r1⋅r2). \delta\theta_P=\arccos(\mathbf r_1\cdot \mathbf r_2). δθP=arccos(r1⋅r2).
最后用三角恒等式:
r1⋅r2=cos(θ−δθ2)cos(θ+δθ2)+sin(θ−δθ2)sin(θ+δθ2)=cos(δθ), \mathbf r_1\cdot \mathbf r_2 =\cos\left(\theta-\frac{\delta\theta}{2}\right)\cos\left(\theta+\frac{\delta\theta}{2}\right) +\sin\left(\theta-\frac{\delta\theta}{2}\right)\sin\left(\theta+\frac{\delta\theta}{2}\right) =\cos(\delta\theta), r1⋅r2=cos(θ−2δθ)cos(θ+2δθ)+sin(θ−2δθ)sin(θ+2δθ)=cos(δθ),
从而得到式 (8)。
A4. 式 (11) 的来源:射线与圆的交点是一个关于 ttt 的二次方程
原文式 (11) 给出 pi,1,pi,2\mathbf p_{i,1},\mathbf p_{i,2}pi,1,pi,2 的判别式写法,推导在正文省略。设圆心 c\mathbf cc,半径 rrr,射线方向为单位向量 r\mathbf rr(对应 r1,c\mathbf r_{1,c}r1,c 或 r2,c\mathbf r_{2,c}r2,c),且射线从原点出发,则射线上点为
p(t)=tr,t≥0. \mathbf p(t)=t\mathbf r,\qquad t\ge 0. p(t)=tr,t≥0.
交圆条件为 ∥p(t)−c∥2=r2\|\mathbf p(t)-\mathbf c\|^2=r^2∥p(t)−c∥2=r2,展开:
∥tr−c∥2=(tr−c)⋅(tr−c)=t2∥r∥2−2t(c⋅r)+∥c∥2=r2. \|t\mathbf r-\mathbf c\|^2 =(t\mathbf r-\mathbf c)\cdot(t\mathbf r-\mathbf c) =t^2\|\mathbf r\|^2-2t(\mathbf c\cdot\mathbf r)+\|\mathbf c\|^2=r^2. ∥tr−c∥2=(tr−c)⋅(tr−c)=t2∥r∥2−2t(c⋅r)+∥c∥2=r2.
因 ∥r∥=1\|\mathbf r\|=1∥r∥=1,得二次方程:
t2−2(c⋅r)t+(∥c∥2−r2)=0. t^2-2(\mathbf c\cdot\mathbf r)t+(\|\mathbf c\|^2-r^2)=0. t2−2(c⋅r)t+(∥c∥2−r2)=0.
令 b=−2(c⋅r)b=-2(\mathbf c\cdot\mathbf r)b=−2(c⋅r),则写成
t2+bt+(∥c∥2−r2)=0, t^2+bt+(\|\mathbf c\|^2-r^2)=0, t2+bt+(∥c∥2−r2)=0,
判别式
d=b2−4(∥c∥2−r2), d=b^2-4(\|\mathbf c\|^2-r^2), d=b2−4(∥c∥2−r2),
解为
t=−b±d2. t=\frac{-b\pm\sqrt d}{2}. t=2−b±d .
于是交点
pi=tr=−b±d2r, \mathbf p_i=t\mathbf r=\frac{-b\pm\sqrt d}{2}\mathbf r, pi=tr=2−b±d r,
这正是式 (11) 的结构。至于凸/凹选择不同符号,本质是:在两交点中选择"位于可见弧段/可反射一侧"的那一个,使得后续法向量与反射方向满足镜面反射几何。
A5. 凸面覆盖的切线斜率:从"判别式为零"或"点到直线距离为 rrr"得到 m1,m2m_1,m_2m1,m2
原文在凸面覆盖里给出一条与圆相切的直线族,并写出 m1,2m_{1,2}m1,2 的闭式,然后用式 (17) 求夹角。推导可用"判别式为零"给出一条更可复现的路线。
假设孔径中心在原点,切线写为 y=mxy=mxy=mx。圆方程为 (x−xc)2+(y−yc)2=r2(x-x_c)^2+(y-y_c)^2=r^2(x−xc)2+(y−yc)2=r2。代入 y=mxy=mxy=mx:
(x−xc)2+(mx−yc)2=r2. (x-x_c)^2+(mx-y_c)^2=r^2. (x−xc)2+(mx−yc)2=r2.
这是关于 xxx 的二次方程:
(1+m2)x2−2(xc+myc)x+(xc2+yc2−r2)=0. (1+m^2)x^2-2(x_c+my_c)x+(x_c^2+y_c^2-r^2)=0. (1+m2)x2−2(xc+myc)x+(xc2+yc2−r2)=0.
直线与圆相切当且仅当判别式为零:
Δ=[−2(xc+myc)]2−4(1+m2)(xc2+yc2−r2)=0. \Delta=[-2(x_c+my_c)]^2-4(1+m^2)(x_c^2+y_c^2-r^2)=0. Δ=[−2(xc+myc)]2−4(1+m2)(xc2+yc2−r2)=0.
化简可得关于 mmm 的二次方程:
m2(xc2−r2)−2mxcyc+(yc2−r2)=0. m^2(x_c^2-r^2)-2m x_c y_c+(y_c^2-r^2)=0. m2(xc2−r2)−2mxcyc+(yc2−r2)=0.
从而
m1,2=2xcyc±4xc2yc2−4(xc2−r2)(yc2−r2)2(xc2−r2)=xcyc±rxc2+yc2−r2xc2−r2. m_{1,2} =\frac{2x_c y_c\pm \sqrt{4x_c^2y_c^2-4(x_c^2-r^2)(y_c^2-r^2)}}{2(x_c^2-r^2)} =\frac{x_c y_c\pm r\sqrt{x_c^2+y_c^2-r^2}}{x_c^2-r^2}. m1,2=2(xc2−r2)2xcyc±4xc2yc2−4(xc2−r2)(yc2−r2) =xc2−r2xcyc±rxc2+yc2−r2 .
得到 m1,m2m_1,m_2m1,m2 后,切线夹角由两直线斜率夹角公式推出:
θt=arctan∣m1−m21+m1m2∣, \theta_t=\arctan\left|\frac{m_1-m_2}{1+m_1m_2}\right|, θt=arctan 1+m1m2m1−m2 ,
再代入式 (18) 得 ΘC=2π−θt\Theta_C=2\pi-\theta_tΘC=2π−θt。这组推导也揭示了一个隐含可行性条件:必须满足 xc2+yc2≥r2x_c^2+y_c^2\ge r^2xc2+yc2≥r2 才有实切线(原点在圆外或圆上),否则孔径中心落在圆内,覆盖定义会变形。
A6. 原文附录 A(Alhazen 问题)中的"四次方程解"如何落到反射点 prp_rpr
论文附录 A 将"求圆上镜面点"归约为四次多项式求根,给出从复平面缩放到单位圆的表示:
z1=(x1−xc)+(y1−yc)jr,z2=(x2−xc)+(y2−yc)jr.(24) z_1=\frac{(x_1-x_c)+(y_1-y_c)j}{r},\qquad z_2=\frac{(x_2-x_c)+(y_2-y_c)j}{r}. \tag{24} z1=r(x1−xc)+(y1−yc)j,z2=r(x2−xc)+(y2−yc)j.(24)
并指出镜面点对应四次方程的四个根之一:
Au4−Bu3+Du−E=0.(25) A u^4 - B u^3 + D u - E = 0. \tag{25} Au4−Bu3+Du−E=0.(25)
附录随后引用"一般四次方程的解析解",通过变量代换把一般型变成"降次四次"(depressed quartic)。原文写出代换的一个版本(符号与排版按原文保留):
x=u−B4A,α=−3B28A2+CA,β=B38A3,γ=−3B4256A4−BD4A2+EA.(26) x=u-\frac{B}{4A},\quad \alpha=-\frac{3B^2}{8A^2}+\frac{C}{A},\quad \beta=\frac{B^3}{8A^3},\quad \gamma=-\frac{3B^4}{256A^4}-\frac{BD}{4A^2}+\frac{E}{A}. \tag{26} x=u−4AB,α=−8A23B2+AC,β=8A3B3,γ=−256A43B4−4A2BD+AE.(26)
从而得到
x4+αx2+βx+γ=0.(27) x^4+\alpha x^2+\beta x+\gamma=0. \tag{27} x4+αx2+βx+γ=0.(27)
这里原文"跳步"的关键是:如何从式 (27) 走到四个根的闭式。标准 Ferrari 方法的主线是把式 (27) 分解成两个二次式:
x4+αx2+βx+γ=(x2+px+q)(x2−px+s), x^4+\alpha x^2+\beta x+\gamma =(x^2+px+q)(x^2-px+s), x4+αx2+βx+γ=(x2+px+q)(x2−px+s),
展开并对齐系数:
{q+s−p2=α,p(s−q)=β,qs=γ. \begin{cases} q+s-p^2=\alpha,\\ p(s-q)=\beta,\\ qs=\gamma. \end{cases} ⎩ ⎨ ⎧q+s−p2=α,p(s−q)=β,qs=γ.
令 y=q+sy=q+sy=q+s(两二次常数项之和),则 p2=y−αp^2=y-\alphap2=y−α。再由 p(s−q)=βp(s-q)=\betap(s−q)=β 得 s−q=β/ps-q=\beta/ps−q=β/p。于是
q=y−β/p2,s=y+β/p2. q=\frac{y-\beta/p}{2},\qquad s=\frac{y+\beta/p}{2}. q=2y−β/p,s=2y+β/p.
代回 qs=γqs=\gammaqs=γ 得到关于 yyy 的三次方程(resolvent cubic):
(y−β/p2)(y+β/p2)=γ⇒y2−β2/p24=γ. \left(\frac{y-\beta/p}{2}\right)\left(\frac{y+\beta/p}{2}\right)=\gamma \Rightarrow \frac{y^2-\beta^2/p^2}{4}=\gamma. (2y−β/p)(2y+β/p)=γ⇒4y2−β2/p2=γ.
将 p2=y−αp^2=y-\alphap2=y−α 代入,得到
y2−β2y−α=4γ⇒y3−αy2−4γy+(4αγ−β2)=0. y^2-\frac{\beta^2}{y-\alpha}=4\gamma \Rightarrow y^3-\alpha y^2-4\gamma y+(4\alpha\gamma-\beta^2)=0. y2−y−αβ2=4γ⇒y3−αy2−4γy+(4αγ−β2)=0.
求得该三次方程的一个实根 yyy(原文用一组中间变量 P,Q,UP,Q,UP,Q,U 给出 Cardano 形式),即可得到 p=y−αp=\sqrt{y-\alpha}p=y−α ,继而得到 q,sq,sq,s,最后把四次分解为两个二次并求根。原文把这些步骤压缩成式 (28)-(29) 的中间量与根表达,并写出"通过 s,r∈{−1,1}s,r\in\{-1,1\}s,r∈{−1,1} 选择符号得到四个根"的形式。
附录还给出如何在四个根中选"物理解":对凸面,选择使镜面路径往返长度最小者:
k=argmini∈{1,2,3,4}(∣z1−ui∣+∣z2−ui∣),ur=uk,(30) k=\arg\min_{i\in\{1,2,3,4\}}\left(|z_1-u_i|+|z_2-u_i|\right),\qquad u_r=u_k, \tag{30} k=argi∈{1,2,3,4}min(∣z1−ui∣+∣z2−ui∣),ur=uk,(30)
最后将复根映射回反射点坐标:
pr=(ℜ(ur),ℑ(ur)).(31) p_r=(\Re(u_r),\Im(u_r)). \tag{31} pr=(ℜ(ur),ℑ(ur)).(31)
这条选择准则把"代数可行"过滤为"几何可行",也与费马原理一致:镜面反射路径在所有折线路径中满足驻值(在此问题下等价为最短光程的候选之一)。
A7. "凸面可用更稀疏阵列而不严重混叠"的数学轮廓:空间采样与角谱支撑
正文第 8 节的工程结论是:凸面反射导致角谱集中在一个很窄的方向扇区,因此可以增大天线间距(空间下采样)来扩孔径而不立刻出现像 LOS 那样的严重混叠。原文用语言叙述并给出"30 cm 扩到 90 cm 找回 87% 分辨率损失"的实验性数字,但省略了"为什么窄角谱允许更大间距"的数学骨架。
用一维均匀线阵解释最直接:阵列对角域的采样周期由间距 ddd 决定,其空间频率(以 sinθ\sin\thetasinθ 为变量)满足周期性。经典结论是:若希望在 sinθ∈[−1,1]\sin\theta\in[-1,1]sinθ∈[−1,1] 的全角域无混叠,需 d≤λ/2d\le \lambda/2d≤λ/2。但若信号实际只占据一个小角扇区 θ∈[θ0−Δ,θ0+Δ]\theta\in[\theta_0-\Delta,\theta_0+\Delta]θ∈[θ0−Δ,θ0+Δ],则只需保证在该支撑区内不存在"栅瓣折叠"即可,近似条件可写成
d≲λ2sin(Δ)(Δ 较小且以弧度计时 sinΔ≈Δ). d \lesssim \frac{\lambda}{2\sin(\Delta)}\qquad(\Delta\ \text{较小且以弧度计时}\ \sin\Delta\approx \Delta). d≲2sin(Δ)λ(Δ 较小且以弧度计时 sinΔ≈Δ).
因此当 Δ\DeltaΔ 很小,允许的 ddd 可显著大于 λ/2\lambda/2λ/2。凸面反射恰恰把"来自 NLOS 区域的有效到达方向"压缩到一个小角谱块里(论文也明确指出这是分辨率损失的原因),从而把"全角域无混叠"的严格条件放宽为"窄角域无混叠"的条件,这就是非均匀/稀疏阵列在凸面 NLOS 上更可行的原因。