前一段时间我们学习了STM32的外设,主页有STM32外设学习笔记。这次我们来学习一下PID算法,完事制作一个平衡车。
一.PID基本原理
1.基本原理
PID其实就是实际值快速跟踪到目标值。如果定义误差=目标值-实际值,PID任务就是尽量减少误差,把误差变为0。

为了了解PID的原理我们首先要从开环和闭环说起。
2.开环与闭环
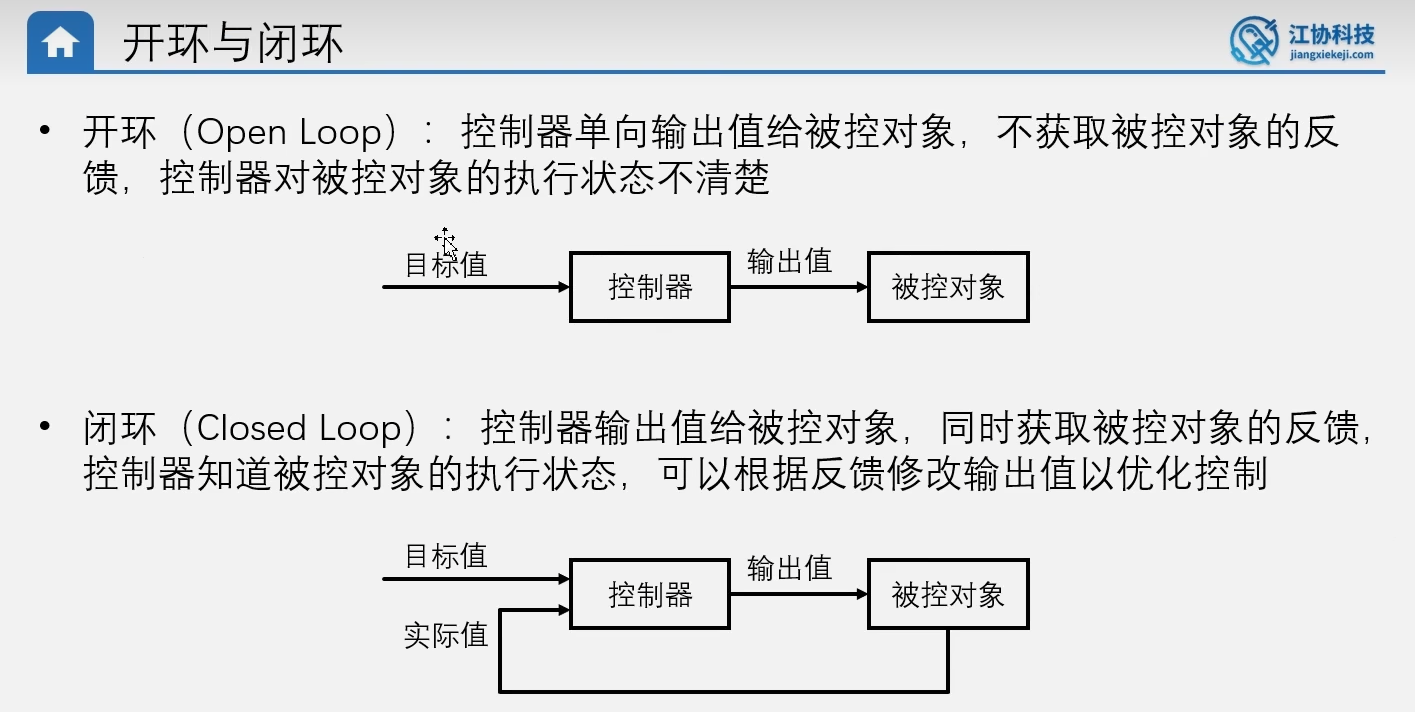
开环的话,就是目标值给到控制器,控制器直接输出,驱动被控对象。闭环的话,会把输出一部分给到输入,用于反馈,来检测电机运行状态。比如我们前面简单的PWM驱动电机的话,就是一个开环控制,PWM只会知道驱动电机,不会知道电机运动了多少。
如果给一个固定的占空比,电机负载变化,电压变化,就会不清楚。
3.PID公式与系统框图
误差的英文是:error。KP是比例系数。Ti是积分时间常数,Td是微分时间常数。
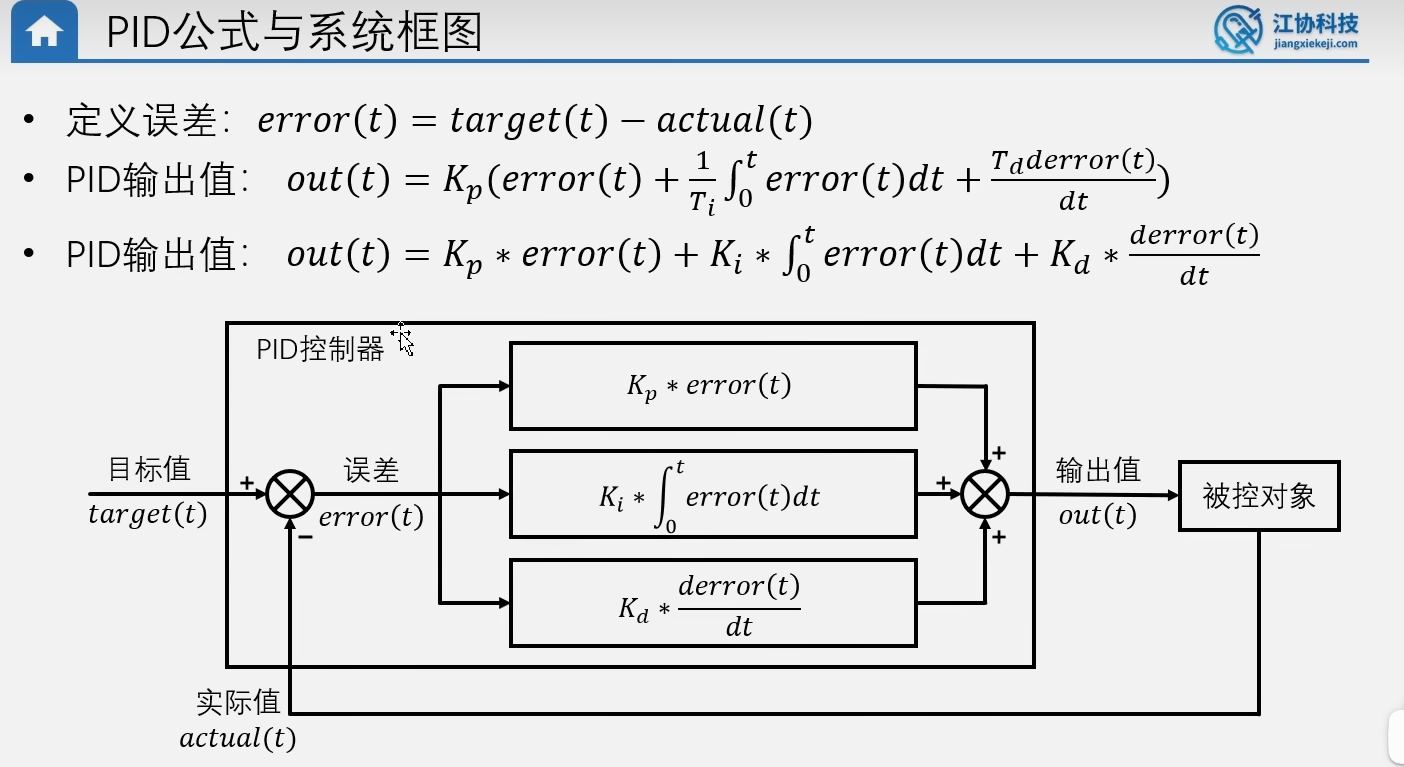
目标值和实际值进入到控制器后第一件事就是做差。error,taeget,out这三个值都带了一个(t)表示这三个值都会随着时间变化而变化。可以看到后面的公式计算的都是error,也充分说明我们上面的定义,PID是基于误差调控的算法。
Kp:比例,Ki:积分,KD:积分。
(1)比例项P
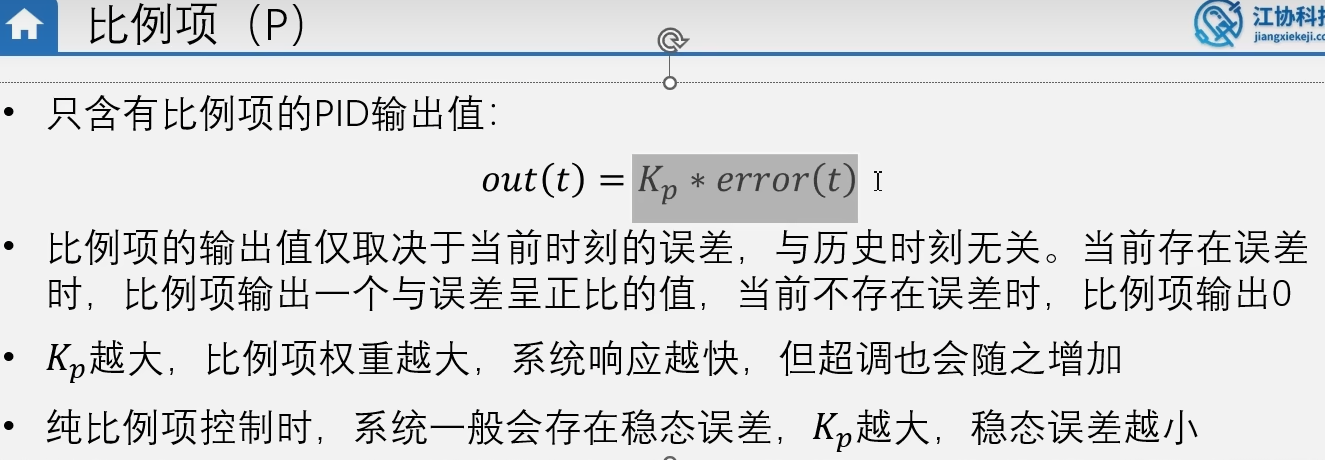
Kp表示他的调节力度。太小系统响应慢,太大系统超调严重,引起自激振荡。
(1)0.25比例
红色线表示目标速度。紫色线表示实际速度。PID的输出值直接给到PWM的占空比。可以简单理解PID的输出值,就是驱动电机旋转的力度。然后PID控制器只有比例项一个作用。
之后目标速度通过按键控制。刚开始是0,然后逐渐加到100。过一段时间归0,我们看一下不同的Kp对实际速度变化的影响。
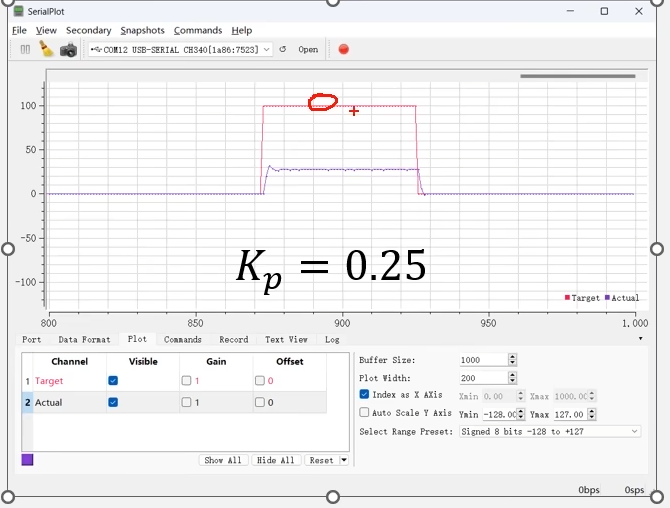
当我们设置比例系数为0.25时候,电机速度给到100,但是电机实际速度只有30左右,就不再增加了。与目标值100差了70,这差的70就是稳态误差。
(2)0.5比例
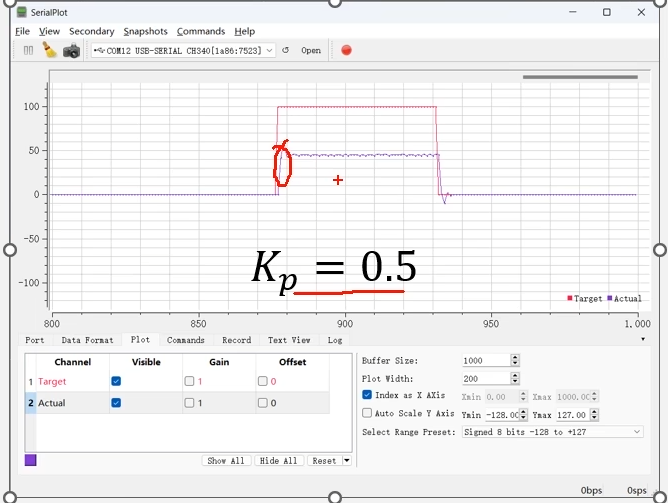
可以看到我们实际值的线,变得更陡了,意思就是速度变化更快。同时这里的超调也更大。第二个现象,我们看到稳定时候,实际速度再45附近。因此KP越大,稳态误差越小。
(3)0.75比例
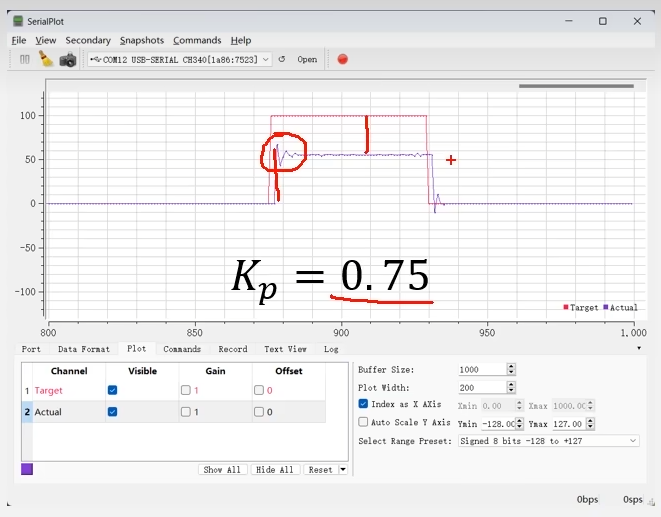
相比于前两个图,速度变化更陡峭,超调更大,稳态误差更小。这里稳态误差,可以这样理解,就是你开车的时候快到目的地了,但是你不能踩刹车,你只能松油门所以就会导致超过了。
(4)1比例
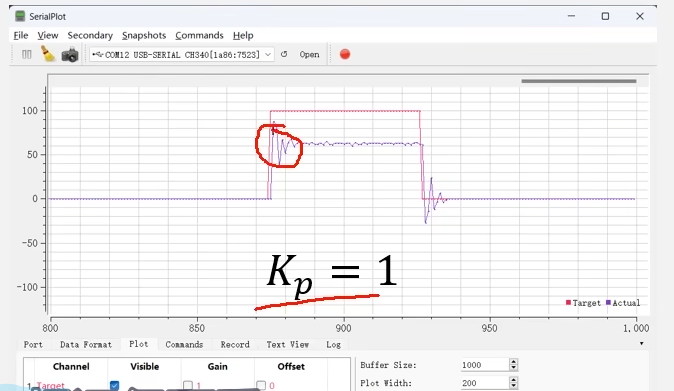
我们KP给到1,这时Kp已经过大了,超调很严重但是稳态误差仍然没有消除。
(2)稳态误差

接下来我们了解一下,为什么会有稳态误差。通过公式你可能认为,有误差PID就有输出,有输出就会减小误差,直到误差为0对吧。按理说不应该有稳态误差,为什么会是这个现象呢。

这就用到了我们稳态误差的解释。
说白了就是误差为0时,比例项直接输出为0。我们这个实验时PID的输出直接给到PWM占空比实验。也就是驱动电机的力度。如果给0的话,电机就不会维持原来的速度旋转了,因为电机有摩擦力,如果不给持续的驱动力,电机就会自发的减速,电机一减速误差就不是0了。此时电机实际速度,低于目标速度,误差为正,比例项输出值是正的。随着电机不断减速,PWM占空比会逐渐增大,也就是电机驱动力度逐渐增大,直到电机驱动力度和摩擦力平衡,系统达到稳态。
1.假设没有稳态误差,则电机实际速度=目标速度。
2.此时误差为0,PID输出为0,电机没有驱动力。
3.电机必然由于摩擦力减速,产生误差。
4.误差越大,比例项输出越大,电机驱动力度越大。
5.电机驱动力度和摩擦力平衡,电机不在减速,误差不在增大,驱动力不在增大,系统达到平衡。
匀速阶段驱动力等于摩擦力,所以驱动力Kp*error(t)等于摩擦力f(t)。因为系统摩擦力不为零,Kp也不为零,要想等式成立,error(t)自然也不能为零,也就是说误差不能为零。

判断是否会产生稳态误差。自发偏移就是摩擦力。
(3)积分项I
积分项不会单独使用,都是配合比例项使用的。

每次进行PID调空时候积分项都读取当前的error(误差),然后累加到之前所有的error之和上,所以再写积分项的程序时,程序中要单独定义一个变量,用于存储error累加的和,之后这个error累加的和,乘上一个系数Ki就是积分项的输出。
这样做的好处就是只要有积分项,就不会有稳态误差,因为系统一旦存在稳态误差,则积分项会一致累积这个误差,然后积分项的控制力度就会不断地增大。最终这个不断加大的驱动力,肯定会减小误差,直至误差为0,误差为0时,比例项直接输出0,所以此时比例项没有驱动力,但是积分项误差为0只是表示积分项的驱动力不在变化。而之前积分项累积的驱动力不会归0。所以误差为0时,积分项会有恒定的驱动力。这个力就可以对抗系统的自发偏移。所以有了积分项,系统不会有稳态误差。另外这个公式累积的时误差,所有误差累积后再×系数Ki才是输出。
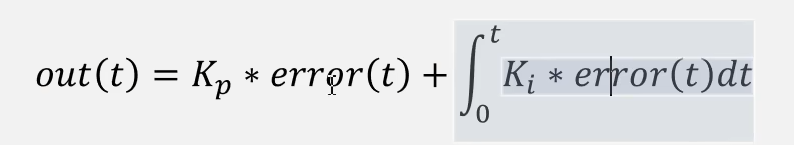
也可以这样,P项是:error×系数K,只表示当前时刻的一个驱动力。I项是error×系数K然后再积分意思就是每次的驱动力,都会累加到上次驱动力的结果上。
有一个弊端就是:因为积分项每次的输出值都是再上一次输出值的基础上累积的,假如电机控速的例子,只使用积分项控制的话,我先让电机正传到指定的速度,过一段时间后,积分项累积到了这个正转速度的驱动力。然后我突然让电机反转,那么积分项不能立刻输出反转的驱动力,他必须负向累积,把正向的消除掉,然后才能反向累积,产生反向的驱动力。这样的话,积分项的输出就慢了,这就是滞后性,滞后性带来的问题,并不是说慢一点就慢一点,影响不大。而是系统滞后会导致系统不稳定。尤其是一些平衡控制的项目。积分项加太大,系统根本不能稳定控制。
反观比例项,误差为正,比例项输出正向驱动力,误差为负,比例项立刻输出负的驱动力。比例项的反应是最快的。而且比例项的结果只取决于当前时刻的误差。与历史无关,比例项也不会累积。
(1)纯积分项
比例0,积分0.05。
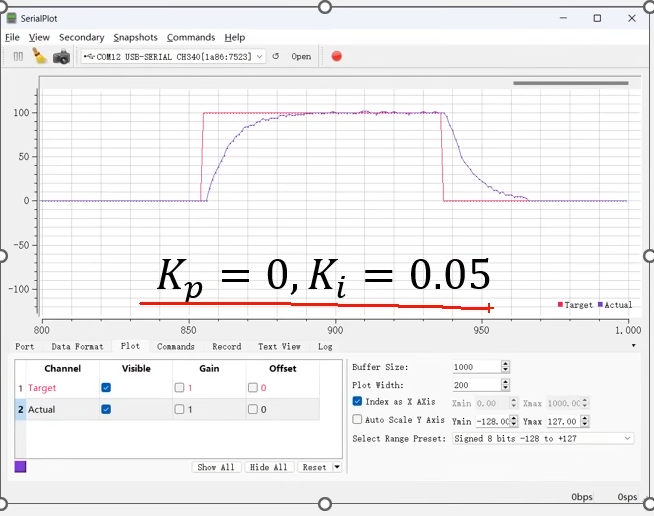
当目标速度给到100后,产生误差,积分项开始累积这个误差,产生一个不断递增的正向驱动力。这个力使得实际速度不断提生。只要有误差这个力就会不断增加,让电机不断加速,所以就不会形成稳态误差。直到目标速度和实际速度一致。误差为0积分项不在递增。

然后这一块积分的面积*Ki后输出的驱动力,正好抵消电机的摩擦力。之后就是设置目标为0,积分器开始反向积分。这就是纯积分项的模型。
(2)P,I共同控制
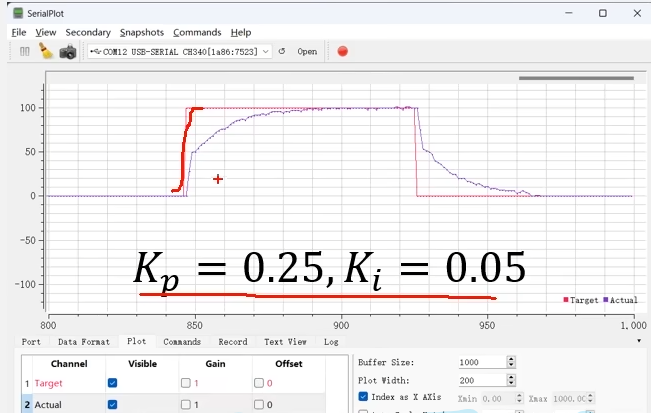
目标速度设置为100后误差为100,P项立刻输出一个正向驱动力,这个力会让实际速度立刻增加。因此这个紫色线的前段主要是P的作用。然后到上升那里,因为P项的驱动力需要对抗摩擦力,就无法再让误差减小了。接下来的过程主要靠I项发力,I项逐渐累积误差,增大驱动力,直到误差为0。误差为0时,P项没有驱动力。I项有一个稳定的驱动力,对抗摩擦力。
可以从波形看出实际上也是P和I的控制作用,前一段猛然上升就是P的波形,后一段逐渐累积上升是I的波形。单纯积分控制相应没那么快 老是调整积分常数误差累积过大就饱和了。
不过当前的波形还不太好看是因为P和I的参数没有调好。之后看中间的图。
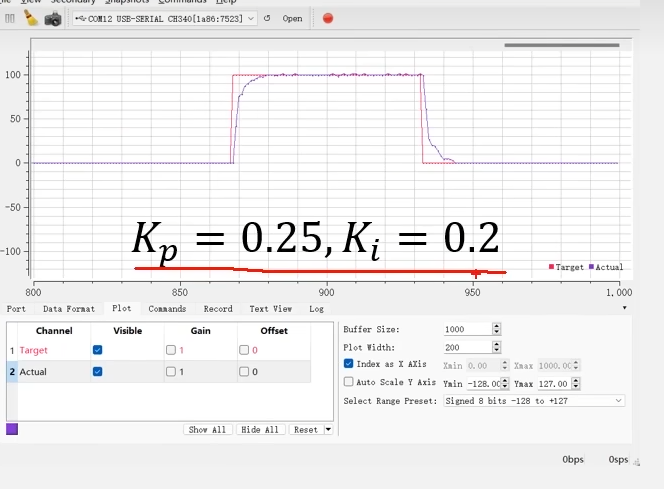
可以看到这个波形已经很接近完美了。当目标速度给到100时,P项让实际速度立刻大跨度增加。然后I项累积,弥补P项的稳态误差,两者配合在这个参属下,就比较好看了。
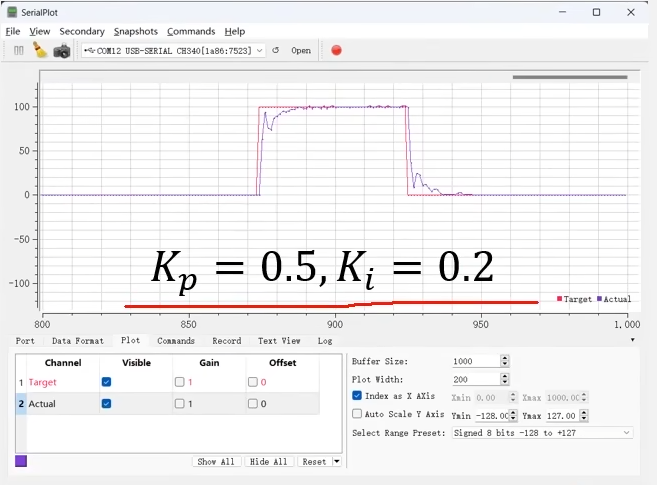
之后看到这个图,Kp=0.5和Ki=0.2。Kp调的更大,虽然这时P项的大跨步力度比较大,反应更加迅速,但是在上面产生了一些振荡。这主要是P项过大导致的,后续I项发力,消除稳态误差。但是好在速度没有超调。
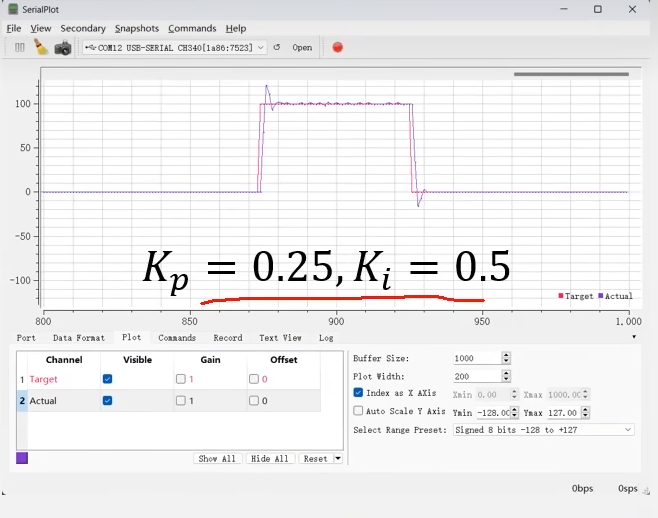
之后Kp=0.25,Ki=0.5的情况。这时Ki比较大,积分作用比较强。Kp和我们刚才这个完美的波形参数一样。由于积分作用太强,在实际速度达到目标速度这段实际累积的力太大了,这导致了超调实际速度冲出了目标速度的界限。之后反向积分,积分驱动力减小。才使得实际速度=目标速度。这里可以看出积分力过强。
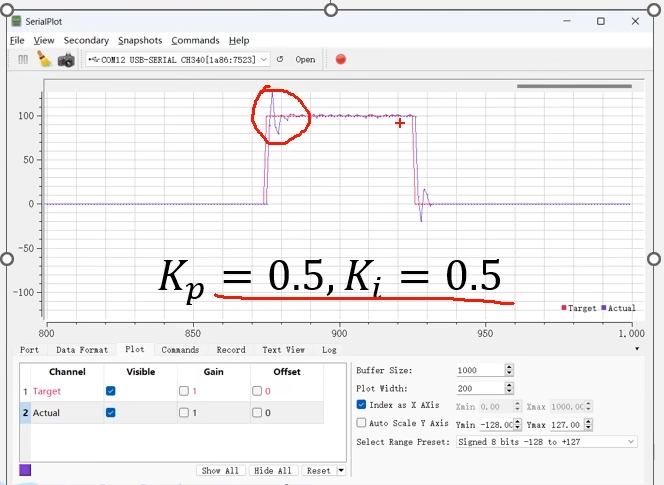
之后Kp和Ki参数都非常大,简单看一下,速度超调而且抖动也很厉害。超调是因为惯性作用。尽管实际速度反应的非常快,但是导致了超调+振荡。
(4)微分项D
微分项一般配合PI使用或者P来使用。

我们知道,微分实际上就是求导。求导实际上就是求当前点切线的斜率。实际上就是当前误差变化的速度。D项的作用就是输出相反的力,阻碍误差的急剧变化。比如说误差十分稳定一点也不变,那么斜率为0,D项输出0,如果误差向一个方向变化,那么D项就输出一个反向作用力阻碍这个变化。且变化的速度越快阻碍的力就越大。F项输出的力是阻碍误差变化,而和误差本身大小没有关系。比如当前误差是100,误差很大,但是误差恒定是100,不变化这时D项就不会输出。D项只是阻碍误差变化,并不会消除误差。
三四条就是他的作用,尤其是平衡类的项目,平衡车,四轴飞行器,倒立摆。要维持平衡D项就非常重要。
比如前面讲的P项和I项,他们只是基于当前误差和历史误差做出的调控,没有预测未来的作用,对于惯性比较大的系统很可能造成超调。并且来回持续不断的振荡。加上D项后,振荡就增加了阻尼。那么振荡就会不断衰减,系统就会变得稳定。

微分项是阻碍误差变化,所以正常P或I调控时候,D项也会阻碍他们的调控,比如D项作用过强,那么实际值的变化就会卡卡的。
(5)微分项波形
(1)微分项计算示意图
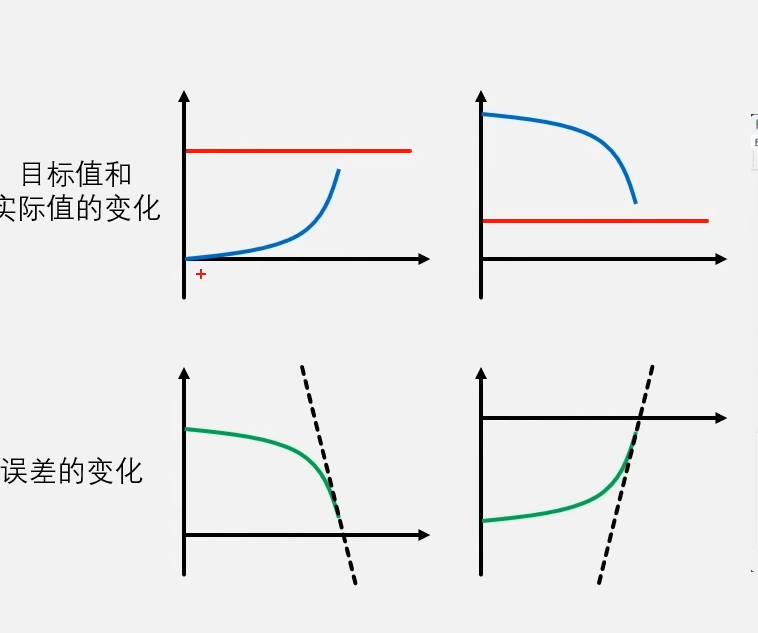
红线是设计的目标值,蓝线是实际值,这里实际值往目标值靠近的越来越快,最后直接扎向目标值按理说波形应该是离目标越近,变化的越缓慢。当实际值这样变化时,一定要加上D项的作用,因为实际值已经离目标值越来越近了,但是变化的速度还是越来越快没有放缓。那么当实际值等于目标值时,就一定会超调。加上D项后,D项的输出值取决于误差变化的频率。
下图的误差变化曲线就是用红线减去蓝线得到。在这里做个切线,可以发现斜率为负,且斜率的绝对值比较大,所以这时D项调控的输出为负向作用且作用力比较大,这个负向作用力会把实际值往下拉,这就可以避免实际值超调。
第二个图同理,上面的目标值始终小于实际值,所以误差整体是负数。然后做切线,发现切线斜率是正的,而且斜率绝对值比较大。所以D项调节力是正的,而且力度比较大。这个正向较大的力会把实际值网上拉。这样就可以尽量避免超调。
(2)倒立摆位置环变化曲线
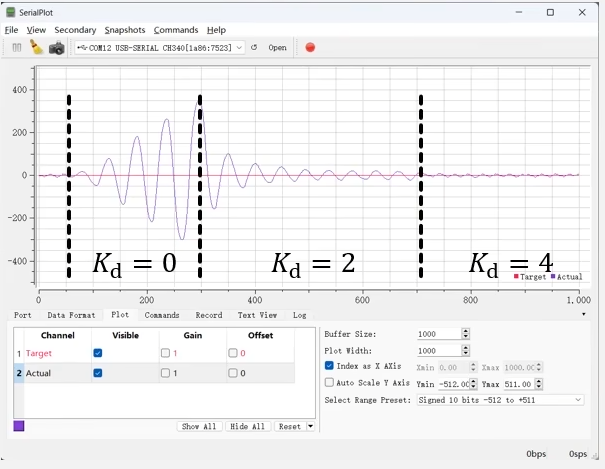
红线是目标位置始终为0。也就是要求我们位置始终固定在0位置。紫线是实际位置。
当我们把Kd设置为0也就是取消微分项作用,就可以看到倒立摆位置开始摆动起来。且每次产生误差,PI调节器都会反向调节,但是反向调节就会导致超调,产生更大的误差因为会有惯性。然后把D项作用为2,就减小了,D项的作用是加阻尼。但是Kd=2还不够,最后一点振荡衰减不了。所以我们把Kd设置为4。曲线就很平稳了。
4.总结
一般来说,对于电机的定速控制PI就足够了,一般不需要加入D控制,因为电机控速系统,一般不会来回振荡,而对于电机和倒立摆的定位置控制,可以用PD控制器,因为定位置控制一般稳态误差很小,而且是比较容易超调,来回振荡的。如果PD控制还有误差,可以加入一点点I项,这里I项不能加大了,否则定位置控制很不稳定。