1.Ruduce/规约 定义
对整个张量进行一个操作,得到一个标量结果。这个操作可以是 m a x , m i n , s u m max,min,sum max,min,sum等。
2.原理
我们用单线程的思路来实现的话,就是遍历整个张量,然后来做 r e d u c e reduce reduce的操作即可。
c
for(int i = 0; i < n; i ++){
ans = reduce_op(ans , a[i]);
}但我们这里用 c u d a cuda cuda了,想要加速,就要挖掘可并行的地方。注意到 r e d u c e reduce reduce操作是有结合律的,可以分块,计算每一块的结果,然后再合并。
那么每一块的计算,彼此之间是没有数据依赖的,是可并行的。需要同步的地方只有需要等到每一块都算完,才能开始合并。
我们这里为了简单起见,实际上实现的是,每个 b l o c k block block计算出规约结果即可,接下来把每个 b l o c k block block的结果再规约到一个标量的过程,是类似的。
3.实现
以下实现主要借鉴视频
【CUDA】Reduce规约求和(已完结~)
【CUDA】硬件与工具探索合集(更新ing)
以下的性能分析均在 R T X 4090 RTX4090 RTX4090上实现
3.0 暴力/朴素规约算法
说是暴力,但其实理解起来也没那么简单。需要理解基础的规约算法,还有线程模型
基础的规约算法思路是,每一个分块内,我们每一次,都让问题规模折半,让当前的结果数组中,元素两两进行合并。
假设初始长度是 8 8 8,那么第一次合并后结果位于 [ 0 , 2 , 4 , 6 ] [0,2,4,6] [0,2,4,6],再合并一次,结果位于 [ 0 , 4 ] [0,4] [0,4],以此类推,如下图
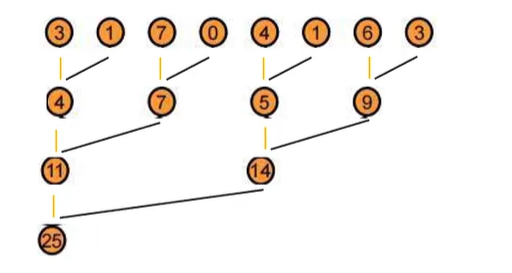
这其实类似一个位运算 t r i c k trick trick:给你一个 i n t 64 int64 int64型变量,如何在 6 6 6次位运算操作内,计算出二进制位上 1 1 1的个数的奇偶。答案是每次都 s h i f t shift shift然后异或,这和规约算法是等价的
这个过程我们的并行度在于,每一次问题规模的缩小,进行的操作都是可并行的,读,写的都是不同位置。需要同步的地方只有每一层需要全算完了,才能开始下一层。
这个算法的实现上,可以每一轮都遍历当前有效位置,让相邻的有效位置进行规约操作,想要遍历有效位置,每轮的步长需要倍增。每个分块,我们安排等同于块长的线程数,第 i i i个线程就处理第 i i i个位置的操作,所以第一轮需要操作的线程就是 0 , 2 , 4 , 6 0,2,4,6 0,2,4,6,第二轮就是 0 , 4 0,4 0,4,以此类推
当然这是第一份代码,所以我们需要搭建整体框架,包括 d e v i c e device device侧的暴力计算,资源申请,释放,调用核函数,检查结果正确性。
c
#include <stdio.h>
#define BLOCK_SIZE 256
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
__global__ void reduce(int *d_input, int *d_output)
{
//计算当前块的起始地址
int *start = d_input + blockIdx.x * blockDim.x;
for (int i = 1; i < blockDim.x; i *= 2)
{
if (threadIdx.x % (i * 2) == 0)
{
start[threadIdx.x] += start[threadIdx.x + i];
}
//每层需要同步 全算完了才能进入下一层
__syncthreads();
}
//全部计算完了,0号线程保存的就是这个块的结果,拷贝到结果数组
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = start[0];
}
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / BLOCK_SIZE;
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE; j++)
{
sum += input[i * BLOCK_SIZE + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
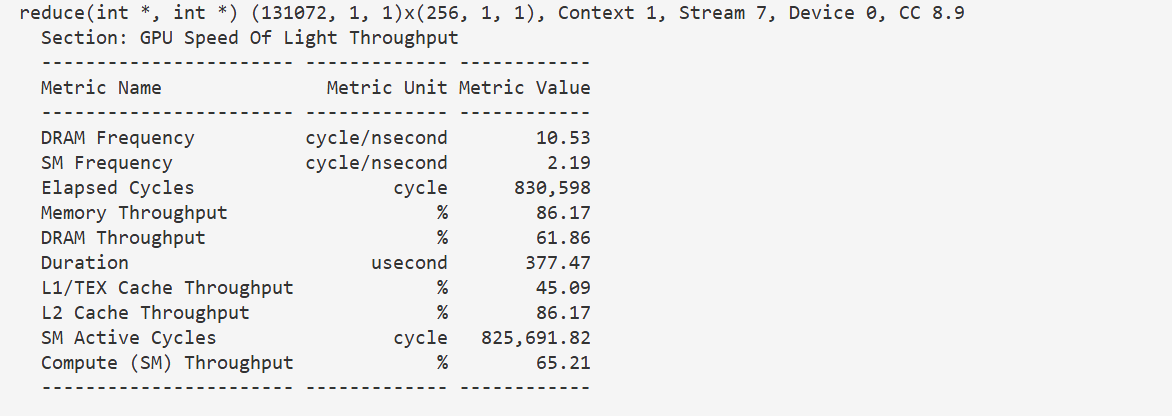
}n c u ncu ncu分析性能,看 D u r a t i o n Duration Duration字段, 377 u s 377 us 377us,以此作为基准,衡量后面的优化效果
3.1 使用共享内存/shared_memory
一个比较显然的优化是,上一份代码中,我们操作的都是全局内存,但每个块都只用自己块内的数据,那么可以把每个块的数据拷贝到自己的共享内存中,访问速度更快。
这个简单的优化其实包含一个深刻的思想:局部性和缓存。在 G P U GPU GPU编程诞生前,人们很早就意识到程序的空间局部性,因此发明了层次存储结构和多级缓存,把频繁访问的数据放在访问速度更快的缓存中,只不过操作缓存的接口,并没有留给编程开发者,而是留给系统自行调度,开发者想要利用这个局部性,只能通过调整数组存储顺序,或者在遍历时进行分块来实现
c
//调整存储顺序
for(int i = 0; i < n; i ++){
for(int j = 0; j < m; j ++){
//ans += a[j][i];
ans += a[i][j];
}
}
//分块
//for(int i = 0; i < n; i ++){
//
//}
for(int i = 0; i < n/B; i += B){
for(int j = 0; j < B; j ++){
}
}c u d a cuda cuda的共享内存其实就是一个高速缓存,并且把操作缓存的权限给了开发者,于是我们如果知道每个线程块内,频繁使用的数据是哪些,就可以直接拷贝进去,而不需要等着编译器或者操作系统来给我们优化
c
#include <stdio.h>
#define BLOCK_SIZE 256
// 使用共享内存
__global__ void reduce1(int *d_input, int *d_output)
{
// 计算全局内存下标,拷贝到共享内存
int *start = d_input + blockIdx.x * blockDim.x;
__shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x];
//拷贝这里也需要同步
__syncthreads();
for (int i = 1; i < blockDim.x; i *= 2)
{
if (threadIdx.x % (i * 2) == 0)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / BLOCK_SIZE;
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE; j++)
{
sum += input[i * BLOCK_SIZE + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce1<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
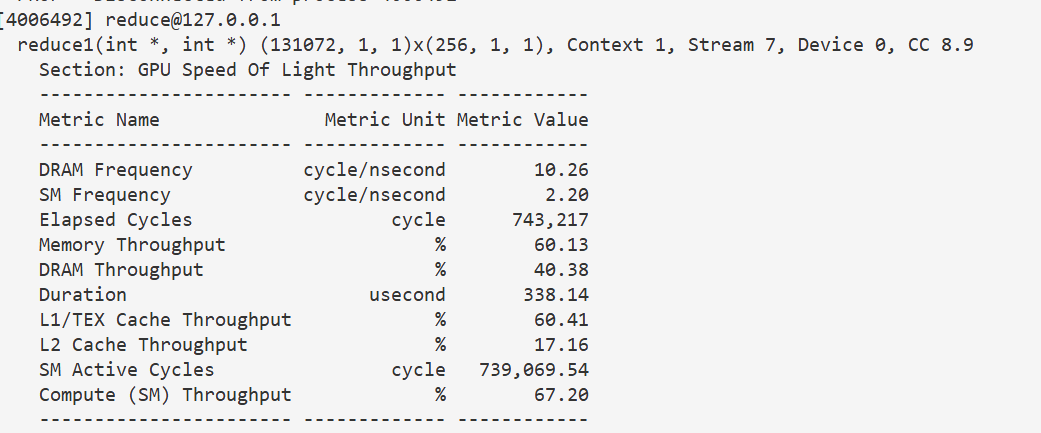
}338 u s 338 us 338us,有一定效果,不是很明显主要是因为我么访存次数不算太多,共享内存的读取加速,没有掩盖掉从全局内存拷贝到贡献内存的开销。如果是 g e m m gemm gemm之类访存很多的算子,加速效果才会比较明显
3.2 消除 线程束分化/warp_diverse
进一步的优化需要我们理解 c u d a cuda cuda的执行过程。
c u d a cuda cuda的多线程执行过程,实际上是每次取出一个 b l o c k block block内的 32 32 32个线程,组成一个线程束 w a r p warp warp,然后统一执行,这里一个问题:一个 w a r p warp warp内的线程,如果执行的操作不一样怎么办?比如有个分支指令,一部分线程进入了 A A A分支,一部分进入了 B B B分支?
答案是这两部分之间会退化成串行的,如下图
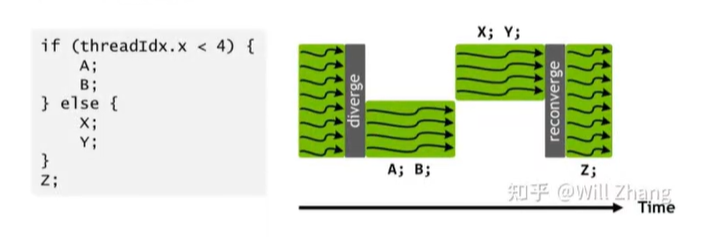
来看一下我们目前的实现没有没线程束分化,我们前面说了,我们是让第 i i i个线程,负责第 i i i个位置,那么在第一轮中 0 , 2 , . . 30 0,2,..30 0,2,..30这些线程是有运算的,其余是没有运算的,走的是两个不同分支,第二轮中 0 , 4 , . . . , 28 0,4,...,28 0,4,...,28这些线程是有运算的,其余是不进行运算的,也是走了两个不同分支。可以看到是有线程束分化的。
c
for (int i = 1; i < blockDim.x; i *= 2)
{
if (threadIdx.x % (i * 2) == 0)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
}我们想避免这一点,去掉分支指令是不太可能的,但是可以让一个 w a r p warp warp内的分支结果全都相同。仔细来看产生分化的地方,如果一共有 64 64 64个元素,第一轮执行运算的线程是 0 , 2 , 4.. , 62 0,2,4..,62 0,2,4..,62,这里只用了 32 32 32个线程,我们可以让前 32 32 32个线程 0 , 1 , . . , 31 0,1,..,31 0,1,..,31来执行这些运算操作,然后后 32 32 32个线程不执行运算操作,这样,两个 w a r p warp warp内的线程就都无分化了
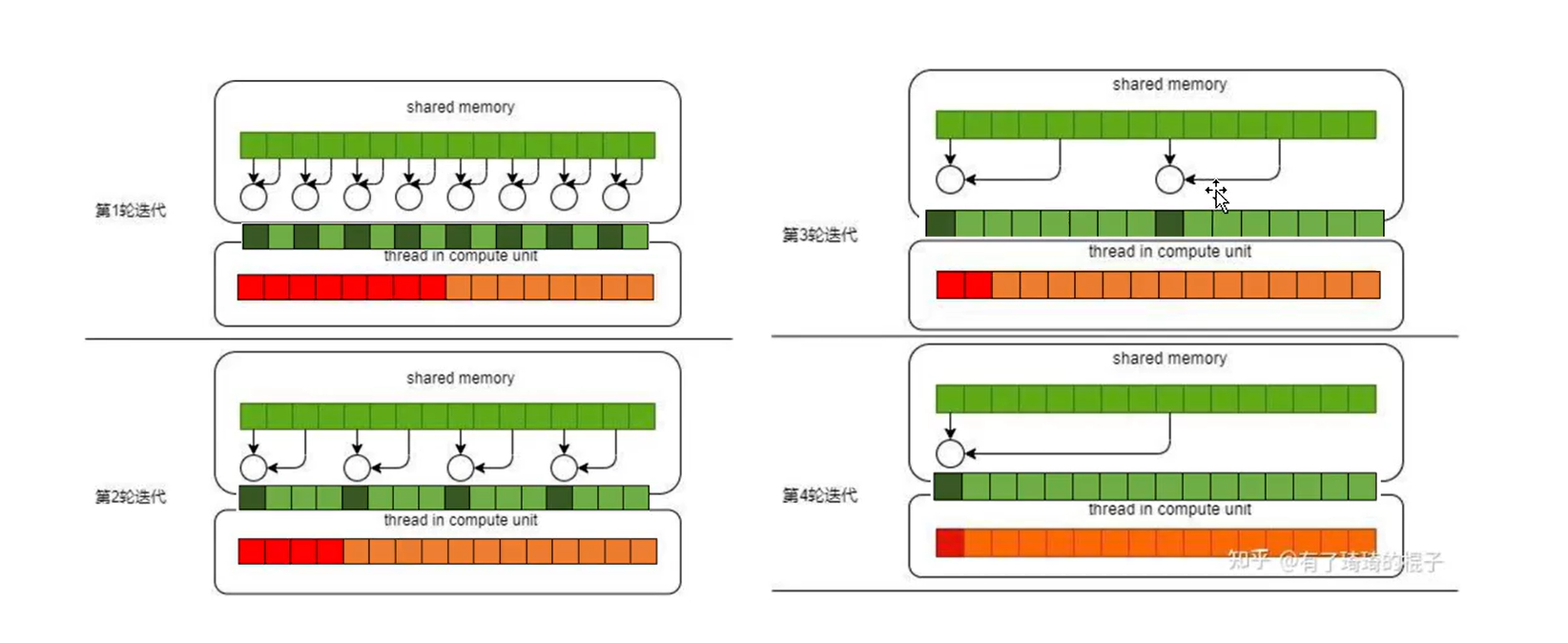
这里在实现上,线程 i i i负责的位置就不再是 i i i了,而是需要计算的,我们计算出这个下标 i d x idx idx,看他是否超出当前线程块的大小,如果不超,说明这个线程需要进行运算操作,超出则说明不需要,这样我们每轮执行运算操作线程,都是从 0 0 0号线程开始的一段,就能消除线程束分化了。
如下图,红色和橙色分别表示有无计算操作的线程
c
#include <stdio.h>
#define BLOCK_SIZE 256
// 使用共享内存
// 消除wrap分化
__global__ void reduce2(int *d_input, int *d_output)
{
// 计算全局内存下标,拷贝到共享内存
int *start = d_input + blockIdx.x * blockDim.x;
__shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x];
__syncthreads();
for (int i = 1; i < blockDim.x; i *= 2)
{
int idx = threadIdx.x * i * 2;
if (idx < BLOCK_SIZE)
{
sdata[idx] += sdata[idx + i];
}
__syncthreads();
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / BLOCK_SIZE;
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE; j++)
{
sum += input[i * BLOCK_SIZE + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce2<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}235 u s 235us 235us,这个效果还是比较明显的
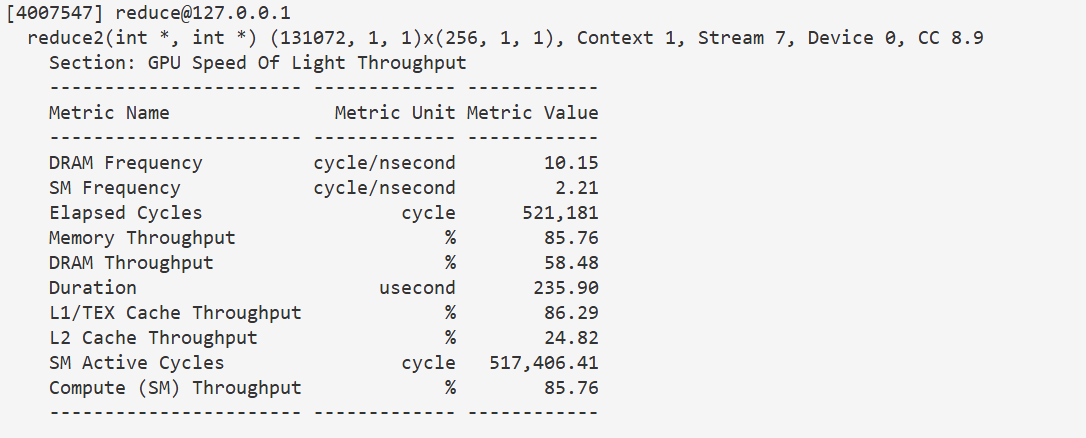
3.3 消除bank conflict
更进一步的优化需要我们了解 c u d a cuda cuda的内存架构,为了加速内存的读取,底层不是只有一个内存可读,而是把内存拆成 32 32 32份,每一份的读写时独立的,可并行,这里设计成 32 32 32也是为了配合前面提到的 w a r p warp warp中有 32 32 32个线程,理想情况下, w a r p warp warp中的每个线程,正好都去读不同的 b a n k bank bank,内存带宽提升 32 32 32倍。
比如下图, b a n k 0 bank0 bank0存的就是内存上 0 , 32 , 64 0,32,64 0,32,64这些位置的值

这里可能出现的问题是,可能多个线程会去同时读相同的 b a n k bank bank,如果有 n n n个线程去读同一 b a n k bank bank里的不同数据,称为 n n n路 b a n k bank bank冲突,那么在这个 b a n k bank bank的读就又变成串行的了。注意,如果多个线程读 b a n k bank bank里的同一数据,不会触发冲突,而是会触发广播, b a n k bank bank会把这个值广播出去,给所有需要的线程。
如下图,第二种情况在 b a n k 0 bank0 bank0,两个线程来读不同的数据,就是一个 2 2 2路 b a n k bank bank冲突,而最后两种情况,多个线程读同一个 b a n k bank bank,但是读的都是同一数据,不会冲突,而是广播
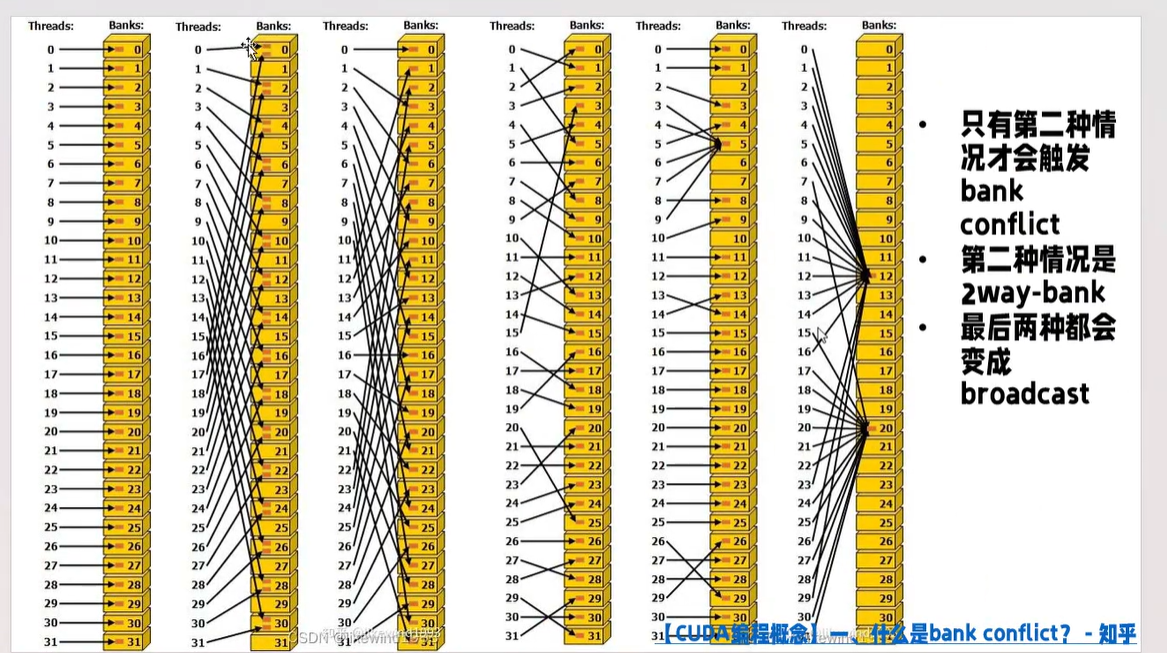
回到我们的程序,有 b a n k bank bank冲突吗?显然是有的,首先我们只用关注一个 w a r p warp warp内的线程,因为他们只有是同时执行,可能触发冲突,然后如下图, 0 , 8 , 16 , 24 0,8,16,24 0,8,16,24线程,一块取加法第一个操作数的值时,会同时访问 0 , 32 , 64 , 96 0,32,64,96 0,32,64,96的位置,触发一个至少四路的冲突
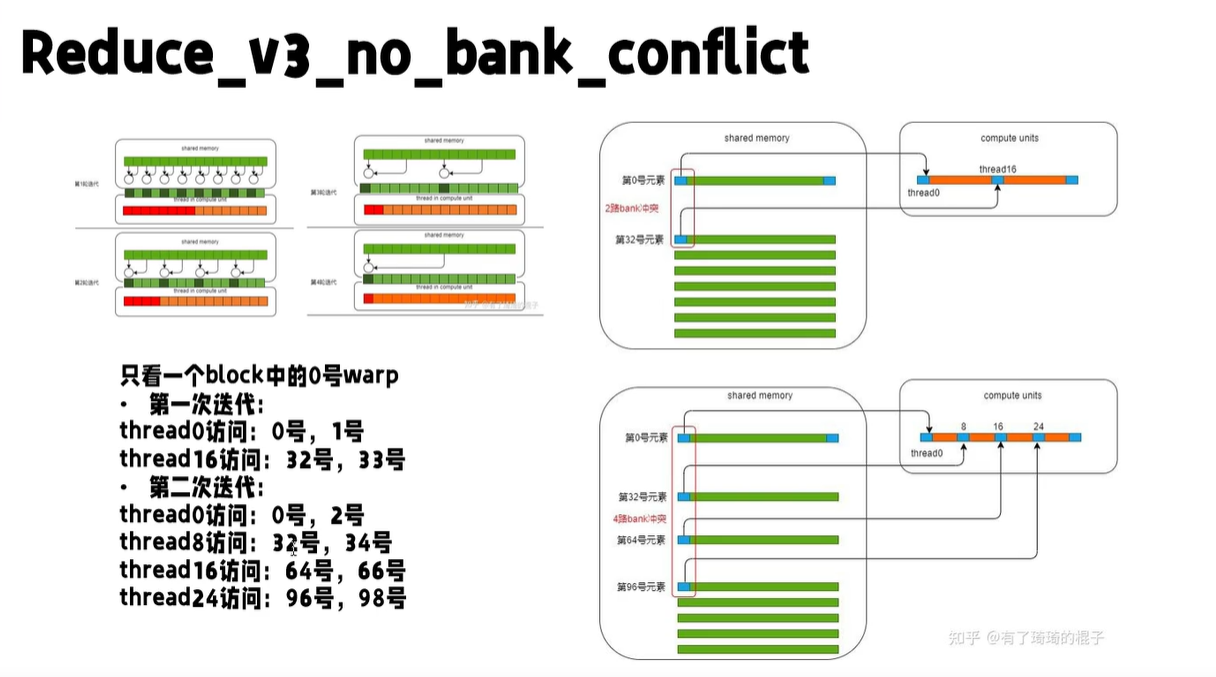
如何解决呢,可以调整每个线程负责的的元素位置,我们让每个线程负责的元素不再是相邻的两个,而是左右半区各一个,如下图,这样线程 0 , 8 , 16 , 24 0,8,16,24 0,8,16,24访问的内存就是 0 , 8 , 16 , 24 0,8,16,24 0,8,16,24了,他们之间显然是不存在冲突的。

并且之前线程编号,和负责的内存位置不是直接对应的,有点别扭,现在就简单了,线程 i i i负责的就是 i , i + s t r i d e i,i+stride i,i+stride这两个位置。 s t r i d e stride stride是当前有效元素个数的一半,每轮折半。这样实现起来也更清晰。
cpp
#include <stdio.h>
#define BLOCK_SIZE 256
// 使用共享内存
// 消除wrap分化
// 消除bank conflict
__global__ void reduce3(int *d_input, int *d_output)
{
int *start = d_input + blockIdx.x * blockDim.x;
__shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x];
__syncthreads();
// if (blockIdx.x == 1 && threadIdx.x == 0)
// {
// for (int i = 0; i < BLOCK_SIZE; i++)
// {
// printf("(%d)%d ", i, sdata[i]);
// }
// printf("\n");
// }
// 消除wrap分化
for (int i = BLOCK_SIZE / 2; i >= 1; i /= 2)
{
if (threadIdx.x < i)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
// if (blockIdx.x == 1 && threadIdx.x == 0)
// {
// for (int i = 0; i < BLOCK_SIZE; i++)
// {
// printf("(%d)%d ", i, sdata[i]);
// }
// printf("\n");
// }
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / BLOCK_SIZE;
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE; j++)
{
sum += input[i * BLOCK_SIZE + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce3<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}221 u s 221us 221us,略有提高,内存吞吐率和 S M SM SM吞吐率都提高了 5 5 5个点,还是有点效果的。
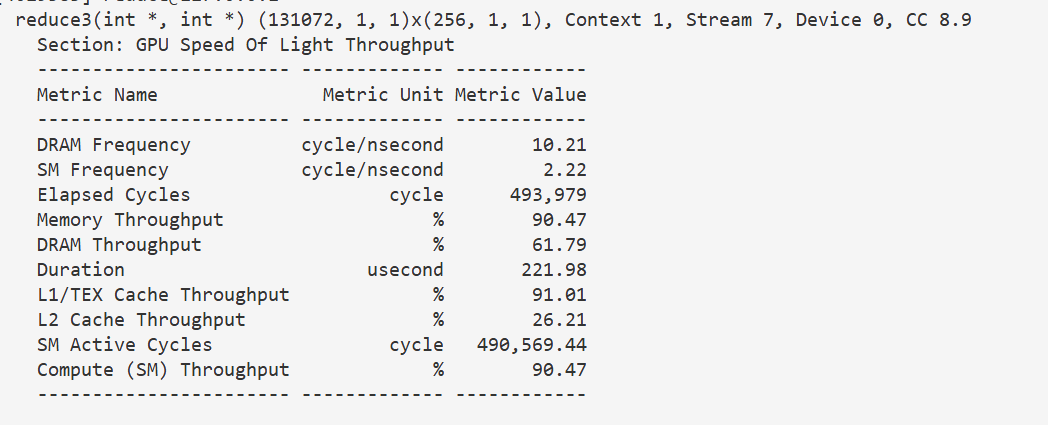
3.4 提升线程工作量(线程块个数减半)
到这一步,小优化已经提不了太多了,需要从每个线程的操作着手。
注意到按我们目前的思路,第一轮只有一半的线程有计算任务,第二轮只有四分之一的线程有计算任务,以此类推,有计算任务的线程越来越少,剩下的线程都闲着,那么一个优化思路就是来一波降本增效,把不干活的人开了。
我们可以让线程数减半,每个线程的工作量翻倍,这样虽然还是有线程闲着,但是闲着的线程数减少了。
这里有两个思路,一个是线程块个数减半,每个线程块大小不变,另一个是线程块个数不变,每个线程块大小减半。我们先实现第一个
实现起来其实也比较简单,从全局内存搬运到共享内存时,我们就让每个线程搬两个,假设有个位于线程块 i i i,块内编号 j j j的线程,就让他搬运块 i i i的 j j j位置,和块 i + 1 i+1 i+1的 j j j位置。
然后在调用核函数时把线程块个数减半,其余都不用改动。
c
#include <stdio.h>
#define BLOCK_SIZE 256
// 增加每个线程的工作量,减少block数
__global__ void reduce4(int *d_input, int *d_output)
{
int *start = d_input + blockIdx.x * blockDim.x * 2;
__shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x] + start[threadIdx.x + blockDim.x];
__syncthreads();
// 消除wrap分化
for (int i = BLOCK_SIZE / 2; i >= 1; i >>= 1)
{
if (threadIdx.x < i)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / (BLOCK_SIZE * 2);
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE * 2; j++)
{
sum += input[i * BLOCK_SIZE * 2 + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce4<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}146 u s 146us 146us,几乎减半,这还是很有效的
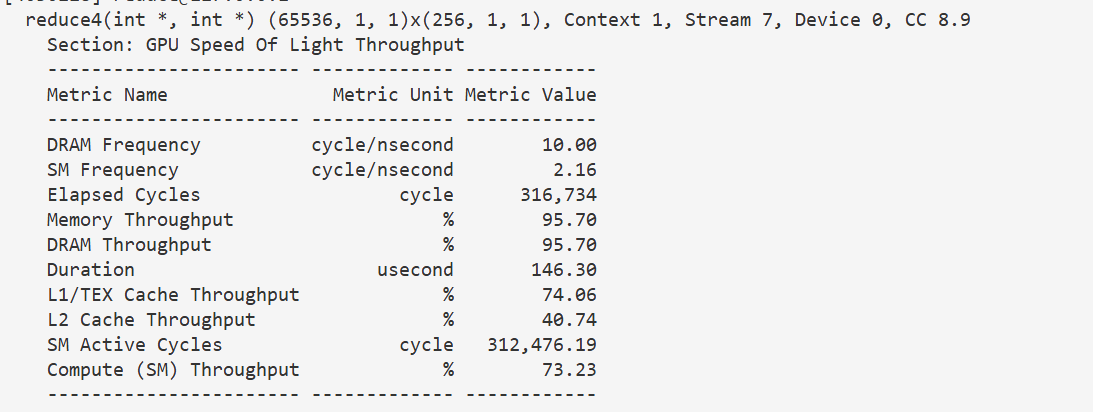
3.5 增加线程工作量(线程块大小减半)
类似地,我们也可以让线程块大小减半
注意,计算起始地址偏移量时,用的是线程块大小乘二,是因为这里的线程块大小,实际上是线程块所对应的数据块大小的一半。后面同理,搬运两个数据,另一个数据的下标加上线程块大小。
c
#include <stdio.h>
#define BLOCK_SIZE 256
// block数不变 减少block里的线程数
__global__ void reduce5(int *d_input, int *d_output)
{
int *start = d_input + blockIdx.x * blockDim.x * 2;
__shared__ int sdata[BLOCK_SIZE / 2];
sdata[threadIdx.x] = start[threadIdx.x] + start[threadIdx.x + blockDim.x];
__syncthreads();
// 消除wrap分化
for (int i = BLOCK_SIZE / 4; i >= 1; i /= 2)
{
if (threadIdx.x < i)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / BLOCK_SIZE;
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE; j++)
{
sum += input[i * BLOCK_SIZE + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE / 2);
reduce5<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i < 32 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}146 u s 146us 146us,表现差不多
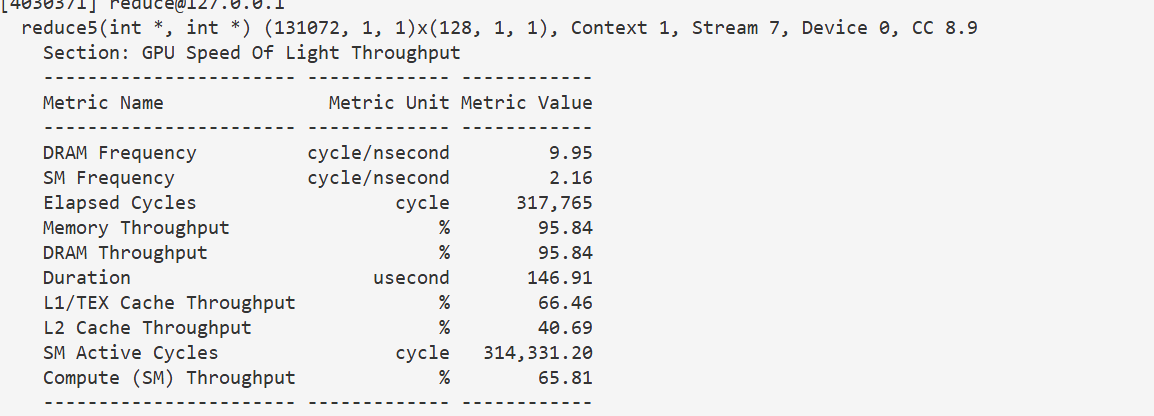
3.6 不足一个warp时循环展开
到这里其实已经没什么优化的了,基本到极限了,注意上一节的性能指标,内存吞吐量已经到了极限了。剩下的优化,如果不能改进内存读取的效率,都没什么加速。
当然,理论上这个优化还是有意义的,我们不妨实现一下。
线程同步也是一个耗时的开销,我们来考虑优化这里。注意到我们计算每一层,由于计算任务可能被分成了多个 w a r p warp warp,都要等到所有 w a r p warp warp都计算完,才能计算下一层,也就是需要一个同步。但最后有效位置不足一个 w a r p warp warp,也就是不到 32 32 32个时,只有第一个 w a r p warp warp在计算,其它 w a r p warp warp根本不干活,同步等待他们是无意义的。甚至去创建这些 w a r p warp warp都是无意义的。
所以我们可以在不足 32 32 32个元素时,不再进行循环,而是把循环展开,手动累加,这样省去同步和循环的开销。
也就是前 32 32 32个线程,执行 w a r p R e d u c e warpReduce warpReduce函数。
这里初看可能有点迷惑,因为实际上还是有数据依赖的,每一层规约要全部执行玩才能进行下一层,为什么我们这里没有同步,也不会出错呢?因为这些线程始终在一个 w a r p warp warp里,每次都只会同步的执行一个指令,也就是会先同步的执行a[tid] += a[tid + 32],再同步执行a[tid] += a[tid + 16],以此类推。 w a r p warp warp的 s i m t simt simt机制自动帮我们实现了同步。
另一个可能迷惑的点是,根据之前我们的思路,第一轮有 32 32 32个线程有计算任务,下一轮就只有 16 16 16个了,以此类推,每轮有计算任务的线程数减半,但这里我们让前 32 32 32个线程都执行了完整的 6 6 6轮规约计算,这对吗?实际上对结果无影响,我们只是让一些原本无计算任务的线程也一起执行计算了,比如第二轮, 16 − 31 16-31 16−31这些线程原本不用求和了,但现在我们也让他们进行计算了。这其实没有影响,因为从结果的角度讲 [ 16 , 31 ] [16,31] [16,31]这些位置,只有第一轮规约才会读取,后面都不用读取了,那它们的值变化了也无所谓了;从性能的角度讲,就算不给他们安排计算任务,也要跟着 w a r p warp warp里的 [ 0 , 15 ] [0,15] [0,15]线程一起计算,等待他们计算完成,那就算让 [ 15 , 31 ] [15,31] [15,31]参与计算也不会导致额外的时间开销。
这里还有一个陷阱: w a r p R e d u c e warpReduce warpReduce函数内,我们给传入的数组指针这个参数设置成了 v o l a t i l e volatile volatile,也就是不可变,这是告诉编译器,不要对这个内存的操作进行优化。这是因为这个函数内,对 a [ t i d ] a[tid] a[tid]多次读取,如果不加关键字,编译器会优化成,把 a [ t i d ] a[tid] a[tid]这个位置的值取到寄存器里,然后在寄存器内进行累加,再写回内存,这看似是对的,但我们这里是多线程,且有数据依赖的,每一轮规约后 a [ t i d ] a[tid] a[tid]的值都是会变的,我们累计是要用的是最新的值,而寄存器里的值相当于是一个缓存,没有同步到最新的值,结果就错了。加上不可变关键字,强制每次都去共享内存重新读取,才是对的。
c
#include <stdio.h>
#define BLOCK_SIZE 256
// 有任务的线程不足一个warp时,省去同步
__device__ void warpReduce(volatile int *a, int tid)
{
a[tid] += a[tid + 32];
a[tid] += a[tid + 16];
a[tid] += a[tid + 8];
a[tid] += a[tid + 4];
a[tid] += a[tid + 2];
a[tid] += a[tid + 1];
}
__global__ void reduce6(int *d_input, int *d_output)
{
int *start = d_input + blockIdx.x * blockDim.x * 2;
volatile __shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x] + start[threadIdx.x + blockDim.x];
__syncthreads();
// 消除wrap分化
for (int i = BLOCK_SIZE / 2; i > 32; i /= 2)
{
if (threadIdx.x < i)
{
sdata[threadIdx.x] += sdata[threadIdx.x + i];
}
__syncthreads();
}
if (threadIdx.x < 32)
{
warpReduce(sdata, threadIdx.x);
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / (BLOCK_SIZE * 2);
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE * 2; j++)
{
sum += input[i * BLOCK_SIZE * 2 + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce6<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}145 u s 145us 145us,几乎无优化,因为内存带宽已经快用满了,瓶颈在内存。不过这其实减小了计算量,因此注意到计算吞吐率降低了。
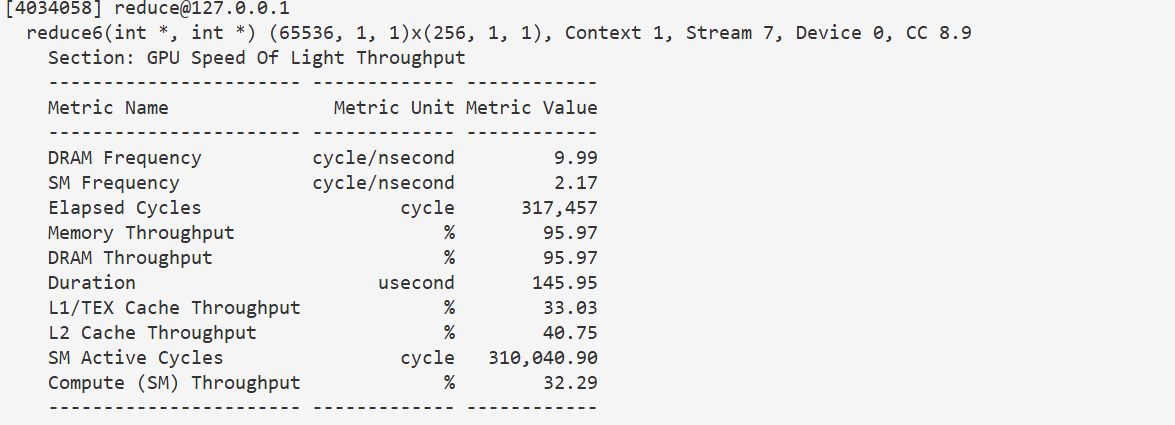
3.7 全部循环展开
根据 3.6 3.6 3.6的思路,我们其实可以把全部循环都展开,这样所有的同步都可以省去了,循环的开销也可以省去。
c
#include <stdio.h>
#define BLOCK_SIZE 256
__device__ void warpReduce(volatile int *a, int tid)
{
a[tid] += a[tid + 32];
a[tid] += a[tid + 16];
a[tid] += a[tid + 8];
a[tid] += a[tid + 4];
a[tid] += a[tid + 2];
a[tid] += a[tid + 1];
}
__global__ void reduce7(int *d_input, int *d_output)
{
int *start = d_input + blockIdx.x * blockDim.x * 2;
volatile __shared__ int sdata[BLOCK_SIZE];
sdata[threadIdx.x] = start[threadIdx.x] + start[threadIdx.x + blockDim.x];
__syncthreads();
// 消除wrap分化
if (threadIdx.x < 128)
{
sdata[threadIdx.x] += sdata[threadIdx.x + 128];
}
__syncthreads();
if (threadIdx.x < 64)
{
sdata[threadIdx.x] += sdata[threadIdx.x + 64];
}
__syncthreads();
if (threadIdx.x < 32)
{
warpReduce(sdata, threadIdx.x);
}
if (threadIdx.x == 0)
{
d_output[blockIdx.x] = sdata[0];
}
}
bool check(int *a, int *b, int N)
{
for (int i = 0; i < N; i++)
{
if (a[i] != b[i])
{
return false;
}
}
return true;
}
void solve()
{
// 申请host device侧空间
int N = 32 * 1024 * 1024;
int block_num = N / (BLOCK_SIZE * 2);
int *input = (int *)malloc(N * sizeof(int));
int *d_input;
cudaMalloc((int **)&d_input, N * sizeof(int));
int *output = (int *)malloc(block_num * sizeof(int));
int *d_output;
cudaMalloc((int **)&d_output, block_num * sizeof(int));
int *result = (int *)malloc(block_num * sizeof(int));
// 初始化值
srand(666);
for (int i = 0; i < N; i++)
{
input[i] = rand() % 1000;
}
// cpu暴力计算
for (int i = 0; i < block_num; i++)
{
int sum = 0;
for (int j = 0; j < BLOCK_SIZE * 2; j++)
{
sum += input[i * BLOCK_SIZE * 2 + j];
}
result[i] = sum;
}
cudaMemcpy(d_input, input, N * sizeof(int), cudaMemcpyHostToDevice);
dim3 Grid(block_num);
dim3 Block(BLOCK_SIZE);
reduce7<<<Grid, Block>>>(d_input, d_output);
cudaMemcpy(output, d_output, block_num * sizeof(int), cudaMemcpyDeviceToHost);
if (!check(output, result, block_num))
{
for (int i = 0; i < block_num; i++)
{
if (i == 0 && output[i] != result[i])
{
printf("blockidx:%d,output:%d,ans:%d\n", i, output[i], result[i]);
}
}
}
else
{
printf("test passed!\n");
}
cudaFree(d_output);
cudaFree(d_input);
free(input);
free(output);
free(result);
}
int main()
{
solve();
return 0;
}145 u s 145us 145us,没什么优化,但是计算吞吐量有一定的降低,计算任务确实变小了。这里应该是内存 b o u n d bound bound了,最后这几个优化,确实是优化了计算量和同步时间的,看起来没有效果主要是时间都在访存上了。
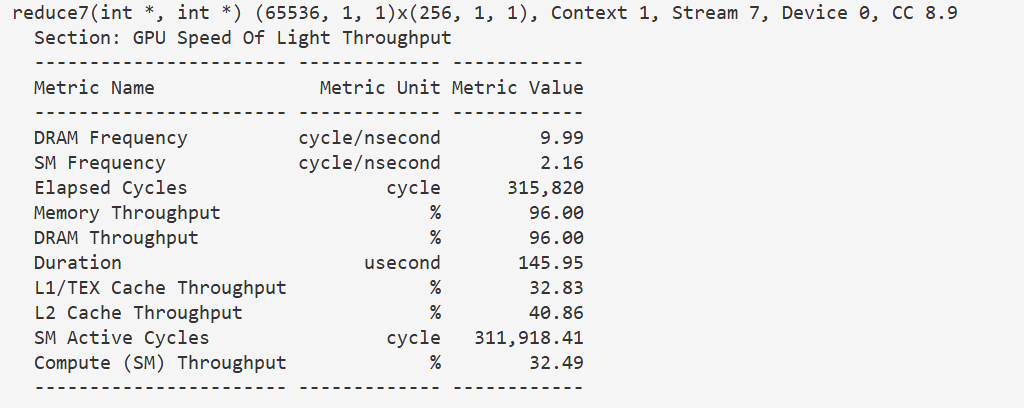
4.番外 h100上测试
4.0 朴素版本
比 4090 4090 4090还略慢,神秘
h 100 h100 h100上 n c u ncu ncu要 r o o t root root,用不了,只能 n s y s nsys nsys凑合着用,也有个核函数计时,只是单位变成 n s = 1 e − 9 s ns=1e-9s ns=1e−9s,而 n c u ncu ncu是 u s = 1 e − 6 s us=1e-6s us=1e−6s,换算一下即可,相当于 479 u s 479us 479us,比 4090 4090 4090慢百分之三十左右。

4.1 共享内存
还是比4090慢, 429 u s 429us 429us,但是优化后加速比比 4090 4090 4090要大,怀疑是 h 100 h100 h100的 H B M HBM HBM高速内存带来的加速,因为我们换到共享内存上相当于是在优化访存, H B M HBM HBM内存带宽大,优化一点访存就能提速很多

4.2 消除线程束分化
260 u s 260us 260us已经快追上4090了

4.3 消除bank冲突
199 u s 199us 199us,终于反超4090

4.4 增加线程工作量(减少线程块个数)
109 u s 109us 109us,快了一倍,比4090的 140 u s 140us 140us快很多了

4.5 增加线程工作量(减小线程块大小)
104 u s 104us 104us还要更快一点,后续优化以这个版本为基础

4.6 循环展开最后一个warp
87.4 u s 87.4us 87.4us,证明这个优化是有用的,我们前面的4090没效果完全是因为内存 b o u n d bound bound了

4.7 全部循环展开
87.1 u s 87.1us 87.1us还是有提升,可能是因为我们的线程块大小是 256 256 256,线程数超过 32 32 32的规约轮数只有两轮, 128 , 64 128,64 128,64,而且这两轮的计算,是在不同 w a r p warp warp的, w a r p warp warp间需要同步,同步的时间不能省,只剩去了 f o r for for循环的开销
