1.3.2 ⼩猫爬⼭
题⽬来源: 洛⾕
题⽬链接:P10483 ⼩猫爬⼭
难度系数: ★★
题目描述
Freda 和 rainbow 饲养了 N(N≤18) 只小猫,这天,小猫们要去爬山。经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了
Freda 和 rainbow 只好花钱让它们坐索道下山。索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1,C2,...CN。当然,每辆缆车上的小猫的重量之和不能超过 W(1≤Ci,W≤108)。每租用一辆缆车,Freda 和 rainbow 就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山?
输入格式
第一行包含两个用空格隔开的整数,N 和 W。 接下来 N 行每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,最少需要多少美元,也就是最少需要多少辆缆车。
输入输出样例
输入 #1复制
5 1996
1
2
1994
12
29输出 #1复制
2【解法】
搜索策略:依次处理每⼀只猫,对于每⼀只猫,我们都有两种处理⽅式:
• 要么把这只猫放在已经租好的缆⻋上;
• 要么重新租⼀个缆⻋,把这只猫放上去。
剪枝:
• 在搜索过程中,我们⽤全局变量记录已经搜索出来的最⼩缆⻋数量。如果当前搜索过程中,已经⽤ 的缆⻋数量⼤于全局记录的最⼩缆⻋数量,那么这个分⽀⼀定不会得到最优解,剪掉。
• 优化枚举顺序⼀:从⼤到⼩安排每⼀只猫
◦ 重量较⼤的猫能够快速把缆⻋填满,较快得到⼀个最⼩值;
◦ 通过这个最⼩值,能够提前把分⽀较⼤的情况提前剪掉。
• 优化枚举策略⼆:先考虑把⼩猫放在已有的缆⻋上,然后考虑重新租⼀辆⻋
◦ 因为如果反着来,我们会先把缆⻋较⼤的情况枚举出来,这样就起不到剪枝的效果了。
【参考代码】
cpp
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 20;
int n, w;
int c[N];//小猫当前的信息
int cnt;//当前用了多少辆车
int s[N];//每一辆车目前的总重
int ret = N; //最优解
bool cmp(int x, int y) { //用于排序
return x > y;
}
void dfs(int pos) {
if (cnt >= ret)return ;
//表示当前的车数已经大于记录的车数了
if (pos > n) { //表示每个小猫已经安排好了
ret = cnt;
return ;
}
//剪枝先安排在已有的车辆上
for (int i = 1; i <= cnt; i++) {
if (s[i] + c[pos] > w)continue; //车上已经有的小猫重量加上新来的猫大于车极限重量
s[i] += c[pos];
dfs(pos + 1);
s[i] -= c[pos];
}
cnt++;
s[cnt] = c[pos];
dfs(pos + 1);
s[cnt] = 0;
cnt--;
}
int main() {
cin >> n >> w;
for (int i = 1; i <= n; i++)cin >> c[i];
sort(c + 1, c + 1 + n, cmp);
dfs(1);
cout << ret << endl;
return 0;
}1.4 记忆化搜索
记忆化搜索也是⼀种剪枝策略。
通过⼀个"备忘录",记录第⼀次搜索到的结果,当下⼀次搜索到这个状态时,直接在"备忘录"⾥⾯找 结果。
记忆化搜索,有时也叫动态规划
【案例】
题⽬来源:⼒扣
题⽬链接:509.斐波那契数
难度系数:★
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 30
【算法原理】
在搜索的过程中,如果发现 特别多完全相同的⼦问题 ,就可以 添加⼀个备忘录 ,将搜索的结果放在备
忘录中。下⼀次在搜索到这个状态时,直接在备忘录⾥⾯拿值。
【代码实现】
cpp
class Solution {
int f[35];//搞一个备忘录
int dfs(int n)
{
if(f[n]!=-1)return f[n];//判断当前位置数据是否合法
if(n==0||n==1)return n;//递归结束条件
f[n]=dfs(n-1)+dfs(n-2);//更新
return f[n];
}
public:
int fib(int n) {
memset(f,-1,sizeof f);//先初始化成一定不会存在的值
return dfs(n);
}
};1.4.1 Function
题⽬来源: 洛⾕
题⽬链接: P1464 Function
难度系数: ★
题目描述
对于一个递归函数 w(a,b,c)
- 如果 a≤0 或 b≤0 或 c≤0 就返回值 1。
- 如果 a>20 或 b>20 或 c>20 就返回 w(20,20,20)
- 如果 a<b 并且 b<c 就返回 w(a,b,c−1)+w(a,b−1,c−1)−w(a,b−1,c)。
- 其它的情况就返回 w(a−1,b,c)+w(a−1,b−1,c)+w(a−1,b,c−1)−w(a−1,b−1,c−1)
这是个简单的递归函数,但实现起来可能会有些问题。当 a,b,c 均为 15 时,调用的次数将非常的多。你要想个办法才行。
注意:例如 w(30,−1,0) 又满足条件 1 又满足条件 2,请按照最上面的条件来算,答案为 1。
输入格式
会有若干行。
并以 −1,−1,−1 结束。
输出格式
输出若干行,每一行格式:
w(a, b, c) = ans
注意空格。
输入输出样例
输入 #1复制
1 1 1
2 2 2
-1 -1 -1输出 #1复制
w(1, 1, 1) = 2
w(2, 2, 2) = 4说明/提示
数据规模与约定
保证输入的数在 [−9223372036854775808,9223372036854775807] 之间,并且是整数。
保证不包括 −1,−1,−1 的输入行数 T 满足 1≤T≤105。
【解法】
题⽬叙述的⾮常清楚,我们仅需按照「题⽬的要求」把「递归函数」写出来即可。但是,如果不做其 余处理的话,结果会「超时」。因为我们递归的「深度」和「⼴度」都⾮常⼤。
通过把「递归展开图」画出来,我们发现,在递归过程中会遇到⼤量「⼀模⼀样」的问题,如下图
(因为递归展开过于庞⼤,这⾥只画出了⼀部分):
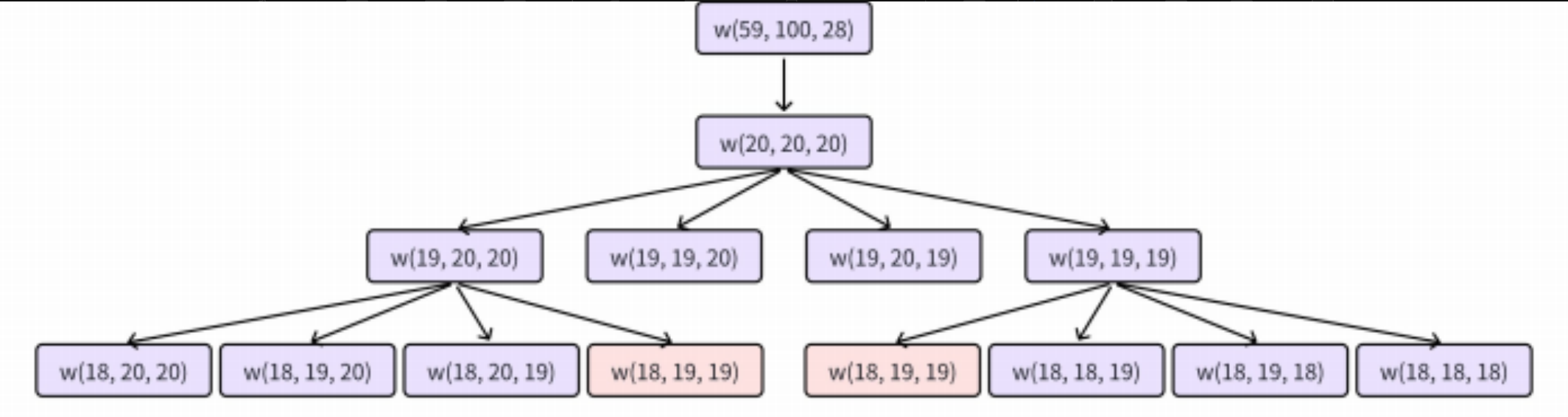
因此,可以在递归的过程中,把每次算出来的结果存在⼀张 「备忘录」 ⾥⾯。等到下次递归进⼊「⼀ 模⼀样」的问题之后,就「不⽤傻乎乎的展开计算」,⽽是在「备忘录⾥⾯直接把结果拿出来」, 起 到⼤量剪枝的效果 。
【参考代码】
cpp
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 25;
LL a, b, c;
LL f[N][N][N];//备忘录
LL dfs(LL a, LL b, LL c) {
if (a <= 0 || b <= 0 || c <= 0)return 1;
if (a > 20 || b > 20 || c > 20)return dfs(20, 20, 20);
if (f[a][b][c])return f[a][b][c];
if (a < b && b < c)return f[a][b][c] = dfs(a, b, c - 1) + dfs(a, b - 1, c - 1) - dfs(a, b - 1, c);
else return f[a][b][c] = dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a - 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);
}
int main() {
while ( cin >> a >> b >> c) {
if (a == -1 && b == -1 && c == -1)break;
printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, dfs(a, b, c));
}
return 0;
}1.4.2 天下第⼀
题⽬来源: 洛⾕
题⽬链接: P5635 【CSGRound1】天下第⼀
难度系数: ★★
题目背景
天下第一的 cbw 以主席的身份在 8102 年统治全宇宙后,开始了自己休闲的生活,并邀请自己的好友每天都来和他做游戏。由于 cbw 想要显出自己平易近人,所以 zhouwc 虽然是一个蒟蒻,也有能和 cbw 玩游戏的机会。
题目描述
游戏是这样的:
给定两个数 x,y,与一个模数 p。
cbw 拥有数 x,zhouwc 拥有数 y。
第一个回合:x←(x+y)modp。
第二个回合:y←(x+y)modp。
第三个回合:x←(x+y)modp。
第四个回合:y←(x+y)modp。
以此类推....
如果 x 先到 0,则 cbw 胜利。如果 y 先到 0,则 zhouwc 胜利。如果 x,y 都不能到 0,则为平局。
cbw 为了捍卫自己主席的尊严,想要提前知道游戏的结果,并且可以趁机动点手脚,所以他希望你来告诉他结果。
输入格式
有多组数据。
第一行:T 和 p 表示一共有 T 组数据且模数都为 p。
以下 T 行,每行两个数 x,y。
输出格式
共 T 行
1 表示 cbw 获胜,2 表示 zhouwc 获胜,error 表示平局。
输入输出样例
输入 #1复制
1 10
1 3输出 #1复制
error输入 #2复制
1 10
4 5输出 #2复制
1说明/提示
1≤T≤200。
1≤x,y,p≤10000。
【解法】
⽤ 递归模拟 整个游戏过程: dfs (x , y ) 的结果可以由 dfs ((x + y ) % p , (x + y + y ) % p) 得到。
因为测试数据是多组的,并且模数都是 p ,再加上递归的过程中会递归的相同的问题,所以可以把递 归改写成 记忆化搜索 。
其中**:** • f[x][y] = 1 ,表⽰ cbw赢;
• f[x][y] = 2 ,表⽰ zhouwc赢;
• f[x][y] = 3 表⽰这个位置已经被访问过,如果没被修改成 1 或者 2 ,那就表明平局。
注意事项:
• 这道题的数据范围很⼤,⽤ 类型创建⼆维数组空间会溢出。但是我们的最终结果仅有三种情
况,所以可以⽤ 类型来存储最终结果,节省空间。
【参考代码】
cpp
#include<iostream>
using namespace std;
const int N = 1e4 + 10;
int x, y, p;
char f[N][N];//备忘录
char dfs(int x, int y) {
if (f[x][y])return f[x][y]; //剪枝
f[x][y] = 3; //这个状态已经访问过了,之后再遇到时,表示平局
if (x == 0)return f[x][y] = '1';
if (y == 0)return f[x][y] = '2';
return f[x][y] = dfs((x + y) % p, (x + y + y) % p);
}
int main() {
int T;
cin >> T >> p;
while (T--) {
cin >> x >> y;
char ret = dfs(x, y);
if (ret == '1')cout << 1 << endl;
else if (ret == '2')cout << 2 << endl;
else cout << "error" << endl;
}
return 0;
}1.4.3 滑雪
题⽬来源: 洛⾕
题⽬链接: P1434 [SHOI2002] 滑雪
难度系数: ★★
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 24−17−16−1(从 24 开始,在 1 结束)。当然 25-24-23-...-3-2-1 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 R 和列数 C。下面是 R 行,每行有 C 个数,代表高度(两个数字之间用 1 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例
输入 #1复制
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9输出 #1复制
25说明/提示
对于 100% 的数据,1≤R,C≤100。
【解法】
暴⼒枚举 :遍历整个矩阵,看看以当前位置为起点,最远能滑⾏多远的距离。在所有情况⾥⾯,取最 ⼤值即可。
如何求出以 [i, j] 为起点的最⼤距离?
• 从[i, j] 位置上下左右瞅⼀瞅,如果能滑过去,就看看以下⼀个位置为起点,最远能滑⾏多远的距
离;
• 找出四个⽅向上的最远距离,然后 +1 。
因为出现相同⼦问题,所以可以⽤ 来解决。⼜因为在搜索的过程中会遇到⼀模⼀样的问题,因此
可以把递归改成记忆化搜索的⽅式。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 110; // 矩阵最大尺寸(题目R/C≤100,110足够用)
int n, m; // n=行数,m=列数
int a[N][N]; // 存储矩阵的高度(a[i][j]是第i行第j列的高度)
int f[N][N]; // 备忘录:f[i][j]表示从(i,j)出发的最长滑坡长度(算过就存,避免重复算)
// 方向数组:dx、dy配对表示"上下左右"四个方向
// dx[0]=0,dy[0]=1 → 向右;dx[1]=0,dy[1]=-1 → 向左;
// dx[2]=1,dy[2]=0 → 向下;dx[3]=-1,dy[3]=0 → 向上
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
// DFS函数:计算从(i,j)出发的最长滑坡长度
int dfs(int i, int j)
{
// 记忆化:如果f[i][j]不为0,说明已经算过,直接返回结果(不用重复算)
if(f[i][j]) return f[i][j];
// 初始长度:至少能站在当前点,所以长度是1
int len = 1;
// 遍历四个方向(上下左右)
for(int k = 0; k < 4; k++)
{
// 计算相邻点的坐标:x=当前行+方向k的行偏移,y=当前列+方向k的列偏移
int x = i + dx[k], y = j + dy[k];
// 边界判断:x/y超出矩阵范围(比如x=0或x>n),跳过这个方向
if(x < 1 || x > n || y < 1 || y > m) continue;
// 高度判断:相邻点高度≥当前点,不能滑过去,跳过
if(a[i][j] <= a[x][y]) continue;
// 递归计算:从(x,y)出发的最长长度 + 1(加上当前点),更新len为最大值
len = max(dfs(x, y) + 1, len);
}
// 把计算结果存到备忘录,下次再问(i,j)的最长长度,直接返回
return f[i][j] = len;
}
int main()
{
// 第一步:输入矩阵的行数n和列数m
cin >> n >> m;
// 第二步:输入矩阵的高度数据(i从1到n行,j从1到m列)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> a[i][j];
// 第三步:枚举每个点作为起点,计算最长路径,取最大值
int ret = 1; // 初始最长长度至少是1(单个点)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
ret = max(ret, dfs(i, j)); // 更新最长长度
// 第四步:输出最长滑坡长度
cout << ret << endl;
return 0;
}2. 宽度优先搜索 - BFS
宽度优先搜索的过程中,每次都会从当前点向外扩展⼀层,所以会具有⼀个最短路的特性。因此, 宽 搜不仅能搜到所有的状态,⽽且还能找出起始状态距离某个状态的最⼩步数。
但是,前提条件是每次扩展的代价都是 ,或者都是相同的数。 宽搜常常被⽤于解决边权为 的最
短路问题。
2.1 BFS
2.1.1 ⻢的遍历
题⽬来源: 洛⾕
题⽬链接:P1443 ⻢的遍历
难度系数: ★★
题目描述
有一个 n×m 的棋盘,在某个点 (x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。
输入格式
输入只有一行四个整数,分别为 n,m,x,y。
输出格式
一个 n×m 的矩阵,代表马到达某个点最少要走几步(不能到达则输出 −1)。
输入输出样例
输入 #1复制
3 3 1 1输出 #1复制
0 3 2
3 -1 1
2 1 4 说明/提示
数据规模与约定
对于全部的测试点,保证 1≤x≤n≤400,1≤y≤m≤400。
2022 年 8 月之后,本题去除了对输出保留场宽的要求。为了与之兼容,本题的输出以空格或者合理的场宽分割每个整数都将判作正确。
【解法】
题⽬要求到达某个点最少要⾛⼏步,因此可以⽤ bfs 解决。因为当权值为 1时,bfs 每次都是扩展
距离起点等距离的⼀层,天然具有最短性。
那就从起点开始,⼀层⼀层的往外搜,⽤⼀个 dist数组 记录最短距离。
【参考代码】
cpp
#include <iostream>
#include <queue> // BFS需要用到队列(queue)
#include <cstring> // 用到memset函数(初始化数组)
using namespace std;
// 定义PII:存储坐标(first=行,second=列),简化代码
typedef pair<int, int> PII;
const int N = 410; // 棋盘最大尺寸(题目n/m≤400,410足够用)
int n, m, x, y; // n=行数,m=列数,(x,y)=马的初始位置
int dist[N][N]; // 距离数组:dist[i][j]表示马到(i,j)的最少步数,-1表示不能到达
// 马的8个移动方向(走"日"字的所有可能)
// 比如dx[0]=1, dy[0]=2 → 向右下走(行+1,列+2);dx[1]=2, dy[1]=1 → 向右下走(行+2,列+1)
int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};
int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};
// BFS函数:从起点(x,y)出发,计算所有点的最短步数
void bfs()
{
// 初始化dist数组:所有值设为-1(表示初始时都未到达)
memset(dist, -1, sizeof dist);
// 创建队列q,存储待扩展的坐标(PII类型)
queue<PII> q;
// 起点入队:把初始位置(x,y)加入队列
q.push({x, y});
// 起点步数设为0(马一开始就在这,不用走)
dist[x][y] = 0;
// 队列不为空时,持续扩展
while(q.size())
{
// 取出队列头部的坐标(当前要处理的点)
auto t = q.front();
q.pop(); // 从队列中删除该点
// 解析当前点的行i、列j
int i = t.first, j = t.second;
// 遍历马的8个移动方向
for(int k = 0; k < 8; k++)
{
// 计算移动后的新坐标(x,y)
int x = i + dx[k], y = j + dy[k];
// 边界判断:新坐标超出棋盘范围(比如x<1或x>n),跳过这个方向
if(x < 1 || x > n || y < 1 || y > m) continue;
// 已访问判断:如果dist[x][y]≠-1,说明该点已经算过最短步数,跳过
if(dist[x][y] != -1) continue;
// 计算新点的步数:当前点步数+1(马走一步到达)
dist[x][y] = dist[i][j] + 1;
// 新点入队,后续扩展它的8个方向
q.push({x, y});
}
}
}
int main()
{
// 第一步:输入n, m, x, y(马的初始位置)
cin >> n >> m >> x >> y;
// 第二步:执行BFS,计算所有点的最短步数
bfs();
// 第三步:输出n×m的距离矩阵
for(int i = 1; i <= n; i++) // 遍历每一行
{
for(int j = 1; j <= m; j++) // 遍历每一列
{
cout << dist[i][j] << " "; // 输出当前点的步数,空格分隔
}
cout << endl; // 一行输出完,换行
}
return 0;
}2.1.2 kotori和迷宫
题⽬来源: ⽜客⽹
题⽬链接: kotori和迷宫
难度系数: ★★
链接:https://ac.nowcoder.com/acm/problem/50041
来源:牛客网
题目描述
kotori在一个n*m迷宫里,迷宫的最外层被岩浆淹没,无法涉足,迷宫内有k个出口。kotori只能上下左右四个方向移动。她想知道有多少出口是她能到达的,最近的出口离她有多远?
输入描述:
第一行为两个整数n和m,代表迷宫的行和列数 (1≤n,m≤30)
后面紧跟着n行长度为m的字符串来描述迷宫。'k'代表kotori开始的位置,'.'代表道路,'*'代表墙壁,'e'代表出口。保证输入合法。输出描述:
若有出口可以抵达,则输出2个整数,第一个代表kotori可选择的出口的数量,第二个代表kotori到最近的出口的步数。(注意,kotori到达出口一定会离开迷宫)
若没有出口可以抵达,则输出-1。示例1
输入
复制6 8 e.*.*e.* .**.*.*e ..*k**.. ***.*.e* .**.*.** *......e
6 8
e.*.*e.*
.**.*.*e
..*k**..
***.*.e*
.**.*.**
*......e输出
复制2 7
2 7说明
可供选择坐标为[4,7]和[6,8],到kotori的距离分别是8和7步。【解法】
经典 bfs问题。
从迷宫的起点位置逐层开始搜索,每搜到⼀个点就标记⼀下最短距离。当把整个迷宫全部搜索完之
后,扫描整个标记数组,求出出⼝的数量以及最短的距离。
【参考代码】
cpp
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 35;
int n, m, x, y;
char a[N][N];
int dist[N][N];
// 上下左右四个方向偏移量
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
void bfs() {
memset(dist, -1, sizeof dist); // 初始化距离为-1(不可达)
queue<PII> q;
q.push({x, y}); // 起点入队
dist[x][y] = 0; // 起点步数为0
while (q.size()) {
auto t = q.front();
q.pop();
int i = t.first, j = t.second;
// 遍历四个方向
for (int k = 0; k < 4; k++) {
int nx = i + dx[k], ny = j + dy[k]; // 避免和全局x/y重名,改变量名
// 合法性判断:坐标在范围内 + 不是墙壁 + 未访问过
if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny] != '*' && dist[nx][ny] == -1) {
dist[nx][ny] = dist[i][j] + 1; // 记录步数
// 出口不加入队列(到达出口即离开,无需扩展)
if (a[nx][ny] == 'e') {
continue;
}
q.push({nx, ny});
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
// 关键修正:题目中起点是小写'k',不是大写'K'
if (a[i][j] == 'k') {
x = i;
y = j;
}
}
}
bfs();
int cnt = 0; // 能到达的出口数量
int ret = 1e9; // 最近出口步数(初始设为极大值)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 是出口且可达
if (a[i][j] == 'e' && dist[i][j] != -1) {
cnt++;
ret = min(ret, dist[i][j]); // 更新最短步数
}
}
}
// 输出结果
if (cnt == 0) {
cout << -1 << endl;
} else {
cout << cnt << " " << ret << endl;
}
return 0;
}2.1.3 Catch That Cow
题⽬来源: 洛⾕
题⽬链接: [USACO07OPEN] Catch That Cow S
难度系数: ★★
题目描述
FJ 丢失了他的一头牛,他决定追回他的牛。已知 FJ 和牛在一条直线上,初始位置分别为 x 和 y,假定牛在原地不动。FJ 的行走方式很特别:他每一次可以前进一步、后退一步或者直接走到 2×x 的位置。计算他至少需要几步追上他的牛。
输入格式
第一行为一个整数 t (1≤t≤10),表示数据组数;
接下来每行包含一个两个正整数 x,y (0<x,y≤105),分别表示 FJ 和牛的坐标。
输出格式
对于每组数据,输出最少步数,每组数据间用换行隔开。
输入输出样例
输入 #1复制
1
5 17输出 #1复制
4【解法】
可以暴⼒枚举出所有的⾏⾛路径,因为是求最少步数,所以可以⽤ bfs解决:
• 从起点位置开始搜索,每次向外 扩展三种⾏⾛⽅式 ;
• 当第⼀次搜到⽜的位置时,就是最短距离。
如果不做任何处理,时间和空间都会超。因为我们会搜索到很多⽆效的位置,所以我们要加上剪枝策
略:
1. 当 −1 减到负数的时候,剪掉;
因为如果⾛到负数位置,还是需要回头⾛到正数位置,⼀定不是最优解。
2. 当 +1 操作越过 y的时候,剪掉;
如果 +1 之后⼤于 y,说明本⾝就在 y位置或者 y的右侧,你再往右⾛还是需要再向左⾛回 去。⼀定不是最优解,剪掉。
3. 当 y 是偶数,并且当 ×2 操作之后⼤于 y 的时候,剪掉,因为不如先减到 y的⼀半然后再乘;
设当前数是 x,那么:
◦ 先乘后减,总的步数 t 1 = 2 x − y + 1 ;
◦ 先减后乘,总的步数 t 2 = x − y /2 + 1 ;
◦ t 1 − t 2 = 2 x − y + 1 − ( x − y /2 + 1) = x − y /2 > 0 ;
◦ 因此,先乘后减不如先减后乘。
4. 设 y 是奇数的时候,那么 y + 1 就是偶数,根据 3 可得, ×2 操作不能超过 y+ 1 。
【参考代码】
cpp
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 2e5 + 10; // 扩大范围,避免x×2越界(y≤1e5,x×2最多到2e5)
int dist[N]; // dist[pos] = 从x到pos的最少步数,-1表示未访问
// BFS函数:计算从start到target的最少步数
int bfs(int start, int target) {
memset(dist, -1, sizeof dist); // 初始化所有位置为未访问
queue<int> q;
q.push(start); // 起点入队
dist[start] = 0; // 起点步数为0
while (!q.empty()) {
int cur = q.front(); // 当前位置
q.pop();
// 终止条件:找到牛的位置,直接返回步数(BFS第一次搜到就是最短)
if (cur == target) {
return dist[cur];
}
// 方式1:前进1步(cur+1)
int next1 = cur + 1;
// 剪枝:next1不超过2e5(避免越界)+ 未访问过
if (next1 < N && dist[next1] == -1) {
dist[next1] = dist[cur] + 1;
q.push(next1);
}
// 方式2:后退1步(cur-1)
int next2 = cur - 1;
// 剪枝:next2≥0(负数无意义)+ 未访问过
if (next2 >= 0 && dist[next2] == -1) {
dist[next2] = dist[cur] + 1;
q.push(next2);
}
// 方式3:瞬移×2(cur×2)
int next3 = cur * 2;
// 剪枝:next3不超过2e5(避免越界)+ 未访问过
if (next3 < N && dist[next3] == -1) {
dist[next3] = dist[cur] + 1;
q.push(next3);
}
}
return -1; // 理论上不会执行(牛不动,必能追到)
}
int main() {
int T;
cin >> T; // 数据组数
while (T--) {
int x, y;
cin >> x >> y;
// 特判:如果FJ已经在牛的位置,步数为0
if (x == y) {
cout << 0 << endl;
continue;
}
// 执行BFS,输出最少步数
cout << bfs(x, y) << endl;
}
return 0;
}2.1.4 ⼋数码难题
题⽬来源: 洛⾕
题⽬链接: P1379 ⼋数码难题
难度系数: ★★★
题目描述
在 3×3 的棋盘上,摆有八个棋子,每个棋子上标有 1 至 8 的某一数字。棋盘中留有一个空格,空格用 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为 123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入格式
输入初始状态,一行九个数字,空格用 0 表示。
输出格式
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。
输入输出样例
输入 #1复制
283104765输出 #1复制
4说明/提示
样例解释
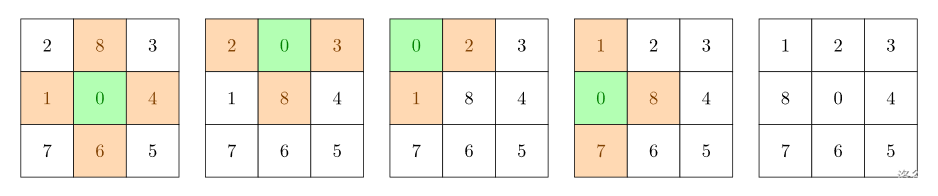
图中标有 0 的是空格。绿色格子是空格所在位置,橙色格子是下一步可以移动到空格的位置。如图所示,用四步可以达到目标状态。
并且可以证明,不存在更优的策略。
【解法】
经过之前那么多题的铺垫,这道题的解法还是容易想到的。因为要求的是 最短步数 ,因此可以⽤ bfs 解决。
• 从起始状态开始,每次扩展上下左右交换后的状态;
• 在搜索的过程中,第⼀次遇到最终状态就返回最短步数。
算法原理虽然容易,但是实现起来⽐较⿇烦,我们要想办法处理下⾯⼏件事情:
1. 如何记录⼀个 3 × 3 的棋盘?
可以⽤字符串。从上往下,从左往右将棋盘内的数依次存到⼀个字符串⾥,来标记棋盘的状态。
2. 如何记录最短路?
可以⽤ unordered_map< string,int> 来标记最短距离;
3. 如何通过⼀个字符串找到交换之后的字符串?
策略⼀:先把字符串还原成⼆维矩阵,然后交换 0 与四周的数字,最后再把交换之后的棋盘还原
成字符串。
虽然可⾏,但是太过于⿇烦。我们其实可以通过计算,快速得出⼆维坐标与⼀维下标相互转换前后
的值。如下图:
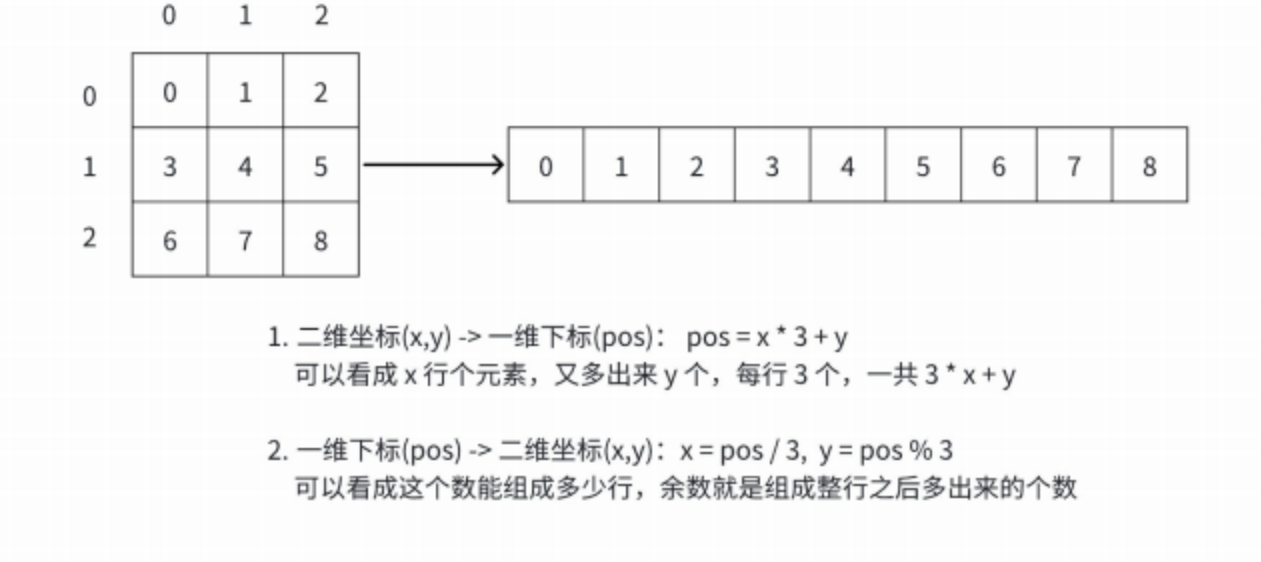
这个技巧特别常⽤, 我们可以推⼴到 的矩阵坐标 ,映射成⼀个数 ,可以起到 空间优化的效果 。后续做题中我们就会遇到。
n × m ( x , y ) pos
因此, 我们可以直接在字符串中,找出交换前后的下标,直接交换字符串对应位置,就能得到交换
之后的状态。
【参考代码】
cpp
#include <iostream>
#include <unordered_map> // 记录每个状态的最短步数(哈希表,查询快)
#include <queue> // BFS队列,存储待扩展的状态
using namespace std;
string s; // 初始状态字符串(输入的9位数字)
string aim = "123804765";// 目标状态(固定)
unordered_map<string, int> dist; // key=状态字符串,value=到该状态的最少步数
// 方向数组:上下左右(二维坐标的偏移量)
int dx[] = {0, 0, 1, -1}; // x轴偏移(行):0=右,0=左,1=下,-1=上
int dy[] = {1, -1, 0, 0}; // y轴偏移(列):1=右,-1=左,0=下,0=上
void bfs() {
queue<string> q; // BFS队列,存储待扩展的棋盘状态
q.push(s); // 初始状态入队
dist[s] = 0; // 初始状态步数为0
while (q.size()) { // 队列不为空时持续扩展
string t = q.front(); // 取出队首的当前状态
q.pop();
// 第一步:找到当前状态中空格(0)的一维下标pos
int pos = 0;
while (t[pos] != '0') pos++; // 遍历字符串,找到'0'的位置
// 第二步:把一维下标pos转换成二维坐标(x,y)
int x = pos / 3; // 行号(0~2):pos÷3取整
int y = pos % 3; // 列号(0~2):pos%3取余
// 第三步:遍历上下左右四个方向,生成新状态
for (int i = 0; i < 4; i++) {
// 计算空格移动后的新二维坐标(a,b)
int a = x + dx[i]; // 新行号
int b = y + dy[i]; // 新列号
// 边界判断:新坐标必须在3×3棋盘内(0≤a≤2,0≤b≤2)
if (a >= 0 && a <= 2 && b >= 0 && b <= 2) {
// 复制当前状态,生成新状态(避免修改原状态)
string next = t;
// 计算新坐标(a,b)对应的一维下标p
int p = 3 * a + b;
// 交换空格(pos)和新位置(p)的字符(模拟棋子移动)
swap(next[p], next[pos]);
// 剪枝:如果新状态已经访问过(dist中有记录),跳过
if (dist.count(next)) continue;
// 记录新状态的步数:当前状态步数+1
dist[next] = dist[t] + 1;
q.push(next); // 新状态入队,继续扩展
// 剪枝:如果新状态是目标状态,直接返回(BFS第一次搜到就是最短步数)
if (next == aim) return;
}
}
}
}
int main() {
cin >> s; // 输入初始状态(9位字符串,比如283104765)
bfs(); // 执行BFS,计算所有可达状态的步数
cout << dist[aim] << endl; // 输出目标状态的最少步数
return 0;
}2.2 多源 BFS
1. 单源最短路问题 vs 多源最短路问题
• 当问题中只存在⼀个起点 时,这时的最短路问题就是单源最短路问题。
• 当问题中存在多个起点⽽不是单⼀起点 时,这时的最短路问题就是多源最短路问题。
2. 多源 BFS
多源最短路问题的边权都为 1 时,此时就可以⽤多源 BFS来解决。
3. 解决⽅式
把这些源点汇聚在⼀起,当成⼀个"超级源点"。然后从这个"超级源点"开始,处理最短路问题。落实 到代码上时:
1. 初始化的时候,把所有的源点都加⼊到队列⾥⾯;
2. 然后正常执⾏ bfs 的逻辑即可。
也就是初始化的时候,⽐普通的 bfs 多加⼊⼏个起点。
2.2.1 矩阵距离
题⽬来源: ⽜客⽹
题⽬链接: 矩阵距离
难度系数: ★★
链接:https://ac.nowcoder.com/acm/problem/51024
来源:牛客网
题目描述
给定一个N行M列的01矩阵 A,A[i][j] 与 A[k][l] 之间的曼哈顿距离定义为:
dist(A[i][j],A[k][l]) =|i-k|+|j-l|
输出一个N行M列的整数矩阵B,其中:
B[i][j]=min(1≤x≤N,1≤y≤M,A[x][y]=1)B[i][j]=min(1\leq x\leq N,1\leq y\leq M,A[x][y]=1)B[i][j]=min(1≤x≤N,1≤y≤M,A[x][y]=1){dist(A[i][j],A[x][y])}
即求与每个位置曼哈顿距离最近的1
N,M≤1000N,M \leq 1000N,M≤1000
输入描述:
第一行两个整数n,m。
接下来一个N行M列的01矩阵,数字之间没有空格。输出描述:
一个N行M列的矩阵B,相邻两个整数之间用一个空格隔开。示例1
输入
复制3 4 0001 0011 0110
3 4
0001
0011
0110输出
复制3 2 1 0 2 1 0 0 1 0 0 1
3 2 1 0
2 1 0 0
1 0 0 1【解法】
正难则反:
• 如果针对某⼀个点直接去找最近的1 ,我们需要对所有的0 都来⼀次 bfs,这个时间复杂度是
接受不了的。
• 但是我们如果反着来想 ,从 1开始向外扩展 ,每遍历到⼀个0 就更新⼀下最短距离。这样仅需⼀
次 ,就可以把所有点距离的最短距离更新出来。
正难则反是很重要的思想,后续还有很多题可以⽤到这个思想。
由于1 的数量很多,因此可以把所有的1 看成⼀个超级源点,从这个超级源点开始⼀层⼀层的向外
扩展。实现起来也很简单,就是在初始化阶段把所有1 的坐标加⼊到队列中,然后正常 bfs。
【参考代码】
cpp
#include <iostream>
#include <queue> // BFS队列
#include <cstring> // memset初始化数组
using namespace std;
typedef pair<int, int> PII; // 存储坐标(行,列),简化代码
const int N = 1010; // 矩阵最大尺寸(N/M≤1000,1010足够)
int n, m; // 矩阵的行数n,列数m
char a[N][N]; // 存储输入的01矩阵(字符型)
int dist[N][N]; // 距离矩阵:dist[i][j] = (i,j)到最近1的距离,-1表示未访问
// 方向数组:上下左右四个方向(行偏移dx,列偏移dy)
int dx[] = {0, 0, 1, -1}; // 0=右,0=左,1=下,-1=上
int dy[] = {1, -1, 0, 0}; // 1=右,-1=左,0=下,0=上
void bfs() {
// 初始化距离矩阵:所有值设为-1(表示未访问)
memset(dist, -1, sizeof dist);
queue<PII> q; // BFS队列,存储待扩展的坐标
// 第一步:多源初始化------把所有1的坐标加入队列,距离设为0
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == '1') { // 找到所有1的位置
q.push({i, j}); // 入队
dist[i][j] = 0; // 1到自己的距离是0
}
}
}
// 第二步:正常BFS扩展(逐层向外)
while (q.size()) {
auto t = q.front(); // 取出队首坐标(当前处理的点)
q.pop(); // 从队列中删除
int x = t.first, y = t.second; // 解析当前点的行、列
// 遍历四个方向
for (int i = 0; i < 4; i++) {
// 计算新坐标(a=新行,b=新列)
int a = x + dx[i], b = y + dy[i];
// 合法性判断:
// 1. 坐标在矩阵范围内(1≤a≤n,1≤b≤m);
// 2. 未访问过(dist[a][b]==-1);
if (a >= 1 && a <= n && b >= 1 && b <= m && dist[a][b] == -1) {
dist[a][b] = dist[x][y] + 1; // 新点距离=当前点距离+1
q.push({a, b}); // 新点入队,继续扩展
}
}
}
}
int main() {
// 第一步:输入矩阵尺寸和01矩阵
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j]; // 输入每个位置的字符(0或1)
}
}
// 第二步:执行多源BFS,计算所有点的最短距离
bfs();
// 第三步:输出距离矩阵(每行的数用空格分隔)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << dist[i][j] << " "; // 输出当前位置的距离
}
cout << endl; // 每行结束换行
}
return 0;
}2.2.2 刺杀⼤使
题⽬来源: 洛⾕
题⽬链接: P1902 刺杀⼤使
难度系数: ★★★
题目描述
某组织正在策划一起对某大使的刺杀行动。他们来到了使馆,准备完成此次刺杀,要进入使馆首先必须通过使馆前的防御迷阵。
迷阵由 n×m 个相同的小房间组成,每个房间与相邻四个房间之间有门可通行。在第 n 行的 m 个房间里有 m 个机关,这些机关必须全部打开才可以进入大使馆。而第 1 行的 m 个房间有 m 扇向外打开的门,是迷阵的入口。除了第 1 行和第 n 行的房间外,每个房间都被使馆的安保人员安装了激光杀伤装置,将会对进入房间的人造成一定的伤害。第 i 行第 j 列 造成的伤害值为 pi,j(第 1 行和第 n 行的 p 值全部为 0)。
现在某组织打算以最小伤害代价进入迷阵,打开全部机关,显然,他们可以选择任意多的人从任意的门进入,但必须到达第 n 行的每个房间。一个士兵受到的伤害值为他到达某个机关的路径上所有房间的伤害值中的最大值,整个部队受到的伤害值为所有士兵的伤害值中的最大值。现在,这个恐怖组织掌握了迷阵的情况,他们需要提前知道怎么安排士兵的行进路线可以使得整个部队的伤害值最小。
输入格式
第一行有两个整数 n,m,表示迷阵的大小。
接下来 n 行,每行 m 个数,第 i 行第 j 列的数表示 pi,j。
输出格式
输出一个数,表示最小伤害代价。
输入输出样例
输入 #1复制
4 2
0 0
3 5
2 4
0 0 输出 #1复制
3说明/提示
- 50% 的数据,n,m≤100;
- 100% 的数据,n,m≤1000,pi,j≤1000。
【解法】
直接找答案显然是不现实的,因为能⾛的路径实在是太多了,如果全都枚举出来时间上吃不消。但是 题⽬要求的是最⼤值最⼩化,可以 尝试⽤⼆分来优化枚举 。
设最终结果是 x ,会发现⼀个性质:
• 当规定搜索过程中的最⼤值⼤于等于 x 时 ,我们**⼀定可以从第⼀⾏⾛到最后⼀⾏;
• 当规定搜索过程中的最⼤值⼩于** x 时 ,我们**⼀定不能⾛到最后⼀⾏**。
因此,我们可以 ⼆分最终结果 ,通过 bfs 或者 dfs 来 判断是否能⾛到最后⼀⾏ 。
如果⽤dfs ,那就从第⼀⾏的每⼀列开始,全都搜索⼀遍。如果⽤ bfs,可以看成多源bfs 问题,
直接把所有的源点加⼊队列中,然后正常搜索即可。
【参考代码】
cpp
#include <iostream>
#include <cstring> // memset初始化数组
#include <queue> // BFS队列
using namespace std;
const int N = 1010; // 矩阵最大尺寸(n/m≤1000,1010足够)
int n, m; // 迷阵的行数n,列数m
int p[N][N]; // 每个房间的伤害值(第1/n行全为0)
bool st[N][N]; // 标记数组:st[i][j]=true表示该房间已访问,避免重复走
// 方向数组:上下左右四个方向(行偏移dx,列偏移dy)
int dx[4] = {0, 0, 1, -1}; // 0=右,0=左,1=下,-1=上
int dy[4] = {1, -1, 0, 0}; // 1=右,-1=左,0=下,0=上
// BFS函数:判断"路径最大伤害≤mid"时,能否从第1行走到第n行
bool bfs(int mid) {
memset(st, 0, sizeof st); // 每次BFS重置标记数组(未访问)
queue<pair<int, int>> q; // BFS队列,存储待扩展的坐标
// 多源初始化:第1行所有房间都是入口,全部加入队列
for (int j = 1; j <= m; j++) {
q.push({1, j}); // 第1行第j列入队
st[1][j] = true; // 标记为已访问
}
while (q.size()) { // 队列不为空时持续扩展
auto [a, b] = q.front(); // 取出队首坐标(当前房间)
q.pop(); // 从队列中删除
// 终止条件:只要到达第n行(机关行),直接返回true(能到达)
if (a == n) return true;
// 遍历四个方向
for (int i = 0; i < 4; i++) {
// 计算新坐标(x=新行,y=新列)
int x = a + dx[i], y = b + dy[i];
// 合法性判断:
// 1. 坐标在迷阵范围内(1≤x≤n,1≤y≤m);
// 2. 未访问过(st[x][y]=false);
if (x >= 1 && x <= n && y >= 1 && y <= m && !st[x][y]) {
// 剪枝:如果新房间的伤害值>mid,路径最大伤害会超过mid,跳过
if (p[x][y] > mid) continue;
st[x][y] = true; // 标记为已访问
q.push({x, y}); // 新房间入队,继续扩展
}
}
}
// 遍历完所有可达房间,仍未到达第n行,返回false
return false;
}
int main() {
cin >> n >> m;
int l = 0, r = 0; // 二分的左右边界:l=0,r=矩阵最大伤害值
// 输入迷阵的伤害值,并确定二分右边界r
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> p[i][j];
r = max(r, p[i][j]); // r更新为当前最大的伤害值
}
}
// 二分查找:找最小的mid,使得bfs(mid)=true
while (l < r) {
int mid = (l + r) >> 1; // 等价于(l+r)/2,位运算更快
if (bfs(mid)) { // 如果mid可行(能到达第n行)
r = mid; // 尝试找更小的mid,缩小右边界
} else { // 如果mid不可行
l = mid + 1; // 必须增大mid,缩小左边界
}
}
// 最终l=r,就是最小的最大伤害值
cout << l << endl;
return 0;
}2.3 01 BFS
2.3.1 ⼩明的游戏
题⽬来源: 洛⾕
题⽬链接: P4554 ⼩明的游戏
难度系数: ★★
题目描述
小明最近喜欢玩一个游戏。给定一个 n×m 的棋盘,上面有两种格子 # 和 @。游戏的规则很简单:给定一个起始位置和一个目标位置,小明每一步能向上,下,左,右四个方向移动一格。如果移动到同一类型的格子,则费用是 0,否则费用是 1。请编程计算从起始位置移动到目标位置的最小花费。
输入格式
输入文件有多组数据。
输入第一行包含两个整数 n,m,分别表示棋盘的行数和列数。
输入接下来的 n 行,每一行有 m 个格子(使用 # 或者 @ 表示)。
输入接下来一行有四个整数 x1,y1,x2,y2,分别为起始位置和目标位置。
当输入 n,m 均为 0 时,表示输入结束。
输出格式
对于每组数据,输出从起始位置到目标位置的最小花费。每一组数据独占一行。
输入输出样例
输入 #1复制
2 2
@#
#@
0 0 1 1
2 2
@@
@#
0 1 1 0
0 0输出 #1复制
2
0说明/提示
对于20%的数据满足:1≤n,m≤10。
对于40%的数据满足:1≤n,m≤300。
对于100%的数据满足:1≤n,m≤500。
【解法】
01bfs模板题。
• 如果⾛到相同格⼦,权值为 0 ,更新最短距离,然后加⼊到队头;
• 如果⾛到不同格⼦,权值为 1 ,更新最短距离,然后加⼊到队尾。
其余的搜索⽅式与常规 bfs⼀模⼀样。
【参考代码】
cpp
#include <iostream>
#include <deque> // 双端队列(01-BFS核心,支持队头/队尾插入)
#include <cstring> // memset初始化距离数组
using namespace std;
const int N = 510; // 棋盘最大尺寸(n/m≤500,510足够)
int n, m, x1, y1, x2, y2; // 棋盘尺寸、起点/终点坐标
char g[N][N]; // 存储棋盘(#/@)
int dist[N][N]; // 距离数组:dist[i][j] = 起点到(i,j)的最小花费,-1表示未访问
// 方向数组:上下左右四个方向(行偏移dx,列偏移dy)
int dx[4] = {0, 0, 1, -1}; // 0=右,0=左,1=下,-1=上
int dy[4] = {1, -1, 0, 0}; // 1=右,-1=左,0=下,0=上
int bfs() {
// 特判:起点就是终点,花费为0
if (x1 == x2 && y1 == y2) return 0;
// 初始化距离数组:所有值设为-1(未访问)
memset(dist, -1, sizeof dist);
// 双端队列q:存储待扩展的坐标(pair<int,int>)
deque<pair<int, int>> q;
// 起点入队(队尾,也可以队头,不影响)
q.push_back({x1, y1});
dist[x1][y1] = 0; // 起点花费为0
while (q.size()) { // 队列不为空时持续扩展
// 取出队首坐标(01-BFS必须从队首取,保证优先处理边权0的节点)
auto [a, b] = q.front();
q.pop_front();
// 遍历四个方向
for (int i = 0; i < 4; i++) {
// 计算新坐标(x=新行,y=新列)
int x = a + dx[i], y = b + dy[i];
// 合法性判断:
// 1. 坐标在棋盘范围内(1≤x≤n,1≤y≤m);
// 2. 未访问过(dist[x][y]==-1);
if (x >= 1 && x <= n && y >= 1 && y <= m && dist[x][y] == -1) {
// 当前格子类型(prev)和新格子类型(cur)
char prev = g[a][b], cur = g[x][y];
if (prev == cur) { // 类型相同,边权0
dist[x][y] = dist[a][b]; // 花费不变
q.push_front({x, y}); // 加入队头(优先处理)
} else { // 类型不同,边权1
dist[x][y] = dist[a][b] + 1; // 花费+1
q.push_back({x, y}); // 加入队尾(常规处理)
}
// 终止条件:到达终点,直接返回花费(01-BFS第一次到达就是最小值)
if (x == x2 && y == y2) return dist[x2][y2];
}
}
}
return -1; // 理论上不会执行(题目保证有路径)
}
int main() {
// 多组输入:直到n和m都为0时结束
while (cin >> n >> m) {
if (!n && !m) break; // 终止条件
// 输入棋盘(注意:代码中棋盘坐标从1开始,输入是0开始)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
// 输入起点(x1,y1)和终点(x2,y2)(输入是0-based,转换为1-based)
cin >> x1 >> y1 >> x2 >> y2;
x1++, y1++, x2++, y2++; // 0→1,比如输入0 0 → 1 1
// 执行BFS,输出最小花费
cout << bfs() << endl;
}
return 0;
}2.3.2 Three States
题⽬来源: 洛⾕
题⽬链接: Three States
难度系数: ★★★★
题目描述
著名的全球经济危机正在迅速逼近,因此伯曼、伯兰斯和伯塔利三个州组建了一个联盟,并允许所有成员国的居民自由通过任意一个成员国的领土。此外,决定在各州之间修建道路,以保证可以从任何一个国家的任意地点到达其他国家的任意地点。
由于修路总是昂贵的,新成立联盟的各国政府请你帮忙评估成本。为此,你被发放了一张地图,地图可以表示为一个包含 n 行 m 列的矩形表格。地图上的每个格子要么属于三个州中的某一个州,要么是允许修建道路的区域(用 "." 表示),要么是禁止修建道路的区域(用 "#" 表示)。如果一个格子属于某个州,或者在该格子上修建了道路,则称该格子为"可通行"的。你可以从任意一个可通行格子向上、下、左、右移动一格,如果移动到的格子存在且可通行。
你的任务是在尽量少的格子内修建道路,使得能够通过仅经过可通行格子,从任何一个国家的任意格子到达其他国家的任意格子。
保证初始时,每个国家内部的任意两个格子可以互相到达(仅通过本国格子的移动)。保证每个国家至少有一个格子属于它。
输入格式
输入的第一行包含地图的尺寸 n 和 m(1≤n,m≤1000),分别表示行数和列数。
接下来的 n 行每行包含 m 个字符,描述地图的各行。字符 1 到 3 表示该格子属于相应的国家。字符 "." 表示该格子允许修路,字符 "#" 表示该格子禁止修路。
输出格式
输出一个整数,表示需要修路的最小格子数,使得所有国家的所有格子互相连通。如果无法实现,输出 −1。
显示翻译
题意翻译
输入输出样例
输入 #1复制
4 5
11..2
#..22
#.323
.#333输出 #1复制
2输入 #2复制
1 5
1#2#3输出 #2复制
-1说明/提示
由 ChatGPT 5 翻译
【解法】
正难则反: • 直接找出结果点是很⿇烦的,需要枚举所有的点,然后每个点都要来⼀次 bfs ,这样是会超时的。
• 可以依次从三个国家出发,⽤ bfs计算出来到达所有点的最短距离 。求出所有距离之后,重新遍
历所有的点,分情况求出到三个国家的最短距离。
算法原理很简单,但是⾥⾯有很多细节需要注意:
- 因为每个国家可能有很多点,并且国家的点与点之间不连通,因此我们要⽤ 多源 bfs 求某个国家
到所有点的最短距离; - 国家与国家之间的点如果相连,它们之间的距离是 0(⽆论是不是同⼀个国家,在我们这道题⾥
⾯,它们的距离都是0 ,因为都不需要修路)。那么我们这道题⾥⾯边的权值要么是0 ,要么是
1。因此需要⽤01bfs 来更新所有的距离; - 计算某⼀个点到三个国家的最短距离时,应该分情况讨论。设 分别表⽰三个国家到该点的
最短距离:
a , b , c
a. 如果该点是⼀个国家,最短距离为 a + b + c;
b. 如果该点是⼀个荒地,最短距离为a+b+c-2 ,因为我们计算最短距离的时候,荒地会被
计算三次,所以要减去两次
【参考代码】
cpp
#include <iostream>
#include <deque> // 双端队列(01-BFS核心)
#include <cstring> // memset初始化距离数组
using namespace std;
const int N = 1e3 + 10; // 地图最大尺寸(n,m≤1e3)
int n, m; // 地图行数、列数
char g[N][N]; // 存储地图(. / # / 1/2/3)
// dist[num][x][y]:国家num(1/2/3)到(x,y)的最少修路数,-1表示不可达
int dist[4][N][N];
// 方向数组:上下左右四个方向(行偏移dx,列偏移dy)
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
// 多源01-BFS:计算国家num到所有点的最少修路数
void bfs(int num) {
// 初始化:当前国家的距离数组全设为-1(不可达)
memset(dist[num], -1, sizeof dist[num]);
deque<pair<int, int>> q; // 双端队列(01-BFS)
// 多源初始化:把国家num的所有格子加入队列(起点)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 找到当前国家的所有格子(比如num=1时,g[i][j]='1')
if (g[i][j] - '0' == num) {
q.push_back({i, j}); // 入队
dist[num][i][j] = 0; // 国家格子到自己的修路数为0
}
}
}
// 01-BFS核心逻辑
while (q.size()) {
// 取出队首节点(优先处理边权0的节点)
auto [a, b] = q.front();
q.pop_front();
// 遍历四个方向
for (int i = 0; i < 4; i++) {
int x = a + dx[i], y = b + dy[i]; // 新坐标
// 合法性判断:坐标在地图范围内(1≤x≤n,1≤y≤m)
if (x >= 1 && x <= n && y >= 1 && y <= m) {
// 剪枝:石头(#)或已访问过(dist[num][x][y]≠-1),跳过
if (g[x][y] == '#' || dist[num][x][y] != -1) continue;
if (g[x][y] == '.') { // 荒地:边权1(需要修路)
dist[num][x][y] = dist[num][a][b] + 1; // 修路数+1
q.push_back({x, y}); // 加入队尾
} else { // 国家格子(1/2/3):边权0(无需修路)
dist[num][x][y] = dist[num][a][b]; // 修路数不变
q.push_front({x, y}); // 加入队头(优先处理)
}
}
}
}
}
int main() {
// 输入地图尺寸和地图内容(1-based坐标)
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
// 分别计算国家1、2、3到所有点的最少修路数
bfs(1);
bfs(2);
bfs(3);
int ret = 1e6 + 10; // 初始化答案为极大值(表示无解)
// 遍历所有点,找最小总修路数
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 取出当前点到三个国家的修路数
int a = dist[1][i][j], b = dist[2][i][j], c = dist[3][i][j];
// 剪枝:任意一个国家不可达,跳过该点
if (a == -1 || b == -1 || c == -1) continue;
// 计算该点作为枢纽的总修路数
if (g[i][j] == '.') { // 荒地:总修路数=a+b+c-2
ret = min(ret, a + b + c - 2);
} else { // 国家格子:总修路数=a+b+c
ret = min(ret, a + b + c);
}
}
}
// 输出结果:若ret仍为极大值,无解输出-1;否则输出最小值
if (ret == 1e6 + 10) {
cout << -1 << endl;
} else {
cout << ret << endl;
}
return 0;
}3. Floodfill 问题
3.1 Lake Counting
题⽬来源: 洛⾕
题⽬链接: P1596 [USACO10OCT] Lake Counting S
难度系数: ★★
题目描述
由于最近的降雨,水在农夫约翰的田地里积聚了。田地可以表示为一个 N×M 的矩形(1≤N≤100;1≤M≤100)。每个方格中要么是水(W),要么是干地(.)。农夫约翰想要弄清楚他的田地里形成了多少个水塘。一个水塘是由连通的水方格组成的,其中一个方格被认为与它的八个邻居相邻。给定农夫约翰田地的示意图,确定他有多少个水塘。
输入格式
第 1 行:两个用空格分隔的整数:N 和 M。
第 2 行到第 N+1 行:每行 M 个字符,表示农夫约翰田地的一行。
每个字符要么是 W,要么是 .。
字符之间没有空格。
输出格式
第 1 行:农夫约翰田地中的水塘数量。
显示翻译
题意翻译
输入输出样例
输入 #1复制
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.输出 #1复制
3说明/提示
输出详情:共有三个水塘:一个在左上角,一个在左下角,还有一个沿着右侧。
(由 ChatGPT 4o 翻译)
【解法】
遍历整个矩阵,当遇到⼀个没有标记过的⽔坑时:
• 计数;
• 然后⽤ bfs或者 dfs将整个湖全都标记⼀下。
整个矩阵遍历⼀遍,就能得出湖的数量
【参考代码】
cpp
#include <iostream>
#include <queue> // BFS需要的队列
#include <cstring> // 可选:memset初始化标记数组
using namespace std;
const int N = 110; // 网格最大尺寸(100+10,避免边界越界)
int n, m; // 网格的行数、列数
char g[N][N]; // 存储网格(W/.)
bool st[N][N]; // 标记数组:st[i][j]=true表示该位置已访问(避免重复处理)
// 8个方向的偏移量(上下左右 + 四个对角线)
int dx[8] = {0, 0, 1, -1, 1, 1, -1, -1};
int dy[8] = {1, -1, 0, 0, 1, -1, 1, -1};
// BFS:把(i,j)所在的整个水坑标记为已访问
void bfs(int i, int j) {
queue<pair<int, int>> q; // 队列存储待处理的坐标
q.push({i, j}); // 起点入队
st[i][j] = true; // 标记为已访问
while (q.size()) { // 队列不为空时循环
// 取出队首坐标(C++17结构化绑定,兼容写法见下文)
auto [a, b] = q.front();
q.pop_front(); // 弹出队首
// 遍历8个方向
for (int k = 0; k < 8; k++) {
int x = a + dx[k]; // 新行坐标
int y = b + dy[k]; // 新列坐标
// 边界判断:坐标超出网格范围 → 跳过
if (x < 1 || x > n || y < 1 || y > m) continue;
// 跳过条件:已访问 或 不是水(是旱地)→ 跳过
if (st[x][y] || g[x][y] == '.') continue;
st[x][y] = true; // 标记为已访问
q.push({x, y}); // 新坐标入队,继续扩展
}
}
}
// DFS:递归版,逻辑和BFS完全一致(把队列换成递归栈)
void dfs(int i, int j) {
st[i][j] = true; // 标记当前位置为已访问
// 遍历8个方向
for (int k = 0; k < 8; k++) {
int x = i + dx[k];
int y = j + dy[k];
// 边界+已访问+非水 → 跳过
if (x < 1 || x > n || y < 1 || y > m) continue;
if (st[x][y] || g[x][y] == '.') continue;
dfs(x, y); // 递归处理下一个位置
}
}
int main() {
// 输入网格尺寸
cin >> n >> m;
// 输入网格内容(1-based坐标,避免x=0/y=0的边界问题)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
int ret = 0; // 水坑计数,初始为0
// 遍历网格每一个位置
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 找到未访问的W → 新水坑
if (g[i][j] == 'W' && !st[i][j]) {
ret++; // 计数+1
// bfs(i, j); // 选BFS或DFS都可以,二选一
dfs(i, j); // 标记该水坑的所有连通W为已访问
}
}
}
// 输出水坑总数
cout << ret << endl;
return 0;
}3.2 填涂颜⾊
题⽬来源: 洛⾕
题⽬链接: P1162 填涂颜⾊
难度系数: ★★
题目描述
由数字 0 组成的方阵中,有一任意形状的由数字 1 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 2。例如:6×6 的方阵(n=6),涂色前和涂色后的方阵如下:
如果从某个 0 出发,只向上下左右 4 个方向移动且仅经过其他 0 的情况下,无法到达方阵的边界,就认为这个 0 在闭合圈内 。闭合圈不一定是环形的,可以是任意形状,但保证闭合圈内的 0 是连通的(两两之间可以相互到达)。
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1输入格式
每组测试数据第一行一个整数 n(1≤n≤30)。
接下来 n 行,由 0 和 1 组成的 n×n 的方阵。
方阵内只有一个闭合圈,圈内至少有一个 0。
输出格式
已经填好数字 2 的完整方阵。
输入输出样例
输入 #1复制
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1输出 #1复制
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1说明/提示
对于 100% 的数据,1≤n≤30。
【解法】
正难则反:直接找出被 1包围的 0是很困难的,因为很难确定当前搜索到的这个0 是否是被包围
的。但是,我们如果从边缘的 0开始搜索,搜索到的 0⼀定是没有被包围的。
因此,我们可以从边缘的 0开始搜索,标记所有与边缘0 相连的联通块。那么,没有被标记过的0
就是被包围的。
⼩技巧:
• 我们可以把整个矩阵的外围包上⼀层 ,这样只⽤从【0,0】 位置开始搜即可。不⽤遍历第⼀⾏第 ⼀列,最后⼀⾏以及最后⼀列
【参考代码】
cpp
#include <iostream>
#include <queue>
using namespace std;
const int N = 35; // 方阵最大尺寸(30+5)
int n; // 原方阵大小n×n
int g[N][N]; // 存储方阵(外围包一圈0,坐标0~n+1)
bool st[N][N]; // 标记数组:st[i][j]=true表示能到达边缘的0
// 4个方向偏移量
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void bfs(int i, int j) {
queue<pair<int, int>> q;
q.push({i, j});
st[i][j] = true;
while (q.size()) {
auto t = q.front();
q.pop();
int a = t.first, b = t.second;
// 遍历4个方向
for (int k = 0; k < 4; k++) {
int x = a + dx[k], y = b + dy[k];
// 边界判断:0 ≤ x ≤ n+1,0 ≤ y ≤ n+1(包含外围的0)
// 跳过条件:是1 或 已标记 → 只处理未标记的0
if (x >= 0 && x <= n + 1 && y >= 0 && y <= n + 1 && g[x][y] == 0 && !st[x][y]) {
st[x][y] = true;
q.push({x, y});
}
}
}
}
int main() {
cin >> n;
// 输入原方阵(存储在1~n行,1~n列)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> g[i][j];
}
}
// 关键:从外围的(0,0)开始BFS,自动标记所有能到达边缘的0
bfs(0, 0);
// 输出最终方阵(仅输出1~n行,1~n列)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (g[i][j] == 1) { // 是1 → 输出1
cout << g[i][j] << " ";
} else if (st[i][j]) { // 是0且能到达边缘 → 输出0
cout << 0 << " ";
} else { // 是0且闭合圈内 → 输出2
cout << 2 << " ";
}
}
cout << endl;
}
return 0;
}