计算机图形学：【Games101】学习笔记04——着色（光照与基本着色模型，着色频率、图形管线、纹理映射）

计算机图形学：【Games101】学习笔记04------着色（光照与基本着色模型，着色频率、图形管线、纹理映射）

前言
一、着色（光照与基本着色模型）
- [1.1 Visibility 处理：解决物体遮挡问题（Visibility / occlusion）](#1.1 Visibility 处理：解决物体遮挡问题（Visibility / occlusion）)
- - [1.1.1 画家算法（Painter's Algorithm）](#1.1.1 画家算法（Painter’s Algorithm）)
  - [1.1.2 Z 缓冲算法（Z-Buffer）](#1.1.2 Z 缓冲算法（Z-Buffer）)
- [1.2 着色（Shading）基础：给物体添加光影](#1.2 着色（Shading）基础：给物体添加光影)
- - [1.2.1 着色的基本概念](#1.2.1 着色的基本概念)
  - [1.2.2 简单的着色模型（Blinn-Phong 反射模型）](#1.2.2 简单的着色模型（Blinn-Phong 反射模型）)
二、着色（着色频率、图形管线、纹理映射）
- [2.1 Blinn-Phong 反射模型进阶](#2.1 Blinn-Phong 反射模型进阶)
- - [2.1.1 漫反射项（Lambertian Term）](#2.1.1 漫反射项（Lambertian Term）)
  - [2.1.2 高光项（Specular Term）](#2.1.2 高光项（Specular Term）)
  - [2.1.3 环境光项（Ambient Term）](#2.1.3 环境光项（Ambient Term）)
  - [2.1.4 完整Blinn-Phong 反射模型（Blinn-Phong Reflection Model）](#2.1.4 完整Blinn-Phong 反射模型（Blinn-Phong Reflection Model）)
- [2.2 着色频率（Shading Frequencies）](#2.2 着色频率（Shading Frequencies）)
- - [2.2.1 平面着色（Shade each triangle (flat shading)）](#2.2.1 平面着色（Shade each triangle (flat shading)）)
  - [2.2.2 Gouraud着色（Shade each vertex (Gouraud shading)）](#2.2.2 Gouraud着色（Shade each vertex (Gouraud shading)）)
  - [2.2.3 Phong 着色（Shade each pixel (Phong shading)）](#2.2.3 Phong 着色（Shade each pixel (Phong shading)）)
  - [2.2.4 三种着色方法的对比](#2.2.4 三种着色方法的对比)
  - [2.2.5 补充：定义每个顶点的法向量（Defining Per-Vertex Normal Vectors）](#2.2.5 补充：定义每个顶点的法向量（Defining Per-Vertex Normal Vectors）)
- [2.3 实时渲染管线（Graphics Pipeline）](#2.3 实时渲染管线（Graphics Pipeline）)
- - [2.3.1 管线各核心阶段](#2.3.1 管线各核心阶段)
  - [2.3.2 着色器（Shader Programs）](#2.3.2 着色器（Shader Programs）)
  - [2.3.3 GPU 架构与并行计算（Graphics Pipeline Implementation: GPUs）](#2.3.3 GPU 架构与并行计算（Graphics Pipeline Implementation: GPUs）)
- [2.4 纹理映射（Texture Mapping）](#2.4 纹理映射（Texture Mapping）)
三、疑难点整理总结
写在最后

前言

🎮 GAMES101 是国内相当有名的图形学公开课。项目相关资源在：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html。

本 📒笔记为 🖊️笔者在自学过程中整理的 🇨🇳中文版笔记，供各位 📖读者阅读 😼～

计算机图形学中， visibility 处理与着色是实现真实渲染的核心环节。GAMES101 第 7 讲围绕 Z 缓冲算法、着色模型及图形管线展开，清晰拆解了从物体遮挡判断到表面光影呈现的关键技术，本文将梳理核心知识点与实践要点。

一、着色（光照与基本着色模型）

1.1 Visibility 处理：解决物体遮挡问题（Visibility / occlusion）

在 3D 场景渲染中，多个物体重叠时需确定哪些部分可见，这一问题的核心是遮挡判断。

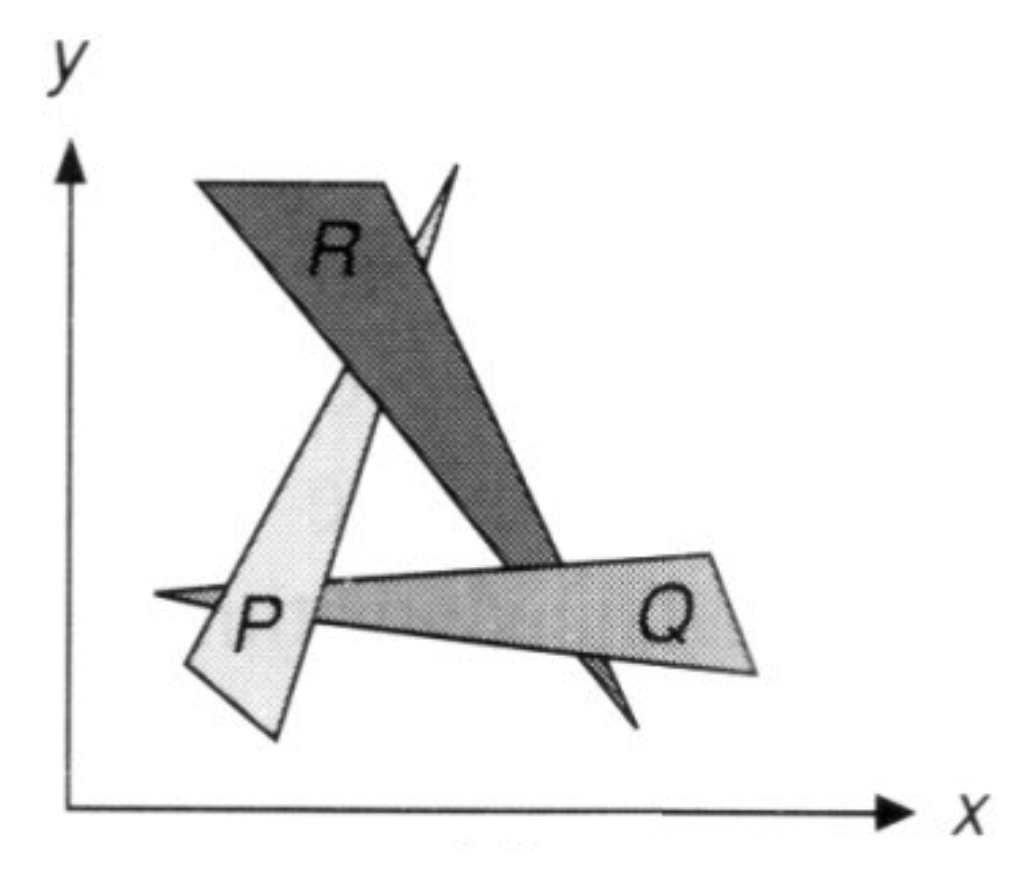
1.1.1 画家算法（Painter's Algorithm）

核心思路：模拟绘画逻辑，按深度从后往前绘制，用前景物体颜色覆盖后景物体。

特点：需对所有三角形进行深度排序，时间复杂度为 O (n logn)（n 为三角形数量）。

问题：存在明显缺陷，部分场景下无法确定深度顺序，导致遮挡判断失效。

1.1.2 Z 缓冲算法（Z-Buffer）

这是目前 GPU 硬件普遍采用的 visibility 解决方案，也是本讲重点。

核心原理 ：

维护两个缓冲区：帧缓冲区（framebuffer）存储像素颜色，深度缓冲区（z-buffer）存储每个像素的当前最小 z 值。

约定 z 值为正数，且 z 值越小表示物体越靠近相机，z 值越大表示物体越远。

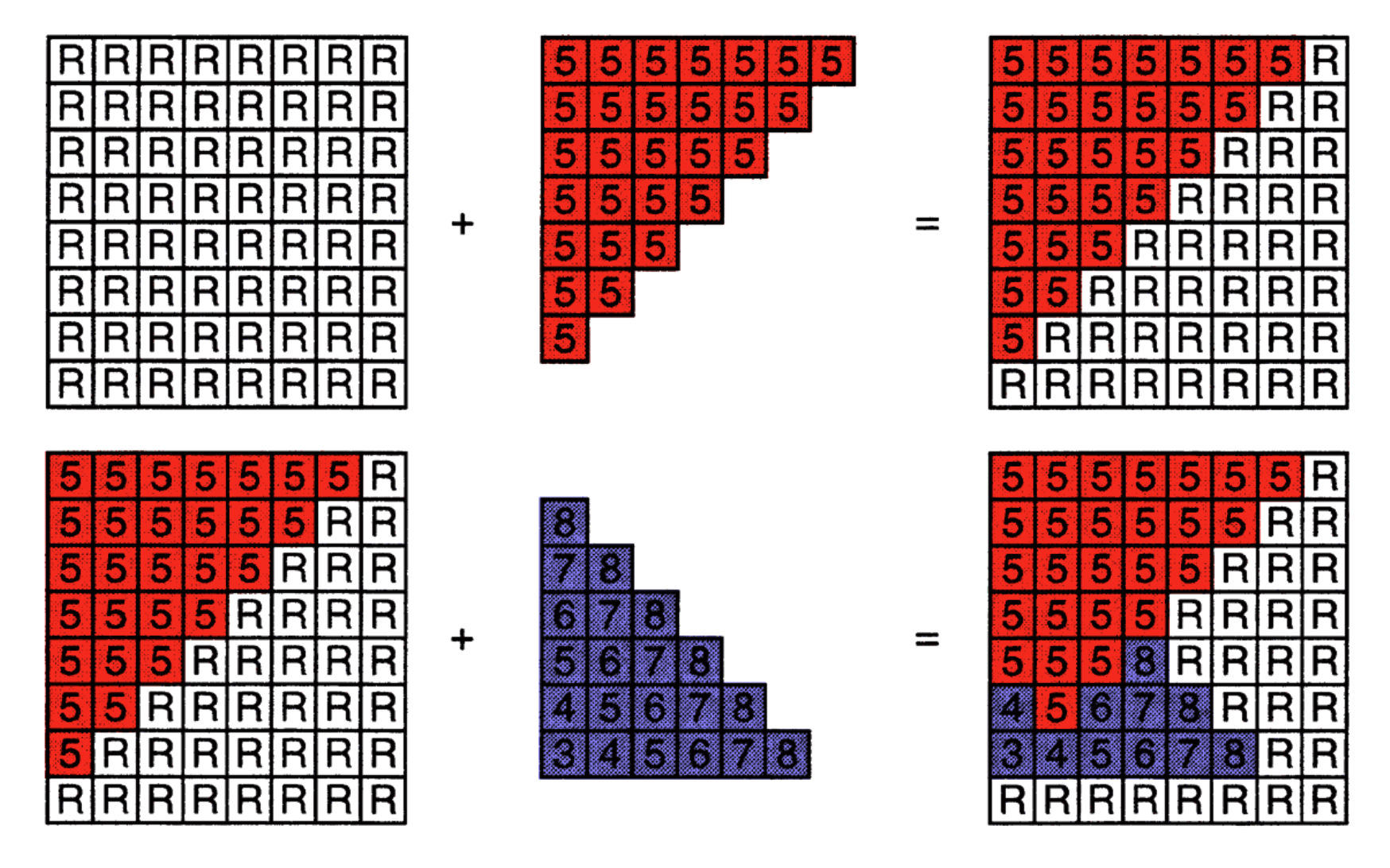
算法步骤 ：

初始化深度缓冲区所有值为无穷大（∞）。

光栅化每个三角形时，遍历其覆盖的每个采样点（x, y, z）。

若当前采样点的 z 值小于深度缓冲区中对应位置的 z 值，说明该点更靠近相机。

更新帧缓冲区对应位置的颜色，并将深度缓冲区的 z 值更新为当前采样点的 z 值。

若 z 值不小于缓冲区中的值，则该采样点被遮挡，不做任何操作。

关键优势:

时间复杂度为 O (n)（假设每个三角形覆盖的采样点数量固定），无需提前排序。

不受物体绘制顺序影响，能处理复杂遮挡场景。

硬件级实现，渲染效率极高，是现代图形学中最核心的 visibility 算法。

1.2 着色（Shading）基础：给物体添加光影

解决遮挡问题后，需通过着色让物体呈现材质质感与光影效果，本讲重点介绍 Blinn-Phong 反射模型。

1.2.1 着色的基本概念

1. 着色的定义

词典定义：用平行线或色块对插图、图表进行暗化或上色的过程。

课程定义：将材质属性应用于物体表面的过程，核心是计算特定点向相机反射的光强。

2. 着色的核心特性

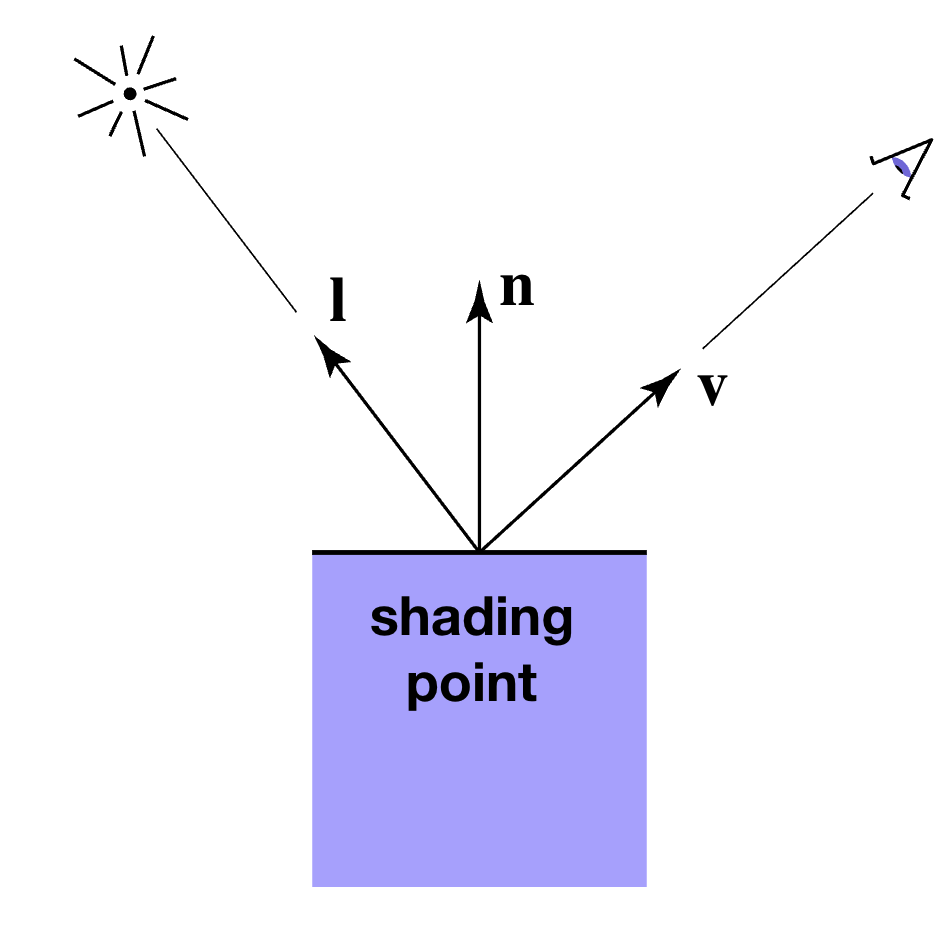
局部性：仅基于着色点的局部信息计算（观察者方向、表面法向量、光线方向等）。

与阴影的区别：着色不包含阴影计算，仅处理物体表面自身的光影反射。

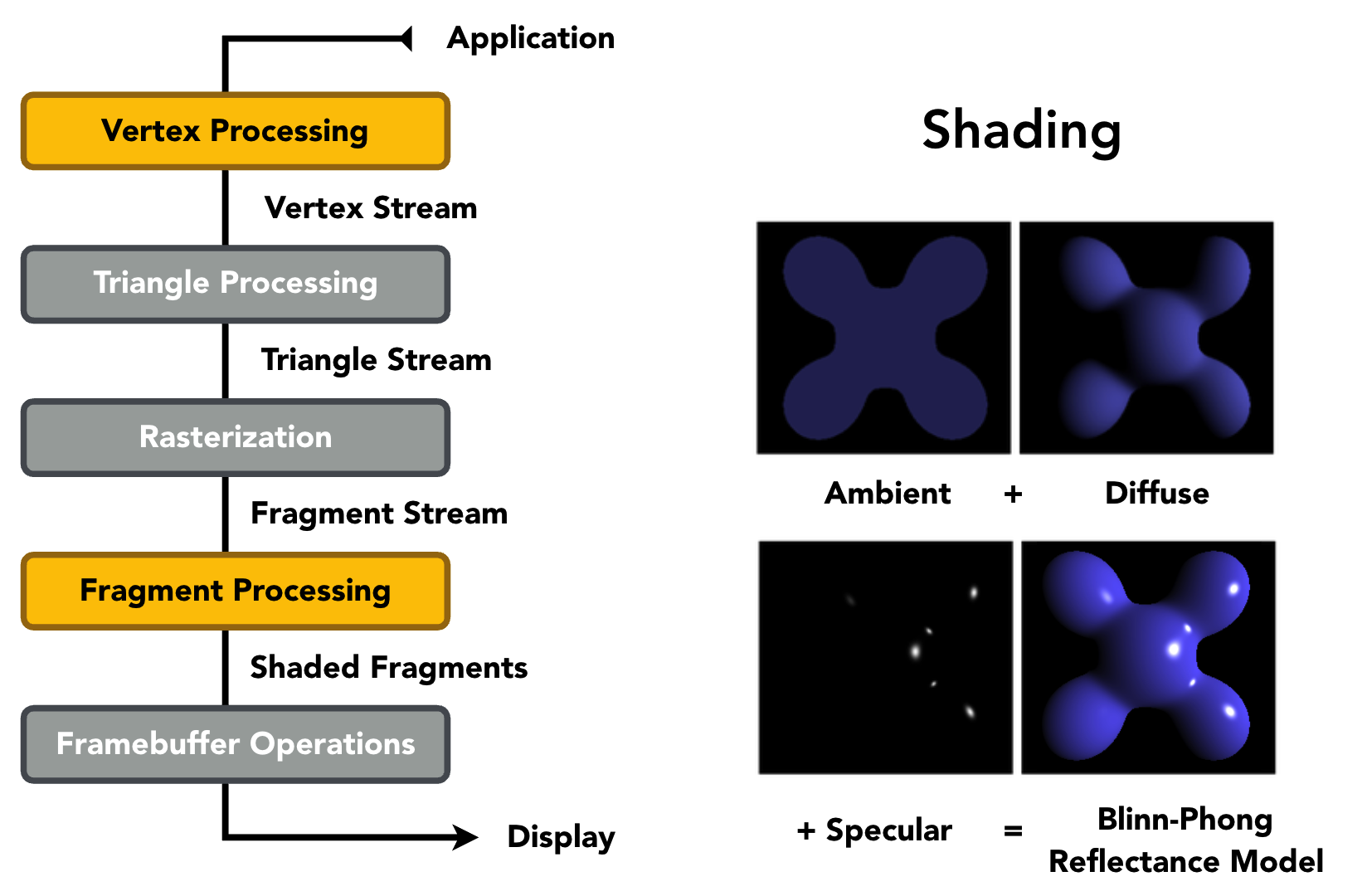
1.2.2 简单的着色模型（Blinn-Phong 反射模型）

Blinn-Phong 反射模型通过叠加三种光照效果，实现符合人眼感知的着色效果：

1.漫反射（Diffuse Reflection）

光线照射到粗糙表面后，向各个方向均匀散射，物体颜色在所有视角下保持一致。

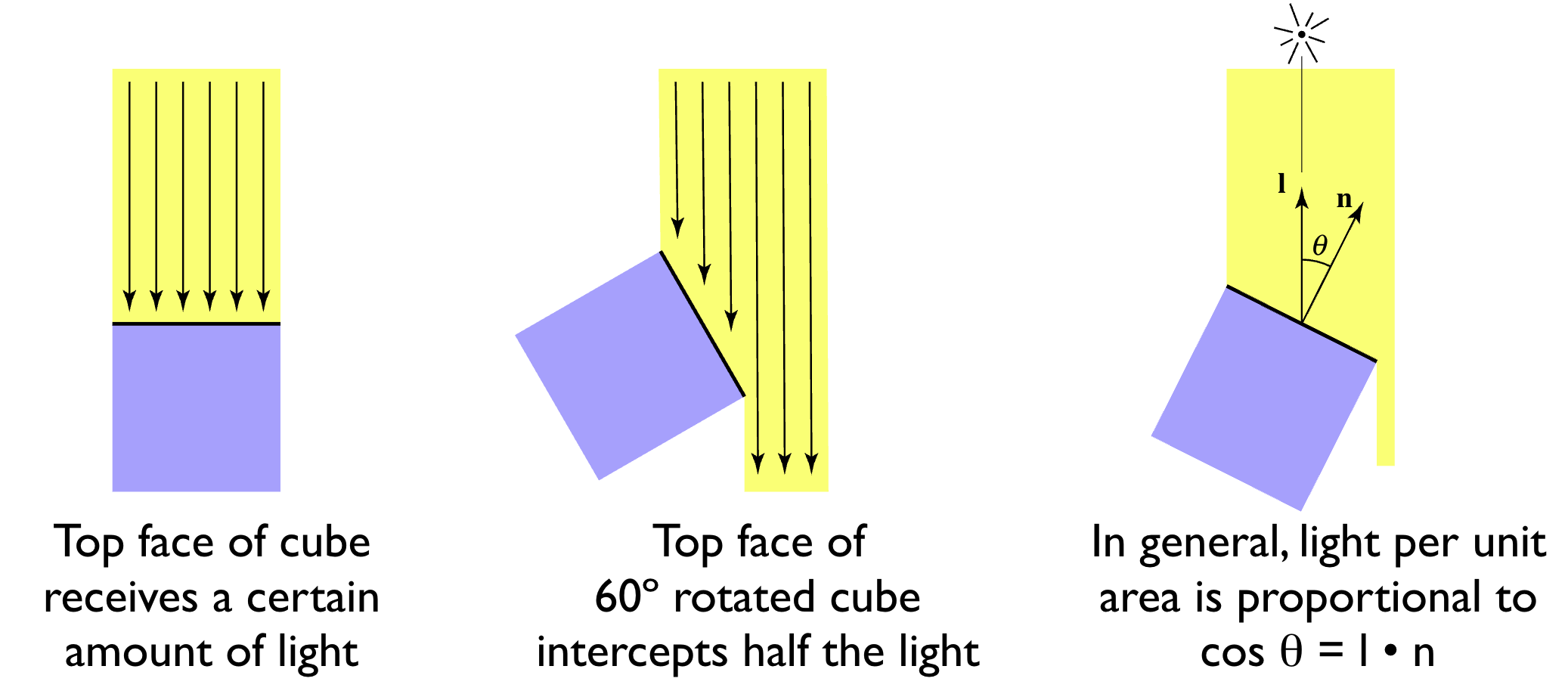
遵循朗伯余弦定律( Lambert's cosine law )：单位面积接收的光能量与光线方向和表面法向量的夹角余弦成正比，即 cosθ = n・l（n 为单位法向量，l 为单位光线方向）。

计算公式：Ld = kd × (I/r²) × max (0, n・l)

kd 为漫反射系数（决定物体基础颜色）。

I 为光源强度，r 为着色点到光源的距离。

max (0, n・l) 确保光线从物体正面照射时才计算贡献（避免负光强）。

2.高光反射（Specular Highlights）

光线照射到光滑表面后，在特定方向形成明亮的高光区域，与观察角度相关。

3.环境光（Ambient Lighting）

模拟场景中四处反射的间接光，避免未被直接光照的区域呈现纯黑色，提升画面整体亮度。

4.光线衰减（Light Falloff）

点光源的光强会随距离增加而衰减，遵循平方反比定律，即光强与距离的平方成反比（I/r²）。

这一特性确保远处物体看起来更暗，符合真实物理规律。

二、着色（着色频率、图形管线、纹理映射）

在计算机图形学中，着色（Shading）是实现真实感画面的核心技术之一。GAMES101 第八讲作为光照模型的进阶内容，不仅深入完善了 Blinn-Phong 反射模型，还系统讲解了着色频率、实时渲染管线、纹理映射等关键技术，这些内容共同构成了现代实时图形渲染的基础框架。本文将结合课程知识点，梳理核心概念与技术细节，帮助读者建立完整的渲染知识体系。

2.1 Blinn-Phong 反射模型进阶

上一讲我们初步了解了 Blinn-Phong 模型的核心思想，本讲进一步完善了模型细节，并明确了三个核心分量的数学表达与物理意义，最终形成完整的光照计算框架。

2.1.1 漫反射项（Lambertian Term）

漫反射的特点是光线照射到粗糙表面后，会向各个方向均匀散射，因此其亮度与观察方向无关，仅取决于入射光线与表面法向量的夹角。

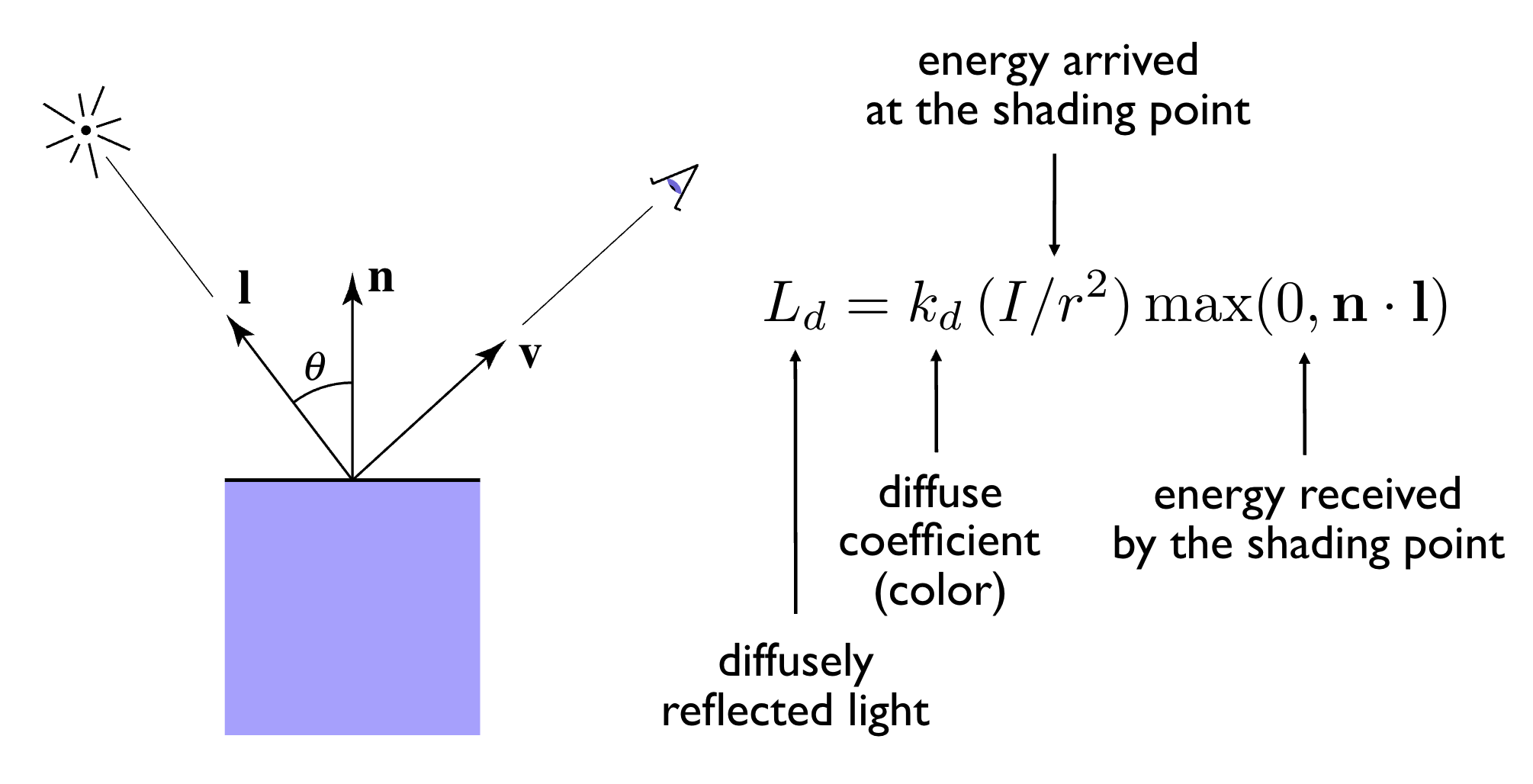
数学公式： L d = k d ⋅ ( I / r 2 ) ⋅ max ⁡ ( 0 , n ⋅ l ) L_d = k_d \cdot (I/r^2) \cdot \max(0, n \cdot l) Ld=kd⋅(I/r2)⋅max(0,n⋅l)

各参数含义：

k d k_d kd：漫反射系数（取值 0-1），决定表面漫反射能力，通常与表面颜色相关；

I / r 2 I/r^2 I/r2：着色点接收的光能量，遵循平方衰减定律（光线强度随距离平方递减）；

n ⋅ l n \cdot l n⋅l：法向量 n 与入射光线方向 l 的点积，反映光线照射角度（垂直照射时效果最强）；

max ⁡ ( 0 , ⋅ ) \max(0, \cdot) max(0,⋅)：避免光线从背面照射时产生负亮度。

示例：光线强度随距离平方递减。

2.1.2 高光项（Specular Term）

高光项用于模拟光滑表面的镜面反射效果，亮度集中在反射方向附近，且强烈依赖观察方向。Blinn-Phong 模型通过 "半向量" 简化了传统 Phong 模型的计算，效率更高。

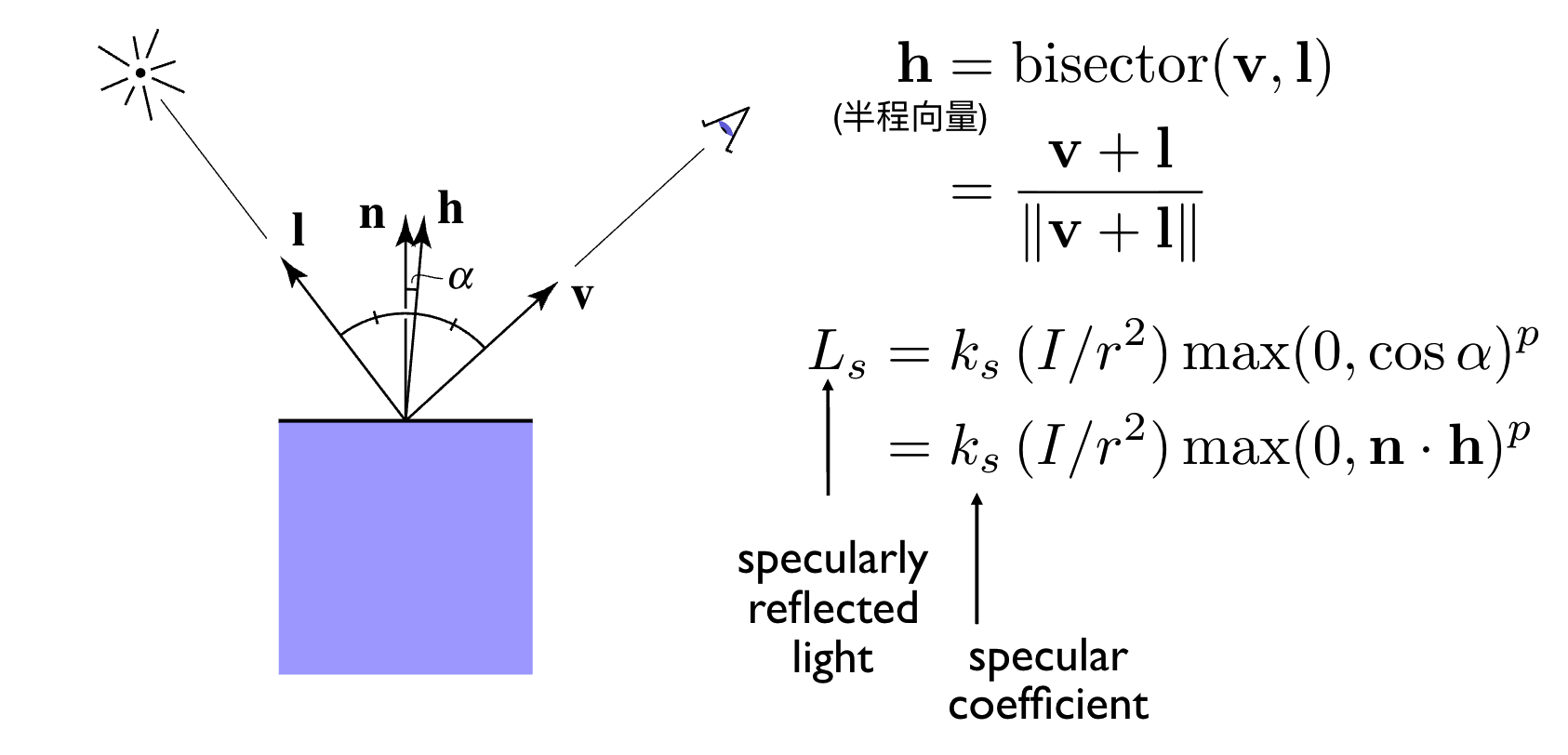
核心思想：引入半向量 h（入射光线方向 l 与观察方向 v 的角平分线），当 h 与法向量 n 接近时，高光最强；

数学公式： L s = k s ⋅ ( I / r 2 ) ⋅ max ⁡ ( 0 , n ⋅ h ) p L_s = k_s \cdot (I/r^2) \cdot \max(0, n \cdot h)^p Ls=ks⋅(I/r2)⋅max(0,n⋅h)p

各参数含义：

k s k_s ks：高光系数（取值 0-1），决定表面镜面反射能力；

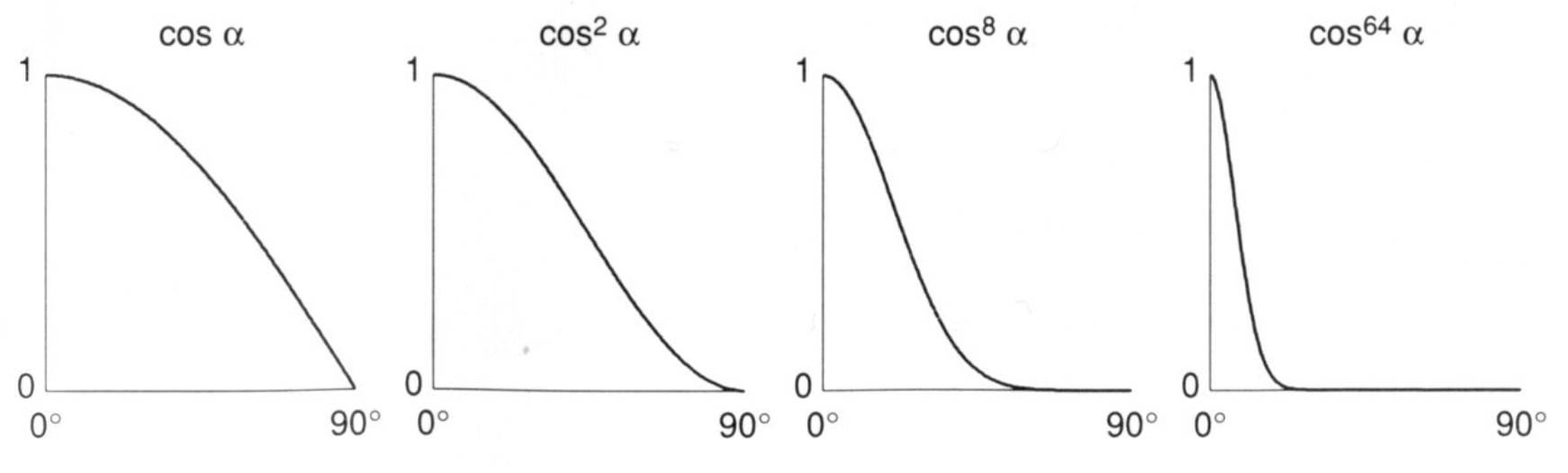
p p p：高光指数，控制高光区域的大小（p 越大，高光越集中，表面越显光滑）；

n ⋅ h n \cdot h n⋅h：法向量与半向量的点积，反映高光强度。

max ⁡ ( 0 , ⋅ ) \max(0, \cdot) max(0,⋅)：避免光线从背面照射时产生负亮度。

示例：p 越大，高光越集中，表面越显光滑

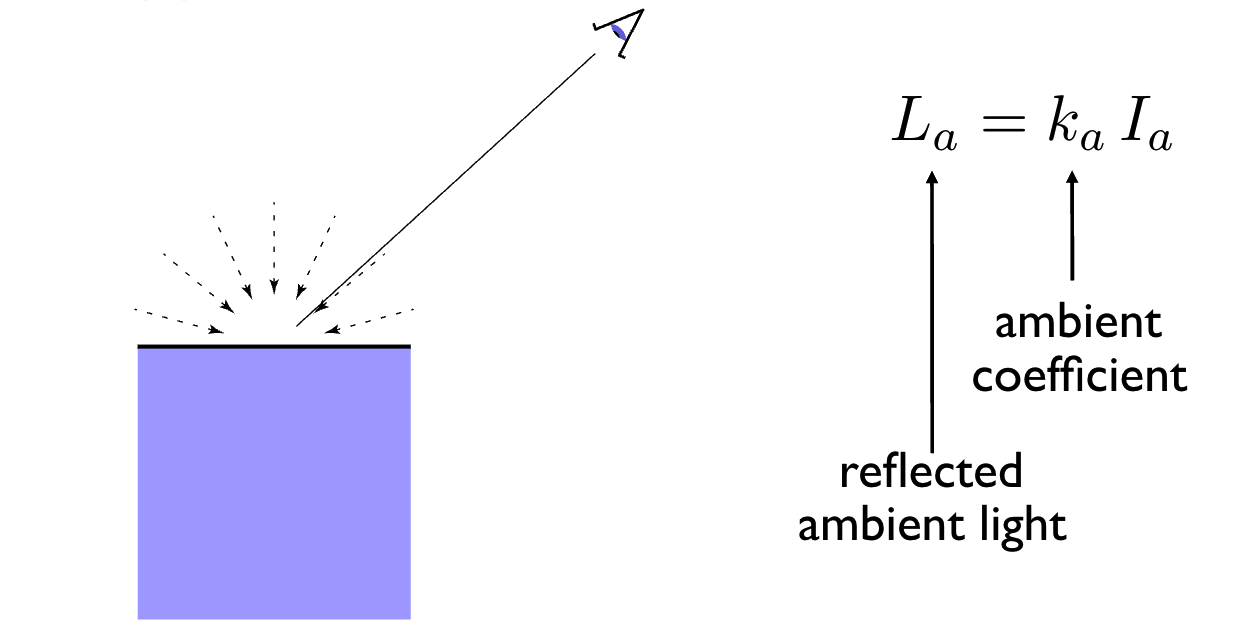
2.1.3 环境光项（Ambient Term）

现实场景中，物体除了直接接收光源照射，还会受到环境中多次反射的间接光照。环境光项是一种简化模拟，用于填补直接光照产生的阴影，避免画面出现纯黑区域。

数学公式： L a = k a ⋅ I a L_a = k_a \cdot I_a La=ka⋅Ia

各参数含义：

k a k_a ka：环境光系数（取值 0-1），决定表面接收环境光的能力；

I a I_a Ia：环境光强度，为全局常量。

注意：环境光项是近似模拟（并非物理真实），仅用于提升画面合理性。

2.1.4 完整Blinn-Phong 反射模型（Blinn-Phong Reflection Model）

Blinn-Phong 模型的最终亮度为三个分量之和：

L = L a + L d + L s = k a I a + k d ( I / r 2 ) max ⁡ ( 0 , n ⋅ l ) + k s ( I / r 2 ) max ⁡ ( 0 , n ⋅ h ) p L = L_a + L_d + L_s = k_a I_a + k_d (I/r^2) \max(0, n \cdot l) + k_s (I/r^2) \max(0, n \cdot h)^p L=La+Ld+Ls=kaIa+kd(I/r2)max(0,n⋅l)+ks(I/r2)max(0,n⋅h)p

2.2 着色频率（Shading Frequencies）

着色频率指 "在哪个层级计算光照"，不同频率直接影响画面光滑度与计算效率，常见的有三种方式。

2.2.1 平面着色（Shade each triangle (flat shading)）

着色层级：每个三角形面（Face）

核心逻辑：为每个三角形分配一个法向量（面法向量），整个三角形使用同一光照计算结果；

优点：计算效率极高（每个三角形仅需一次光照计算）；

缺点：画面呈现明显的 "三角形分割感"，无法表现光滑表面（如球体、圆柱体）。

示例：

2.2.2 Gouraud着色（Shade each vertex (Gouraud shading)）

着色层级：每个顶点（Vertex）

核心逻辑：

为每个顶点计算法向量（可通过周围面法向量平均得到）；

在顶点处执行光照计算，得到顶点颜色；

三角形内部的像素颜色通过顶点颜色插值得到；

优点：效率中等，画面比平面着色光滑；

缺点：高光效果可能失真（插值过程会模糊高光细节）。

示例：

2.2.3 Phong 着色（Shade each pixel (Phong shading)）

着色层级：每个像素（Pixel）

核心逻辑：

顶点法向量通过 barycentric 插值得到三角形内部每个像素的法向量（需归一化）；

对每个像素执行完整的 Blinn-Phong 模型计算；

注意：此处的 "Phong 着色" 是着色频率，并非上一讲的 "Phong 反射模型"；

优点：画面最光滑，高光效果精准，是实时渲染的主流选择；

缺点：计算量最大（每个像素都需执行光照计算）。

示例：

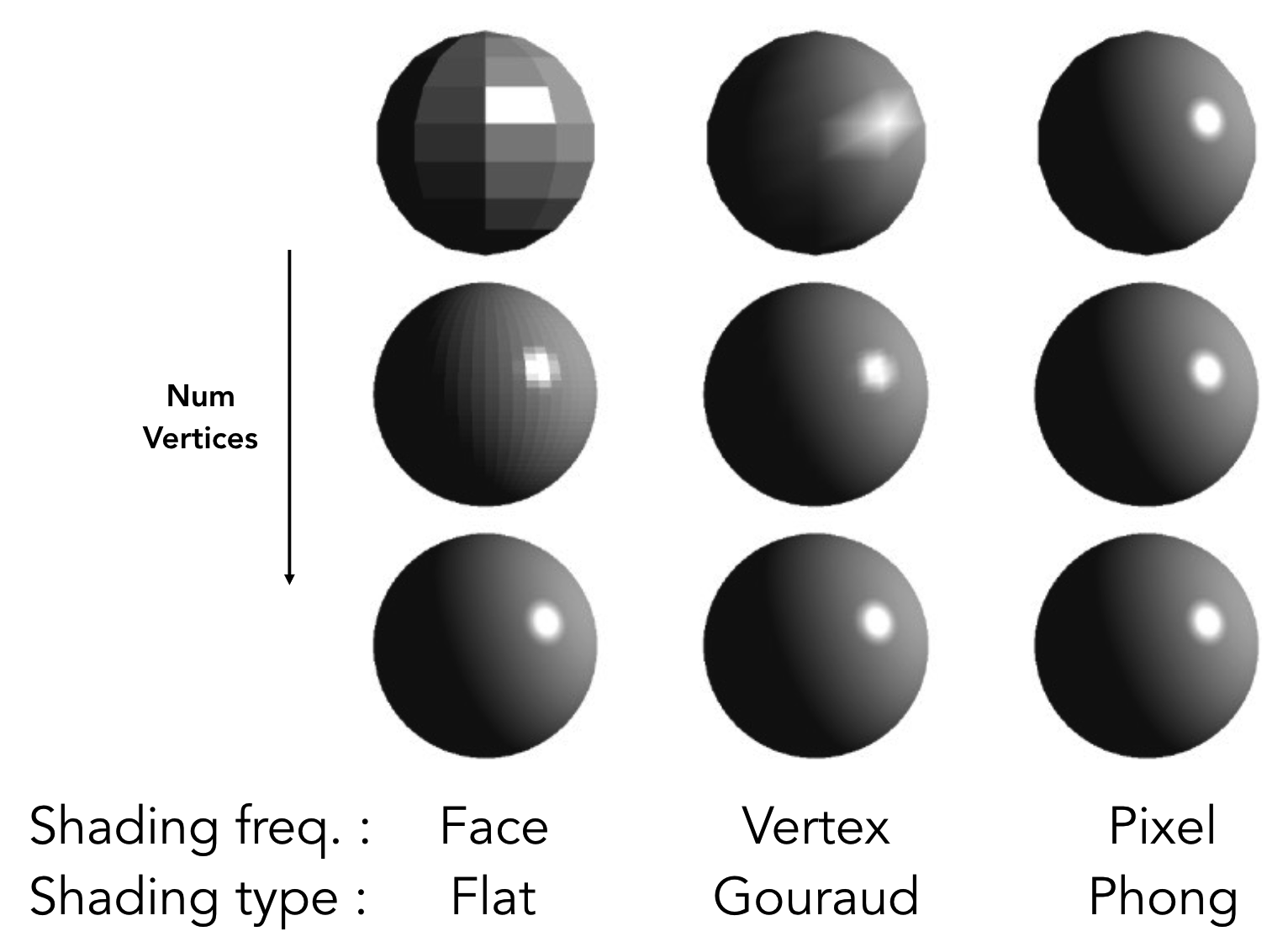
2.2.4 三种着色方法的对比

着色方式	着色层级	画面效果	计算效率
平面着色	三角形面	粗糙，有分割感	最高
Gouraud 着色	顶点	较光滑，高光可能失真	中等
Phong 着色	像素	最光滑，高光精准	最低

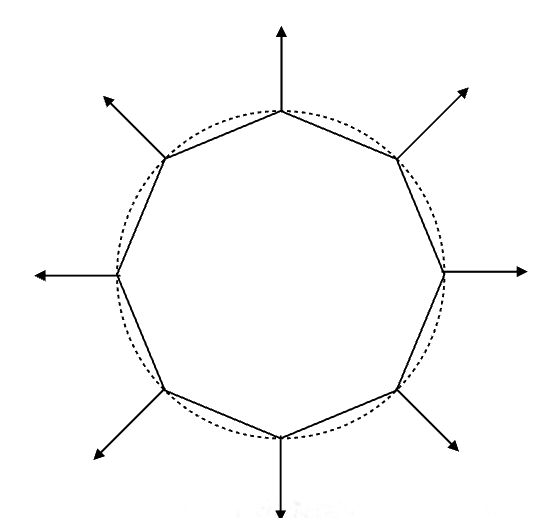
2.2.5 补充：定义每个顶点的法向量（Defining Per-Vertex Normal Vectors）

顶点法向量（Per-Vertex Normal Vectors）是 3D 模型每个顶点对应的单位向量，用于表征顶点所在光滑表面的真实朝向，是 Gouraud 着色（顶点着色）和 Phong 着色（像素着色）的关键基础 ------ 直接影响光照计算的准确性和表面着色的光滑度，区别于平面着色中单一的 "面法向量"。

优先方案：从底层几何直接获取

适用场景：模型有明确的原始几何定义（如数学公式描述的球体、参数曲面）；

核心逻辑：通过几何公式计算顶点的真实法向量，无需近似；

示例：球体的顶点法向量方向为 "从球心指向顶点"，天然垂直于球体表面。

近似方案：通过周围面法向量平均计算

当模型为离散三角形拼接而成（无原始光滑几何信息，如 3D 扫描模型、手工多边形模型）时，采用此主流方案，步骤如下：确定相邻三角形：找到所有包含目标顶点的三角形（即顶点所属的全部三角形）；计算面法向量：对每个相邻三角形，通过其三个顶点的位置向量叉乘，得到该三角形的面法向量(N_i)，并归一化（确保为单位向量）；向量求和与归一化：将所有相邻三角形的面法向量求和，再对求和结果做归一化处理，最终得到顶点法向量。

2.3 实时渲染管线（Graphics Pipeline）

渲染管线是将 3D 场景转换为 2D 图像的流程，现代 GPU 会并行执行该流程的各个阶段，确保实时性（30-60 FPS，VR 场景要求更高）。

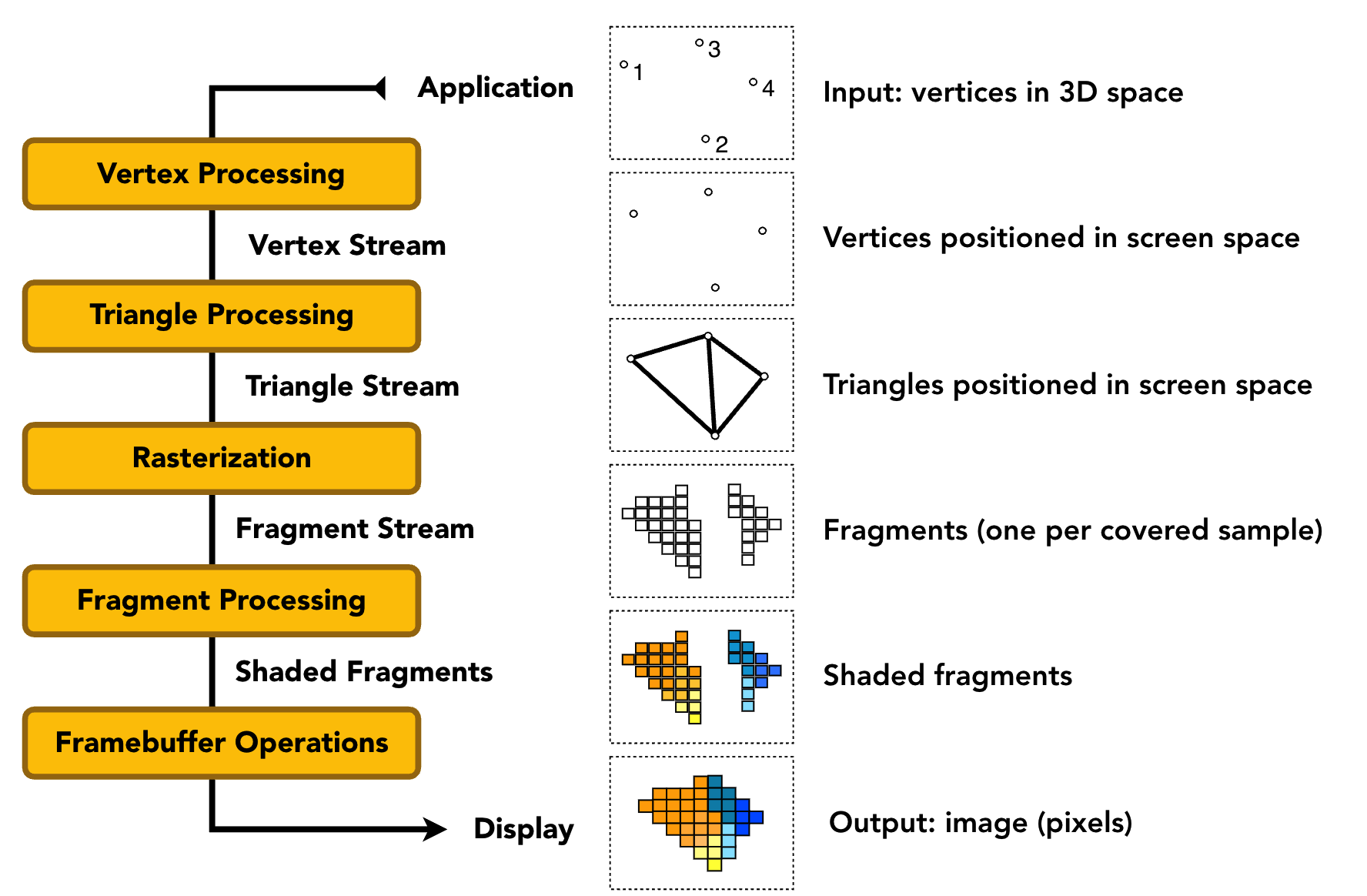
2.3.1 管线各核心阶段

1️⃣ 应用阶段（Application）

运行在 CPU 上，负责场景准备工作：

定义 3D 模型的顶点数据（位置、法向量、纹理坐标等）；

设置光源参数、相机位置；

输出顶点流（Vertex Stream）到下一阶段。

2️⃣ 顶点处理（Vertex Processing）

对每个顶点执行变换操作：

模型变换（Model）：将顶点从模型空间转换到世界空间；

视图变换（View）：将世界空间顶点转换到相机空间；

投影变换（Projection）：将相机空间顶点转换到裁剪空间；

最终输出屏幕空间的顶点位置。

3️⃣ 三角形处理（Triangle Processing）

将顶点流组装为三角形（每个三角形由 3 个顶点组成）；

执行裁剪操作（剔除屏幕外的三角形）；

输出三角形流（Triangle Stream）。

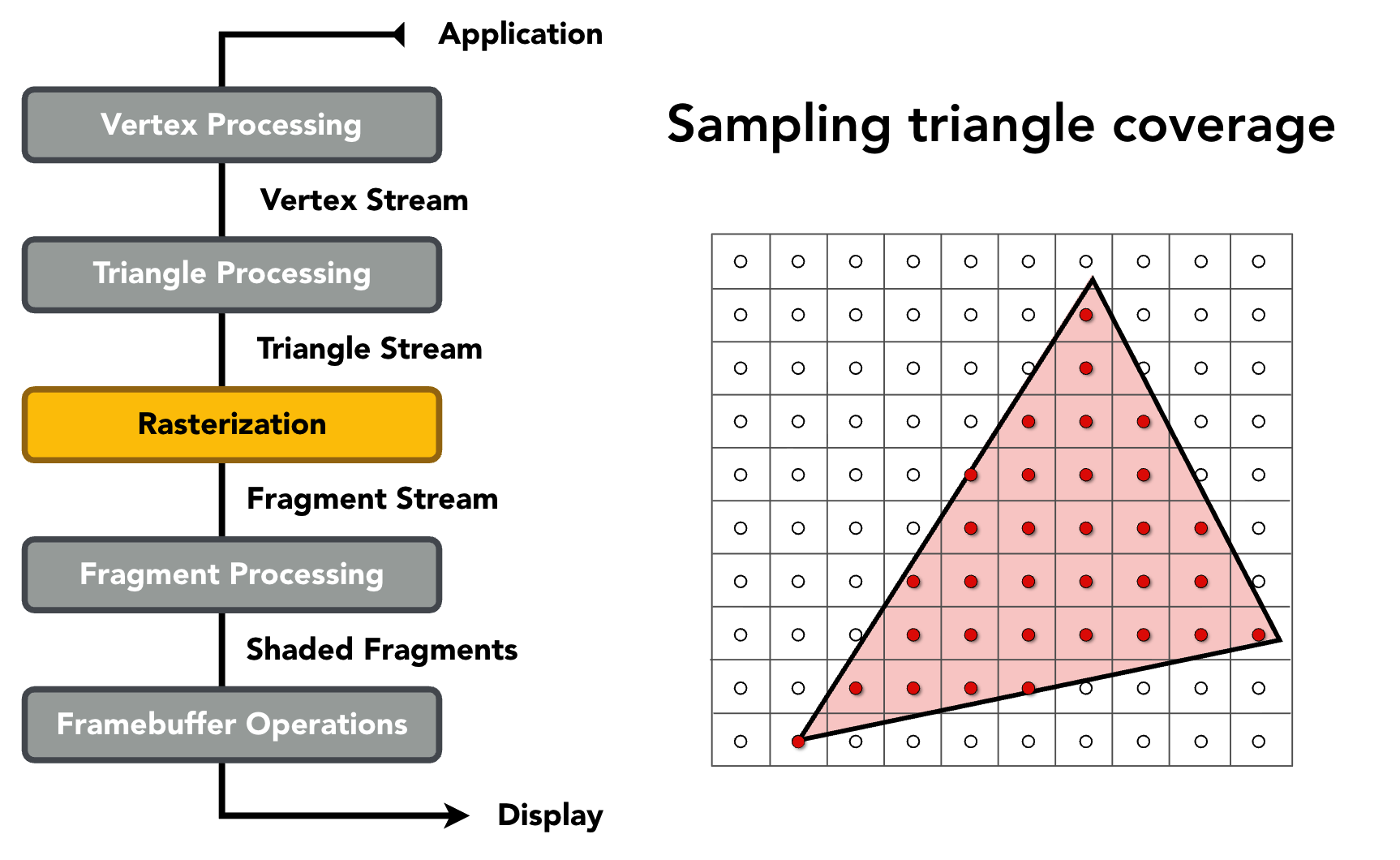
4️⃣ 光栅化（Rasterization）

核心任务：将三角形转换为像素（片段 Fragment）；

采样三角形覆盖的像素位置，生成片段流（Fragment Stream）；

每个片段包含像素位置、插值后的法向量、纹理坐标等信息。

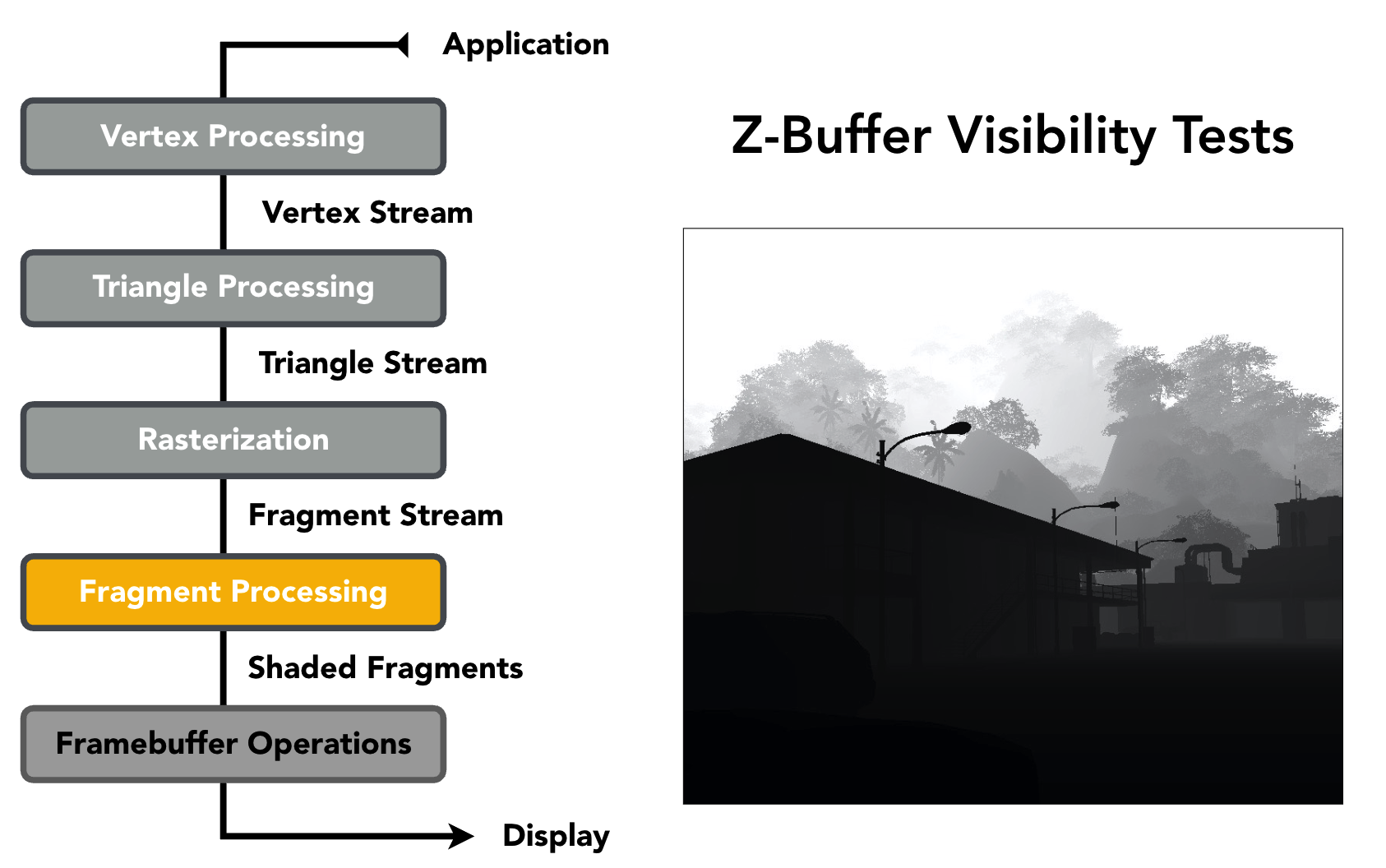
5️⃣ 片段处理（Fragment Processing）

对每个片段执行着色计算：

执行片段着色器（Shader）：结合 Blinn-Phong 模型、纹理映射计算片段颜色；

执行深度测试（Z-Buffer）：剔除被遮挡的片段；

输出着色后的片段（Shaded Fragments）。

6️⃣ 帧缓冲操作（Framebuffer Operations）

合并片段颜色（如透明度混合）；

将最终颜色写入帧缓冲（Framebuffer）；

输出图像到显示器。

2.3.2 着色器（Shader Programs）

着色器是运行在 GPU 上的程序，用于自定义管线中的顶点处理和片段处理阶段，常见的有：

顶点着色器（Vertex Shader）：处理顶点变换、传递插值数据（如纹理坐标、法向量）；
片段着色器（Fragment Shader）：计算片段颜色，是实现光照、纹理的核心。

示例：GLSL 漫反射片段着色器

cpp 复制代码

uniform sampler2D myTexture; // 纹理采样器
uniform vec3 lightDir;       // 光源方向（全局参数）
varying vec2 uv;             // 插值后的纹理坐标
varying vec3 norm;           // 插值后的法向量

void main() {
    vec3 kd = texture2D(myTexture, uv).rgb; // 从纹理获取材料颜色
    float diffuse = clamp(dot(-lightDir, norm), 0.0, 1.0); // Lambert漫反射模型计算
    gl_FragColor = vec4(kd * diffuse, 1.0); // 输出片段颜色
}

着色器函数每个片段执行一次。

输出当前片段对应屏幕采样位置处的表面颜色。

该着色器执行纹理采样，获取该位置处表面的材质颜色，随后执行漫反射光照计算。

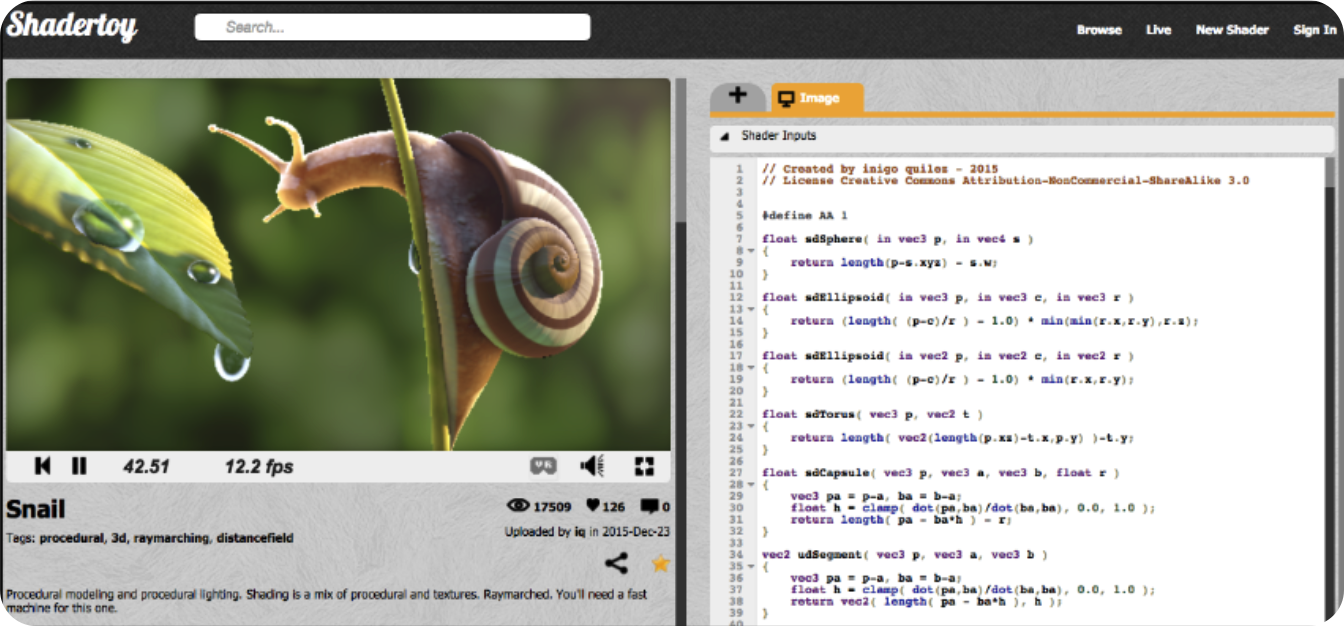
示例：蜗牛着色器程序（Snail Shader Program）。

Procedurally modeled, 800 line shader. http://shadertoy.com/view/ld3Gz2

目标是实时呈现高度复杂的3D场景。但存在以下挑战：

一个场景中包含数十万个到数百万个三角形；

复杂的顶点和片段着色器计算；

高分辨率（200-400万像素 + 超采样）；

每秒30-60帧（虚拟现实场景下甚至更高）；

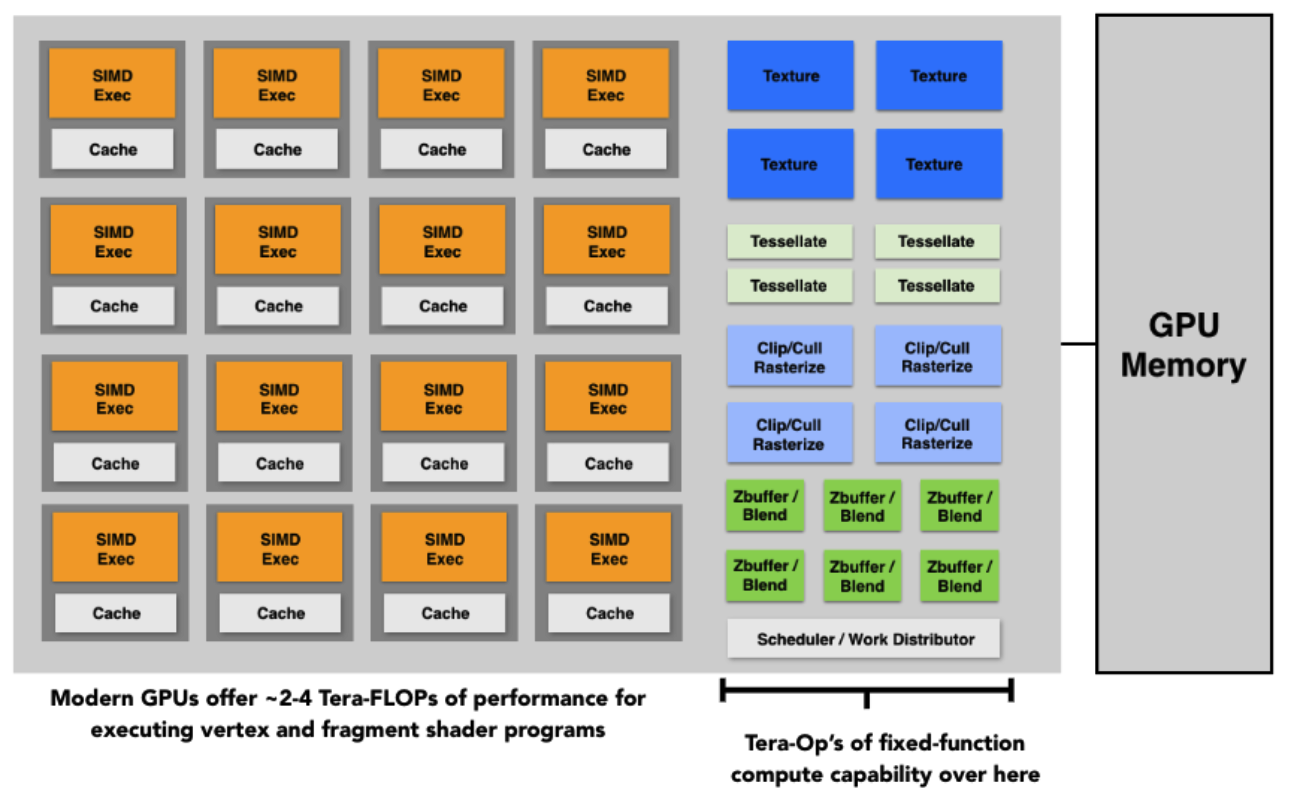
2.3.3 GPU 架构与并行计算（Graphics Pipeline Implementation: GPUs）

GPU 是异构多核处理器，专为并行执行管线阶段设计：

包含大量 SIMD（单指令多数据）核心，可同时处理多个顶点 / 片段；

支持纹理缓存、Z-Buffer 等硬件加速单元；

现代 GPU 性能可达 2-4 TFLOPs，能高效处理百万级三角形场景。

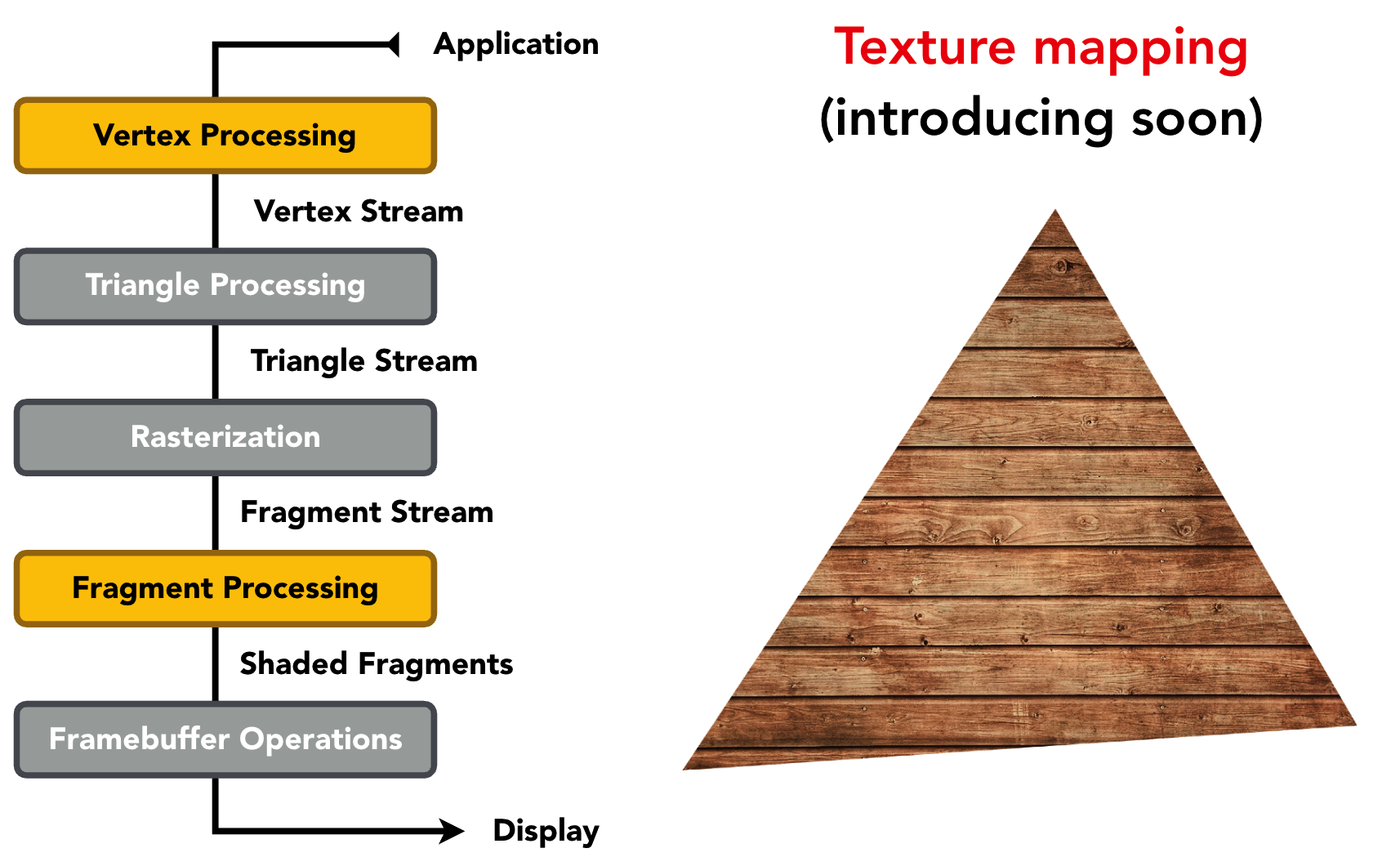
2.4 纹理映射（Texture Mapping）

纹理映射是给 3D 模型表面添加细节的核心技术，通过将 2D 纹理图像 "贴" 到 3D 表面，实现木纹、布料、图案等复杂外观，而无需增加模型顶点数量。

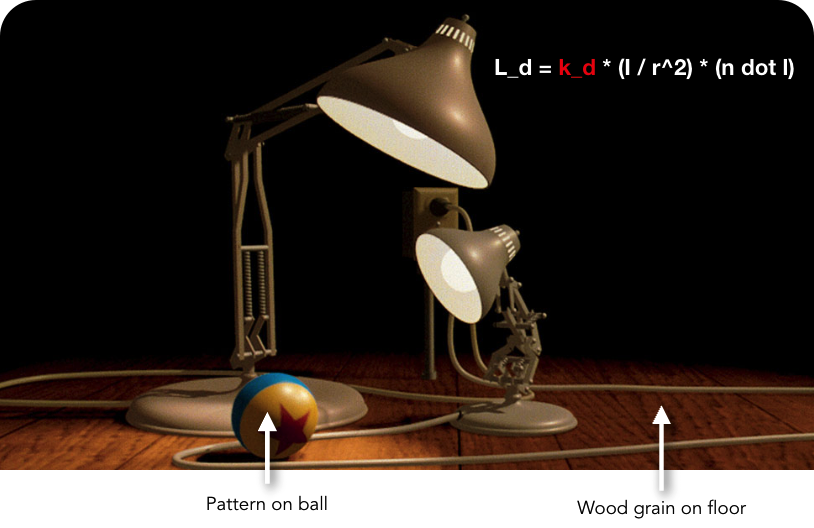
核心原理：

3D 表面的每个顶点都分配一个 2D 纹理坐标（u, v），取值范围通常为 [0, 1]；

纹理坐标定义了顶点在 2D 纹理图像中的位置；

三角形内部像素的纹理坐标通过 barycentric 插值得到；

渲染时，根据像素的纹理坐标从纹理图像中采样颜色，代入 Blinn-Phong 模型计算最终亮度；

纹理空间与映射关系（Surfaces are 2D）

曲面存在于三维世界空间中，每个3D表面点在2D图像（纹理）中也有对应的位置。

纹理空间：2D 纹理图像的坐标系统（u 轴水平，v 轴垂直）；

映射流程：3D 世界空间顶点 → 纹理坐标（u, v）→ 纹理图像采样 → 表面颜色。

纹理复用（Tiling，Textures can be used multiple times!）

纹理坐标可超出 [0, 1] 范围，实现纹理重复排列（如地板木纹的连续铺设）；

需在着色器中设置纹理采样模式（重复、镜像、 clamp 等）。

应用效果（Texture Applied to Surface）

无纹理：表面为单一颜色，缺乏细节；

有纹理：表面呈现复杂图案，真实感大幅提升。

三、疑难点整理总结

待补充。

写在最后

💗 感谢各位 📖 读者的支持，如果觉得文章对你有用，请 ♥️ 点赞 🌟 收藏，笔者将不胜感激 🌹～