文章目录
-
- 【`获取资源`请见文章第5节:资源获取】
- [1. 原始金豺优化算法](#1. 原始金豺优化算法)
-
- [1.1 种群初始化](#1.1 种群初始化)
- [1.2 搜寻接近猎物](#1.2 搜寻接近猎物)
- [1.3 包围驱赶猎物](#1.3 包围驱赶猎物)
- [1.4 猛扑并擒获猎物](#1.4 猛扑并擒获猎物)
- [2. 改进金豺优化算法](#2. 改进金豺优化算法)
-
- [2.1 动态折射反向学习](#2.1 动态折射反向学习)
- [2.2 黄金正弦策略](#2.2 黄金正弦策略)
- [2.3 自适应能量因子](#2.3 自适应能量因子)
- [3. 部分代码展示](#3. 部分代码展示)
- [4. 仿真结果展示](#4. 仿真结果展示)
- [5. 资源获取](#5. 资源获取)
【获取资源请见文章第5节:资源获取】
1. 原始金豺优化算法
金豺优化算法GJO(Golden Jackal Optimization)是 Chopra 等于 2022 年提出的一种元启发式算法,其通过模拟金豺群体协同捕食行为(搜索、包围、攻击)实现优化。 相较传统算法,GJO 具有控制参数少、实现简单等优势,已成功应用于高维特征选择、机器人路径规划、人流量预测及软件定义网络等领域。
1.1 种群初始化
GJO算法中定义了 n 个猎物,每个猎物的位置信息代表一个潜在解。 假设初始时刻猎物在搜索空间上随机均匀分布,可表示为:
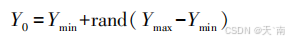
Y0为猎物初始种群的位置;rand 是[0,1]范围内的随机数;Ymax 和 Ymin 分别是求解问题的上下边界。
金豺狩猎行为由雄豺领导,雌豺跟随其狩猎,其中最佳位置代表雄豺位置 YM( t),次佳位置的代表雌豺位置 YFM(t)。算法中,选择每次迭代排名前2位结果生成雄、雌金豺更新前的位置,利用猎物的逃脱能量E来更新猎物位置。猎物逃脱能量E的表达式为:
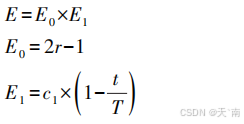
式中:E1表示猎物能量的下降过程;E0表示猎物能量的初始状态;r表示(0,1)间随机数;t表示当前迭代次数;T表示最大迭代次数;c1是等于1. 5的常值。
1.2 搜寻接近猎物
当金豺与食物的距离过大且周围没有食物时,金豺将采用随机游走策略进行位置更新位置,数学模型如下:
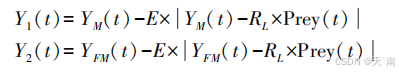
1.3 包围驱赶猎物
当猎物遭受攻击时,猎物逃逸能量E持续衰减,触发金豺群体执行协同围捕行为。雄性和雌性金豺一起捕猎的行为的数学模型如下:
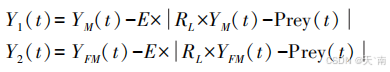
1.4 猛扑并擒获猎物
最终迭代完成时,雄豺的位置即为全局最优解。
2. 改进金豺优化算法
2.1 动态折射反向学习
动态折射反向学习策略的思想来自于凸透镜成像的原理。通过基于当前坐标生成一个反向位置来扩展搜索范围,如图1所示。

图1 透镜成像折射反向学习原理图
在二维坐标中,x轴的搜索范围为(a, b), y轴表示一个凸透镜。假设物体A在x轴上的投影为x,高度为h,通过透镜成像,另一侧的图像为A*, A在x轴上的投影为x ,高度为h*。通过以上分析,我们可以得到如下公式:
( a + b ) / 2 − x x ∗ − ( a + b ) / 2 = h h ∗ \frac{(a+b)/2-x}{x^{*}-(a+b)/2 }=\frac{h}{h^{*}} x∗−(a+b)/2(a+b)/2−x=h∗h
对公式(2)进行转换,即可得到反向解x*的表达式为:
x ∗ = a + b 2 + a + b 2 k − x k x^{*} =\frac{a+b}{2}+\frac{a+b}{2k}-\frac{x}{k} x∗=2a+b+2ka+b−kx
其中, k = h / h ∗ k=h/h^{*} k=h/h∗, a a a和 b b b可以视为某维度的上下限。本文中的 k k k是一个与迭代次数相关的动态自适应值。
2.2 黄金正弦策略
受到正弦函数的启发,利用数学中的正弦函数进行迭代寻优,具有较强的全局搜索能力,同时在位置更新过程中引入黄金分割系数来使算法能够对局部区域进行充分搜索,使全局搜索和局部开发能力达到良好的平衡。下面是金豺个体利用黄金正弦策略进行位置更新的公式:
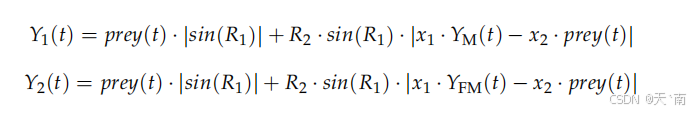
2.3 自适应能量因子
标准 GJO 算法采用线性衰减模式调控能量参数 E1,其固定衰减特性难以有效协调全局勘探与局部开发间的动态平衡。具体表现为:过早进入包围猎物阶段,迫使算法提前锁定局部区域,陷入局部寻优。 因此,本文提出一种自适应变化的 E1 表达式来进行逃逸能量调控:
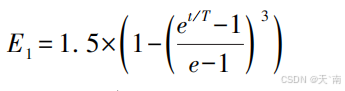
3. 部分代码展示
matlab
%% 清除环境变量
clear;
close all;
clc;
%% 参数设置
N = 30; % 种群规模
Function_name = 'F4'; % 从F1到F23的测试函数的名称
Max_iteration = 500; % 最大迭代次数
cnt_max = 2;
% 加载所选基准函数的详细信息
[lb, ub, dim, fobj] = Get_Functions_details(Function_name);
Curve_GJO = zeros(1,Max_iteration);
Curve_IGJO = zeros(1,Max_iteration);
for cnt = 1:cnt_max
% 初始化种群位置
X = initialization(N, dim, ub, lb);
[GJO_Best_score(cnt), GJO_Best_pos(cnt, :), GJO_Curve]= GJO(X,N,Max_iteration,lb,ub,dim,fobj);
[IGJO_Best_score(cnt), IGJO_Best_pos(cnt, :),IGJO_Curve]=IGJO(X,N,Max_iteration,lb,ub,dim,fobj);
Curve_GJO = Curve_GJO+GJO_Curve;
Curve_IGJO = Curve_IGJO+IGJO_Curve;
end
Curve_GJO = Curve_GJO/cnt_max;
Curve_IGJO = Curve_IGJO/cnt_max;
std_GJO = std(GJO_Best_score);
std_IGJO = std(IGJO_Best_score);
worst_GJO = max(GJO_Best_score);
worst_IGJO = max(IGJO_Best_score);
best_GJO = min(GJO_Best_score);
best_IGJO = min(IGJO_Best_score);
mean_GJO = mean(GJO_Best_score);
mean_IGJO = mean(IGJO_Best_score);
%% 画图
% 1、画出所选基准函数的三维立体图形
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(Function_name);
title(Function_name)
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
% 2、画出目标函数值变化曲线图
subplot(1,2,2);
t = 1:Max_iteration;
semilogy(t, Curve_GJO, 'g-',t, Curve_IGJO, 'r-','linewidth', 1.5);
title(Function_name);
xlabel('Iteration');
ylabel('Mean of objective function values');
axis fill
grid on
box on
legend( 'GJO', 'IGJO');
%% 显示结果
disp(['函数:', num2str(Function_name)]);
disp(['GJO:最差值: ', num2str(worst_GJO), ', 最优值: ', num2str(best_GJO), ', 平均值: ', num2str(mean_GJO), ', 标准差: ', num2str(std_GJO)]);
disp(['IGJO:最差值: ', num2str(worst_IGJO), ', 最优值: ', num2str(best_IGJO), ', 平均值: ', num2str(mean_IGJO), ', 标准差: ', num2str(std_IGJO)]);4. 仿真结果展示
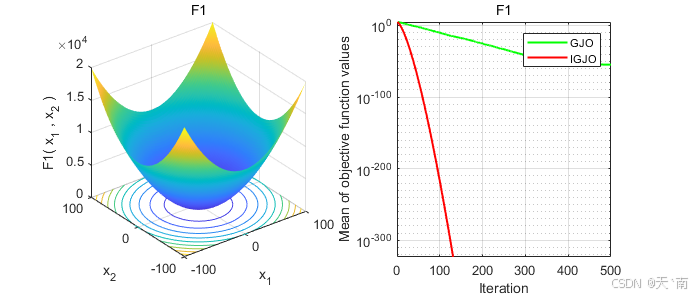
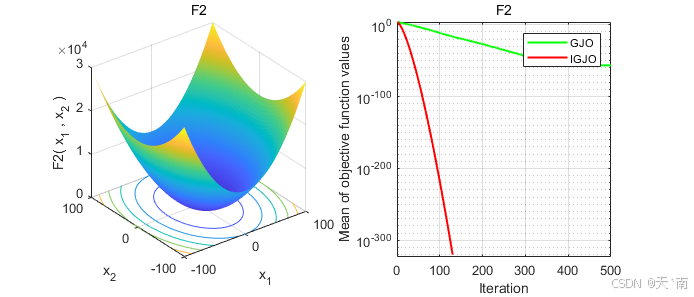
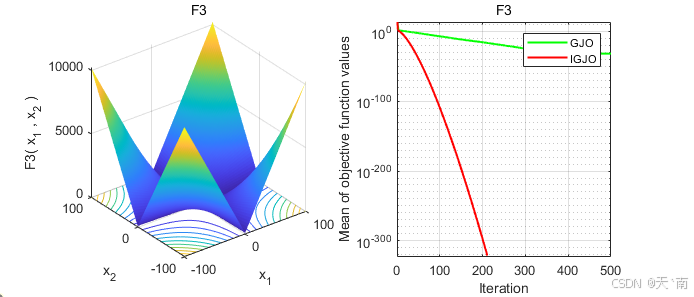
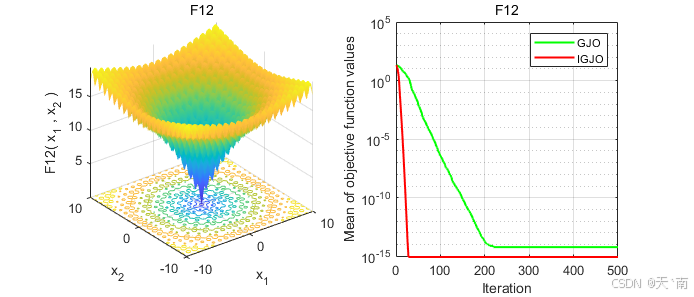
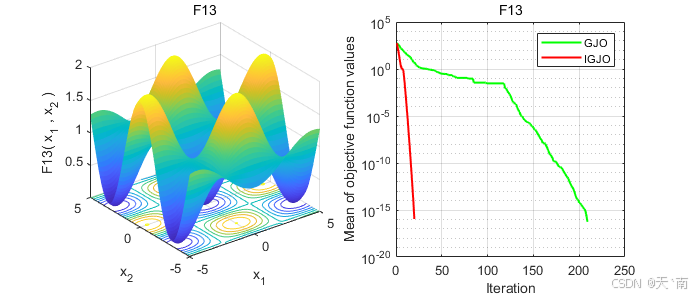
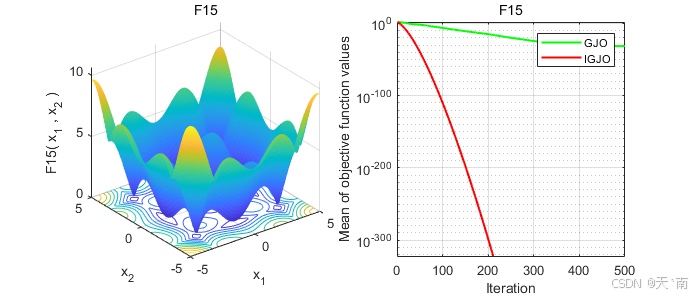
5. 资源获取
可更换其他群智能优化算法,获取完整代码资源。👇👇👇👀名片