车对车对向交汇场景的毫米波路径损耗建模论文精读
A. Ghosh et al., "Vehicle-to-Vehicle Path Loss Modeling at Millimeter-Wave Band for Crossing Cars," in IEEE Antennas and Wireless Propagation Letters, vol. 22, no. 9, pp. 2125-2129, Sept. 2023, doi: 10.1109/LAWP.2023.3277961.
场景与动机:为什么对向交汇的 V2V 在毫米波下值得单独建模
对向交汇属于"通信时间窗极短"的典型 V2V 场景:两车相向而行,相对速度相加 ,能进入有效通信范围的时间很短。如果要在这段短窗口里完成更大体量的数据交换(例如前向碰撞预警、意图共享、传感器信息交换),链路往往需要更大的带宽,毫米波因其宽带潜力而成为候选。问题在于:毫米波传播对遮挡、几何关系、天线位置更敏感,车辆在接近与远离阶段的几何/散射格局并不完全"时间反演对称",因此路径损耗曲线可能出现系统性差异。论文的目标不是构建复杂的几何射线模型,而是以测量驱动的方式给出一个可用于工程建模的 PL 表达式,并验证其在 approaching / departing 两阶段的有效性。
外场测量与数据来源:从声探到"可用于拟合的 PL 序列"
论文使用的是时域宽带信道声探方案(time-domain channel sounder),核心思想是发射一段具有良好自相关/互补特性的已知序列(这里是 Golay 互补序列),在接收端做相关处理以获得信道冲激响应(CIR),再由 CIR 估计接收功率并换算成路径损耗。
测试地点与车辆配置
测量在捷克 Brno University of Technology 校园道路完成,现场无其他车辆和显著运动物体,可保证环境统计特性相对平稳且全程 LOS(视距)可获得。两辆车分别搭载 Tx 与 Rx 设备,天线通过吸盘固定在车辆驾驶员侧位置。由于示波器耗电较大,Rx 车后方还连接拖车以提供额外电源。
图 1:测试场地、轨迹与车辆/天线实景
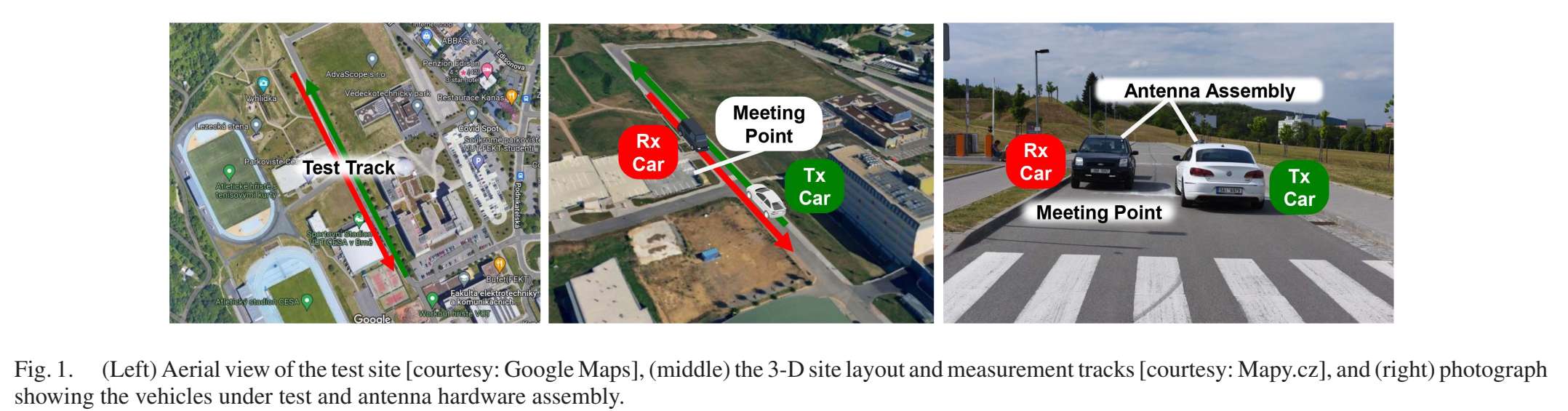
图中左侧给出测试道路的俯视图与行驶轨迹,中间是三维场地与测量轨迹示意,右侧是两车会车点附近的实拍图,标注了 Tx/Rx 车辆位置与天线组件位置。"Meeting Point"对应两车交汇处。
波形与采样参数(论文给出了一组可复算的链路采样量)
Golay 序列数据率为
RDR=12.5 Gbps,N=2048 bits. R_{\mathrm{DR}}=12.5~\text{Gbps}, \qquad N=2048~\text{bits}. RDR=12.5 Gbps,N=2048 bits.
由此最大可观测时延窗口(决定可解析的最大多径时延范围)为
Tmax=NRDR=204812.5×109≈163.8 ns. T_{\max}=\frac{N}{R_{\mathrm{DR}}} =\frac{2048}{12.5\times 10^{9}} \approx 163.8~\text{ns}. Tmax=RDRN=12.5×1092048≈163.8 ns.
示波器采样率为
RS=50 GSample/s. R_{\mathrm{S}}=50~\text{GSample/s}. RS=50 GSample/s.
每条 CIR 的采样点数由"采样率/码率"的过采样比例决定:
Nsam/CIR=N⋅RSRDR=2048×5012.5=2048×4=8192. N_{\mathrm{sam/CIR}} = N\cdot \frac{R_{\mathrm{S}}}{R_{\mathrm{DR}}} = 2048\times \frac{50}{12.5} =2048\times 4 =8192. Nsam/CIR=N⋅RDRRS=2048×12.550=2048×4=8192.
论文进一步给出每次测量可获得的 CIR 数量 NCIR/meas≈468N_{\mathrm{CIR/meas}}\approx 468NCIR/meas≈468,以及总测量时长 Tmeas≈2.34 msT_{\mathrm{meas}}\approx 2.34~\text{ms}Tmeas≈2.34 ms。将这两个量结合可反推相邻 CIR 的时间间隔约为 2.34 ms/468≈5 μs2.34\text{ ms}/468\approx 5~\mu\text{s}2.34 ms/468≈5 μs,这一量级与时域声探对快时变信道的采样逻辑相一致:相邻 CIR 之间间隔足够短,使得车辆运动引起的几何变化在单次测量窗口内可被细致采样。
速度与试验次数
共 6 次对向交汇:其中 4 次相对速度 50 km/h(13.89 m/s),2 次相对速度 70 km/h(19.44 m/s)。每次开始时 Tx-Rx 初始间距约 35 m。相对速度不同会导致会车点在"起始点坐标系下"的位置不同,这一点在图 3 的横轴跨度差异上可观察到。
从"对向交汇"的几何到 PL 的典型轨迹
论文用"相对距离"刻画对向交汇过程:会车点定义为相对距离 0;相对距离为负表示两车仍在接近(approaching),为正表示已经远离(departing)。
图 2:对向交汇过程的 PL 轨迹示例
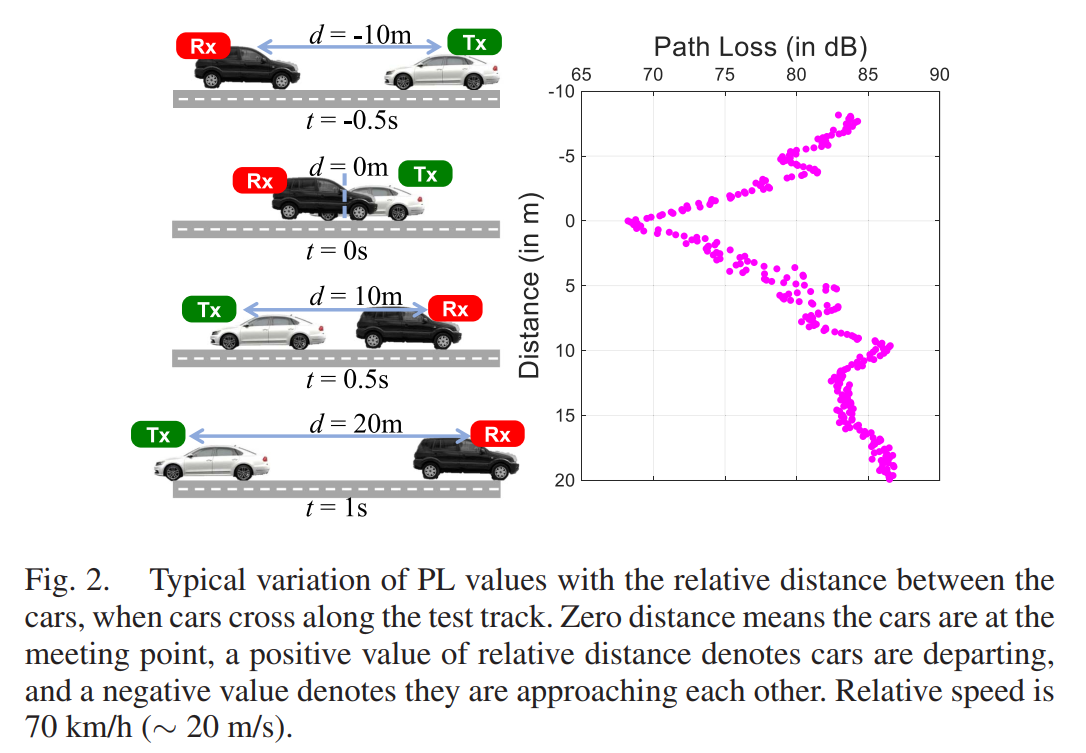
图左用多个时刻示意相对距离从负到正的变化;图右给出 PL(横轴,dB)随相对距离(纵轴,m)的变化点云。点云并非单调光滑曲线,反映了近距离区域多径干涉、车体散射与测量噪声共同作用下的起伏,但总体趋势仍随距离增大而损耗增大。
四类标准路径损耗模型:形式、含义与"会车场景"里的局限
论文将自身模型与四类常见 PL 模型对照。统一采用 dB 域表达,并用一个高斯项描述大尺度阴影衰落(shadow fading):
Xσ∼N(0,σ2). X_{\sigma}\sim\mathcal{N}(0,\sigma^2). Xσ∼N(0,σ2).
1) 浮动截距模型 FI(Floating Intercept)
PL(d)=α+10βlog10(d)+Xσ.(1) PL(d)=\alpha+10\beta\log_{10}(d)+X_{\sigma}. \tag{1} PL(d)=α+10βlog10(d)+Xσ.(1)
FI 的思路是:把 PLPLPL 对 log10(d)\log_{10}(d)log10(d) 视为一条直线,α\alphaα 与 β\betaβ 直接由数据拟合得到。它的优点是灵活、易拟合;但关键缺点是:式中没有显式频率项,当频段变化或需要与其他频段模型比较时,物理解释较弱。在本文固定 59.6 GHz 的单频段实验里,这个缺点并不意味着一定最差,但论文结果表明 FI 的拟合仍明显落后,原因之一正是它无法用物理可解释的"频率相关项 + 距离项"分解数据变化。
2) 近基准模型 CI(Close-in reference distance)
PL(f,d)=FSPL(f,d0)+10βlog10(dd0)+Xσ,d0=1 m.(2) PL(f,d)=FSPL(f,d_0)+10\beta\log_{10}\Big(\frac{d}{d_0}\Big)+X_{\sigma},\quad d_0=1~\text{m}. \tag{2} PL(f,d)=FSPL(f,d0)+10βlog10(d0d)+Xσ,d0=1 m.(2)
其中自由空间损耗(Free-Space Path Loss)
FSPL(f,d0)=20log10(4πfc), FSPL(f,d_0)=20\log_{10}\Big(\frac{4\pi f}{c}\Big), FSPL(f,d0)=20log10(c4πf),
在 f=59.6 GHzf=59.6~\text{GHz}f=59.6 GHz 且 d0=1 md_0=1~\text{m}d0=1 m 时约为 67.95 dB。CI 的核心是把"1 m 自由空间损耗"当作物理锚点,剩余的距离衰减用一个路径损耗指数(PLE)刻画,因此可解释性强,也更易跨场景复用。
3) ABG 模型(α\alphaα-β\betaβ-γ\gammaγ)
PL(d)=α+10βlog10(dd0)+10γlog10(fcf0)+Xσ,f0=1 GHz.(3) PL(d)=\alpha+10\beta\log_{10}\Big(\frac{d}{d_0}\Big)+10\gamma\log_{10}\Big(\frac{f_c}{f_0}\Big)+X_{\sigma},\quad f_0=1~\text{GHz}. \tag{3} PL(d)=α+10βlog10(d0d)+10γlog10(f0fc)+Xσ,f0=1 GHz.(3)
ABG 通过 γ\gammaγ 引入更通用的频率相关度,理论上适用于多频段联合拟合。但在本文单频点 fc=59.6 GHzf_c=59.6\text{ GHz}fc=59.6 GHz 的场景里,频率项是常数,ABG 的优势难以充分发挥。
4) 3GPP Release 15 的 V2V LOS 城市模型(论文用于对照)
PLLOSurban(d)=38.77+16.7log10(d)+18.2log10(fc)+Xa.(4) PL^{\mathrm{urban}}{\mathrm{LOS}}(d) =38.77+16.7\log{10}(d)+18.2\log_{10}(f_c)+X_a. \tag{4} PLLOSurban(d)=38.77+16.7log10(d)+18.2log10(fc)+Xa.(4)
3GPP 的结构体现了"频率项 + 距离项 + 常数项"的分解。本文关心的是:如果照搬这一结构,是否能解释对向交汇时 approaching / departing 的差异?论文给出的答案是:3GPP 的结构方向是对的,但具体常数项与距离系数在该实测场景下并不最优,需要更贴近数据的参数化。
提出的模型:保留 3GPP 的结构,但把关键项交给数据决定
论文提出的模型形式为
PL(d)=η1+18.2log10(fc)+η2log10(d)+Xσ.(5) PL(d)=\eta_1+18.2\log_{10}(f_c)+\eta_2\log_{10}(d)+X_{\sigma}. \tag{5} PL(d)=η1+18.2log10(fc)+η2log10(d)+Xσ.(5)
可以看到它与式 (4) 的最大差异是:把 3GPP 中固定的 "38.77" 与 "16.7" 替换为可拟合的 η1\eta_1η1 与 η2\eta_2η2。从结构上看,这是一个"频率项保持 3GPP 形式 、但距离衰减斜率与截距针对特定 V2V 对向交汇场景重新标定"的模型。
由于本文实验频率固定为 59.6 GHz,频率项
18.2log10(fc) 18.2\log_{10}(f_c) 18.2log10(fc)
在数值上就是一个常数(若 fcf_cfc 以 GHz 计,则该项约为 32.31 dB)。因此在单频实验里,式 (5) 可理解为"对 log10(d)\log_{10}(d)log10(d) 的线性回归",但它仍保留了与 3GPP 兼容的频率结构,使模型更接近工程标准的表达习惯。
阴影衰落标准差 σ\sigmaσ 按样本标准差估计:
σ=∑i=1N(xi−xˉ)2N−1, \sigma=\sqrt{\frac{\sum_{i=1}^N (x_i-\bar{x})^2}{N-1}}, σ=N−1∑i=1N(xi−xˉ)2 ,
这里 xix_ixi 是样本 PL 值,xˉ\bar{x}xˉ 是样本均值。
评价准则:RMSE 之外,引入"形状相似 + 幅度误差"的复合指标
论文除了使用常规 RMSE 外,还采用两类复合指标,用于强调"曲线形状是否相似"与"数值误差是否足够小"这两个维度。
RMSE(常规误差量纲,dB)
对测量序列 x0(k)x_0(k)x0(k) 与模型预测序列 xi(k)x_i(k)xi(k),RMSE 通常写为
RMSE=1n∑k=1n(xi(k)−x0(k))2. RMSE=\sqrt{\frac{1}{n}\sum_{k=1}^{n}\left(x_i(k)-x_0(k)\right)^2}. RMSE=n1k=1∑n(xi(k)−x0(k))2 .
RMSE 直接刻画 dB 误差的均方根,易于工程解读。
GRG-MAPE:灰关联度与平均绝对百分比误差的加权组合
论文把灰关联度的相似度记为 ρgrg∈[0,1]\rho_{\mathrm{grg}}\in[0,1]ρgrg∈[0,1],再引入由 MAPE 构造的 ρmape\rho_{\mathrm{mape}}ρmape(同样被压到"越大越好"的形式),并组合为
ρgrg−mape=∣α ρgrg+β ρmape∣.(6) \rho_{\mathrm{grg-mape}}=\left|\alpha\,\rho_{\mathrm{grg}}+\beta\,\rho_{\mathrm{mape}}\right|. \tag{6} ρgrg−mape=∣αρgrg+βρmape∣.(6)
其中
ρmape=∣1−Pere∣=∣1−1n∑k=1n∣xi(k)−x0(k)∣x0(k)∣.(7) \rho_{\mathrm{mape}} =\left|1-P_{\mathrm{ere}}\right| =\left|1-\frac{1}{n}\sum_{k=1}^{n}\frac{|x_i(k)-x_0(k)|}{x_0(k)}\right|. \tag{7} ρmape=∣1−Pere∣= 1−n1k=1∑nx0(k)∣xi(k)−x0(k)∣ .(7)
权重取 α=0.1,β=0.9\alpha=0.1,\beta=0.9α=0.1,β=0.9,强调幅度误差(MAPE)对最终判断的主导作用,同时保留一定比例的形状相似度贡献。
PCC-MAPE:皮尔逊相关与 MAPE 的加权组合
类似地,皮尔逊相关系数本来在 [−1,1][-1,1][−1,1] 范围,为了与 GRG 做一致比较,可映射到 [0,1][0,1][0,1] 的相似度 ρpcc\rho_{\mathrm{pcc}}ρpcc,并组合为
ρpcc−mape=∣α ρpcc+β ρmape∣.(8) \rho_{\mathrm{pcc-mape}}=\left|\alpha\,\rho_{\mathrm{pcc}}+\beta\,\rho_{\mathrm{mape}}\right|. \tag{8} ρpcc−mape=∣αρpcc+βρmape∣.(8)
这种"相似度 + 误差"的复合框架隐含的工程动机是:仅靠 RMSE 可能会忽略曲线整体趋势是否一致,而仅靠相关性又可能忽略幅度偏差;组合后可在模型筛选时更稳健。
对照结果:图 3 与表 1 给出的结论非常集中
论文把数据分成 moving in(接近)与 moving away(远离)两类,并在两种相对速度下分别比较五种模型。
图 3:两种速度、两种运动方向下的模型曲线对比
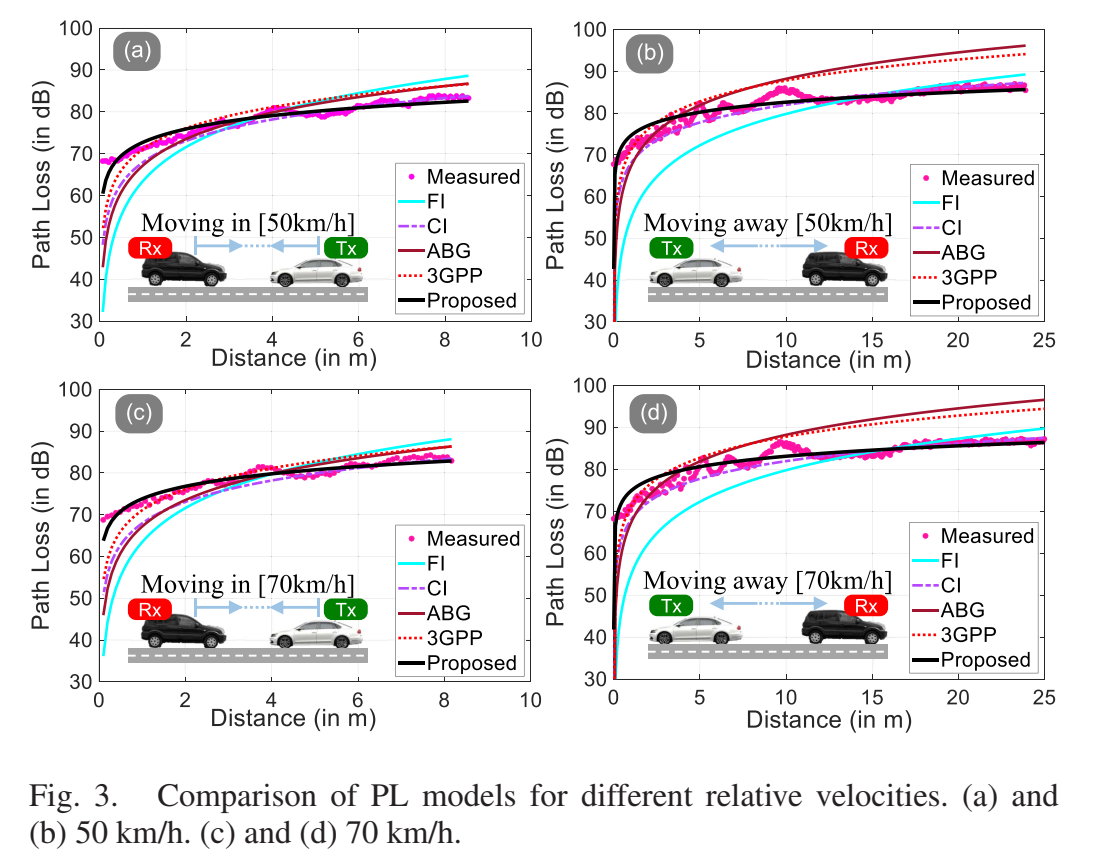
图 3 的四个子图分别对应:
(a) 50 km/h moving in,(b) 50 km/h moving away,© 70 km/h moving in,(d) 70 km/h moving away。图中粉色点为实测,其他曲线为 FI / CI / ABG / 3GPP / Proposed。视觉上 Proposed 曲线在四种情况下都更紧贴点云的总体趋势,尤其在近距离区域对曲线弯曲形态的跟随更好;而 FI 往往偏离较明显。
表 1:拟合优劣的量化指标(RMSE / GRG-MAPE / PCC-MAPE)
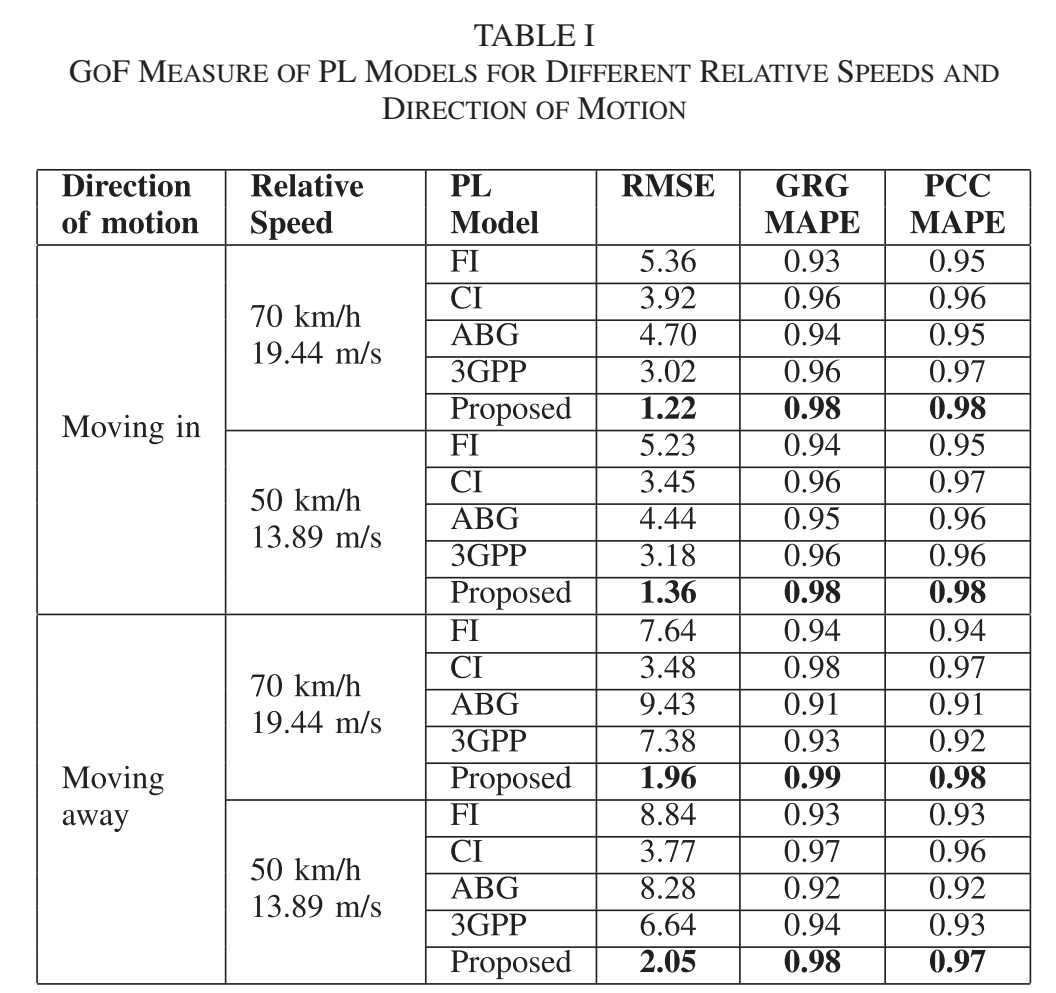
表 1 的信息含量很高:无论是 RMSE 还是两类复合指标,Proposed 在四种场景均给出最优或近最优 ,并且优势在 RMSE 上尤其突出。以表中数值为例:
在 moving in、70 km/h 下,Proposed 的 RMSE 为 1.22 dB ,显著优于 3GPP 的 3.02 dB 、CI 的 3.92 dB 、ABG 的 4.70 dB 、FI 的 5.36 dB ;对应的 GRG-MAPE 与 PCC-MAPE 也达到 0.98 量级。
在 moving away、50 km/h 下,Proposed RMSE 为 2.05 dB ,相比 3GPP 6.64 dB 、CI 3.77 dB 仍有优势,同时复合指标保持在 0.97--0.98 附近。
论文还给出一个解释性判断:FI 在该数据集上表现最差,与其缺少显式频率项有关;在毫米波频段,频率相关项对 PL 的表述更关键。
approaching 与 departing 的差异:图 4、表 2 以及"交叉点"
在确认 Proposed 相对四个标准模型更贴合数据之后,论文进一步把注意力集中到 approaching 与 departing 两阶段的差异,提出两个问题:差异是否显著?是否随相对速度变化?
图 4:Proposed 模型在 moving in / moving away 两阶段的对比(含外推段)
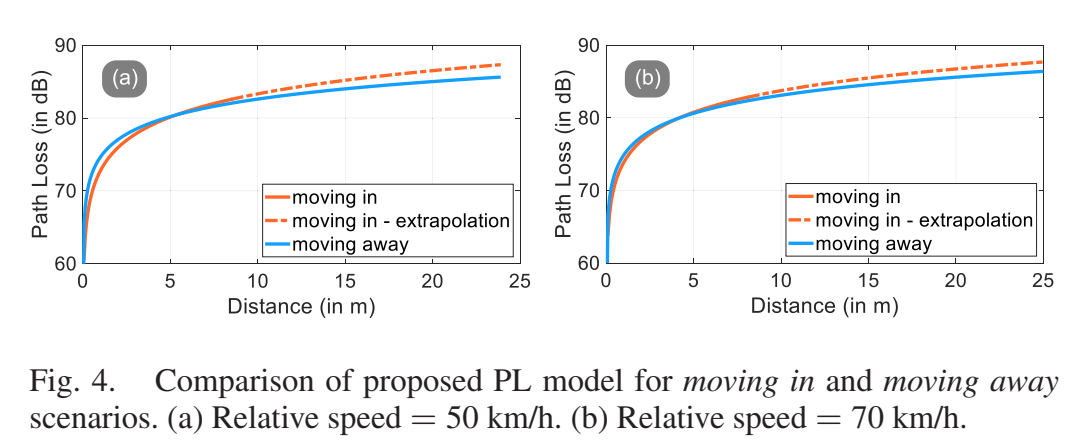
图 4 给出的现象可概括为:当 Tx-Rx 距离较近(约小于 5 m)时,departing(远离阶段)的 PL 略高;随着距离增大,趋势发生反转,即 approaching 阶段的 PL 更高。两条曲线存在一个"交叉点"(crossover distance),且交叉点位置随速度变化:相对速度 70 km/h 时交叉点约 4.12 m;相对速度 50 km/h 时约 5.2 m。论文同时指出:两阶段 PL 的最大差值不超过 2 dB,说明差异虽然系统存在,但幅度并不夸张。
表 2:Proposed 模型在四种工况下的参数 η1,η2,σ\eta_1,\eta_2,\sigmaη1,η2,σ
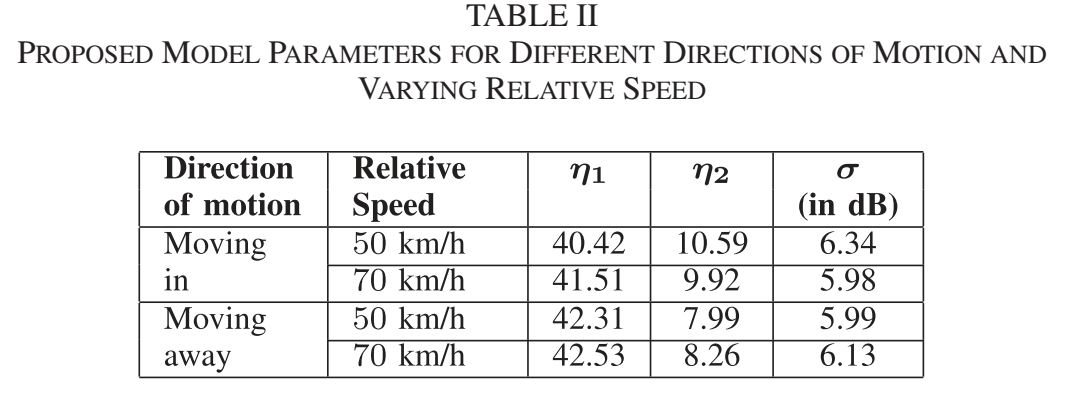
表 2 最直接地揭示了"方向效应强于速度效应"的来源:同一方向下,η1,η2\eta_1,\eta_2η1,η2 在 50 与 70 km/h 两个速度间变化不大;但在不同方向之间,η2\eta_2η2 的变化更明显。数值上,moving in 的 η2\eta_2η2 约在 9.92--10.59,而 moving away 的 η2\eta_2η2 约在 7.99--8.26。由于式 (5) 中距离项是 η2log10(d)\eta_2\log_{10}(d)η2log10(d),η2\eta_2η2 越大,PL 随距离增长越快,这与图 4 的"近距离 departing 略高、远距离 approaching 略高"是一致的:departing 的截距项略大但斜率更小,approaching 的截距略小但斜率更大,两者自然会出现交叉。
论文进一步给出一个工程化简化:即便忽略速度差异,也可以用平均参数近似描述两类方向:moving in 近似 η1≈41,η2≈10\eta_1\approx 41, \eta_2\approx 10η1≈41,η2≈10,moving away 近似 η1≈42,η2≈8\eta_1\approx 42, \eta_2\approx 8η1≈42,η2≈8,阴影衰落标准差可近似统一为 σ≈6\sigma\approx 6σ≈6 dB。这意味着在该 LOS 对向交汇场景与 59.6 GHz 条件下,模型区分"方向"比区分"速度"更有收益。
讨论:模型为什么能赢、以及它的适用边界在哪里
Proposed 形式上接近 3GPP,但把关键的截距与距离系数交给数据拟合。其效果之所以明显,至少来自三点:第一,数据来自非常具体的对向交汇场景,标准模型的参数往往来自更通用的城市宏/微蜂窝统计,直接套用会产生系统偏差;第二,59.6 GHz 下近距离区域更容易出现多径干涉与车体散射主导的非理想自由空间行为,导致"有效斜率"偏离传统假设,固定斜率的模型很难同时兼顾近距离与中距离;第三,approaching / departing 的几何差异虽然不大但可观测,允许模型在两阶段分别拟合 η1,η2\eta_1,\eta_2η1,η2 后会自然得到更小的 RMSE。
与此同时,论文也隐含了它的适用边界:测量为 LOS、场地相对开阔、无其他车辆干扰、仅在 59.6 GHz 单频点、车辆与天线安装方式固定、试验次数有限(尤其 70 km/h 仅 2 次)。因此更严格地说,这是一个"特定频段 + 特定对向交汇 + 车顶侧边安装 + LOS"条件下的测量标定模型,若迁移到遮挡更强、车流更复杂或天线布设不同的场景,参数需要重新校准。
总结:论文给出的可复用信息
这篇工作最"可直接搬运"的结论并不复杂:在 59.6 GHz 的对向交汇 V2V LOS 场景中,用
PL(d)=η1+18.2log10(fc)+η2log10(d)+Xσ PL(d)=\eta_1+18.2\log_{10}(f_c)+\eta_2\log_{10}(d)+X_{\sigma} PL(d)=η1+18.2log10(fc)+η2log10(d)+Xσ
并分别针对 approaching 与 departing 两阶段拟合 η1,η2\eta_1,\eta_2η1,η2,能够在 RMSE 与复合指标上稳定优于 FI/CI/ABG/3GPP;而在该实验条件下,"运动方向(approaching/ departing)对参数的影响"大于"相对速度(50/70 km/h)的影响"。进一步地,这种参数结构还能解释图 4 的交叉点现象,并可提供一个速度无关的平均化工程模型。
附录:补全与加深数学推导
A.1 从 Friis 方程推导 FSPLFSPLFSPL 与 CI 模型
自由空间中,Friis 传输公式写为
Pr=PtGtGr(λ4πd)2, P_r=P_t G_t G_r\left(\frac{\lambda}{4\pi d}\right)^2, Pr=PtGtGr(4πdλ)2,
其中 λ=c/f\lambda=c/fλ=c/f,ddd 为 Tx-Rx 距离。将两边取 10log 得到 dB 域关系:
Pr(dBm)=Pt(dBm)+Gt(dB)+Gr(dB)−20log10(4πdλ). P_r(\mathrm{dBm}) = P_t(\mathrm{dBm}) + G_t(\mathrm{dB}) + G_r(\mathrm{dB})- 20\log_{10}\left(\frac{4\pi d}{\lambda}\right). Pr(dBm)=Pt(dBm)+Gt(dB)+Gr(dB)−20log10(λ4πd).
把"路径损耗"定义为发射等效全向辐射功率(EIRP)与接收功率之间的差(忽略系统损耗项时):
PL(d)=Pt+Gt+Gr−Pr=20log10(4πdλ). PL(d)=P_t+G_t+G_r-P_r =20\log_{10}\left(\frac{4\pi d}{\lambda}\right). PL(d)=Pt+Gt+Gr−Pr=20log10(λ4πd).
代入 λ=c/f\lambda=c/fλ=c/f 得
PL(d)=20log10(4πfdc). PL(d)=20\log_{10}\left(\frac{4\pi f d}{c}\right). PL(d)=20log10(c4πfd).
当 d=d0=1d=d_0=1d=d0=1 m 时,自由空间损耗定义为
FSPL(f,d0)=20log10(4πfd0c)=20log10(4πfc). FSPL(f,d_0)=20\log_{10}\left(\frac{4\pi f d_0}{c}\right) =20\log_{10}\left(\frac{4\pi f}{c}\right). FSPL(f,d0)=20log10(c4πfd0)=20log10(c4πf).
于是任意距离可写成"1 m 锚点 + 距离增量"的形式:
PL(f,d)=FSPL(f,1 m)+20log10(d). PL(f,d)=FSPL(f,1\text{ m})+20\log_{10}(d). PL(f,d)=FSPL(f,1 m)+20log10(d).
真实环境中由于反射/散射/地面反射等效应,距离项的系数不再固定为 20,而用 10β10\beta10β 替代,外加对数正态阴影衰落项 XσX_\sigmaXσ,就得到 CI 形式:
PL(f,d)=FSPL(f,1 m)+10βlog10(d)+Xσ, PL(f,d)=FSPL(f,1\text{ m})+10\beta\log_{10}(d)+X_\sigma, PL(f,d)=FSPL(f,1 m)+10βlog10(d)+Xσ,
与论文式 (2) 在 d0=1d_0=1d0=1 时等价。
数值复算:
FSPL(59.6 GHz,1 m)=20log10(4π⋅59.6×1093×108)≈67.95 dB. FSPL(59.6\text{ GHz},1\text{ m}) =20\log_{10}\left(\frac{4\pi\cdot 59.6\times 10^9}{3\times 10^8}\right) \approx 67.95\text{ dB}. FSPL(59.6 GHz,1 m)=20log10(3×1084π⋅59.6×109)≈67.95 dB.
A.2 FI / CI / ABG / Proposed 的最小二乘拟合写法
论文在图 3 中展示了标准模型的"最佳拟合曲线",这意味着其参数是用测量数据估计得到的。把这些模型统一写成线性回归形式,可以直接给出闭式最小二乘解。
设有 nnn 个距离样本 dkd_kdk 与对应测量路径损耗 yk=PLmeas(dk)y_k=PL_{\text{meas}}(d_k)yk=PLmeas(dk),并定义
xk=log10(dk). x_k=\log_{10}(d_k). xk=log10(dk).
FI:α\alphaα 与 β\betaβ 的闭式解
FI 为
yk=α+10βxk+εk. y_k=\alpha+10\beta x_k+\varepsilon_k. yk=α+10βxk+εk.
令参数向量
θ=[α10β],X=[1x11x2⋮⋮1xn],y=[y1y2⋮yn]. \theta= \begin{bmatrix}\alpha\\ 10\beta\end{bmatrix},\quad \mathbf{X}= \begin{bmatrix} 1 & x_1\\ 1 & x_2\\ \vdots & \vdots\\ 1 & x_n \end{bmatrix},\quad \mathbf{y}= \begin{bmatrix} y_1\\y_2\\\vdots\\y_n \end{bmatrix}. θ=[α10β],X= 11⋮1x1x2⋮xn ,y= y1y2⋮yn .
则最小二乘解
θ^=(XTX)−1XTy. \hat{\theta}=(\mathbf{X}^\mathsf{T}\mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\mathbf{y}. θ^=(XTX)−1XTy.
从 θ^\hat{\theta}θ^ 的第二个分量即可得到 β^=θ^2/10\hat{\beta}=\hat{\theta}_2/10β^=θ^2/10。
CI:只拟合 β\betaβ(锚点固定)
CI(取 d0=1d_0=1d0=1)可写为
yk−FSPL(f,1 m)=10βxk+εk. y_k-FSPL(f,1\text{ m})=10\beta x_k+\varepsilon_k. yk−FSPL(f,1 m)=10βxk+εk.
令 yk′=yk−FSPLy'_k=y_k-FSPLyk′=yk−FSPL,则是一元回归(过原点),闭式解为
10β^=∑k=1nxkyk′∑k=1nxk2,β^=110∑xkyk′∑xk2. \widehat{10\beta}=\frac{\sum_{k=1}^n x_k y'k}{\sum{k=1}^n x_k^2}, \quad \hat{\beta}=\frac{1}{10}\frac{\sum x_k y'_k}{\sum x_k^2}. 10β =∑k=1nxk2∑k=1nxkyk′,β^=101∑xk2∑xkyk′.
ABG:多元回归
ABG 为
yk=α+10βlog10(dkd0)+10γlog10(fcf0)+εk. y_k=\alpha+10\beta \log_{10}\Big(\frac{d_k}{d_0}\Big)+10\gamma\log_{10}\Big(\frac{f_c}{f_0}\Big)+\varepsilon_k. yk=α+10βlog10(d0dk)+10γlog10(f0fc)+εk.
在单频点实验里,log10(fc/f0)\log_{10}(f_c/f_0)log10(fc/f0) 是常数,因此 10γlog10(fc/f0)10\gamma\log_{10}(f_c/f_0)10γlog10(fc/f0) 与 α\alphaα 在统计上会强耦合;若做多频联合拟合,则该项可提供频率维度的信息。一般写成
yk=α+10βxd,k+10γxf+εk, y_k=\alpha + 10\beta x_{d,k}+10\gamma x_f+\varepsilon_k, yk=α+10βxd,k+10γxf+εk,
其中 xd,k=log10(dk/d0)x_{d,k}=\log_{10}(d_k/d_0)xd,k=log10(dk/d0), xf=log10(fc/f0)x_f=\log_{10}(f_c/f_0)xf=log10(fc/f0)。同样可用矩阵法最小二乘求解。
Proposed:单频点下本质是"截距 + log10(d)\log_{10}(d)log10(d) 斜率"的回归
Proposed 为
yk=η1+18.2log10(fc)+η2xk+εk. y_k=\eta_1+18.2\log_{10}(f_c)+\eta_2 x_k+\varepsilon_k. yk=η1+18.2log10(fc)+η2xk+εk.
把频率常数项并入新的截距
θ0=η1+18.2log10(fc), \theta_0=\eta_1+18.2\log_{10}(f_c), θ0=η1+18.2log10(fc),
则模型简化为
yk=θ0+η2xk+εk, y_k=\theta_0+\eta_2 x_k+\varepsilon_k, yk=θ0+η2xk+εk,
与 FI 的回归结构相同,因此
θ\^0η\^2\]=(XTX)−1XTy,η\^1=θ\^0−18.2log10(fc). \\begin{bmatrix}\\hat{\\theta}_0\\\\ \\hat{\\eta}_2\\end{bmatrix} =(\\mathbf{X}\^\\mathsf{T}\\mathbf{X})\^{-1}\\mathbf{X}\^\\mathsf{T}\\mathbf{y}, \\quad \\hat{\\eta}_1=\\hat{\\theta}_0-18.2\\log_{10}(f_c). \[θ\^0η\^2\]=(XTX)−1XTy,η\^1=θ\^0−18.2log10(fc). 这给出了一个很实用的工程结论:在固定频点下,Proposed 参数拟合可直接用"线性回归对 log10(d)\\log_{10}(d)log10(d) 拟合"完成,之后再把 η1\\eta_1η1 从截距中减去频率常数即可。 *** ** * ** *** ### A.3 阴影衰落标准差 σ\\sigmaσ 的估计与含义 在 log-distance 类模型里,通常假设残差(测量 PL 与拟合 PL 的差)满足零均值高斯分布,即 εk=yk−y\^k∼N(0,σ2). \\varepsilon_k=y_k-\\hat{y}_k\\sim \\mathcal{N}(0,\\sigma\^2). εk=yk−y\^k∼N(0,σ2). 于是 σ\\sigmaσ 既可以按样本 PL 的离散度估计,也可以更严格地按残差估计: σ\^=1n−1∑k=1n(εk−εˉ)2. \\hat{\\sigma} =\\sqrt{\\frac{1}{n-1}\\sum_{k=1}\^{n}\\left(\\varepsilon_k-\\bar{\\varepsilon}\\right)\^2}. σ\^=n−11k=1∑n(εk−εˉ)2 . 在理想拟合中 εˉ\\bar{\\varepsilon}εˉ 接近 0,因此常见简化是 σ\^≈1n−1∑k=1nεk2. \\hat{\\sigma}\\approx \\sqrt{\\frac{1}{n-1}\\sum_{k=1}\^{n}\\varepsilon_k\^2}. σ\^≈n−11k=1∑nεk2 . 表 2 中 σ\\sigmaσ 约为 6 dB,意味着在该 LOS 对向交汇场景下,即便采用最佳拟合模型,PL 仍会围绕均值曲线产生约 6 dB 的大尺度起伏,这对链路预算与可靠性分析是直接有效的信息。 *** ** * ** *** ### A.4 GRG 与 PCC 的"相似度化"与复合指标的可复算形式 论文在正文只写出了复合指标 (6)--(8) 的框架,而把 GRG 与 PCC 的具体细节留给参考文献。为便于复算,这里给出标准写法。 #### 灰关联度(Grey Relational Grade, GRG)的常见计算 给定参考序列(测量)x0(k)x_0(k)x0(k) 与对比序列(模型)xi(k)x_i(k)xi(k),定义差分 Δi(k)=∣x0(k)−xi(k)∣. \\Delta_i(k)=\|x_0(k)-x_i(k)\|. Δi(k)=∣x0(k)−xi(k)∣. 在所有 i,ki,ki,k 上取 Δmin=mini,kΔi(k),Δmax=maxi,kΔi(k). \\Delta_{\\min}=\\min_{i,k}\\Delta_i(k),\\quad \\Delta_{\\max}=\\max_{i,k}\\Delta_i(k). Δmin=i,kminΔi(k),Δmax=i,kmaxΔi(k). 灰关联关联系数(Grey Relational Coefficient)定义为 ξi(k)=Δmin+ζΔmaxΔi(k)+ζΔmax, \\xi_i(k)=\\frac{\\Delta_{\\min}+\\zeta \\Delta_{\\max}}{\\Delta_i(k)+\\zeta\\Delta_{\\max}}, ξi(k)=Δi(k)+ζΔmaxΔmin+ζΔmax, 其中 ζ∈(0,1)\\zeta\\in(0,1)ζ∈(0,1) 是分辨系数,常用 ζ=0.5\\zeta=0.5ζ=0.5。则灰关联度(对 kkk 平均)为 ρgrg=1n∑k=1nξi(k),ρgrg∈(0,1\]. \\rho_{\\mathrm{grg}}=\\frac{1}{n}\\sum_{k=1}\^{n}\\xi_i(k), \\qquad \\rho_{\\mathrm{grg}}\\in(0,1\]. ρgrg=n1k=1∑nξi(k),ρgrg∈(0,1\]. ρgrg\\rho_{\\mathrm{grg}}ρgrg 越接近 1,表示两序列越接近。 #### 皮尔逊相关系数 PCC 的相似度化 皮尔逊相关系数 r=∑k(x0(k)−xˉ0)(xi(k)−xˉi)∑k(x0(k)−xˉ0)2∑k(xi(k)−xˉi)2,r∈\[−1,1\]. r=\\frac{\\sum_{k}(x_0(k)-\\bar{x}_0)(x_i(k)-\\bar{x}_i)}{\\sqrt{\\sum_{k}(x_0(k)-\\bar{x}_0)\^2}\\sqrt{\\sum_{k}(x_i(k)-\\bar{x}_i)\^2}}, \\quad r\\in\[-1,1\]. r=∑k(x0(k)−xˉ0)2 ∑k(xi(k)−xˉi)2 ∑k(x0(k)−xˉ0)(xi(k)−xˉi),r∈\[−1,1\]. 为了与 GRG 的 \[0,1\]\[0,1\]\[0,1\] 区间一致,常见映射是 ρpcc=1+r2∈\[0,1\]. \\rho_{\\mathrm{pcc}}=\\frac{1+r}{2}\\in\[0,1\]. ρpcc=21+r∈\[0,1\]. 当 r=1r=1r=1(完全正相关)时 ρpcc=1\\rho_{\\mathrm{pcc}}=1ρpcc=1,当 r=−1r=-1r=−1(完全负相关)时 ρpcc=0\\rho_{\\mathrm{pcc}}=0ρpcc=0。 #### MAPE 的"越大越好"改写 论文给出 Pere=1n∑k=1n∣xi(k)−x0(k)∣x0(k), P_{\\mathrm{ere}}=\\frac{1}{n}\\sum_{k=1}\^{n}\\frac{\|x_i(k)-x_0(k)\|}{x_0(k)}, Pere=n1k=1∑nx0(k)∣xi(k)−x0(k)∣, 并定义 ρmape=∣1−Pere∣. \\rho_{\\mathrm{mape}}=\|1-P_{\\mathrm{ere}}\|. ρmape=∣1−Pere∣. 它的直觉是:误差越小,PereP_{\\mathrm{ere}}Pere 越接近 0,则 ρmape\\rho_{\\mathrm{mape}}ρmape 越接近 1,从而与"相似度越大越好"一致。随后用 α=0.1,β=0.9\\alpha=0.1,\\beta=0.9α=0.1,β=0.9 形成 ρgrg−mape=∣αρgrg+βρmape∣,ρpcc−mape=∣αρpcc+βρmape∣. \\rho_{\\mathrm{grg-mape}}=\|\\alpha\\rho_{\\mathrm{grg}}+\\beta\\rho_{\\mathrm{mape}}\|, \\quad \\rho_{\\mathrm{pcc-mape}}=\|\\alpha\\rho_{\\mathrm{pcc}}+\\beta\\rho_{\\mathrm{mape}}\|. ρgrg−mape=∣αρgrg+βρmape∣,ρpcc−mape=∣αρpcc+βρmape∣. 这两式都能直接复算表 1 中对应指标(前提是有原始 PL 序列与模型预测序列)。 *** ** * ** *** ### A.5 图 4 交叉点距离的解析表达,并用表 2 数值验证 论文给出交叉点约 4.12 m(70 km/h)与约 5.2 m(50 km/h),但正文并未把交叉点与参数 η1,η2\\eta_1,\\eta_2η1,η2 的关系写成解析式。实际上,只要从式 (5) 出发就能直接推导。 对同一频点 fcf_cfc 下的 moving in / moving away 两条曲线分别写为 PLin(d)=η1,in+C+η2,inlog10(d), PL_{\\mathrm{in}}(d)=\\eta_{1,\\mathrm{in}}+C+\\eta_{2,\\mathrm{in}}\\log_{10}(d), PLin(d)=η1,in+C+η2,inlog10(d), PLaway(d)=η1,away+C+η2,awaylog10(d), PL_{\\mathrm{away}}(d)=\\eta_{1,\\mathrm{away}}+C+\\eta_{2,\\mathrm{away}}\\log_{10}(d), PLaway(d)=η1,away+C+η2,awaylog10(d), 其中 C=18.2log10(fc)C=18.2\\log_{10}(f_c)C=18.2log10(fc) 为相同常数,因此交叉点由 PLin(d∗)=PLaway(d∗) PL_{\\mathrm{in}}(d\^\\ast)=PL_{\\mathrm{away}}(d\^\\ast) PLin(d∗)=PLaway(d∗) 决定。两边相减并消去 CCC 得 η1,in−η1,away+(η2,in−η2,away)log10(d∗)=0. \\eta_{1,\\mathrm{in}}-\\eta_{1,\\mathrm{away}} +\\left(\\eta_{2,\\mathrm{in}}-\\eta_{2,\\mathrm{away}}\\right)\\log_{10}(d\^\\ast)=0. η1,in−η1,away+(η2,in−η2,away)log10(d∗)=0. 于是 log10(d∗)=η1,away−η1,inη2,in−η2,away,d∗=10η1,away−η1,inη2,in−η2,away. \\log_{10}(d\^\\ast)= \\frac{\\eta_{1,\\mathrm{away}}-\\eta_{1,\\mathrm{in}}}{\\eta_{2,\\mathrm{in}}-\\eta_{2,\\mathrm{away}}}, \\qquad d\^\\ast=10\^{\\frac{\\eta_{1,\\mathrm{away}}-\\eta_{1,\\mathrm{in}}}{\\eta_{2,\\mathrm{in}}-\\eta_{2,\\mathrm{away}}}}. log10(d∗)=η2,in−η2,awayη1,away−η1,in,d∗=10η2,in−η2,awayη1,away−η1,in. 把表 2 数值代入即可复现论文现象: 当相对速度 70,km/h: η1,in=41.51, η2,in=9.92;η1,away=42.53, η2,away=8.26. \\eta_{1,\\mathrm{in}}=41.51,\\ \\eta_{2,\\mathrm{in}}=9.92;\\quad \\eta_{1,\\mathrm{away}}=42.53,\\ \\eta_{2,\\mathrm{away}}=8.26. η1,in=41.51, η2,in=9.92;η1,away=42.53, η2,away=8.26. 因此 d∗=1042.53−41.519.92−8.26=101.021.66≈100.614≈4.12 m, d\^\\ast=10\^{\\frac{42.53-41.51}{9.92-8.26}} =10\^{\\frac{1.02}{1.66}} \\approx 10\^{0.614} \\approx 4.12\~\\text{m}, d∗=109.92−8.2642.53−41.51=101.661.02≈100.614≈4.12 m, 与论文给出的 4.12 m 完全一致。 当相对速度 50,km/h: η1,in=40.42, η2,in=10.59;η1,away=42.31, η2,away=7.99, \\eta_{1,\\mathrm{in}}=40.42,\\ \\eta_{2,\\mathrm{in}}=10.59;\\quad \\eta_{1,\\mathrm{away}}=42.31,\\ \\eta_{2,\\mathrm{away}}=7.99, η1,in=40.42, η2,in=10.59;η1,away=42.31, η2,away=7.99, 则 d∗=1042.31−40.4210.59−7.99=101.892.60≈100.727≈5.33 m. d\^\\ast=10\^{\\frac{42.31-40.42}{10.59-7.99}} =10\^{\\frac{1.89}{2.60}} \\approx 10\^{0.727} \\approx 5.33\~\\text{m}. d∗=1010.59−7.9942.31−40.42=102.601.89≈100.727≈5.33 m. 论文正文描述约 5.2 m,而由表 2 四舍五入后的参数代入得到约 5.33 m,两者在"参数取整/拟合取样细节"引入的误差范围内一致。这一推导把图 4 的现象与表 2 的参数联系成了可复算的解析关系,也说明 Proposed 模型不仅能拟合数据,还能用参数差异解释 approaching/ departing 的曲线交叉。