leetcode 2147

sin_hielo2025-12-15 15:09

2147: 分割长廊的方案数

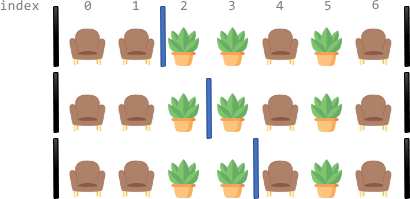
在示例 1 中，我们可以在第 2 个座位和第 3 个座位之间的任意空隙放置一个屏风，空隙个数为两个座位的下标之差 4−1=3。

如果座位更多，例如 corridor="SSPPSSPPPSS"，我们可以：

在第 2 个座位和第 3 个座位之间的任意空隙放置一个屏风，空隙个数为两个座位的下标之差 4−1=3。
在第 4 个座位和第 5 个座位之间的任意空隙放置一个屏风，空隙个数为两个座位的下标之差 9−5=4。
这两个屏风如何放置互相独立，根据乘法原理，划分走廊的方案数为 3⋅4=12。

一般地，对于第 3,5,7,... 个座位，可以在其到其左侧最近座位之间的任意空隙放置一个屏风，空隙个数为两个座位的下标之差。总的方案数为每个屏风的放法之积。

不合法的情况：

1.没有座位。不满足题目「每一段内都恰好有两个座位」的要求。

2.一共有奇数个座位。这会导致某一段只有一个座位，不满足要求。

复制代码

class Solution {
public:
    int numberOfWays(string corridor) {
        constexpr int MOD=1'000'000'007;
        long long ans=1;
        int cnt_s=0,last_s=0;
        for(int i=0;i<corridor.size();i++){
            if(corridor[i]=='S'){
                cnt_s++;
                if(cnt_s>=3 && cnt_s%2==1) ans=ans*(i-last_s)%MOD;
                last_s=i;
            }
        }
        if(cnt_s==0 || cnt_s%2==1) return 0;
        return ans;
    }
};