2015 年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
这一次,小明要帮助 nn 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
现在,这 nn 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为(x1,y1x1,y1) 高度为 h1h1 的村庄与坐标为 (x2,y2x2,y2) 高度为 h2h2 的村庄之间连接的费用为
(x1−x2)2+(y1−y2)2+(h1−h2)2(x1−x2)2+(y1−y2)2+(h1−h2)2
高度的计算方式与横纵坐标的计算方式不同。
由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 nn 个村庄都通电。
输入描述
输入的第一行包含一个整数 nn ,表示村庄的数量。
接下来 nn 行,每个三个整数 x,y,hx,y,h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
其中,1≤n≤1000,0≤x,y,h≤100001≤n≤1000,0≤x,y,h≤10000。
输出描述
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
输入输出样例
示例
输入
4
1 1 3
9 9 7
8 8 6
4 5 4输出
17.41这道题本质就是求最小生成树,这里我们用到Prim算法:
核心思想:
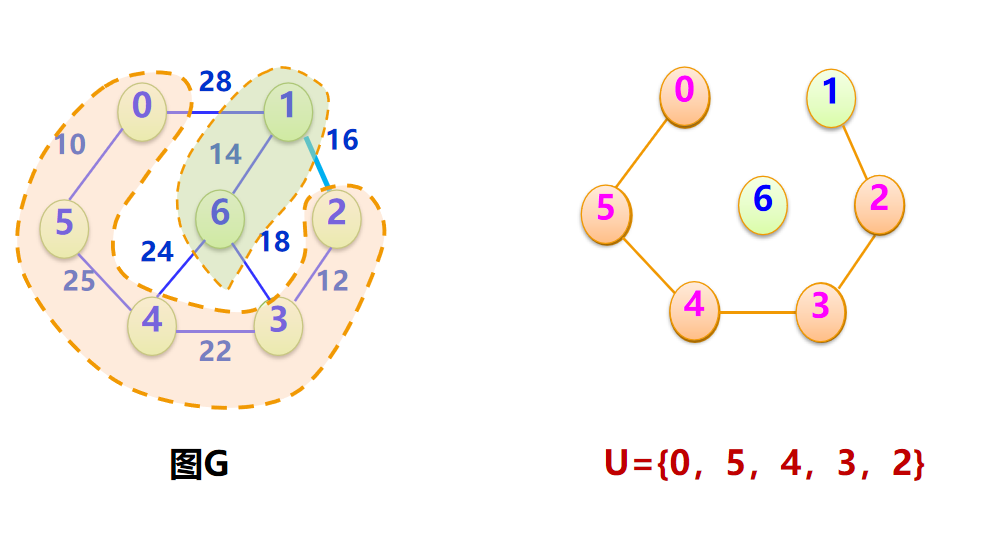
从任意一个起点顶点出发,每次选择当前已连接顶点集合 到未连接顶点集合中权值最小的边,将该未连接顶点纳入已连接集合;重复此过程,直到所有顶点都被纳入,最终形成的边集合即为最小生成树。
Prim算法示例演示(起点0)
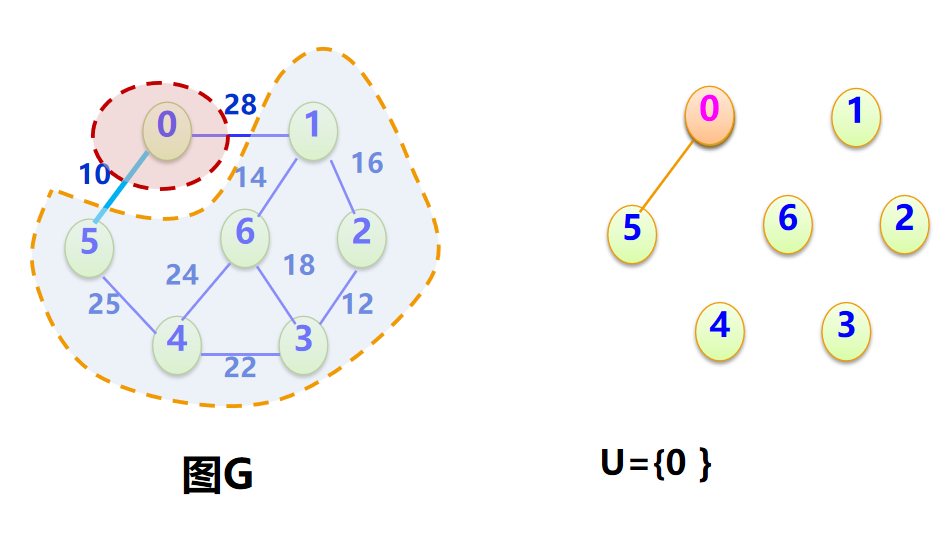
↓
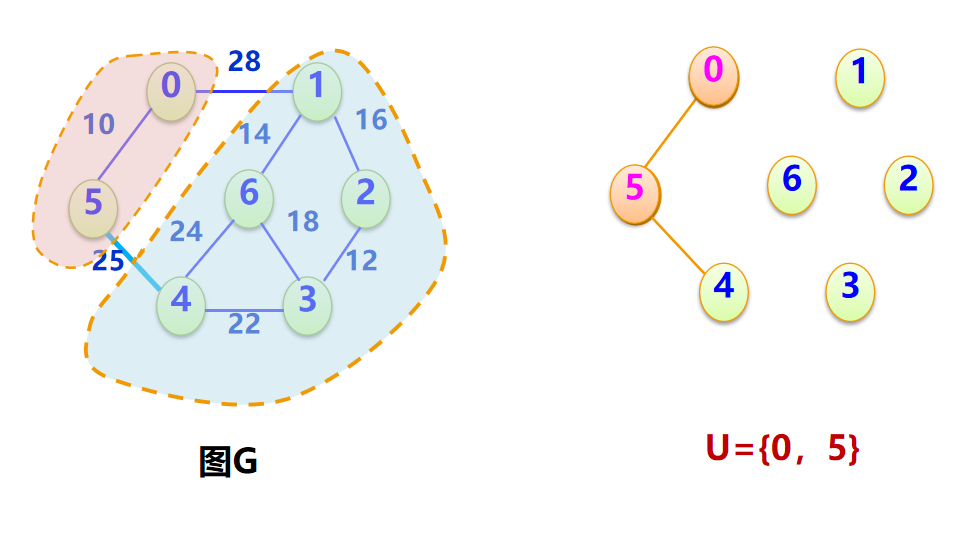
↓
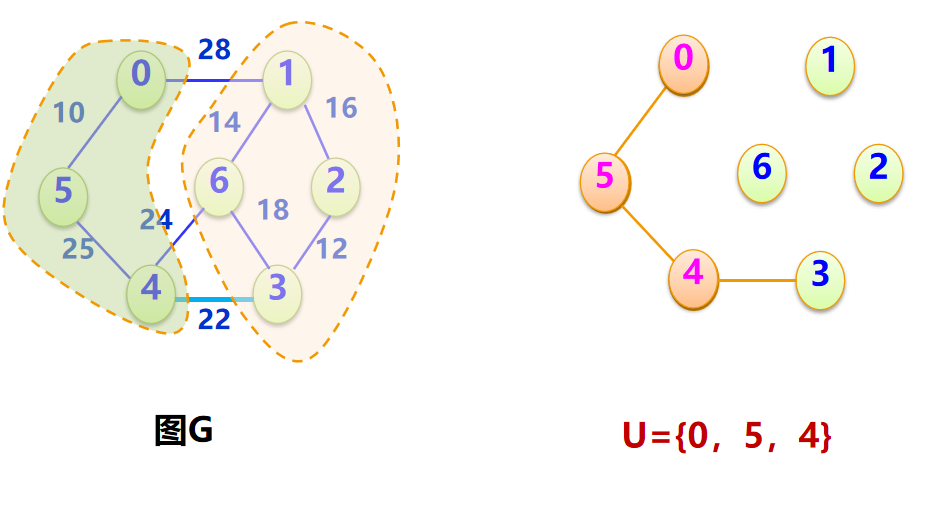
↓
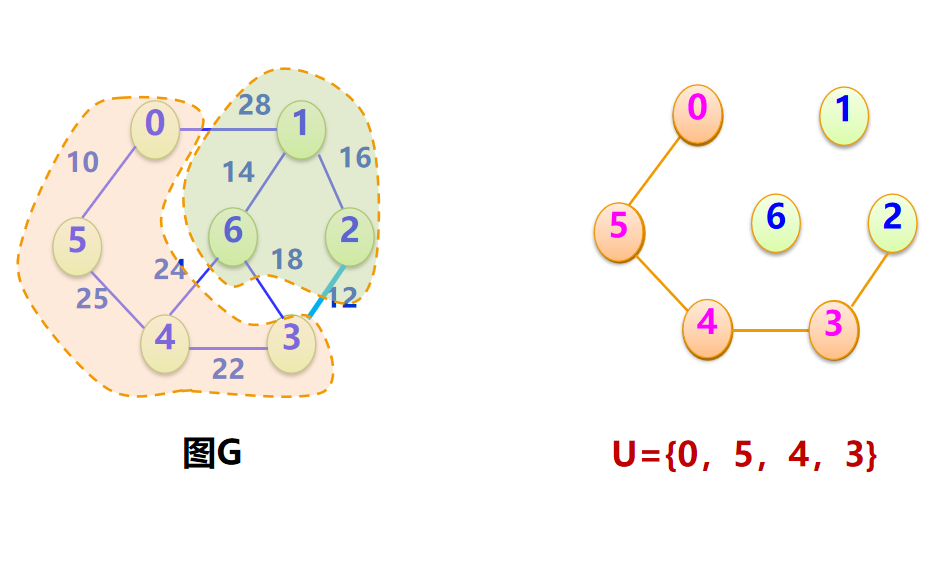
↓
↓

java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int cun[][] = new int[n][3];//村庄信息
for (int i = 0; i < n; i++) {
String s[] = br.readLine().split(" ");
cun[i][0] = Integer.parseInt(s[0]);
cun[i][1] = Integer.parseInt(s[1]);
cun[i][2] = Integer.parseInt(s[2]);
}
double minleng = 0;//最短总长度
double juli[][] = new double[n][n];//各个村庄之间的距离
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
juli[i][j] = Double.MAX_VALUE;
} else {
juli[i][j] = Math.sqrt(Math.pow(cun[i][0] - cun[j][0], 2) + Math.pow(cun[i][1] - cun[j][1], 2)) + Math.pow(cun[i][2] - cun[j][2], 2);
}
}
}
//Prim算法初始化
boolean intree[] = new boolean[n];//村庄是否加入当前的生成树中
intree[0] = true;//初始化村庄1
double dist[] = new double[n]; // 记录每个顶点到当前生成树的最小距离
Arrays.fill(dist, Double.MAX_VALUE);
dist[0] = 0;
for (int i = 1; i < n; i++) {
dist[i] = juli[0][i];
}
//Prim算法
for (int i = 1; i < n; i++) {
int u = -1;// 找到"未访问且距离当前生成树最近"的顶点u
double mindist = Double.MAX_VALUE;//u到当前生成树的最小距离
for (int j = 0; j < n; j++) {
if (!intree[j] && dist[j] < mindist) {
mindist = dist[j];
u = j;
}
}
minleng += mindist;
intree[u] = true;
// 更新其他未访问顶点到生成树的最小距离
for (int j = 0; j < n; j++) {
if (!intree[j] && juli[u][j] < dist[j]) {
dist[j] = juli[u][j];
}
}
}
String result = String.format("%.2f", minleng);
System.out.println(result);
}
}