数据结构知识整理——复杂度的计算

复杂度（Complexity）通常指算法或程序在运行过程中对计算资源的消耗程度，主要分为时间复杂度和空间复杂度两类。它用于衡量算法效率，帮助开发者评估不同算法在输入规模增长时的性能表现。

时间复杂度的计算

时间复杂度描述算法执行所需时间与输入规模的关系。常用大O符号（O-notation）表示，一般不必要计算出精确的操作重复次数，只要计算出对应的数量级即可。

数量级的排序如下：

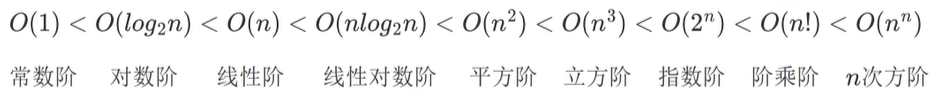
加法规则：多项相加，保留最高，系数化
乘法规则：多项相乘，全部保留
加法乘法混合规则：先小括号，再乘法，后加法

常见场景

O(1) - 常数时间复杂度

python 复制代码

def get_first_element(arr):
    return arr[0]  # 直接访问数组第一个元素

O(log n) - 对数时间复杂度

python 复制代码

def binary_search(arr, target):
    left, right = 0, len(arr)-1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

O(n) - 线性时间复杂度

python 复制代码

def find_max(arr):
    max_val = arr[0]
    for num in arr:  # 遍历整个数组
        if num > max_val:
            max_val = num
    return max_val

O(n log2 n) - 线性对数时间复杂度

python 复制代码

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])  # O(log n) 层递归
    right = merge_sort(arr[mid:])
    
    # 合并过程是 O(n)
    return merge(left, right)

O(n²) - 平方时间复杂度

python 复制代码

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):  # 外层循环
        for j in range(0, n-i-1):  # 内层循环
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

O(2ⁿ) - 指数时间复杂度

python 复制代码

def fibonacci_recursive(n):
    if n <= 1:
        return n
    return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

O(n!) - 阶乘时间复杂度

python 复制代码

def generate_permutations(arr, start=0, result=None):
    if result is None:
        result = []
    if start == len(arr):
        result.append(arr.copy())
        return
    
    for i in range(start, len(arr)):
        arr[start], arr[i] = arr[i], arr[start]
        generate_permutations(arr, start+1, result)
        arr[start], arr[i] = arr[i], arr[start]
    
    return result

空间复杂度的计算

空间复杂度用于衡量算法在运行过程中临时占用存储空间的大小，可以理解为创建了多少变量。

常见场景

**O(1)：**仅使用固定数量的变量，如交换两个数的值

复制代码

a, b = b, a

**O(n)：**需要与输入规模线性相关的空间，如生成长度为 n 的数组

python 复制代码

array = [0] * n  # 占用 n 个存储单元

**O(n^2)：**常见于二维数据结构

python 复制代码

matrix = [[0] * n for _ in range(n)]  # 空间与 n² 成正比

渐进符号

大O符号（O）

大O符号表示算法的最坏情况时间复杂度，即上界。

如果一个函数g(n)，有O(g(n)) = f(n)，则存在正常数c、n0，使得所有nn0，有0f(n)cg(n)。

大Ω符号（Ω）

大Ω符号表示算法的最好情况时间复杂度，即下界。

如果一个函数g(n)，有Ω(g(n)) = f(n)，则存在正常数c、n0，使得所有nn0，有0cg(n)f(n)。

大Θ符号（Θ）

大Θ符号表示算法的紧确界，即同时包含上界和下界。

如果一个函数g(n)，有Θ(g(n)) = f(n)，则存在正常数c1、c2、n0，使得所有nn0，有0c1g(n)f(n)c2g(n)。

递归方法的复杂度计算

每次递归的时间复杂度不变时

计算方式：递归的次数*每次递归的时间复杂度

例如：

python 复制代码

def fn(n):
    i = 1;
    if n == 1 return 1;
    return n*fn(n/2)

递归的次数：2^x = n → x = log2 n，所以时间复杂度为O(log2 n)；

每次递归的复杂度：O(1)；

所以整个公式的复杂度为O(1)*O(log2 n) = O(log2 n)

每次递归时时间复杂度改变时

计算方式：将所有的递归时间复杂度相加

例如：

python 复制代码

def fn(n):
    arr = [i for i in range(size)];
    i = 1
    while i<=n:
        print("循环结束")
    return n*fn(n-1)

第一次迭代： n

第二次迭代：n-1

第三次迭代：n-2

第n次迭代：1

总次数：n(n-1)/2 = (n^2)/2 - n/2

所以复杂度为O(n^2)

主方法求递归式的复杂度

公式

主方法也称为主定理，给出了求解以下形式的递归式的快速方法。

T(n) = aT(n/b) + f(n)

其中：

a ≥ 1（子问题个数）
b > 1（分割比例）
f(n) 是渐进正函数

各种情况

情况1：叶子层占主导

条件：f(n) = O(n^(log_b a - ε))，其中 ε > 0

结论：T(n) = Θ(n^(log_b a))

示例：T(n) = 8T(n/2) + 1000n²

a=8, b=2, log_b a = log₂8 = 3
f(n) = 1000n² = O(n²)
比较：n² vs n³，f(n) = O(n^(3-ε)) 对 ε=1
属于情况1，T(n) = Θ(n³)

情况2：各层均匀分布

条件：f(n) = Θ(n^(log_b a) * logᵏ n)，其中 k ≥ 0

结论：T(n) = Θ(n^(log_b a) * log^(k+1) n)

特殊情况：当 k=0 时，f(n) = Θ(n^(log_b a))，则 T(n) = Θ(n^(log_b a) * log n)

示例1：归并排序 T(n) = 2T(n/2) + Θ(n)

a=2, b=2, log_b a = log₂2 = 1
f(n) = Θ(n) = Θ(n¹) = Θ(n^(log_b a))
属于情况2（k=0），T(n) = Θ(n log n)

示例2：T(n) = 2T(n/2) + Θ(n log n)

a=2, b=2, log_b a = 1
f(n) = Θ(n log n) = Θ(n¹ * log¹ n)
属于情况2（k=1），T(n) = Θ(n log² n)

情况3：根层占主导

条件：f(n) = Ω(n^(log_b a + ε))，其中 ε > 0，且满足正则条件 a·f(n/b) ≤ c·f(n)（c<1）

结论：T(n) = Θ(f(n))

示例：T(n) = 2T(n/2) + Θ(n²)

a=2, b=2, log_b a = 1
f(n) = Θ(n²) = Ω(n^(1+ε)) 对 ε=1
检查正则条件：2f(n/2) = 2(n/2)² = n²/2 ≤ c·n² 对 c=1/2
属于情况3，T(n) = Θ(n²)

例题

答案：A