Conv1d(一维卷积)深度学习学习笔记
学习目标:彻底理解一维卷积的工作原理、维度变化规律、以及为什么它能有效提取时序特征
1. 问题动机与直觉理解
1.1 为什么需要 Conv1d?
想象你正在分析一段语音信号、股票价格序列、或者传感器数据流。这些数据有一个共同特点:时间维度上存在局部模式。
举个例子:
- 语音识别:某个音素的发音可能持续 20-50ms,我们需要捕捉这个局部时间窗口内的特征
- 心电图分析:一个心跳的 QRS 波群跨越约 0.06-0.10 秒,局部波形形态决定了是否异常
- 文本情感分析:连续的几个词(如"not bad")组合在一起才能表达完整含义
核心痛点:全连接层(Fully Connected)会忽略时间上的局部相关性,参数量巨大且无法共享模式。
Conv1d 的解决方案:用一个小窗口(kernel)在时间轴上滑动,提取局部特征,并且窗口权重共享。
1.2 与 Conv2d 的类比
如果你理解了图像的 Conv2d:
- Conv2d:在二维空间(高×宽)上滑动卷积核
- Conv1d:在一维时间轴上滑动卷积核
核心思想完全一致:局部感知 + 权重共享。
2. 核心思想与概念拆解
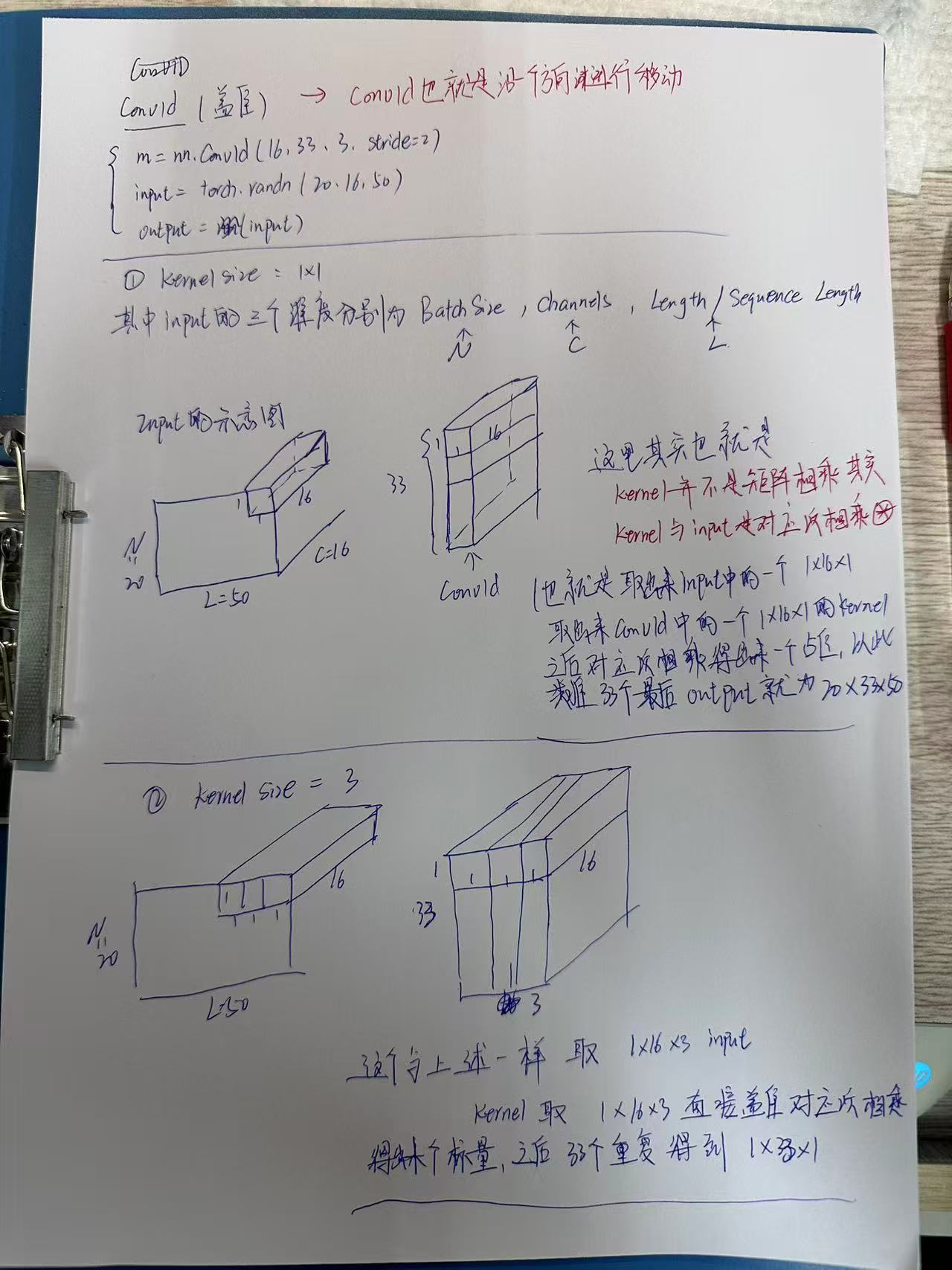
2.1 卷积的本质:不是矩阵乘法!
重要认知:卷积 ≠ 矩阵乘法
卷积的运算步骤:
- 对应位置相乘(Element-wise Multiply)
- 求和(Sum)
用一个类比:卷积核像一个"模板印章",盖在数据上,看看匹配度有多高。
数据块: [1, 2, 3]
卷积核: [0.5, 1, 0.5]
↓
对应相乘: [0.5, 2, 1.5]
↓
求和: 4.0 ← 这就是一个输出值2.2 三个关键维度
在 Conv1d 中,数据有三个维度:
- Batch Size (N):批次大小,一次处理多少条序列
- Channels ©:通道数,每个时间点有多少个特征
- Length (L):序列长度,时间轴上有多少个点
输入形状 :(N, C_in, L_in)
例如:(32, 16, 100) = 32条序列,每条有16个通道,长度为100
输出形状 :(N, C_out, L_out)
例如:(32, 33, 98) = 32条序列,输出33个通道,长度变为98
3. 数学建模与理论基础
3.1 形式化定义
对于 nn.Conv1d(in_channels, out_channels, kernel_size):
卷积核张量的形状 :
Weight∈RCout×Cin×K \text{Weight} \in \mathbb{R}^{C_{\text{out}} \times C_{\text{in}} \times K} Weight∈RCout×Cin×K
其中:
- CoutC_{\text{out}}Cout:输出通道数(有多少个过滤器)
- CinC_{\text{in}}Cin:输入通道数(每个过滤器的深度)
- KKK:卷积核大小(时间维度上的窗口大小)
单个输出值的计算:
对于第 jjj 个输出通道、第 ttt 个时间位置:
y[j,t]=∑i=0Cin−1∑k=0K−1x[i,t+k]⋅w[j,i,k]+b[j] y[j, t] = \sum_{i=0}^{C_{\text{in}}-1} \sum_{k=0}^{K-1} x[i, t+k] \cdot w[j, i, k] + b[j] y[j,t]=i=0∑Cin−1k=0∑K−1x[i,t+k]⋅w[j,i,k]+b[j]
解读:
- 遍历所有输入通道 iii
- 遍历卷积核的每个时间位置 kkk
- 对应位置相乘后求和
- 加上偏置项 b[j]b[j]b[j]
3.2 输出长度计算公式
Lout=⌊Lin+2×padding−dilation×(kernel_size−1)−1stride⌋+1 L_{\text{out}} = \left\lfloor \frac{L_{\text{in}} + 2 \times \text{padding} - \text{dilation} \times (\text{kernel\_size} - 1) - 1}{\text{stride}} \right\rfloor + 1 Lout=⌊strideLin+2×padding−dilation×(kernel_size−1)−1⌋+1
常见情况 (无 dilation、padding=0、stride=1):
Lout=Lin−kernel_size+1 L_{\text{out}} = L_{\text{in}} - \text{kernel\_size} + 1 Lout=Lin−kernel_size+1
为什么长度会减少?
想象一个长度为 5 的序列用大小为 3 的卷积核滑动:
序列: [1, 2, 3, 4, 5]
└─┬─┘ 第1个位置 → 输出[0]
└─┬─┘ 第2个位置 → 输出[1]
└─┬─┘ 第3个位置 → 输出[2]只能滑动 3 次,所以输出长度 = 5 - 3 + 1 = 3
4. 标准卷积的完整运算过程("全家桶"式)
4.1 实例剖析:nn.Conv1d(16, 33, 3)
参数含义:
in_channels=16:输入有 16 个通道out_channels=33:输出有 33 个通道kernel_size=3:卷积核大小为 3
卷积核的实际形状 :
Weight∈R33×16×3 \text{Weight} \in \mathbb{R}^{33 \times 16 \times 3} Weight∈R33×16×3
即:(Output_Channels, Input_Channels, Kernel_Size)
解读 :我们有 33 个过滤器 ,每一个过滤器都是一个 16×316 \times 316×3 的"立体块"。
4.2 逐步运算过程
假设输入数据:x.shape = (1, 16, 100)(batch=1, 16通道, 长度100)
Step 1: 取块
从输入的第 0 个位置开始,取出一个 16×316 \times 316×3 的数据块:
x[:, :, 0:3] # shape: (16, 3)这是一个矩阵,包含:
- 16 个通道
- 3 个时间步
- 总共 16 × 3 = 48 个数字
Step 2: 一步计算(对应相乘 + 求和)
取第 1 个过滤器 (它也是 16×316 \times 316×3 的矩阵):
filter_1 = weight[0, :, :] # shape: (16, 3)对应位置相乘并全部加起来:
output[0, 0] = (x[:, :, 0:3] * filter_1).sum()这就像两个矩阵"叠在一起",对应位置相乘:
数据块: 过滤器:
┌─────────┐ ┌─────────┐
│ 1 2 3 │ × │ a b c │
│ 4 5 6 │ │ d e f │
│ ... │ │ ... │ (16行 × 3列)
└─────────┘ └─────────┘
↓
1×a + 2×b + 3×c + 4×d + 5×e + 6×f + ... (共48项)
↓
一个数字 → output[0, 0]Step 3: 重复 33 次
我们有 33 个过滤器,所以重复做 33 次,得到 33 个数字:
python
for j in range(33):
filter_j = weight[j, :, :] # 第 j 个过滤器
output[0, j, 0] = (x[:, :, 0:3] * filter_j).sum() + bias[j]这 33 个数字就是输出的第 0 个时间步的 33 个通道。
Step 4: 滑动卷积核
卷积核向右滑动一步(stride=1),从位置 1 开始:
x[:, :, 1:4] # shape: (16, 3)重复 Step 2 和 Step 3,得到输出的第 1 个时间步。
总滑动次数 (无 padding):
Lout=100−3+1=98 L_{\text{out}} = 100 - 3 + 1 = 98 Lout=100−3+1=98
所以最终输出:(1, 33, 98)
4.3 关键认知
时间特征提取 + 通道融合是纠缠在一起的
每一个输出通道是由:
- 所有 16 个输入通道
- 在 3 个时间步内
- 按特定权重组合而成
每个过滤器有自己独特的:
- 时间提取方式:在 3 个时间步内如何加权
- 通道组合方式:如何融合 16 个输入通道
这就是为什么 Conv1d 既能捕捉时序模式,又能进行通道间的特征交互。
5. 维度变化详解(配合实例)
5.1 基础实例
python
import torch
import torch.nn as nn
# 定义卷积层
conv = nn.Conv1d(in_channels=16, out_channels=33, kernel_size=3)
# 输入数据
x = torch.randn(32, 16, 100) # (batch, channels, length)
print(f"输入形状: {x.shape}")
# 前向传播
y = conv(x)
print(f"输出形状: {y.shape}")
# 卷积核形状
print(f"卷积核形状: {conv.weight.shape}")输出:
输入形状: torch.Size([32, 16, 100])
输出形状: torch.Size([32, 33, 98])
卷积核形状: torch.Size([33, 16, 3])维度变化分析:
| 维度 | 输入 | 输出 | 变化原因 |
|---|---|---|---|
| Batch | 32 | 32 | 不变,每个样本独立处理 |
| Channels | 16 | 33 | 由 out_channels 决定(33个过滤器) |
| Length | 100 | 98 | 100−3+1=98100 - 3 + 1 = 98100−3+1=98 |
5.2 不同参数下的维度变化
实例 1:改变 kernel_size
python
conv = nn.Conv1d(16, 33, kernel_size=5)
y = conv(x) # x.shape = (32, 16, 100)
print(y.shape) # torch.Size([32, 33, 96])计算 :100−5+1=96100 - 5 + 1 = 96100−5+1=96
实例 2:使用 padding
python
conv = nn.Conv1d(16, 33, kernel_size=3, padding=1)
y = conv(x)
print(y.shape) # torch.Size([32, 33, 100])计算 :100+2×1−3+1=100100 + 2 \times 1 - 3 + 1 = 100100+2×1−3+1=100(长度保持不变)
padding 的作用:在序列两端补零,让输出长度不缩短
原始序列: [1, 2, 3, 4, 5]
padding=1: [0, 1, 2, 3, 4, 5, 0]实例 3:使用 stride
python
conv = nn.Conv1d(16, 33, kernel_size=3, stride=2)
y = conv(x)
print(y.shape) # torch.Size([32, 33, 49])计算 :⌊100−32⌋+1=49\lfloor \frac{100 - 3}{2} \rfloor + 1 = 49⌊2100−3⌋+1=49
stride 的作用:卷积核每次滑动的步长,stride=2 表示每次跳两步(下采样)
实例 4:使用 dilation
python
conv = nn.Conv1d(16, 33, kernel_size=3, dilation=2)
y = conv(x)
print(y.shape) # torch.Size([32, 33, 96])计算:
- 有效卷积核大小:2×(3−1)+1=52 \times (3 - 1) + 1 = 52×(3−1)+1=5
- 输出长度:100−5+1=96100 - 5 + 1 = 96100−5+1=96
dilation 的作用:在卷积核元素之间插入空洞,扩大感受野
普通卷积 (dilation=1): [x x x]
空洞卷积 (dilation=2): [x _ x _ x] (看到5个位置的信息)5.3 综合计算公式(记忆版)
Lout=⌊Lin+2P−D(K−1)−1S⌋+1 L_{\text{out}} = \left\lfloor \frac{L_{\text{in}} + 2P - D(K-1) - 1}{S} \right\rfloor + 1 Lout=⌊SLin+2P−D(K−1)−1⌋+1
其中:
- PPP = padding
- DDD = dilation
- KKK = kernel_size
- SSS = stride
记忆技巧:
- padding 增加长度 :+2P+2P+2P
- 卷积核消耗长度 :−D(K−1)-D(K-1)−D(K−1)(有效卷积核大小)
- stride 控制采样 :除以 SSS(向下取整)
6. 代码实现与工程视角
6.1 手动实现 Conv1d(加深理解)
python
import torch
import torch.nn.functional as F
def manual_conv1d(x, weight, bias=None, stride=1, padding=0):
"""
手动实现 Conv1d(仅支持基础参数)
Args:
x: 输入张量 (N, C_in, L_in)
weight: 卷积核 (C_out, C_in, K)
bias: 偏置 (C_out,) 或 None
stride: 步长
padding: 填充
Returns:
y: 输出张量 (N, C_out, L_out)
"""
N, C_in, L_in = x.shape
C_out, _, K = weight.shape
# 1. 填充
if padding > 0:
x = F.pad(x, (padding, padding), mode='constant', value=0)
L_in = x.shape[2]
# 2. 计算输出长度
L_out = (L_in - K) // stride + 1
# 3. 初始化输出
y = torch.zeros(N, C_out, L_out)
# 4. 滑动卷积
for n in range(N): # 遍历batch
for t in range(L_out): # 遍历输出时间步
start = t * stride
x_block = x[n, :, start:start+K] # 取块 (C_in, K)
for j in range(C_out): # 遍历输出通道
# 对应位置相乘 + 求和
y[n, j, t] = (x_block * weight[j]).sum()
if bias is not None:
y[n, j, t] += bias[j]
return y
# 测试
x = torch.randn(2, 3, 10)
conv = nn.Conv1d(3, 5, 3)
y_manual = manual_conv1d(x, conv.weight, conv.bias)
y_torch = conv(x)
print("手动实现与 PyTorch 的差异:", (y_manual - y_torch).abs().max().item())6.2 可视化卷积过程
python
import matplotlib.pyplot as plt
import numpy as np
def visualize_conv1d():
"""可视化 Conv1d 的滑动过程"""
# 输入信号(单通道,便于可视化)
L = 20
x = np.sin(np.linspace(0, 4*np.pi, L)) + np.random.randn(L) * 0.1
# 卷积核(简单的边缘检测器)
kernel = np.array([-1, 0, 1])
K = len(kernel)
# 手动卷积
L_out = L - K + 1
y = np.zeros(L_out)
fig, axes = plt.subplots(3, 3, figsize=(12, 8))
axes = axes.flatten()
for i in range(min(9, L_out)):
ax = axes[i]
# 绘制输入信号
ax.plot(x, 'b-', alpha=0.3, label='Input')
# 高亮当前窗口
start = i
window = x[start:start+K]
ax.plot(range(start, start+K), window, 'ro-', linewidth=2,
label=f'Window at t={i}')
# 计算输出
y[i] = np.sum(window * kernel)
ax.set_title(f'Step {i}: output = {y[i]:.2f}')
ax.set_ylim(-2, 2)
ax.legend(fontsize=8)
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('/mnt/user-data/outputs/conv1d_visualization.png', dpi=150)
plt.close()
return y
output = visualize_conv1d()
print(f"卷积输出长度: {len(output)}")6.3 常见坑与注意事项
坑1:维度顺序错误
python
# ❌ 错误:使用 (batch, length, channels) 格式
x = torch.randn(32, 100, 16)
conv = nn.Conv1d(16, 33, 3)
# y = conv(x) # 报错!
# ✅ 正确:使用 (batch, channels, length) 格式
x = torch.randn(32, 16, 100)
y = conv(x) # 成功原因:PyTorch 的 Conv1d 要求通道维度在第二个位置。
坑2:输入输出通道不匹配
python
# ❌ 错误
x = torch.randn(32, 10, 100) # 10 个输入通道
conv = nn.Conv1d(16, 33, 3) # 期望 16 个输入通道
# y = conv(x) # 报错!
# ✅ 正确
conv = nn.Conv1d(10, 33, 3) # 与输入通道数匹配
y = conv(x)坑3:序列长度小于卷积核
python
x = torch.randn(32, 16, 2) # 长度只有 2
conv = nn.Conv1d(16, 33, 3) # 卷积核大小为 3
# y = conv(x) # 报错:序列太短!
# 解决方案:使用 padding
conv = nn.Conv1d(16, 33, 3, padding=1)
y = conv(x) # 成功,输出长度为 2坑4:忘记 batch 维度
python
# ❌ 错误:只有 (channels, length)
x = torch.randn(16, 100)
# y = conv(x) # 报错!
# ✅ 正确:添加 batch 维度
x = torch.randn(16, 100).unsqueeze(0) # (1, 16, 100)
y = conv(x)6.4 性能优化技巧
技巧1:使用组卷积(Group Convolution)
python
# 标准卷积:参数量 = 64 × 128 × 3 = 24,576
conv_standard = nn.Conv1d(64, 128, 3)
# 组卷积(groups=4):参数量 = 128 × (64/4) × 3 = 6,144
conv_group = nn.Conv1d(64, 128, 3, groups=4)
print(f"标准卷积参数量: {conv_standard.weight.numel()}")
print(f"组卷积参数量: {conv_group.weight.numel()}")原理:将输入通道分成 4 组,每组独立卷积,减少参数量和计算量。
技巧2:深度可分离卷积(Depthwise Separable)
python
class DepthwiseSeparableConv1d(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size):
super().__init__()
# 深度卷积:每个通道独立卷积
self.depthwise = nn.Conv1d(
in_channels, in_channels, kernel_size,
groups=in_channels, padding=kernel_size//2
)
# 逐点卷积:1×1 卷积融合通道
self.pointwise = nn.Conv1d(in_channels, out_channels, 1)
def forward(self, x):
x = self.depthwise(x)
x = self.pointwise(x)
return x
# 比较参数量
standard = nn.Conv1d(64, 128, 3)
separable = DepthwiseSeparableConv1d(64, 128, 3)
print(f"标准卷积: {sum(p.numel() for p in standard.parameters())}")
print(f"深度可分离: {sum(p.numel() for p in separable.parameters())}")技巧3:使用因果卷积(Causal Convolution)
python
class CausalConv1d(nn.Module):
"""因果卷积:保证时间t的输出只依赖于t及之前的输入"""
def __init__(self, in_channels, out_channels, kernel_size, dilation=1):
super().__init__()
self.padding = (kernel_size - 1) * dilation
self.conv = nn.Conv1d(
in_channels, out_channels, kernel_size,
padding=self.padding, dilation=dilation
)
def forward(self, x):
x = self.conv(x)
# 去掉右侧填充,保证因果性
return x[:, :, :-self.padding] if self.padding > 0 else x
# 测试
x = torch.randn(1, 16, 100)
causal_conv = CausalConv1d(16, 32, 3)
y = causal_conv(x)
print(f"输入长度: {x.shape[2]}, 输出长度: {y.shape[2]}")应用场景:时间序列预测、语音生成(不能"看到未来")。
7. 优化方法与训练机制
7.1 梯度反向传播
Conv1d 的梯度计算遵循链式法则:
∂L∂w[j,i,k]=∑n,t∂L∂y[n,j,t]⋅x[n,i,t+k] \frac{\partial \mathcal{L}}{\partial w[j, i, k]} = \sum_{n, t} \frac{\partial \mathcal{L}}{\partial y[n, j, t]} \cdot x[n, i, t+k] ∂w[j,i,k]∂L=n,t∑∂y[n,j,t]∂L⋅x[n,i,t+k]
直觉理解:卷积核的梯度是"输出梯度"与"对应输入块"的卷积。
python
# PyTorch 自动处理梯度
x = torch.randn(32, 16, 100, requires_grad=True)
conv = nn.Conv1d(16, 33, 3)
y = conv(x)
loss = y.sum()
loss.backward()
print(f"卷积核梯度形状: {conv.weight.grad.shape}") # (33, 16, 3)
print(f"输入梯度形状: {x.grad.shape}") # (32, 16, 100)7.2 权重初始化
默认初始化(Kaiming Uniform):
python
conv = nn.Conv1d(16, 33, 3)
# 权重从 Uniform(-sqrt(k), sqrt(k)) 采样
# 其中 k = 1 / (in_channels * kernel_size) = 1 / 48自定义初始化:
python
import torch.nn.init as init
conv = nn.Conv1d(16, 33, 3)
init.xavier_normal_(conv.weight) # Xavier初始化
init.constant_(conv.bias, 0) # 偏置初始化为07.3 批归一化(Batch Normalization)
python
class ConvBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size):
super().__init__()
self.conv = nn.Conv1d(in_channels, out_channels, kernel_size, padding=kernel_size//2)
self.bn = nn.BatchNorm1d(out_channels) # 对每个通道归一化
self.relu = nn.ReLU()
def forward(self, x):
x = self.conv(x)
x = self.bn(x) # 归一化
x = self.relu(x) # 激活
return xBN1d 的作用:
- 加速训练收敛
- 减少对初始化的敏感性
- 轻微正则化效果
8. 实际应用案例
8.1 案例1:文本分类(TextCNN)
python
class TextCNN(nn.Module):
def __init__(self, vocab_size, embed_dim, num_classes):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_dim)
# 多尺度卷积核
self.conv1 = nn.Conv1d(embed_dim, 100, kernel_size=3)
self.conv2 = nn.Conv1d(embed_dim, 100, kernel_size=4)
self.conv3 = nn.Conv1d(embed_dim, 100, kernel_size=5)
self.fc = nn.Linear(300, num_classes)
def forward(self, x):
# x: (batch, seq_len)
x = self.embedding(x) # (batch, seq_len, embed_dim)
x = x.transpose(1, 2) # (batch, embed_dim, seq_len)
# 多尺度特征提取
x1 = F.relu(self.conv1(x)).max(dim=2)[0] # (batch, 100)
x2 = F.relu(self.conv2(x)).max(dim=2)[0]
x3 = F.relu(self.conv3(x)).max(dim=2)[0]
# 拼接并分类
x = torch.cat([x1, x2, x3], dim=1) # (batch, 300)
x = self.fc(x) # (batch, num_classes)
return x关键点:
transpose(1, 2)将 (batch, seq_len, embed_dim) 转为 (batch, embed_dim, seq_len)- 不同 kernel_size 捕捉不同长度的 n-gram 特征
- Max pooling 提取最显著特征
8.2 案例2:时间序列预测(TCN - Temporal Convolutional Network)
python
class TCNBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, dilation):
super().__init__()
padding = (kernel_size - 1) * dilation # 因果填充
self.conv1 = nn.Conv1d(in_channels, out_channels, kernel_size,
padding=padding, dilation=dilation)
self.conv2 = nn.Conv1d(out_channels, out_channels, kernel_size,
padding=padding, dilation=dilation)
self.net = nn.Sequential(
self.conv1, nn.ReLU(), nn.Dropout(0.2),
self.conv2, nn.ReLU(), nn.Dropout(0.2)
)
# 残差连接
self.downsample = nn.Conv1d(in_channels, out_channels, 1) \
if in_channels != out_channels else None
def forward(self, x):
out = self.net(x)
# 裁剪保持长度
out = out[:, :, :x.size(2)]
res = x if self.downsample is None else self.downsample(x)
return F.relu(out + res)
class TCN(nn.Module):
def __init__(self, input_size, num_channels, kernel_size=2):
super().__init__()
layers = []
num_levels = len(num_channels)
for i in range(num_levels):
dilation = 2 ** i # 指数增长的 dilation
in_ch = input_size if i == 0 else num_channels[i-1]
out_ch = num_channels[i]
layers.append(TCNBlock(in_ch, out_ch, kernel_size, dilation))
self.network = nn.Sequential(*layers)
def forward(self, x):
return self.network(x)
# 使用示例
model = TCN(input_size=10, num_channels=[25, 25, 25, 25])
x = torch.randn(32, 10, 100) # (batch, features, time_steps)
y = model(x)
print(y.shape) # (32, 25, 100)TCN 的优势:
- 超大感受野(通过 dilation)
- 并行计算(不像 RNN 必须串行)
- 梯度稳定(避免 RNN 的梯度消失)
8.3 案例3:语音识别特征提取
python
class SpeechFeatureExtractor(nn.Module):
def __init__(self):
super().__init__()
# 输入:(batch, 1, audio_length) 原始音频波形
# 第1层:提取低级特征
self.conv1 = nn.Conv1d(1, 64, kernel_size=80, stride=4)
self.bn1 = nn.BatchNorm1d(64)
# 第2层:提取中级特征
self.conv2 = nn.Conv1d(64, 128, kernel_size=3, stride=2)
self.bn2 = nn.BatchNorm1d(128)
# 第3层:提取高级特征
self.conv3 = nn.Conv1d(128, 256, kernel_size=3, stride=2)
self.bn3 = nn.BatchNorm1d(256)
def forward(self, x):
# x: (batch, 1, 16000) 假设1秒音频,采样率16kHz
x = F.relu(self.bn1(self.conv1(x)))
# 输出: (batch, 64, 3981)
x = F.relu(self.bn2(self.conv2(x)))
# 输出: (batch, 128, 1990)
x = F.relu(self.bn3(self.conv3(x)))
# 输出: (batch, 256, 994)
return x
# 测试
audio = torch.randn(8, 1, 16000) # 8个1秒音频片段
extractor = SpeechFeatureExtractor()
features = extractor(audio)
print(f"音频特征形状: {features.shape}")设计思路:
- 第一层用大卷积核(80)和大步长(4)快速降维
- 后续层逐步提取抽象特征
- Batch Normalization 稳定训练
9. 批判性思考与扩展
9.1 Conv1d 的局限性
局限1:固定感受野
问题:标准卷积的感受野是固定的,无法灵活适应不同长度的模式。
改进方向:
- Multi-scale Convolution:并行使用不同 kernel_size
- Dilated Convolution:指数增长的 dilation
- Adaptive Convolution:动态调整卷积核
局限2:无法建模长距离依赖
问题:即使堆叠多层,卷积的感受野增长是线性的,难以捕捉超长距离的依赖关系。
解决方案:
- Transformer:全局自注意力机制(但计算量大)
- Conv + Attention:混合架构
- State Space Models (SSM):如 Mamba、S4(新兴方向)
局限3:参数效率问题
问题 :通道数多时,参数量 Cout×Cin×KC_{\text{out}} \times C_{\text{in}} \times KCout×Cin×K 增长快。
解决方案:
- 深度可分离卷积 :参数量降为 Cin×K+Cout×CinC_{\text{in}} \times K + C_{\text{out}} \times C_{\text{in}}Cin×K+Cout×Cin
- 组卷积 :参数量降为 Cout×Cin×KG\frac{C_{\text{out}} \times C_{\text{in}} \times K}{G}GCout×Cin×K
9.2 Conv1d vs. 其他序列建模方法
| 方法 | 优势 | 劣势 | 适用场景 |
|---|---|---|---|
| Conv1d | 并行计算、局部特征强 | 长距离依赖弱 | 音频、信号处理 |
| RNN/LSTM | 天然处理序列 | 串行计算慢、梯度问题 | 语言模型(已过时) |
| Transformer | 全局建模能力强 | 计算量 O(L2)O(L^2)O(L2)、内存大 | NLP、长序列 |
| Mamba/S4 | 线性复杂度、长序列 | 理论复杂、工程不成熟 | 超长序列(新兴) |
9.3 前沿扩展
扩展1:可变形卷积(Deformable Convolution)
python
# 概念示意(实际需要专门库如 torchvision)
class DeformableConv1d(nn.Module):
"""卷积核可以学习偏移量,适应不同的采样位置"""
def __init__(self, in_channels, out_channels, kernel_size):
super().__init__()
self.offset_conv = nn.Conv1d(in_channels, kernel_size, kernel_size)
self.conv = nn.Conv1d(in_channels, out_channels, kernel_size)
def forward(self, x):
offset = self.offset_conv(x) # 学习偏移量
# 根据 offset 调整采样位置(需要特殊实现)
x = self.conv(x)
return x扩展2:注意力增强卷积
python
class ConvWithAttention(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size):
super().__init__()
self.conv = nn.Conv1d(in_channels, out_channels, kernel_size, padding=kernel_size//2)
self.attention = nn.Sequential(
nn.AdaptiveAvgPool1d(1),
nn.Conv1d(out_channels, out_channels//4, 1),
nn.ReLU(),
nn.Conv1d(out_channels//4, out_channels, 1),
nn.Sigmoid()
)
def forward(self, x):
x = self.conv(x)
# 通道注意力:学习每个通道的重要性
attn = self.attention(x) # (batch, channels, 1)
x = x * attn # 加权
return x10. 小结与学习路径建议
10.1 核心收获
通过这份笔记,我们系统掌握了 Conv1d 的:
- 本质认知:卷积 = 对应相乘 + 求和(不是矩阵乘法)
- 维度变化规律 :
- 卷积核形状:(Cout,Cin,K)(C_{\text{out}}, C_{\text{in}}, K)(Cout,Cin,K)
- 输出长度:Lout=Lin+2P−D(K−1)−1S+1L_{\text{out}} = \frac{L_{\text{in}} + 2P - D(K-1) - 1}{S} + 1Lout=SLin+2P−D(K−1)−1+1
- 运算过程:取块 → 对应相乘 → 求和 → 滑动
- 时间与通道纠缠:每个过滤器同时进行时序提取和通道融合
- 工程技巧:组卷积、深度可分离、因果卷积等
10.2 推荐资源
论文:
- ImageNet Classification with Deep Convolutional Neural Networks (AlexNet)
- Very Deep Convolutional Networks for Large-Scale Image Recognition (VGG)
- Deep Residual Learning for Image Recognition (ResNet)
代码库:
- PyTorch 官方教程:
https://pytorch.org/tutorials/ - Papers with Code:
https://paperswithcode.com/
书籍:
- 《Deep Learning》(Goodfellow et al.) - 第9章
- 《Dive into Deep Learning》- 免费在线书
附录:快速参考表
常用 Conv1d 配置
python
# 保持长度不变
nn.Conv1d(in_ch, out_ch, kernel_size=3, padding=1)
# 下采样(长度减半)
nn.Conv1d(in_ch, out_ch, kernel_size=3, stride=2)
# 扩大感受野(空洞卷积)
nn.Conv1d(in_ch, out_ch, kernel_size=3, dilation=2)
# 因果卷积(时间序列预测)
nn.Conv1d(in_ch, out_ch, kernel_size=3, padding=2)[:, :, :-2]
# 深度可分离卷积
nn.Conv1d(ch, ch, kernel_size=3, groups=ch, padding=1) # Depthwise
nn.Conv1d(ch, out_ch, kernel_size=1) # Pointwise调试检查清单
- 输入形状是
(batch, channels, length)吗? -
in_channels与实际输入匹配吗? - 序列长度 ≥ kernel_size 吗?
- 输出长度符合预期吗?(用公式验证)
- 是否需要 padding 保持长度?
- 梯度是否正常反向传播?(检查
requires_grad)