【剑斩OFFER】算法的暴力美学——计算右侧小于当前元素的个数

一、题目原理

二、算法原理

使用归并排序算法（降序）+ 绑定数组下标来解决这道题：

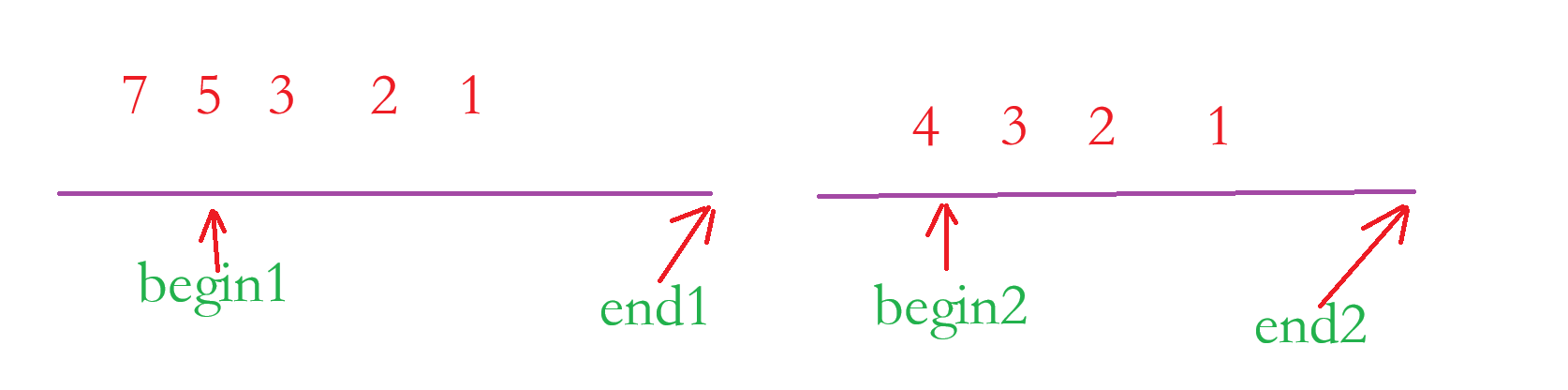
当 nums[ begin1 ] > nums[ begin2 ] 时，end2 - begin2 + 1个数字小于nums[ begin1 ]；例如：7 > 4 ，那么 4 到 1 之间的数字都小于7；

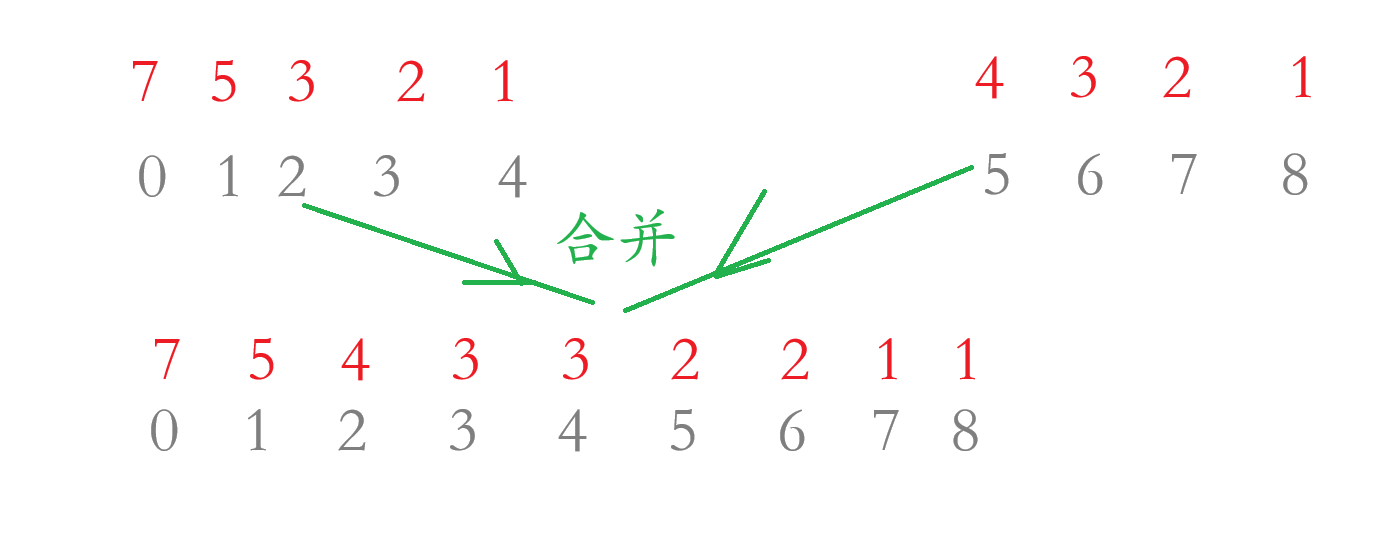
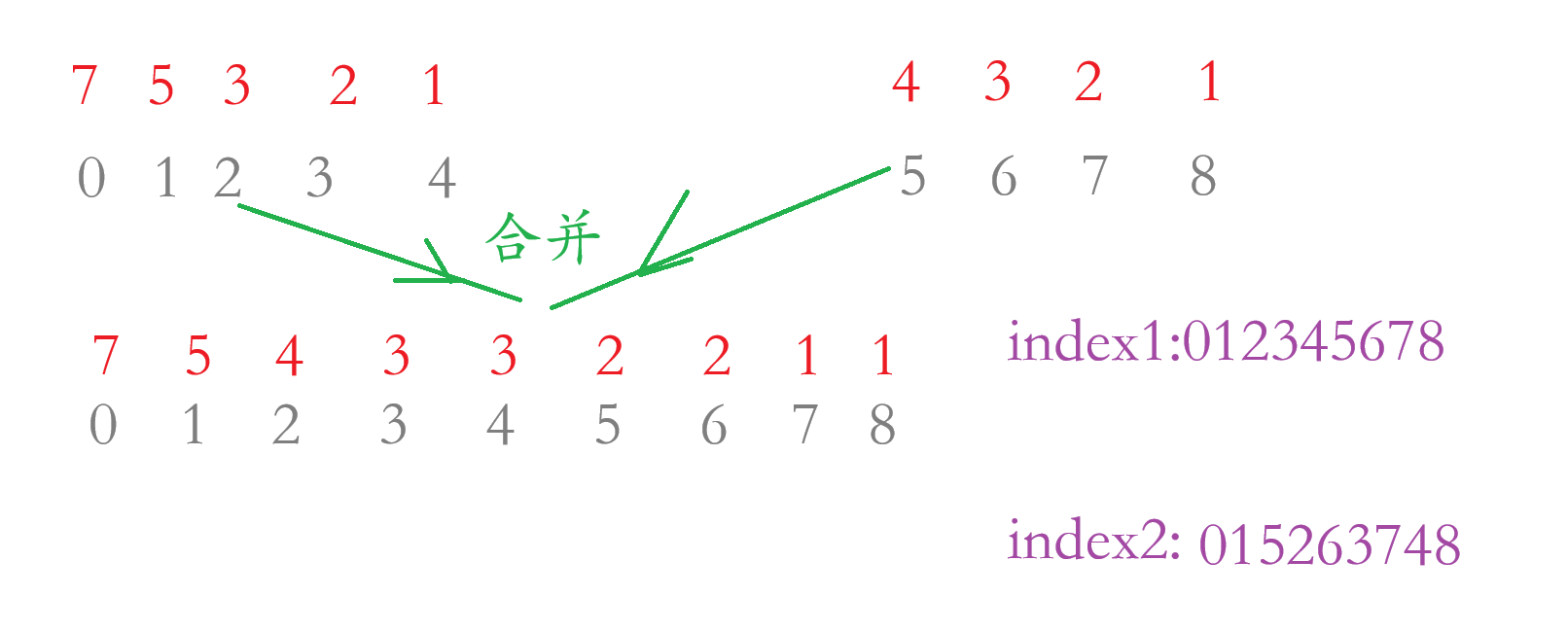
因为在合并两个数组的时候会打乱各个数字的下标，根据题目要求我们是要在原数组的下标来判断每个数字的右边有多少个数字是小于当前数字的，所以我们要弄出两个数组来绑定下标：index1 和 index2 ，其中 index1 是保存原来数组的下标，而 index2 是保存合并数组后各个数字对应原来数组的下标，保证各个数字对应的下标不会乱，到时候再把 index2 里面的数字跟新到 index1 里面：

三、代码实现

cpp 复制代码

class Solution {
    vector<int> tmp;
    vector<int> index1;
    vector<int> index2;
    vector<int> ret;
public:
    vector<int> countSmaller(vector<int>& nums) {
        tmp.resize(nums.size());
        index1.resize(nums.size());
        ret.resize(nums.size());
        index2.resize(nums.size());
        for(int i = 0; i < nums.size();i++) index1[i] = i;
        Quicksort(0,nums.size()-1,nums,tmp);
        return ret;
    }

    void Quicksort(int l,int r,vector<int>& nums,vector<int>& tmp)
    {
        if(l >= r) return;
        
        int keyi = (r + l) >> 1;
        Quicksort(l,keyi,nums,tmp);//左边：【 l , keyi 】
        Quicksort(keyi + 1,r,nums,tmp);//右边：【keyi + 1,r 】

        int begin1 = l,end1 = keyi;//左边数组
        int begin2 = keyi + 1,end2 = r;//右边数组
        int index = l;//遍历起始点



        while(begin1 <= end1 && begin2 <= end2)//比较遍历
        {
            if(nums[begin1] > nums[begin2])
            {
                ret[index1[begin1]] += end2 - begin2 + 1;
                index2[index] = index1[begin1];//绑定下标
                tmp[index++] = nums[begin1++];
            }
            else 
            {
                index2[index] = index1[begin2];
                tmp[index++] = nums[begin2++];
            }
        }

        while(begin1 <= end1)
        {
            index2[index] = index1[begin1];
            tmp[index++] = nums[begin1++];//把左边剩余的数字放到 tmp
        }

        while(begin2 <= end2)
        {
            index2[index] = index1[begin2];
            tmp[index++] = nums[begin2++];//把右边剩余的数字放到 tmp
        }
        
        for(int i = l;i <= r;i++)
        {
            index1[i] = index2[i];
            nums[i] = tmp[i];//把 tmp 里面的数字放回到原数组 nums
        }
    }
};