【C++数据结构进阶】玩转并查集：从原理到实战，C++ 实现与高频面试题全解析

---

目录

前言

[一、并查集是什么？------ 一句话看懂核心本质](#一、并查集是什么？—— 一句话看懂核心本质)

[二、并查集的核心原理 ------ 数组如何模拟 "圈子"？](#二、并查集的核心原理 —— 数组如何模拟 “圈子”？)

[2.1 父指针数组的规则](#2.1 父指针数组的规则)

[初始状态（10 个独立集合）](#初始状态（10 个独立集合）)

一次合并（形成三个小分队）

[第二次合并（西安 + 成都小分队）](#第二次合并（西安 + 成都小分队）)

[2.2 核心操作的原理](#2.2 核心操作的原理)

（1）查找（Find）：找到元素的根节点

（2）合并（Union）：将两个集合合并为一个

（3）统计集合个数（Count）：统计当前不相交集合的数量

[2.3 并查集的优化 ------ 路径压缩（Find 操作的终极优化）](#2.3 并查集的优化 —— 路径压缩（Find 操作的终极优化）)

路径压缩的原理

[三、并查集的 C++ 实现 ------ 完整代码与详细注释](#三、并查集的 C++ 实现 —— 完整代码与详细注释)

[3.1 基础实现（带路径压缩和按大小合并）](#3.1 基础实现（带路径压缩和按大小合并）)

[3.2 代码解释](#3.2 代码解释)

[3.3 递归实现路径压缩（可选）](#3.3 递归实现路径压缩（可选）)

[四、并查集的经典应用场景 ------ 面试高频题实战](#四、并查集的经典应用场景 —— 面试高频题实战)

[4.1 应用一：省份数量（LeetCode 547）](#4.1 应用一：省份数量（LeetCode 547）)

题目描述

示例

解题思路

[C++ 代码实现](#C++ 代码实现)

代码优化点

[4.2 应用二：等式方程的可满足性（LeetCode 990）](#4.2 应用二：等式方程的可满足性（LeetCode 990）)

题目描述

示例

解题思路

[C++ 代码实现](#C++ 代码实现)

关键思路

[4.3 应用三：其他常见场景](#4.3 应用三：其他常见场景)

五、并查集的时间复杂度与空间复杂度分析

[5.1 时间复杂度](#5.1 时间复杂度)

[5.2 空间复杂度](#5.2 空间复杂度)

六、并查集的常见误区与注意事项

[6.1 常见误区](#6.1 常见误区)

[6.2 注意事项](#6.2 注意事项)

总结

---

前言

在编程世界里，有一类问题始终困扰着初学者 ------ 如何高效处理元素的分组、合并与查询？比如判断社交网络中的 "朋友圈" 数量、验证等式方程的可满足性、解决图的连通分量问题等。如果用常规的暴力方法，不仅代码繁琐，效率也会大打折扣。而并查集（Union-Find Set），这个看似简单却极具智慧的数据结构，正是为解决这类问题而生。

它就像一个 "社交圈子管理器"，能轻松实现 "查找某人属于哪个圈子" 和 "将两个圈子合并" 这两个核心操作，且经过优化后，这两个操作的时间复杂度几乎能达到常数级别。本文将从原理入手，带你层层揭开并查集的神秘面纱，让你从 "入门" 到 "精通"，再到 "实战应用"，真正掌握这个面试与工作中的 "利器"。下面就让我们正式开始吧！

---

一、并查集是什么？------ 一句话看懂核心本质

并查集，也叫 disjoint-set（不相交集合），是一种支持快速查找 和合并操作的抽象数据类型，主要用于处理一系列不相交集合的合并与查询问题。

它的核心思想可以用生活中的 "朋友圈" 来理解：

• 初始时，每个人都是一个独立的 "小圈子"（单元素集合）；
• 当两个人成为朋友时，他们所在的 "小圈子" 就会合并成一个 "大圈子"（集合合并）；
• 当我们想知道两个人是否是朋友时，只需判断他们是否在同一个 "圈子" 里（集合查询）。

再举一个更具体的例子：

某公司校招了 10 名新员工，编号 0-9，来自不同城市，起初互不相识（每个员工自成一个集合）。

后来西安的 4 名员工（0、6、7、8）组成小分队，成都的 3 名员工（1、4、9）组成小分队，武汉的 3 名员工（2、3、5）组成小分队（三次集合合并）。

之后，西安的 8 号员工和成都的 1 号员工成为好友，两个小分队又合并成一个大圈子（第四次合并）。我们需要快速回答："3 号和 7 号是否在同一个圈子？""现在总共有多少个圈子？"

------ 这些问题，并用查集都能高效解决。

简单来说，并查集就是管理 "圈子" 的数据结构，核心支持三个操作：查找（Find）、合并（Union）、统计集合个数（Count）。

二、并查集的核心原理 ------ 数组如何模拟 "圈子"？

并查集的实现非常巧妙，通常用一个数组就能模拟所有集合的关系。这个数组我们称之为**"父指针数组"，记为ufs**（Union-Find Set 的缩写），数组的下标对应元素的编号，数组的值则有特殊含义：

2.1 父指针数组的规则

• 若ufs[index] < 0：表示index是一个集合的根节点（"圈子的首领"），其绝对值**|ufs[index]|表示该集合的元素个数**；
• 若ufs[index] >= 0：表示index不是根节点，其值指向该元素的 "父节点"（同一个圈子里的上一级成员）。

我们用之前的员工例子来直观理解：

初始状态（10 个独立集合）

每个员工都是自己的 "首领"，集合大小为 1，所以数组所有元素都为 - 1：

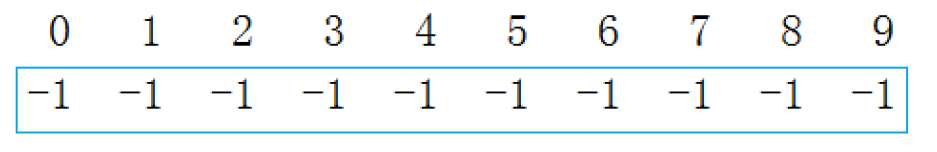
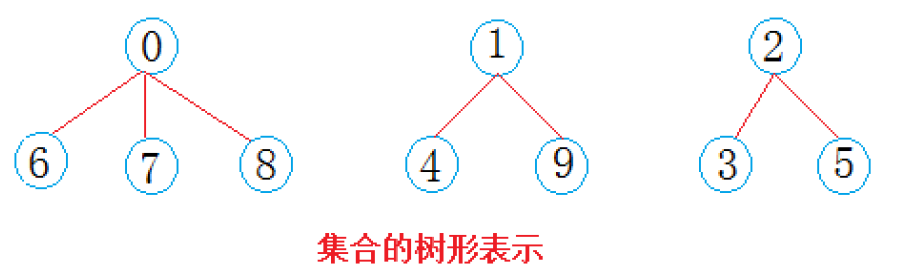
一次合并（形成三个小分队）

• 西安小分队（0、6、7、8）：以 0 为根，6、7、8 的父节点都是 0，集合大小为 4，所以ufs[0] = -4，ufs[6] = 0，ufs[7] = 0，ufs[8] = 0；
• 成都小分队（1、4、9）：以 1 为根，4、9 的父节点都是 1，集合大小为 3，所以ufs[1] = -3，ufs[4] = 1，ufs[9] = 1；
• 武汉小分队（2、3、5）：以 2 为根，3、5 的父节点都是 2，集合大小为 3，所以ufs[2] = -3，ufs[3] = 2，ufs[5] = 2。

此时数组状态：

索引：0 1 2 3 4 5 6 7 8 9
ufs：-4 -3 -3 2 1 2 0 0 0 1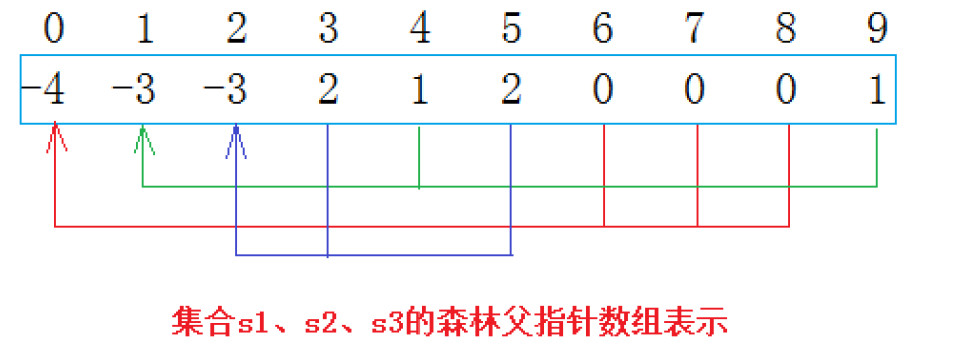

第二次合并（西安 + 成都小分队）

8 号（属于 0 的集合）和 1 号（属于 1 的集合）合并，将两个集合合并为一个。此时 0 成为新的根，集合大小为 4+3=7，所以ufs[0] = -7，ufs[1] = 0（1 的父节点变为 0）。

最终数组状态：

索引：0 1 2 3 4 5 6 7 8 9
ufs：-7 0 -3 2 1 2 0 0 0 1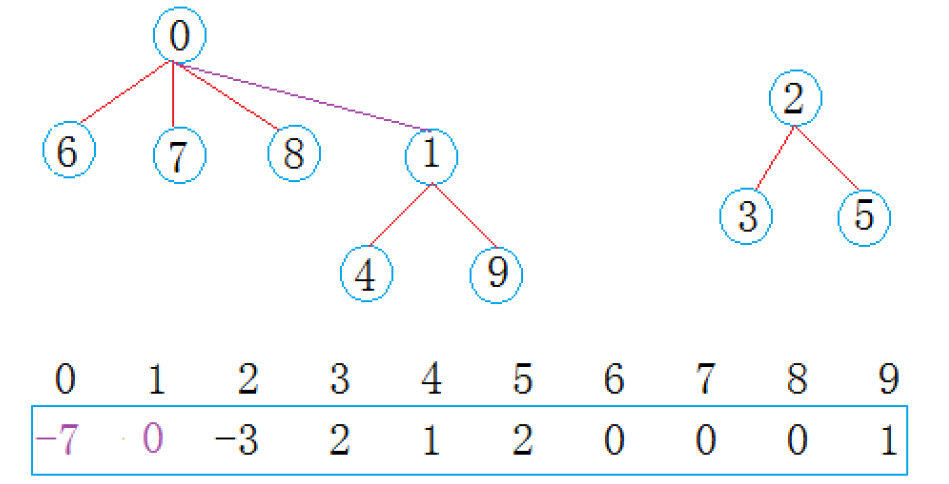

通过这个数组，我们能快速获取以下信息：

• 查找元素 6 的根 ：ufs[6] = 0（非负），继续查ufs[0] = -7（负），所以根是 0，属于大小为 7 的集合；
• 判断元素 3 和 7 是否同属一个集合：3 的根是 2，7 的根是 0，根不同，所以不属于同一个集合；
• 统计集合个数：数组中负数的个数（0 和 2 对应的 - 7、-3），共 2 个集合。

2.2 核心操作的原理

并查集的核心是三个操作：查找（Find）、合并（Union）、统计集合个数（Count），其原理如下：

（1）查找（Find）：找到元素的根节点

查找操作的目标是，给定一个元素编号，沿着父指针一直向上追溯，直到找到根节点（数组值为负数的元素）。

步骤：

1. 若当前元素的**ufs值为负数**，直接返回该元素（根节点）；
2. 若为非负数，将当前元素更新为其父节点，重复步骤 1，直到找到根节点。

例如，查找元素 9 的根：

• ufs[9] = 1（非负）→ 父节点是 1；
• ufs[1] = 0（非负）→ 父节点是 0；
• ufs[0] = -7（负）→ 根节点是 0，返回 0。

（2）合并（Union）：将两个集合合并为一个

合并操作的目标是，将两个不同集合的根节点连接起来，形成一个新的集合。

步骤：

1. 分别找到两个元素的根节点root1和root2；
2. 若root1 == root2：两个元素已在同一个集合，合并失败，返回false；
3. 若root1 != root2：将较小的集合合并到较大的集合（优化策略，避免树过深），更新根节点的集合大小（ufs[root1] += ufs[root2]），并将较小集合的根节点的父指针指向较大集合的根节点（ufs[root2] = root1），合并成功，返回true。

为什么要 "小集合合并到大连合"？这是为了避免树的高度过高，导致后续查找操作变慢。比如，如果总是把大连合合并到小集合，可能会形成一条长长的链（如 1→2→3→...→n），查找根节点需要 O (n) 时间；而 "小合并到大" 能保证树的高度始终较低，查找效率更高。

（3）统计集合个数（Count）：统计当前不相交集合的数量

由于根节点的**ufs**值为负数，非根节点为非负数，所以只需遍历整个数组，统计负数的个数即可。

例如，初始状态数组有 10 个负数，集合个数为 10；合并为三个小分队后，数组有 3 个负数，集合个数为 3；合并西安和成都小分队后，数组有 2 个负数，集合个数为 2。

2.3 并查集的优化 ------ 路径压缩（Find 操作的终极优化）

在上述基础实现中，查找操作的效率取决于树的高度。如果树的高度过高（如链式结构），查找操作的时间复杂度会退化到 O (n)。为了进一步优化查找效率，我们可以引入**"路径压缩"**技术。

路径压缩的原理

路径压缩是指，在执行查找操作时，将查找路径上的所有元素的父指针直接指向根节点。这样一来，下次再查找这些元素时，就能直接找到根节点，大大减少查找次数。

举个例子：原来的查找路径是 9→1→0（根节点），执行路径压缩后，9 的父指针直接指向 0，下次查找 9 时，一步就能找到根节点。

路径压缩的实现非常简单，只需在 Find操作中，将当前元素的父节点更新为根节点 即可（可以用递归或迭代实现）。优化后的Find操作，时间复杂度几乎能达到 O (1)（均摊时间复杂度）。

三、并查集的 C++ 实现 ------ 完整代码与详细注释

基于上述原理，我们用 C++ 实现一个通用的并查集类，包含查找（带路径压缩）、合并（小集合合并到大集合）、统计集合个数三个核心操作。

3.1 基础实现（带路径压缩和按大小合并）

#include <vector>
#include <iostream>
using namespace std;

// 并查集类
class UnionFindSet {
public:
    // 构造函数：初始化并查集，每个元素自成一个集合（值为-1）
    UnionFindSet(size_t size) : _ufs(size, -1) {}

    // 查找操作：找到元素index的根节点，带路径压缩
    int FindRoot(int index) {
        // 边界检查：index必须在合法范围内
        if (index < 0 || index >= _ufs.size()) {
            throw invalid_argument("index out of range");
        }
        // 迭代实现路径压缩：找到根节点后，回溯更新路径上所有元素的父节点
        int root = index;
        // 第一步：找到根节点
        while (_ufs[root] >= 0) {
            root = _ufs[root];
        }
        // 第二步：路径压缩，将index到root路径上的所有元素直接指向root
        while (_ufs[index] >= 0) {
            int parent = _ufs[index]; // 保存当前元素的父节点
            _ufs[index] = root;       // 将当前元素的父节点更新为根节点
            index = parent;           // 继续处理下一个元素
        }
        return root;
    }

    // 合并操作：将x1和x2所在的集合合并，返回是否合并成功
    bool Union(int x1, int x2) {
        // 找到两个元素的根节点
        int root1 = FindRoot(x1);
        int root2 = FindRoot(x2);

        // 如果根节点相同，说明已经在同一个集合，无需合并
        if (root1 == root2) {
            return false;
        }

        // 按大小合并：将较小的集合合并到较大的集合
        // _ufs[root]为负数，绝对值是集合大小，所以比较时用">"（因为-3 > -4，代表大小3 < 4）
        if (_ufs[root1] > _ufs[root2]) { // root1的集合更小
            swap(root1, root2); // 保证root1是较大集合的根
        }

        // 合并：更新较大集合的大小，将较小集合的根指向较大集合的根
        _ufs[root1] += _ufs[root2]; // 集合大小相加（负数相加）
        _ufs[root2] = root1;        // 小集合的根指向大集合的根

        return true;
    }

    // 统计集合个数：数组中负数的个数
    size_t Count() const {
        size_t count = 0;
        for (int e : _ufs) {
            if (e < 0) {
                ++count;
            }
        }
        return count;
    }

    // 辅助函数：打印并查集数组（用于调试）
    void PrintUFS() const {
        cout << "并查集数组状态：";
        for (int e : _ufs) {
            cout << e << " ";
        }
        cout << endl;
    }

private:
    vector<int> _ufs; // 父指针数组，存储集合关系
};

// 测试代码
int main() {
    // 初始化10个元素（编号0-9）
    UnionFindSet ufs(10);
    cout << "初始状态：" << endl;
    ufs.PrintUFS();
    cout << "当前集合个数：" << ufs.Count() << endl; // 输出10

    // 合并西安小分队（0、6、7、8）
    ufs.Union(0, 6);
    ufs.Union(0, 7);
    ufs.Union(0, 8);
    cout << "\n合并西安小分队后：" << endl;
    ufs.PrintUFS();
    cout << "当前集合个数：" << ufs.Count() << endl; // 输出8（10-3=7？不对，初始10，合并3次，减少3个集合，10-3=7）

    // 合并成都小分队（1、4、9）
    ufs.Union(1, 4);
    ufs.Union(1, 9);
    cout << "\n合并成都小分队后：" << endl;
    ufs.PrintUFS();
    cout << "当前集合个数：" << ufs.Count() << endl; // 输出6（7-2=5？哦，初始10，合并0&6（9）、0&7（8）、0&8（7）；合并1&4（6）、1&9（5），所以是5）

    // 合并武汉小分队（2、3、5）
    ufs.Union(2, 3);
    ufs.Union(2, 5);
    cout << "\n合并武汉小分队后：" << endl;
    ufs.PrintUFS();
    cout << "当前集合个数：" << ufs.Count() << endl; // 输出3（5-2=3）

    // 合并西安和成都小分队（8和1）
    ufs.Union(8, 1);
    cout << "\n合并西安和成都小分队后：" << endl;
    ufs.PrintUFS();
    cout << "当前集合个数：" << ufs.Count() << endl; // 输出2（3-1=2）

    // 查找元素9的根节点
    int root9 = ufs.FindRoot(9);
    cout << "\n元素9的根节点：" << root9 << endl; // 输出0

    // 判断元素3和7是否同属一个集合
    int root3 = ufs.FindRoot(3);
    int root7 = ufs.FindRoot(7);
    cout << "元素3的根节点：" << root3 << endl; // 输出2
    cout << "元素7的根节点：" << root7 << endl; // 输出0
    cout << "元素3和7是否同属一个集合：" << (root3 == root7 ? "是" : "否") << endl; // 输出否

    return 0;
}

3.2 代码解释

• 构造函数 ：接收集合大小size，初始化_ufs数组为size个 - 1，每个元素自成一个集合；
• FindRoot 函数：迭代实现路径压缩，分两步：①找到根节点；②将路径上所有元素的父指针指向根节点，确保下次查找更快；
• Union 函数：按集合大小合并，将较小集合合并到较大集合，避免树过深，提高查找效率；
• Count 函数：遍历数组统计负数个数，即集合个数；
• PrintUFS 函数：辅助调试，打印当前并查集数组状态。

3.3 递归实现路径压缩（可选）

除了迭代实现，FindRoot也可以用递归实现路径压缩，代码更简洁：

// 递归实现查找（带路径压缩）
int FindRootRecursive(int index) {
    if (index < 0 || index >= _ufs.size()) {
        throw invalid_argument("index out of range");
    }
    // 递归终止条件：找到根节点（_ufs[index] < 0）
    if (_ufs[index] < 0) {
        return index;
    }
    // 路径压缩：将当前元素的父节点更新为根节点，递归查找
    _ufs[index] = FindRootRecursive(_ufs[index]);
    return _ufs[index];
}

递归实现的优点是代码简洁，但缺点是当集合元素较多、树较深时，可能会导致栈溢出（递归深度超过系统栈限制）。因此，实际开发中更推荐使用迭代实现。

四、并查集的经典应用场景 ------ 面试高频题实战

并查集的应用非常广泛，尤其在图论、动态连通性问题中。下面我们结合两道 LeetCode 高频面试题，讲解并查集的实际应用。

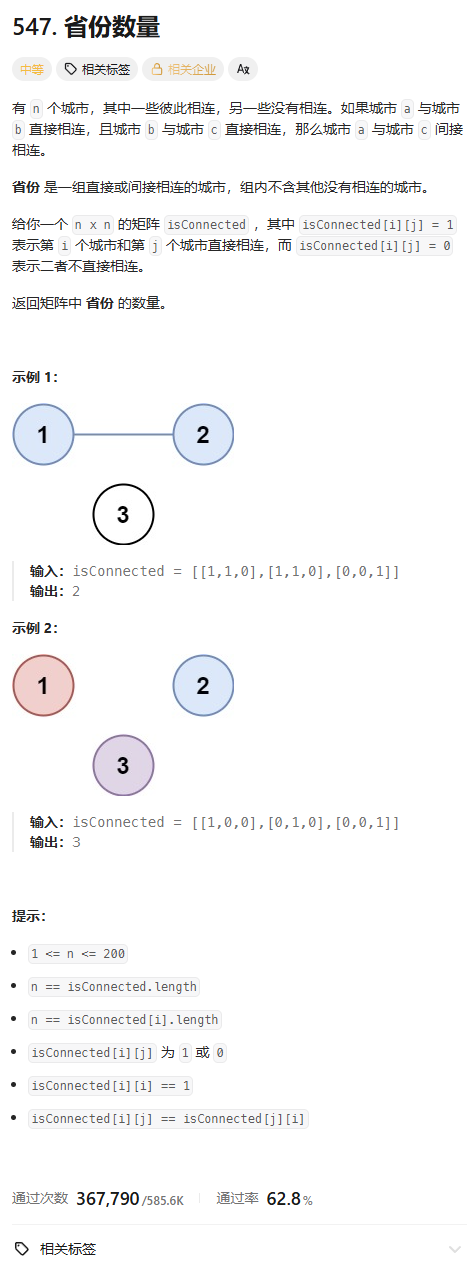
4.1 应用一：省份数量（LeetCode 547）

题目链接：https://leetcode.cn/problems/number-of-provinces/description/

题目描述

有n个城市，其中一些彼此相连，另一些没有相连。如果城市a与城市b直接相连，且城市b与城市c直接相连，那么城市a与城市c间接相连。一个 "省份" 是由一组直接或间接相连的城市组成，组内不含其他没有相连的城市。给你一个n x n的矩阵isConnected，其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连，isConnected[i][j] = 0表示不直接相连。返回矩阵中省份的数量。

示例

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]

输出：2

解释：有 2 个省份，[0,1] 和 [2]。

解题思路

这道题本质上是求图的连通分量个数，用并查集可以轻松解决：

1. 初始化并查集，每个城市自成一个集合；
2. 遍历矩阵isConnected，如果isConnected[i][j] = 1（i 和 j 直接相连），则合并i和j所在的集合；
3. 最终并查集中的集合个数，就是省份的数量。

C++ 代码实现

#include <vector>
using namespace std;

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        if (n == 0) {
            return 0;
        }
        // 初始化并查集，n个城市，每个城市初始为-1
        vector<int> ufs(n, -1);

        // 查找函数（带路径压缩，lambda表达式）
        auto findRoot = [&ufs](int x) {
            int root = x;
            // 找到根节点
            while (ufs[root] >= 0) {
                root = ufs[root];
            }
            // 路径压缩
            while (ufs[x] >= 0) {
                int parent = ufs[x];
                ufs[x] = root;
                x = parent;
            }
            return root;
        };

        // 遍历矩阵，合并相连的城市
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) { // j从i+1开始，避免重复合并（i和j与j和i是一样的）
                if (isConnected[i][j] == 1) {
                    int root1 = findRoot(i);
                    int root2 = findRoot(j);
                    if (root1 != root2) {
                        // 按大小合并
                        if (ufs[root1] > ufs[root2]) {
                            swap(root1, root2);
                        }
                        ufs[root1] += ufs[root2];
                        ufs[root2] = root1;
                    }
                }
            }
        }

        // 统计集合个数（省份数量）
        int count = 0;
        for (int e : ufs) {
            if (e < 0) {
                ++count;
            }
        }
        return count;
    }
};

// 测试代码
int main() {
    vector<vector<int>> isConnected1 = {{1,1,0},{1,1,0},{0,0,1}};
    Solution sol;
    cout << "省份数量：" << sol.findCircleNum(isConnected1) << endl; // 输出2

    vector<vector<int>> isConnected2 = {{1,0,0},{0,1,0},{0,0,1}};
    cout << "省份数量：" << sol.findCircleNum(isConnected2) << endl; // 输出3

    return 0;
}

代码优化点

• 遍历矩阵时，j从i+1开始，避免重复处理(i,j)和(j,i)，减少合并次数；
• 查找函数使用迭代实现路径压缩，避免栈溢出；
• 合并时按集合大小合并，优化树的高度。

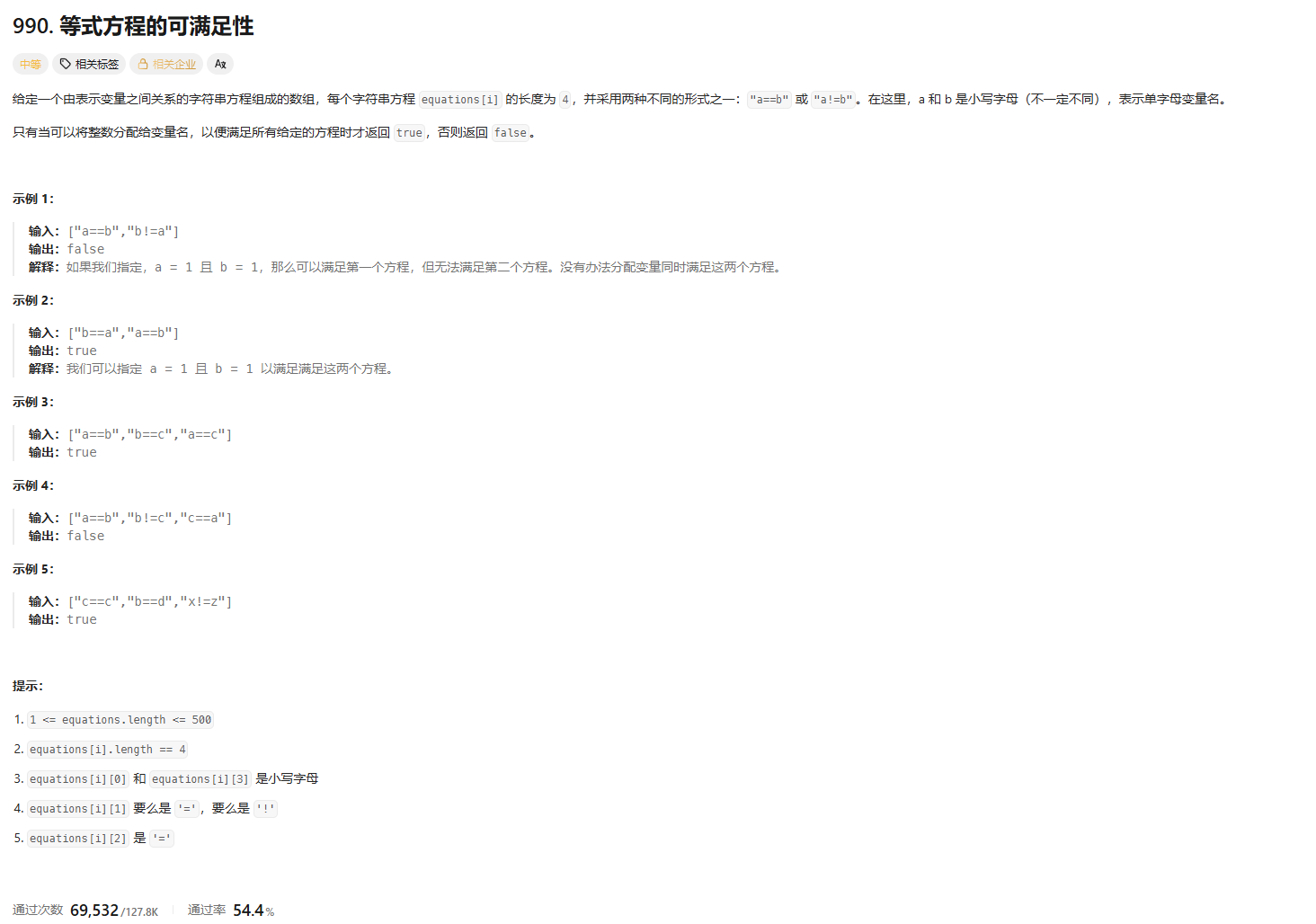
4.2 应用二：等式方程的可满足性（LeetCode 990）

题目链接：https://leetcode.cn/problems/satisfiability-of-equality-equations/description/

题目描述

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程equations[i]的长度为 4，并采用两种形式之一："a==b"或"a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。只有当可以为变量分配整数的值，使得所有给定的方程都满足时，才返回true，否则返回false。

示例

输入1：["a==b","b!=a"]

输出1：false

解释1："a==b"和"b!=a"矛盾，无法同时满足。

输入2：["a==b","b==c","a==c"]

输出2：true

解释2：所有方程都满足。

解题思路

这道题的核心是 "相等关系具有传递性"，可以用并查集来处理：

1. 首先处理所有 "==" 方程：将相等的变量合并到同一个集合中（因为相等关系传递，a==b 且 b==c，则 a、b、c 在同一个集合）；
2. 然后处理所有 "!=" 方程 ：检查两个变量是否在同一个集合中。如果在，则矛盾，返回false；如果不在，则满足条件；
3. 所有方程处理完毕后，返回true。

C++ 代码实现

#include <vector>
#include <string>
using namespace std;

class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        // 26个小写字母，初始化并查集
        vector<int> ufs(26, -1);

        // 查找函数（带路径压缩）
        auto findRoot = [&ufs](int x) {
            int root = x;
            while (ufs[root] >= 0) {
                root = ufs[root];
            }
            // 路径压缩
            while (ufs[x] >= 0) {
                int parent = ufs[x];
                ufs[x] = root;
                x = parent;
            }
            return root;
        };

        // 第一步：处理所有"=="方程，合并相等的变量
        for (const string& eq : equations) {
            if (eq[1] == '=') { // 是"=="方程
                char c1 = eq[0];
                char c2 = eq[3];
                int x = c1 - 'a'; // 转换为0-25的索引
                int y = c2 - 'a';
                int root1 = findRoot(x);
                int root2 = findRoot(y);
                if (root1 != root2) {
                    // 按大小合并
                    if (ufs[root1] > ufs[root2]) {
                        swap(root1, root2);
                    }
                    ufs[root1] += ufs[root2];
                    ufs[root2] = root1;
                }
            }
        }

        // 第二步：处理所有"!="方程，检查是否矛盾
        for (const string& eq : equations) {
            if (eq[1] == '!') { // 是"!="方程
                char c1 = eq[0];
                char c2 = eq[3];
                int x = c1 - 'a';
                int y = c2 - 'a';
                int root1 = findRoot(x);
                int root2 = findRoot(y);
                if (root1 == root2) { // 两个变量在同一个集合，矛盾
                    return false;
                }
            }
        }

        // 所有方程都满足
        return true;
    }
};

// 测试代码
int main() {
    vector<string> equations1 = {"a==b","b!=a"};
    Solution sol;
    cout << (sol.equationsPossible(equations1) ? "true" : "false") << endl; // 输出false

    vector<string> equations2 = {"a==b","b==c","a==c"};
    cout << (sol.equationsPossible(equations2) ? "true" : "false") << endl; // 输出true

    vector<string> equations3 = {"a==b","b!=c","c==a"};
    cout << (sol.equationsPossible(equations3) ? "true" : "false") << endl; // 输出false

    return 0;
}

关键思路

• 相等关系是传递的，适合用并查集合并；
• 不等关系是直接的，只需检查两个变量是否在同一个集合即可；
• 必须先处理所有 "==" 方程，再处理 "!=" 方程，否则会出现逻辑错误（比如先处理 "a!=b"，再处理 "a==b"，此时无法发现矛盾）。

4.3 应用三：其他常见场景

除了上述两道题，并查集还有很多经典应用：

1. 最小生成树（Kruskal 算法）：用并查集判断边的两个顶点是否在同一个集合，避免生成环；
2. 岛屿数量（LeetCode 200）：可以用并查集合并相邻的陆地，最终统计集合个数；
3. 冗余连接（LeetCode 684）：找到导致图中有环的边，用并查集判断边的两个顶点是否已连通；
4. 朋友圈问题：与省份数量类似，统计社交网络中的连通分量个数。

这些问题的核心思想都是**"动态连通性"**，并查集是解决这类问题的最优选择。

五、并查集的时间复杂度与空间复杂度分析

5.1 时间复杂度

并查集的时间复杂度主要取决于查找（Find） 和**合并（Union）**操作，经过路径压缩和按大小 / 秩合并优化后：

• 查找操作的均摊时间复杂度为 O (α(n))，其中 α 是阿克曼函数的反函数；
• 合并操作的时间复杂度由查找操作决定，也是 O (α(n))；
• 统计集合个数的时间复杂度为 O (n)，其中 n 是元素个数。

阿克曼函数 α(n) 增长极其缓慢，在实际应用中，α(n) 几乎可以看作是一个常数（对于 n < 10^60，α(n) ≤ 6）。因此，优化后的并查集可以看作是 "近常数时间" 的数据结构，效率极高。

5.2 空间复杂度

并查集的空间复杂度为 O (n)，其中 n 是元素个数，因为需要一个大小为 n 的数组存储父指针信息。

六、并查集的常见误区与注意事项

6.1 常见误区

1. 忘记边界检查：查找或合并时，元素索引可能超出数组范围，导致数组越界；
2. 路径压缩实现错误：递归实现时未考虑栈溢出，迭代实现时未正确更新父指针；
3. 合并时未按大小 / 秩合并：导致树的高度过高，查找效率退化；
4. 处理顺序错误：如等式方程问题中，先处理 "!=" 再处理 "=="，导致无法发现矛盾；
5. 根节点判断错误：误将非负数当作根节点，或负数当作非根节点。

6.2 注意事项

1. 始终确保元素索引在合法范围内，必要时添加边界检查；
2. 优先使用迭代实现路径压缩，避免栈溢出；
3. 合并时务必按大小或秩合并，优化树的高度；
4. 根据问题逻辑，确定正确的处理顺序（如先合并后查询）；
5. 牢记父指针数组的规则：负数是根节点，绝对值是集合大小；非负数是父节点索引。

---

总结

并查集是一种简单而强大的数据结构，核心解决 "动态连通性" 问题，通过路径压缩和按大小 / 秩合并优化后，效率几乎达到常数级别。它的代码实现简洁，应用场景广泛，是面试中高频考察的知识点。

并查集的魅力在于其简洁的思想和高效的实现，掌握它不仅能帮助你轻松应对面试题，还能让你在处理实际问题时多一种高效的解决方案。希望本文能带你真正理解并查集，让这个强大的数据结构成为你的 "编程利器"！

如果觉得本文对你有帮助，欢迎点赞、收藏、转发，也欢迎在评论区交流讨论～