目录
[二**、ruby和薯条(排序 + 二分 /滑动窗口+前缀和 )](#二**、ruby和薯条(排序 + 二分 /滑动窗口+前缀和 ))
九*、买卖股票的最佳时机IV(多状态dp,"k次交易"注意初始化)
一、kotori和抽卡(二)(组合数Cmn)
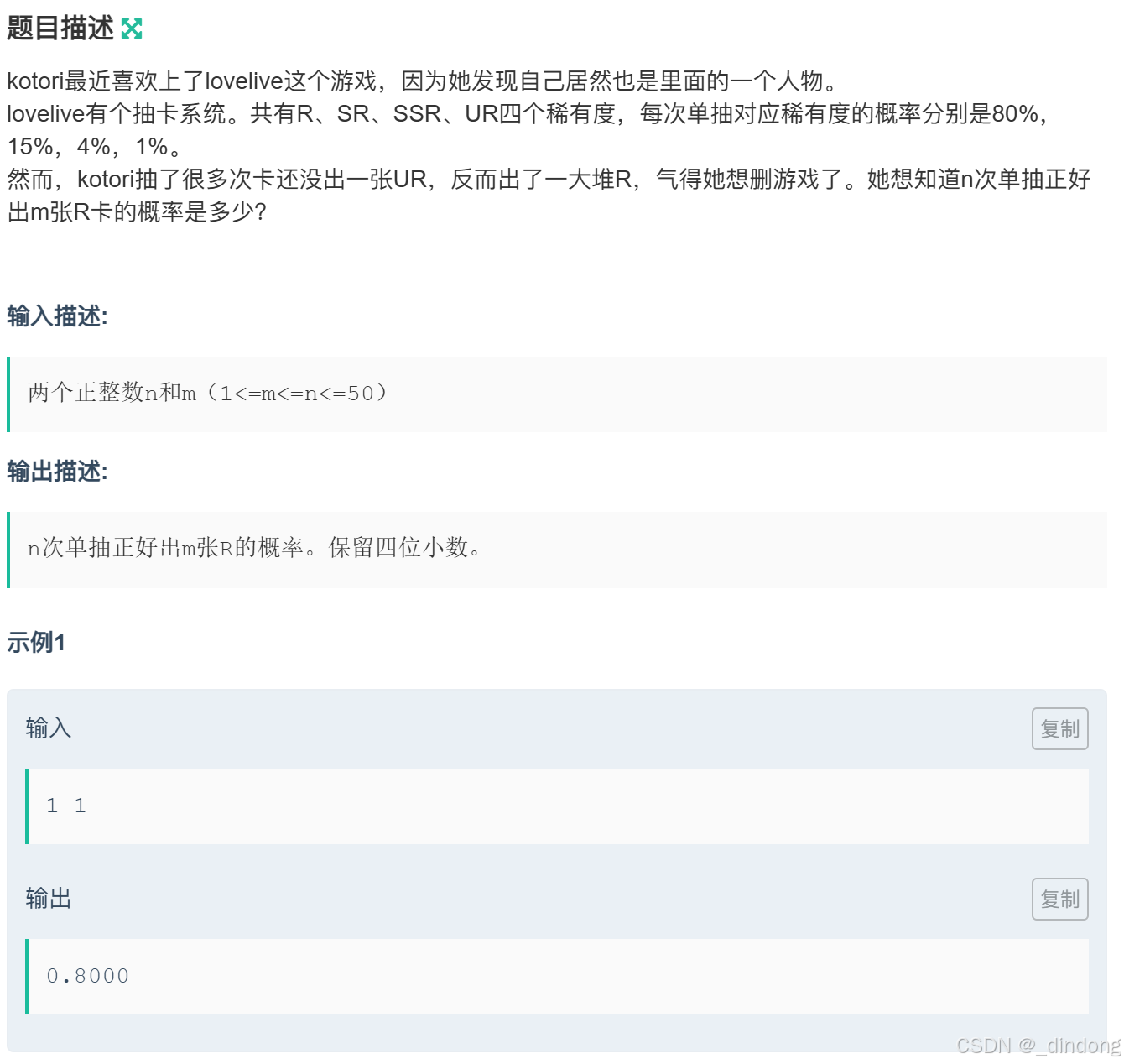
今天刚做组合数的模板题,思路被干扰了,这里数据量这么小还是返璞归真
cpp
#include<iostream>
#include<cmath>
using namespace std;
//3次出两张 c32*p^2*(1-p)^1
int n,m;
int main(){
cin>>n>>m;
double ret=1.0;
for(int i=n;i>n-m;--i) ret*=i;
for(int i=m;i>=2;--i) ret/=i;
printf("%.4f",ret*pow(0.8,m)*pow(0.2,n-m));
}二**、ruby和薯条(排序 + 二分 /滑动窗口+前缀和 )


首先很自然的能想到能对数组排序,然后去找配对
这里配对需要暴力找吗?比如固定一个数,然后去前边暴力查找区间?注意到数组已经排序了,针对排序数组最好的查找算法不就是二分,做题一定要想到这点。
cpp
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int n,l,r;
const int N=2e5+10;
int arr[N];
//排序+二分
int main(){
cin>>n>>l>>r;
for(int i=0;i<n;++i) cin>>arr[i];
sort(arr,arr+n);
LL ret=0;
for(int i=1;i<n;++i){//从第二个数开始枚举 1 2 3 5 6
int left=0,right=i-1;
int L,R;//记录左端点和右端点
while(left<right){
int mid=left+(right-left)/2;
if(arr[mid]<arr[i]-r) left=mid+1;
else right=mid;
}
//这种情况就是可能找到的数字也是不满足的
if(arr[left]>=arr[i]-r) L=left;
else L=left+1;
left=0,right=i-1;//找右端点
while(left<right){
int mid=left+(right-left+1)/2;
if(arr[mid]<=arr[i]-l) left=mid;
else right=mid-1;
}
//这种情况就是可能找到的数字也是不满足的
if(arr[left]<=arr[i]-l) R=left;
else R=left-1;
if(R>=L) ret+=R-L+1;
}
cout<<ret;
return 0;
}解法二就是模拟前几天刷的滑动窗口那题,用前缀和的思想f[l]-f[r-1],感觉有点偏暴力了
cpp
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int n,l,r;
const int N=2e5+10;
int arr[N];
LL find(int x){
LL ret=0;
for(int left=0,right=0;right<n;++right){
while(arr[right]-arr[left]>x) ++left;
ret+=right-left;
}
return ret;
}
int main(){
cin>>n>>l>>r;
for(int i=0;i<n;++i) cin>>arr[i];
sort(arr,arr+n);
cout<<find(r)-find(l-1)<<endl;
}三**、循环汉诺塔(递推)
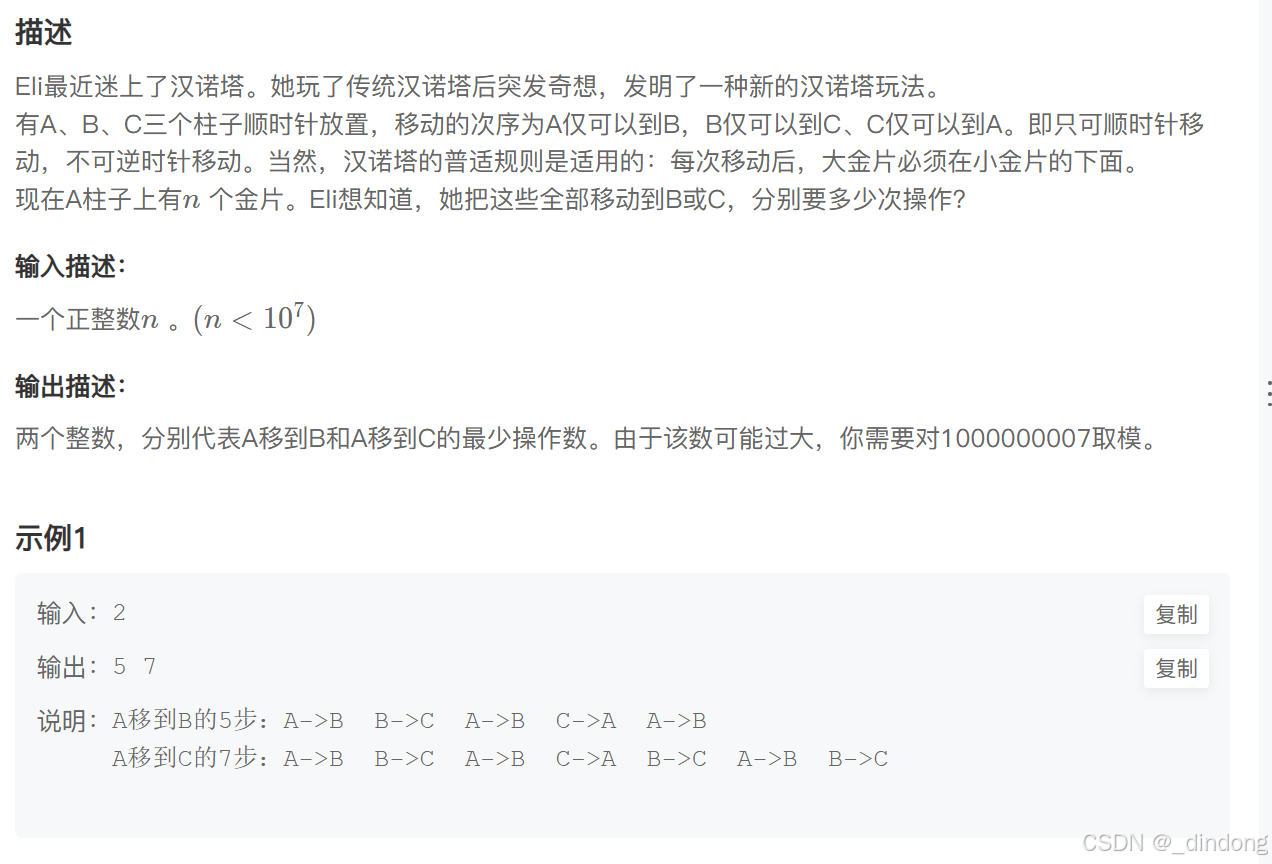
毫无思路的一题
遇到这种情况,还是先举几个小的自己模拟
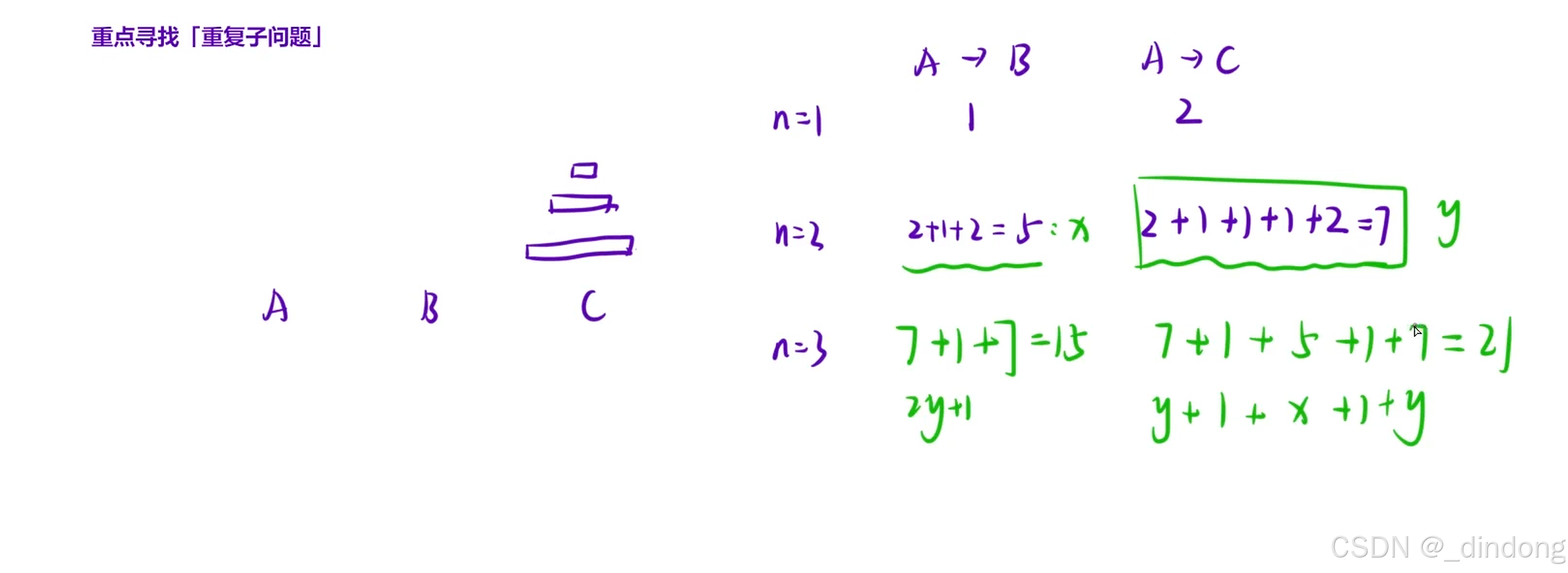
cpp
#include <iostream>
using namespace std;
const int MOD=1e9+7;
int main() {
int n;cin>>n;
int x=1,y=2;
for(int i=2;i<=n;++i)
{
int tmpx=x,tmpy=y;
x=(2*tmpy+1)%MOD;
y=(2*tmpy%MOD+tmpx+2)%MOD;
}
cout<<x<<" "<<y;
return 0;
}四、最小差值(排序)
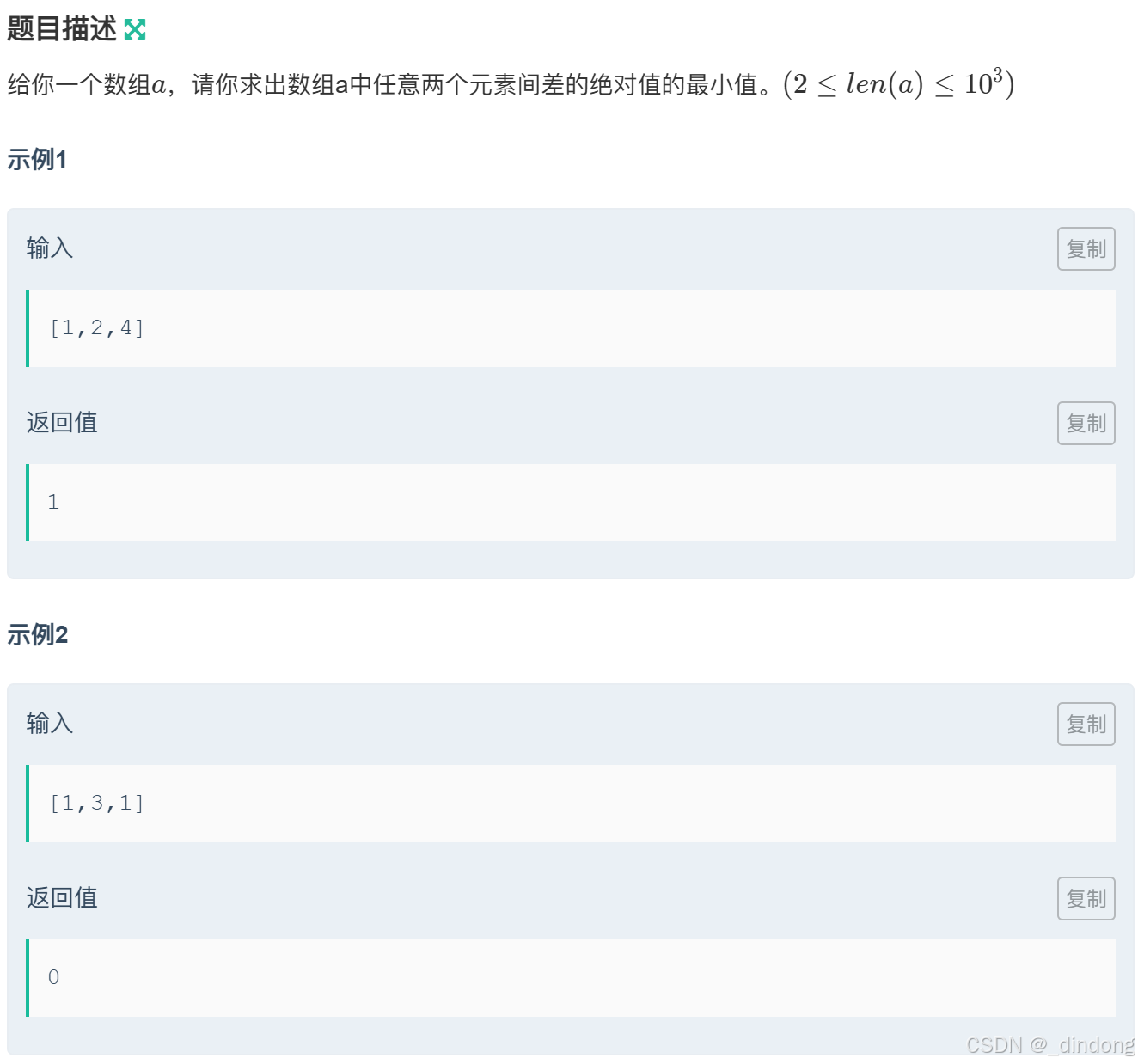
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,arr[N];
int main() {
cin>>n;
for(int i=0;i<n;++i)cin>>arr[i];
sort(arr,arr+n);
int gap=0x3f3f3f3f;
for(int i=0;i<n-1;++i)
{
if(arr[i+1]-arr[i]<gap) gap=arr[i+1]-arr[i];
}
cout<<gap;
return 0;
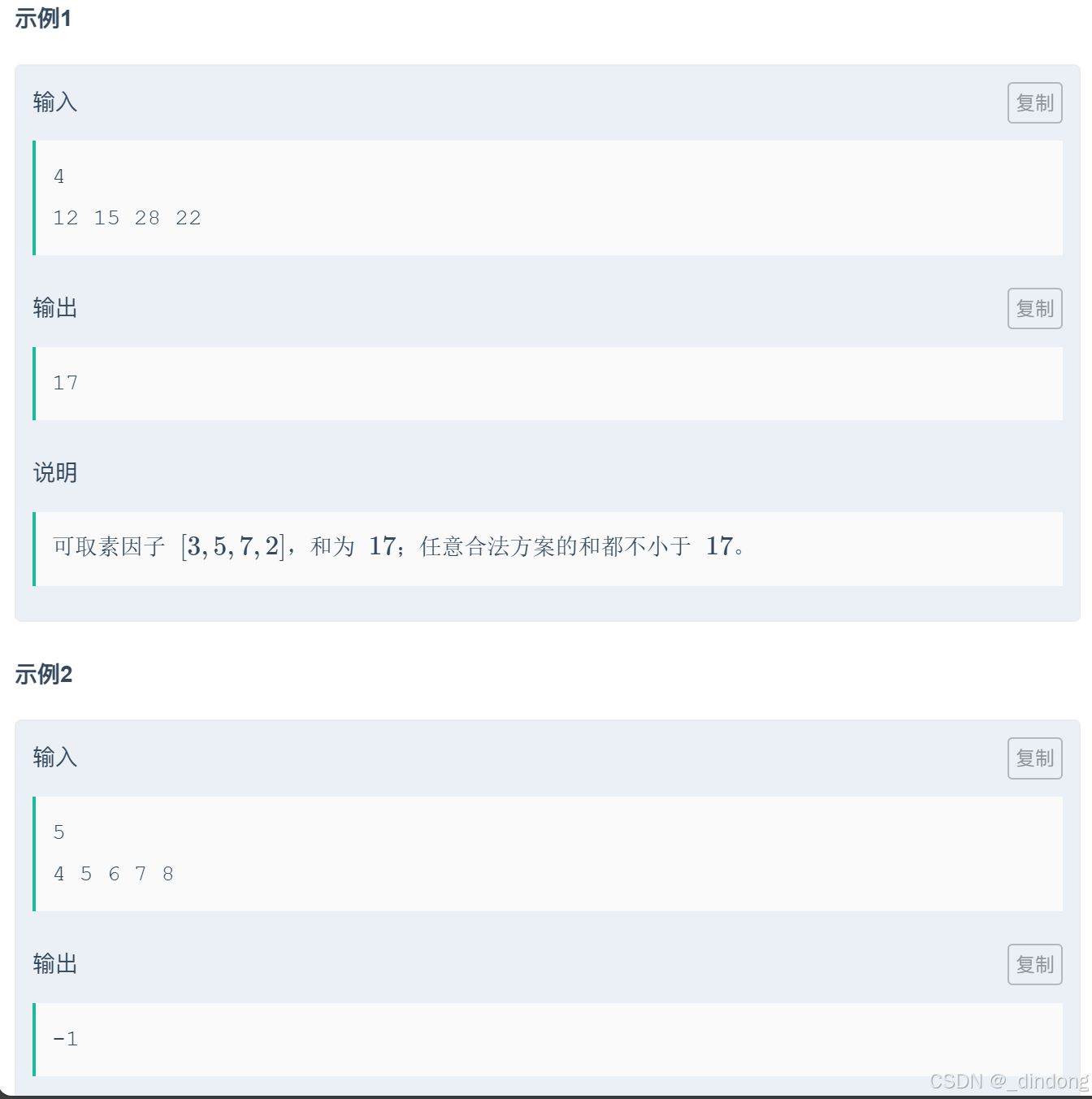
}五**、kotori和素因子(枚举+dfs)
居然是直接dfs,我服了,果然想不出最优算法的时候就要退其次,先看暴力

cpp
#include<bits/stdc++.h>
using namespace std;
int n,sum=INT_MAX;
bool check[1000];
void dfs(vector<vector<int>>& prime,int pos,int path)
{
if (pos==n)
{
sum=min(sum,path);
return;
}
int sz=prime[pos].size();
for (int i=0;i<sz;i++)
{
if (!check[prime[pos][i]])
{
check[prime[pos][i]]=true;
dfs(prime,pos+1,path+prime[pos][i]);
check[prime[pos][i]]=false;
}
}
}
int main()
{
cin>>n;
vector<vector<int>> prime(n);
//存储质因子个数
unordered_map<int,int> PrimeCount;
int cnt=0,num;
while (cnt<n)
{
cin>>num;
if (num%2==0)
{
prime[cnt].push_back(2);
++PrimeCount[2];
while (num%2==0)num/=2;
}
for (int i=3;i*i<=num;i+=2)
{
if (num%i==0)
{
prime[cnt].push_back(i);
++PrimeCount[i];
while (num%i==0)num/=i;
}
}
if (num>1)
{
prime[cnt].push_back(num);
++PrimeCount[num];
}
++cnt;
}
//dfs
if (PrimeCount.size()<n)sum=-1;
else dfs(prime,0,0);
cout<<sum;
return 0;
}六**、dd爱科学1.0(贪心+二分)
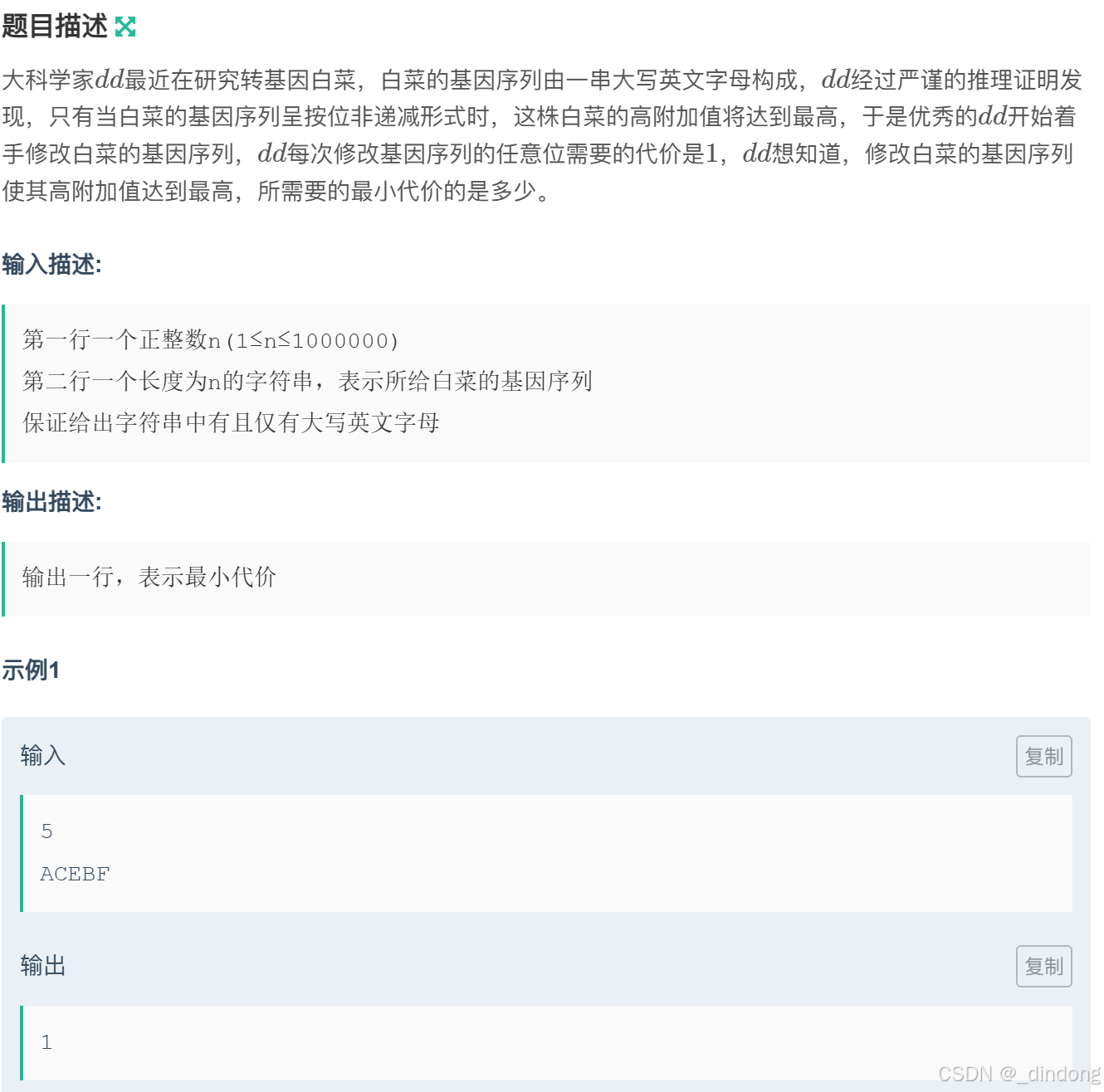
其实是查找最长递增子序列,记长度为L,答案为n-L
可以用动规做,最优解法是贪心+二分
cpp
#include<iostream>
#include<vector>
using namespace std;
string s;
int n;
//最长非下降子序列
int main(){
cin>>n>>s;
vector<char> v;
for(int i=0;i<n;++i){
char ch=s[i];
if(v.size()==0||ch>=v.back()) v.emplace_back(ch);
else{
//开始二分
int left=0,right=v.size()-1;
while(left<right){
int mid=left+(right-left)/2;
if(v[mid]<=ch) left=mid+1;
else right=mid;
}
v[left]=ch;
}
}
cout<<n-v.size()<<endl;
return 0;
}七、kanan和高音(双指针)
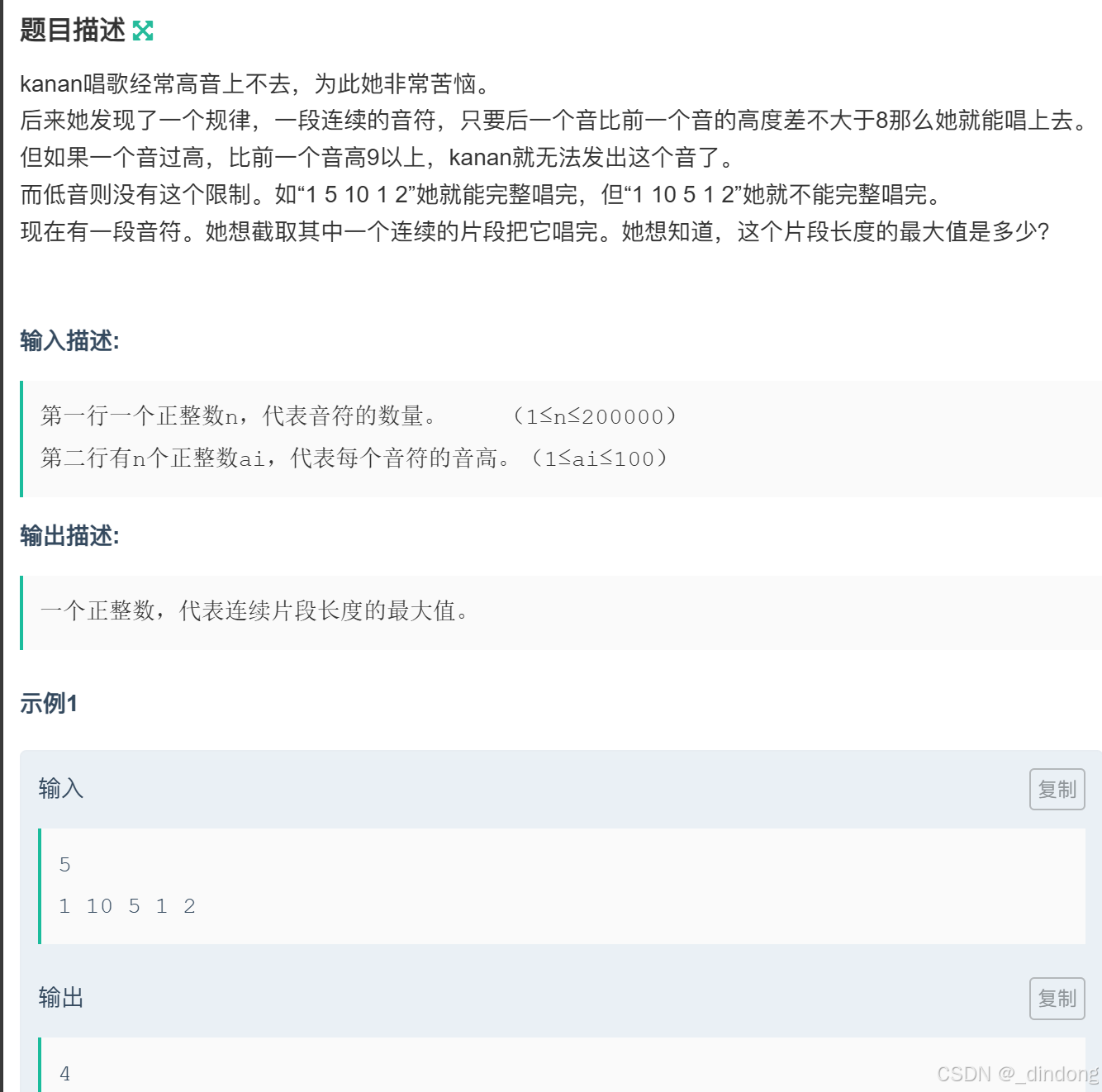
cpp
#include <iostream>
using namespace std;
const int N=2e5+10;
int n,arr[N];
int main() {
cin>>n;
for(int i=0;i<n;++i)cin>>arr[i];
int len=1,left=0,right=0;
while(right<n)
{
while(right+1<n&&arr[right+1]-arr[right]<9)++right;
len=max(len,right-left+1);
++right;
left=right;
}
cout<<len;
return 0;
}八、拜访(单源bfs最短路)

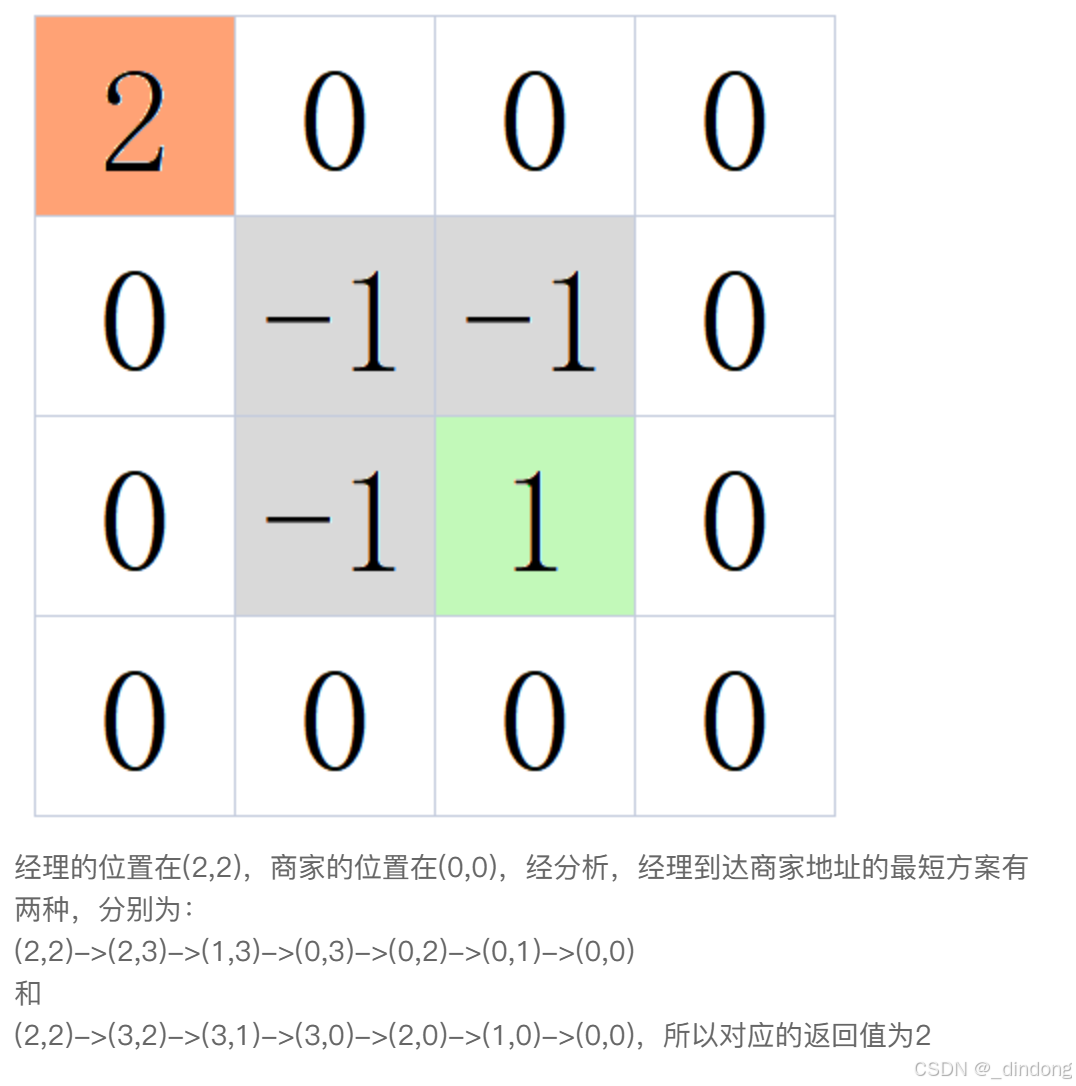

cpp
#include <vector>
class Solution {
private:
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
public:
int countPath(vector<vector<int> >& CityMap, int n, int m) {
queue<pair<int,int>> q;
for(int i=0;i<n;++i)
{
bool flag=false;
for(int j=0;j<m;++j)
{
if(CityMap[i][j]==1)
{
q.push({i,j});
flag=true;
break;
}
}
if(flag)break;
}
int ret=0;
vector<vector<bool>> vis(n,vector<bool>(m));
while(!q.empty())
{
//记录此层元素个数
int sz=q.size();
bool flag=false;
while(sz--)
{
auto [i,j]=q.front();
q.pop();
//标记已经经过的地方
vis[i][j]=true;
for(int k=0;k<4;++k)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<n&&y>=0&&y<m&&CityMap[x][y]!=-1&&!vis[x][y])
{
if(CityMap[x][y]==2)
{
//此时是最短路线,等待此层其他能到达的,统计
++ret;
flag=true;
//中断该点的探查
break;
}
q.push({x,y});
}
}
}
//找到了最短路线,退出
if(flag)break;
}
return ret;
}
};九*、买卖股票的最佳时机IV(多状态dp,"k次交易"注意初始化)


cpp
#include <iostream>
#include<vector>
using namespace std;
const int N=1010;
int n,k,prices[N];
int main() {
cin>>n>>k;
for(int i=1;i<=n;++i)cin>>prices[i];
//f买入 g可交易
vector<vector<int>> f(n+1,vector<int>(k+1));
auto g=f;
int money=0;
for (int j=0;j<=k-1;++j)f[0][j]=-prices[1];
for(int i=1;i<=n;++i)
{
for(int j=0;j<=k;++j)
{
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
g[i][j]=g[i-1][j];
if(j>=1)g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
}
}
for(int j=1;j<=k;++j)money=max(money,g[n][j]);
cout<<money;
return 0;
}十、AOE还是单体?(贪心)
cpp
#include<iostream>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int arr[N];
int n,x;
int main(){
cin>>n>>x;
for(int i=1;i<=n;++i) cin>>arr[i];
sort(arr+1,arr+1+n);
long long ret=0;
int index=max(n-x,0);
ret+=arr[index]*x;
for(int i=index+1;i<=n;++i) ret+=arr[i]-arr[index];
cout<<ret<<endl;
return 0;
}十一、kotori和n皇后(哈希)

N皇后经典的就是判断条件hh
cpp
#include <iostream>
#include<unordered_map>
using namespace std;
using ll=long long;
const int M=1e5+10;
int k,x,y,t,i;
int main() {
//Dig1主对角线 Dig2副对角线
unordered_map<ll,int> R,C,Dig1,Dig2;
cin>>k;
int flag=M,cnt=1;
while(cnt<=k)
{
cin>>x>>y;
//因为还要输入,不能找到后直接break
if (flag!=M)
{
++cnt;
continue;
}
if(R.count(x)||C.count(y)||Dig1.count(y-x)||Dig2.count(y+x))
{
//寻找第一次出现冲突的那一个,后边冲突一直存在
flag=cnt;
}
++R[x],++C[y],++Dig1[y-x],++Dig2[y+x];
++cnt;
}
cin>>t;
while(t--)
{
cin>>i;
if(i<flag)cout<<"No";
else cout<<"Yes";
cout<<'\n';
}
return 0;
}十二**、取金币(区间dp)

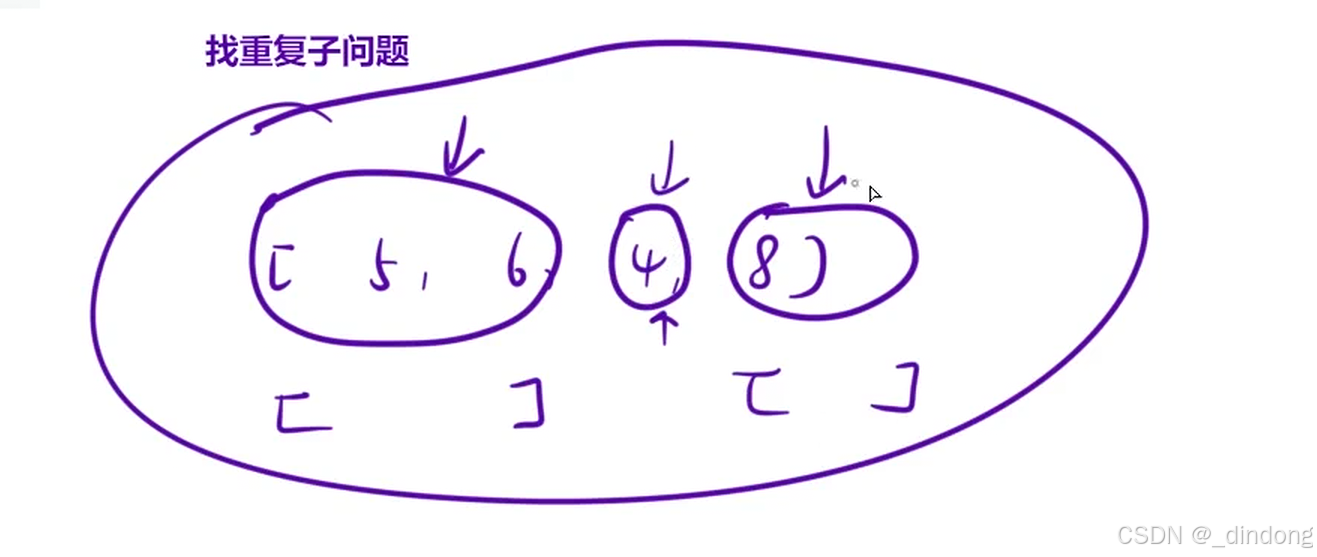
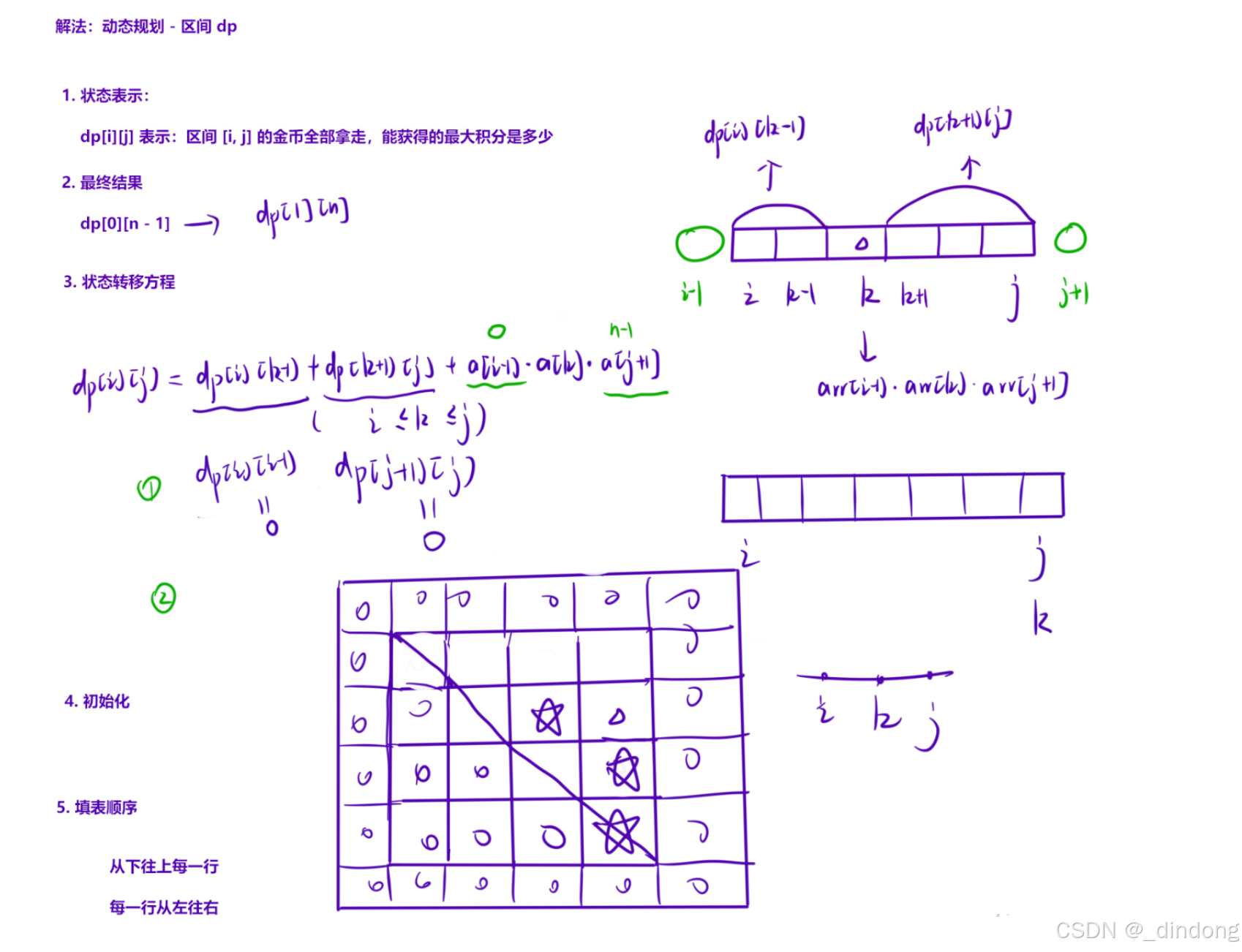
cpp
class Solution {
public:
int arr[110]={0};
int dp[110][110]={0};
int getCoins(vector<int>& coins) {
//dp[i][j] i-j区间的最大积分
int n=coins.size();
arr[0]=arr[n+1]=1;
for(int i=1;i<=n;++i) arr[i]=coins[i-1];
for(int i=n;i>=1;--i)
for(int j=i;j<=n;++j)
for(int k=i;k<=j;++k)
dp[i][j]=max(dp[i][j],dp[i][k-1]+dp[k+1][j]+arr[k]*arr[i-1]*arr[j+1]);
return dp[1][n];
}
return 0;
};十三、矩阵转置


修改输出逻辑即可
cpp
#include <iostream>
using namespace std;
int arr[15][15];
int main() {
int n,m;
cin>>n>>m;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)cin>>arr[i][j];
for(int j=0;j<m;++j)
{
for(int i=0;i<n-1;++i)
{
cout<<arr[i][j]<<" ";
}
cout<<arr[n-1][j]<<"\n";
}
return 0;
}十四**、四个选项(枚举+dfs+剪枝+哈希)
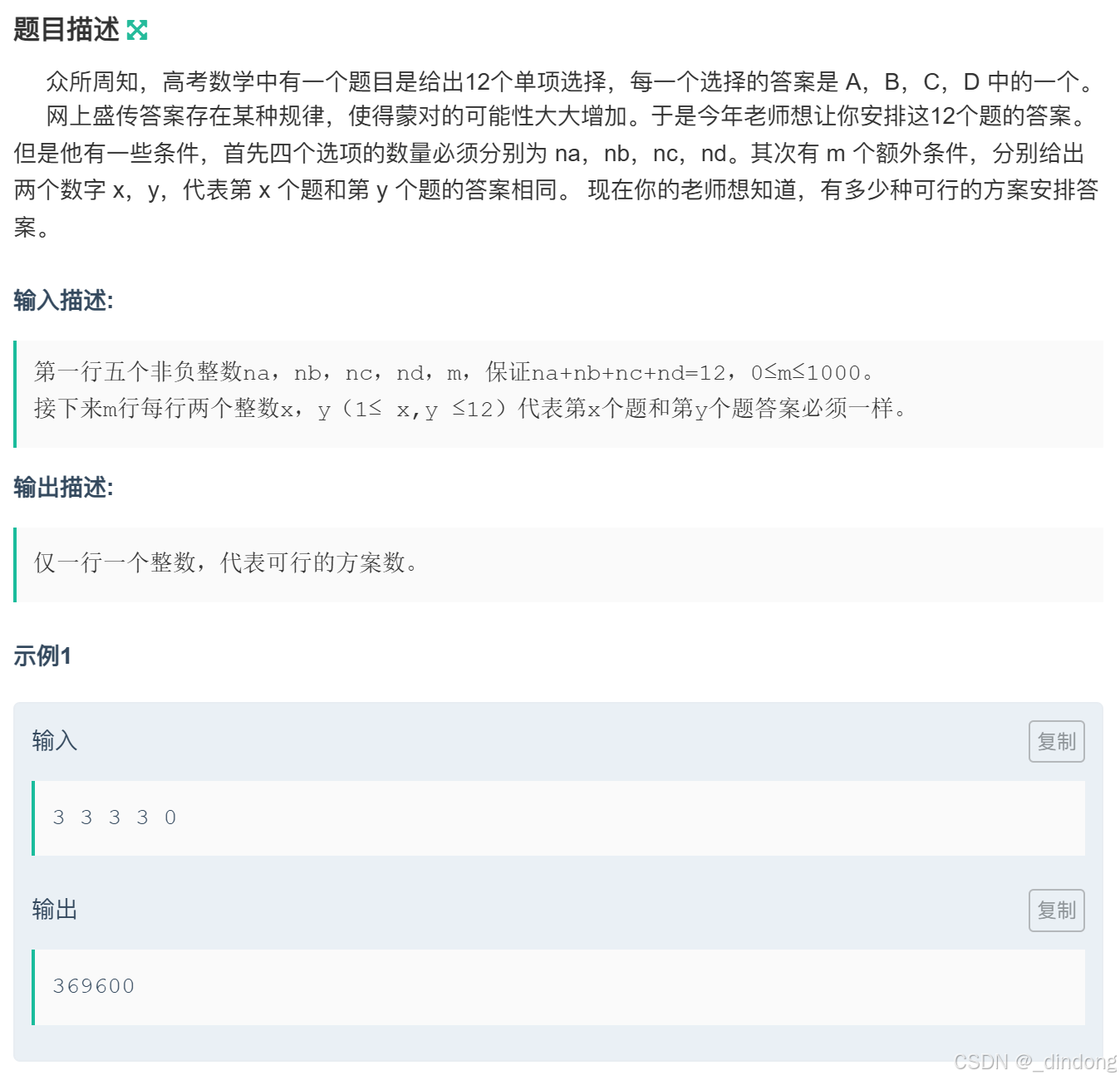
dfs题并不难,考察的是编码能力
cpp
#include<iostream>
#include<vector>
using namespace std;
int m,x,y;
bool same[13][13];//标记两题的选项是否相同
int ret=0;
int cnt[5];//记录每个选项的次数
vector<int> path;//记录过程中已经选过了哪些选项 1-12号位置分别代表1-12题 1-4分别代表具体选项
bool issame(int pos,int cur){//pos代表之前的位置 cur是我们期望填入的选项
for(int i=1;i<pos;++i)
if(same[pos][i]&&path[i]!=cur) return false;
return true;
}
void dfs(int pos){
if(pos>12){
++ret;
return;
}
//此时开始尝试填选项
for(int i=1;i<=4;++i)
if(cnt[i]&&issame(pos,i)){
path.emplace_back(i);
--cnt[i];
dfs(pos+1);
path.pop_back();
++cnt[i];
}
}
int main(){
for(int i=1;i<=4;++i) cin>>cnt[i];
cin>>m;
while(m--){
cin>>x>>y;
same[x][y]=same[y][x]=true;//表示两个选项必须相同
}
path.emplace_back(0);//占位置
dfs(1);
cout<<ret<<endl;
return;
}十五、接雨水(双指针)

左右指针,记录更小的,更小为始往中间逼近,遇到比记录的小值小的,+=差值,否则更新小值,进入下一轮,直到指针相遇
cpp
class Solution {
public:
int trap(vector<int>& arr) {
int n=arr.size();
if(n<=2)return 0;
int right=n-1,left=0,ret=0;
while(left<right)
{
if(arr[left]<arr[right])
{
int tmp=arr[left];
while(arr[left+1]<tmp)
{
ret+=(tmp-arr[left+1]);
++left;
}
//arr[left+1]>tmp更新端点
++left;
}
else{
int tmp=arr[right];
while(arr[right-1]<tmp)
{
ret+=(tmp-arr[right-1]);
--right;
}
--right;
}
}
return ret;
}
};十六、疯狂的自我检索者(贪心)

cpp
#include <iostream>
#include<iomanip>
using namespace std;
int n,m,x;
int main() {
cin>>n>>m;
double ans=0;
for(int i=0;i<n-m;++i)
{
cin>>x;
ans+=x;
}
double tmp=ans;
for(int i=0;i<m;++i)ans+=1;
cout<<fixed<<setprecision(5)<<ans/n<<" ";
ans=tmp;
for(int i=0;i<m;++i)ans+=5;
cout<<fixed<<setprecision(5)<<ans/n;
return 0;
}十七、栈和排序(贪心+栈)


cpp
class Solution {
public:
vector<int> solve(vector<int>& a) {
vector<int> ret;
int n=a.size();
if(n==0)return ret;
int cur=0;
stack<int> st;
while(ret.empty()&&a[cur]!=n)
{
st.push(a[cur]);
++cur;
}
ret.push_back(a[cur]);
++cur;
while(cur<n)
{
int max_num=st.empty()?0:st.top();
for(int i=cur;i<n;++i)max_num=max(max_num,a[i]);
while(cur<n&&(st.empty()||st.top()!=max_num))
{
st.push(a[cur++]);
}
ret.push_back(st.top());
st.pop();
}
while(!st.empty())
{
ret.push_back(st.top());
st.pop();
}
return ret;
}
};十八**、加减(排序+贪心+滑动窗口)
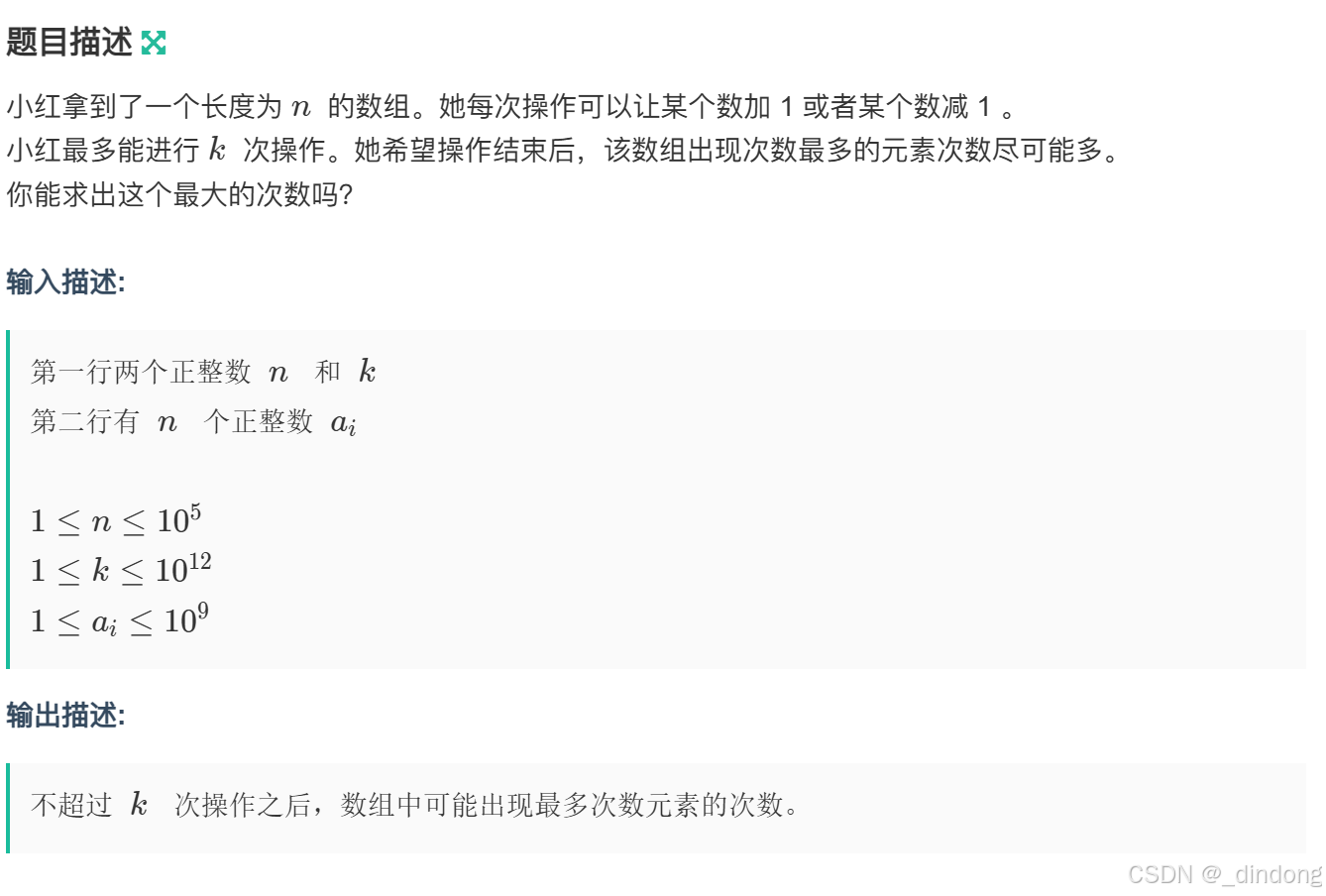

难在滑动窗口的更新条件,综合起来看是很好的一道题了

cpp
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
typedef long long LL;
LL n,k,arr[N],sum[N]; // sum是前缀和数组
LL cal(int left,int right){
//这个函数统计把该区间都变成相同的最小代价
int mid=(left+right)>>1;
return (mid-left-right+mid)*arr[mid]-(sum[mid-1]-sum[left-1])+(sum[right]-sum[mid]);
}
int main(){
cin>>n>>k;
for(int i=1;i<=n;++i) cin>>arr[i];
//排序+前缀和数组的预处理
sort(arr+1,arr+1+n);
for(int i=1;i<=n;++i) sum[i]=sum[i-1]+arr[i];
int ret=1;
for(int left=1,right=1;right<=n;++right){
while(cal(left,right)>k) ++left;
ret=max(ret,right-left+1);
}
cout<<ret;
return 0;
}至此,笔试强训全部结束。