机器学习009:监督学习【回归算法】（岭回归）-- 给模型一个“清醒”的约束

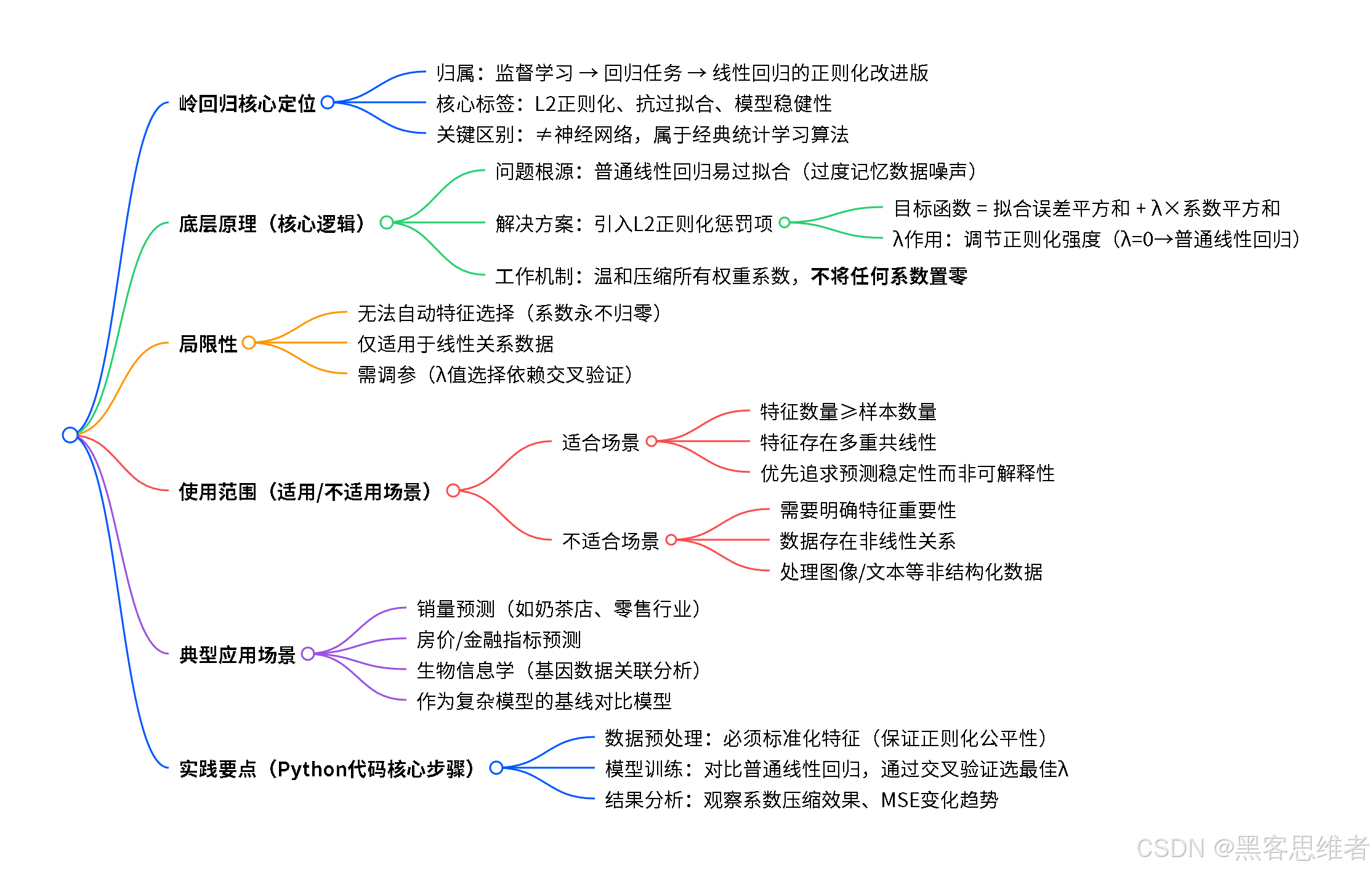
想象一下，你想预测下周奶茶店的销量，考虑了天气、温度、星期几、促销活动甚至店长的星座等十几个因素。结果模型在历史数据上"学"得太好，把噪音都记住了，对未来预测却一塌糊涂。这时，你需要一位"教练"给模型套上"缰绳"，让它更稳健。这个"教练"就是岭回归。

一、当模型"学过头"了怎么办？

今天我们要聊的不是一个复杂的"神经网络"，而是一个非常实用、在机器学习领域里扮演着"稳定器"角色的经典算法------岭回归。它就像一个经验丰富的老师，不是教你记下所有题目，而是教你抓住解题的核心思路。

首先，破除一个常见的误解 ：你可能在很多地方看到"岭回归算法"这个词。但严格来说，岭回归并不属于"神经网络"家族 。它更古老、更经典，属于"统计学习"和"机器学习"中回归算法 这个大类，是 线性回归 的一个非常重要的改进版本。

用一个生活场景来理解它的重要性：假设你是奶茶店长，想根据历史数据预测明天的销量。你开始收集影响因素：天气（晴/雨/阴）、温度、星期几、是否有促销、节假日、附近学校是否放假、甚至当天热搜榜上有没有奶茶相关话题......你用这些数据训练了一个预测模型（比如一个复杂的线性模型）。

几天后你发现，这个模型对过去的数据 预测得分非常高，几乎分毫不差，但用它来预测未来时，却错得离谱。为什么？因为它过于努力地去"迎合"或"记忆"历史数据中的每一个细节，包括那些偶然的、没有规律的波动（我们称之为"噪声"）。这就好比一个学生，为了应付考试，把练习题的标准答案一字不差地背下来，却没有理解背后的原理，一旦题目稍有变化，就束手无策了。

这种现象在机器学习中被称为 "过拟合" 。而岭回归，就是为了解决这个问题而生的。它给原本"自由奔放"的线性模型加上了一个巧妙的约束，就像一个"清醒剂"，让模型在拟合数据和保持简洁之间找到一个最佳平衡点。

二、分类归属：它到底属于哪门哪派？

为了方便大家理解岭回归在整个AI世界中的位置，我们先来画一张简单的地图：
机器学习算法监督学习无监督学习分类任务回归任务线性回归岭回归套索回归弹性网络核心特点:L2正则化目标:防止过拟合,提高泛化能力

让我们从上图来定位岭回归：

按功能用途划分 ：它属于监督学习 下的回归任务 。它的核心使命是根据已有的、带标签的数据（例如：过去30天每一天的销量和对应的天气、温度），去预测一个连续数值（例如：明天的具体销量是123杯，而不是"好/中/差"这类类别）。
按模型特性划分 ：它是 线性回归的"正则化"改进版。你可以把它理解为线性回归家族中的"大哥哥"，它继承了线性回归所有简单、直观的优点，同时又增加了一个防止弟弟（基础线性回归）"学坏"（过拟合）的"家规"（正则化）。

所以，一句话总结 ：岭回归是一种带有L2正则化项的线性回归模型 ，专门用于解决回归预测 问题，其核心价值在于通过增加一个惩罚机制 来提升模型的稳定性和泛化能力。泛化能力，就是模型在没见过的新数据上也能表现良好的能力。

三、底层原理：给模型套上"缰绳"的艺术

理解岭回归，我们分三步走：先看它要解决的问题（普通线性回归的毛病），再看它的解决方案（惩罚项），最后理解它是如何工作的。

第一步：问题起源------自由奔跑的"基础线性回归"

类比：想象你在教一个刚学画画的孩子画人脸。你给他看了100张不同的人脸照片。你希望他学会人脸的基本规律：两只眼睛、一个鼻子、一张嘴。
普通线性回归 就像这个孩子，他的目标是让自己画的画，和你看过的这100张照片尽可能像 。为了达到这个目标，他可能会给某张照片上的一个小雀斑、一根翘起来的头发都画得一模一样。这样，对这100张照片的"还原度"得分（专业术语叫训练误差）非常高。

但你带他去户外写生，画一个真实的人时，问题来了。因为他记住了太多不必要的细节，反而画不出一个正常、简洁的人脸，可能会把别人脸上没有的雀斑也画上去。这就是过拟合。

数学上的简单描述（可略过，不影响理解逻辑） ：

普通线性回归的目标是找到一组系数（也叫权重或参数，记作 w1， w2， ...），让下面这个公式的值最小化 ：
Loss = (预测值 - 真实值)² 的总和

它只关心一个目标：让预测结果和历史数据无限接近，为此它愿意把系数调整得非常大，去"硬凑"那些偶然的数据点。

第二步：解决方案------引入"清醒剂"L2正则化

类比：现在，你给孩子定了一条新规矩："宝贝，你可以自由地画，但是画得太复杂、用笔太重的话，我会扣你的小红花。"这里的"用笔太重"和"画得太复杂"，就对应着模型系数 w 的绝对值太大。

岭回归就是给模型加上了这条"规矩"，这条规矩的专业名称叫 L2正则化项。它的目标函数变成了：

复制代码

新的目标 = (预测值 - 真实值)² 的总和 + λ * (w1² + w2² + ... + wn²)

这个公式里出现了两个部分：

第一部分：和原来一样，要求"预测要准"。这叫"拟合数据"。
第二部分（关键！） ：λ * (所有系数平方和)。这叫惩罚项。

λ (念作"拉姆达")：一个超参数，你可以理解为"规矩的严格程度"。λ=0，就是没规矩，变回普通线性回归；λ 越大，规矩越严，对"大系数"的惩罚就越重。
系数平方和：衡量了模型的"复杂程度"。系数越大（无论是正还是负），模型就越"敏感"，越容易去捕捉那些微小的、可能是噪声的变化。

核心逻辑 ：岭回归不再只追求"预测准"，而是要在 "预测得准" 和 "模型保持简洁、系数别太大" 之间，找一个最佳的妥协点。λ 就是这个平衡的调节旋钮。

第三步：如何工作------温和的压缩

类比：岭回归的惩罚方式非常"温和"。它像一个和蔼的教练，对所有特征的系数说："大家都要注意，不要膨胀。如果你已经很大了，我让你缩小一点；如果你本身就不大，那影响也很小。"它是整体性、均匀地压缩所有系数 ，但永远不会把任何一个系数压缩到绝对的0。

这意味着什么呢？意味着即使是一个非常不重要的特征（比如"店长的星座"），在岭回归模型里，它也会有一个非常非常小、但不是零的系数。模型保留了它，但认为它对最终预测的贡献微乎其微。

这个过程我们用一个简单的图示来理解模型参数（系数）的变化：

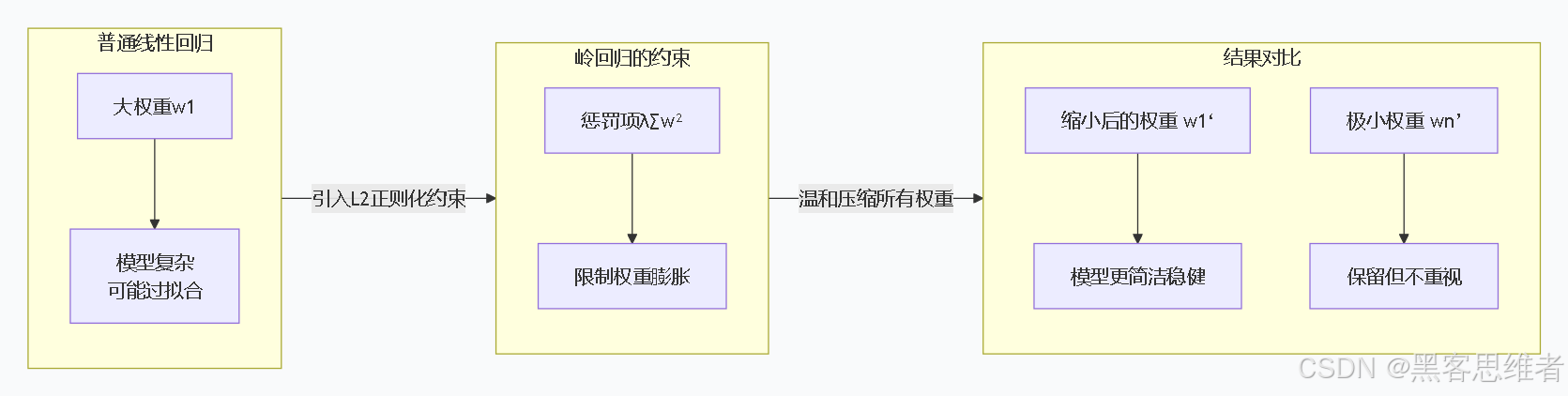
上图的逻辑是：岭回归通过惩罚项，对普通线性回归中可能过大的权重进行整体性的、温和的压缩，从而得到一个更稳定、更不易过拟合的模型。

四、局限性：它不是"万能药"

了解了岭回归的强大，我们必须客观地看到它的边界。没有一种算法是完美的，岭回归也不例外。

不能做自动特征选择 ：这是岭回归与它的"兄弟"------套索回归 最大的区别。如前所述，岭回归对所有系数一视同仁地进行温和压缩，不会将任何特征的系数完全变成0。这意味着，即使某个特征完全没用，它也会留在模型里，只是系数非常小。在需要模型可解释性，或者明确想知道"哪些特征是关键"的场景下，岭回归的这个特性就是个缺点。
假设关系是线性的 ：岭回归的核心仍是线性模型 。它假设我们要预测的目标（如销量）和各个特征（天气、温度等）之间，存在一种加权求和的线性关系。如果真实世界中的关系非常复杂，是曲线、跳跃式或者有复杂的交互作用，那么岭回归的表现可能会不尽如人意。它就像一个只会用直尺画图的画家，面对弯曲的线条时就力不从心了。
需要调参 (λ的选择) ：虽然λ给了我们调节模型复杂度的能力，但如何选择最佳的λ值，本身就是一个需要技巧和经验的步骤（通常通过交叉验证来完成）。这多了一个步骤，对于追求完全自动化部署的场景来说，是一个小小的负担。

简单总结其局限 ：岭回归是一个优秀的线性、稳健 的回归器，但它不擅长在复杂非线性关系中工作，也无法自动告诉我们哪些特征更重要。

五、使用范围：何时该请它出马？

基于它的原理和局限性，我们可以清晰地划定岭回归的"能力圈"：

适合用岭回归解决的问题：

特征数量多，甚至多于样本数量：比如，你只有过去100天的销售数据（100个样本），但却考虑了200个可能的影响因素（200个特征）。普通线性回归在这种情况下极易过拟合，而岭回归的正则化惩罚正好可以约束模型。
特征之间存在多重共线性：这是岭回归最经典的应用场景。共线性是指特征之间高度相关，比如预测房价时，"房屋面积"和"房间数量"通常是相关的。这种相关性会让普通线性回归的系数估计变得非常不稳定（像一个跷跷板，很难确定功劳归谁）。岭回归通过压缩系数，能有效稳定这种估计。
首要目标是获得稳定的预测，而非解释模型：当你更关心"预测得准不准"，而不是"到底是哪个因素在起作用"时，岭回归的稳健性优势就体现出来了。

不适合用岭回归解决的问题：

需要明确特征重要性的场景：如果你想从模型中知道"促销活动"和"温度"哪个对销量影响更大，套索回归或树模型（如随机森林）可能是更好的选择。
数据中存在明显的非线性关系：如果销量和温度的关系是"太冷没人买，太热也没人买，20-25度时销量暴增"这种抛物线关系，那么你应该考虑使用多项式回归、支持向量机或神经网络等能捕捉非线性的模型。
处理图像、声音、文本等非结构化数据：这类数据特征间的关系极其复杂，传统线性模型（包括岭回归）基本无能为力，需要CNN、RNN等专门的深度学习模型。

六、应用场景：它在我们身边

岭回归虽然"古老"，但在众多需要稳定预测的领域，依然扮演着基石角色。

房价预测：这是教科书级的案例。预测房价时，特征包括面积、房间数、地段评分、房龄、周边学校数量等。这些特征之间往往存在共线性（大房子通常房间也多），且我们最终需要一个具体的预测价格。房地产平台或银行的自动估价系统，其底层算法很可能就集成了岭回归这类正则化线性模型，以保证在不同区域、不同房型上都能给出相对稳健的估价。
金融与经济指标预测：比如预测某支股票的收益率、预测下一季度的GDP增长率。分析师会考虑数十甚至上百个宏观经济指标（利率、通胀率、PMI、失业率等），这些指标高度相关且数量可能多于历史数据期数。岭回归能有效处理这种"宽数据"，提供更可靠的风险和趋势评估。
销量与需求预测：回到我们开篇的奶茶店例子。对于连锁零售、快消品行业，预测未来销量是核心任务。岭回归可以帮助企业平衡各种促销活动、季节性因素、竞品行为等多重因素的影响，做出更合理的库存管理和生产计划，避免缺货或积压。
生物信息学与疾病风险预测：在基因研究中，科学家可能拥有成千上万个基因表达数据（特征），但只有几百个病人样本（样本）。他们想找出哪些基因与某种疾病相关（连续指标，如风险分数）。岭回归可以在这种情况下提供稳定的关联性分析，虽然不能直接做特征选择，但其系数的相对大小也能提供一些线索。
任何线性模型的"增强底座" ：在很多复杂的机器学习系统或学术研究中，岭回归常常作为基线模型出现。研究员会先用岭回归跑出一个结果，再用更复杂的模型（如XGBoost、神经网络）去尝试超越它。如果复杂模型连这个"稳健的线性基准"都无法显著超越，那其复杂性可能就是不必要的。

七、动手实践：Python代码案例

理论讲完，我们来点实际的。下面是一个使用Python的scikit-learn库实现岭回归预测波士顿房价（经典数据集）的简单示例。我会加上详细注释，哪怕你是第一次接触代码也能看懂逻辑。

python 复制代码

# 导入必要的工具库
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing  # 使用加州房价数据集，更常用
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# 1. 加载数据
print("步骤1： 加载加州房价数据集...")
housing = fetch_california_housing()
X = housing.data  # 特征数据，比如收入、房龄、房间数等
y = housing.target # 目标数据，即房屋价格中位数
feature_names = housing.feature_names

print(f"数据集形状: 样本数 {X.shape[0]}, 特征数 {X.shape[1]}")
print(f"特征名: {feature_names}")

# 2. 数据预处理：标准化（非常重要！让所有特征处于同一尺度，方便正则化公平作用）
print("\n步骤2： 对特征数据进行标准化处理...")
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 计算均值和标准差，并进行转换

# 3. 划分训练集和测试集（用70%的数据训练，30%的数据测试模型效果）
print("\n步骤3： 划分训练集和测试集...")
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)
print(f"训练集大小: {X_train.shape}, 测试集大小: {X_test.shape}")

# 4. 训练普通线性回归模型作为对比基线
print("\n步骤4： 训练普通线性回归模型...")
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred_lr = lr.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_lr)
print(f"普通线性回归 - 测试集均方误差(MSE): {mse_lr:.4f}")

# 5. 训练岭回归模型
print("\n步骤5： 训练岭回归模型...")
# 尝试不同的 alpha (即我们前面说的 λ) 值，看看效果
alphas = [0.001, 0.01, 0.1, 1, 10, 100, 1000]
ridge_mse = []
best_ridge = None
best_score = float('inf')
best_alpha = 0

print("尝试不同的正则化强度(alpha值):")
for alpha in alphas:
    ridge = Ridge(alpha=alpha, random_state=42)
    ridge.fit(X_train, y_train)
    y_pred_ridge = ridge.predict(X_test)
    mse_ridge = mean_squared_error(y_test, y_pred_ridge)
    ridge_mse.append(mse_ridge)
    
    # 使用交叉验证在训练集上评估模型的稳健性（更可靠）
    cv_scores = -cross_val_score(ridge, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
    avg_cv_mse = np.mean(cv_scores)
    
    print(f"  alpha={alpha:7.3f} | 测试集MSE: {mse_ridge:.4f} | 交叉验证平均MSE: {avg_cv_mse:.4f}")
    
    if avg_cv_mse < best_score:
        best_score = avg_cv_mse
        best_alpha = alpha
        best_ridge = ridge

print(f"\n最佳的正则化强度 alpha = {best_alpha}")

# 6. 结果对比与可视化
print("\n步骤6： 结果对比...")
print(f"普通线性回归测试集MSE: {mse_lr:.4f}")
print(f"岭回归(alpha={best_alpha})测试集MSE: {mean_squared_error(y_test, best_ridge.predict(X_test)):.4f}")

# 对比模型系数（权重）
coef_comparison = pd.DataFrame({
    '特征': feature_names,
    '线性回归系数': lr.coef_,
    f'岭回归系数(alpha={best_alpha})': best_ridge.coef_
})
print("\n模型系数对比（注意岭回归系数被'压缩'得更小）:")
print(coef_comparison.to_string(index=False))

# 7. 绘制MSE随alpha变化的曲线
plt.figure(figsize=(10, 6))
plt.plot(alphas, ridge_mse, 'o-', linewidth=2, label='测试集MSE')
plt.axhline(y=mse_lr, color='r', linestyle='--', label='线性回归MSE')
plt.xscale('log')  # 因为alpha变化范围大，用对数坐标更清晰
plt.xlabel('正则化强度 alpha (λ) - 对数坐标')
plt.ylabel('均方误差 (MSE)')
plt.title('岭回归：不同正则化强度下的模型性能')
plt.legend()
plt.grid(True, which="both", ls="--")
plt.show()

print("\n实践小结：")
print("1. 通过对比MSE，你可以看到合适的alpha值能让岭回归取得比普通线性回归更优（或相当）的预测误差。")
print("2. 观察'模型系数对比'表格，你会发现岭回归的系数绝对值普遍比线性回归的小，这就是'压缩'效果。")
print("3. 曲线图展示了alpha的作用：太小接近线性回归，太大会导致'欠拟合'（误差上升），中间存在一个最优值。")

运行这段代码，你将直观地看到：

岭回归如何通过调整alpha（λ）来影响预测精度。
岭回归的系数是如何被"温和压缩"的。
如何通过交叉验证寻找最佳的超参数。

总结：岭回归的核心价值

岭回归可能不是AI领域最闪耀的明星，但绝对是最值得信赖的基石之一 。它的核心价值在于，用一种优雅而简单的数学方法（L2正则化），赋予了线性模型抵抗"过拟合"的能力，使其在面对复杂、多特征、带噪声的真实世界数据时，表现出卓越的稳健性和泛化能力。