文章目录
- [一. 力扣 [647. 回文子串](https://leetcode.cn/problems/palindromic-substrings/description/)](#一. 力扣 647. 回文子串)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [二. 力扣 [5. 最长回文子串](https://leetcode.cn/problems/longest-palindromic-substring/description/)](#二. 力扣 5. 最长回文子串)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [三. 力扣 [1745. 分割回文串 IV](https://leetcode.cn/problems/palindrome-partitioning-iv/description/)](#三. 力扣 1745. 分割回文串 IV)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [四. 力扣 [132. 分割回文串 II](https://leetcode.cn/problems/palindrome-partitioning-ii/description/)](#四. 力扣 132. 分割回文串 II)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [五. 力扣 [516. 最长回文子序列](https://leetcode.cn/problems/longest-palindromic-subsequence/description/)](#五. 力扣 516. 最长回文子序列)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [六. 力扣 [1312. 让字符串成为回文串的最少插入次数](https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/description/)](#六. 力扣 1312. 让字符串成为回文串的最少插入次数)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
一. 力扣 647. 回文子串
1. 题目解析
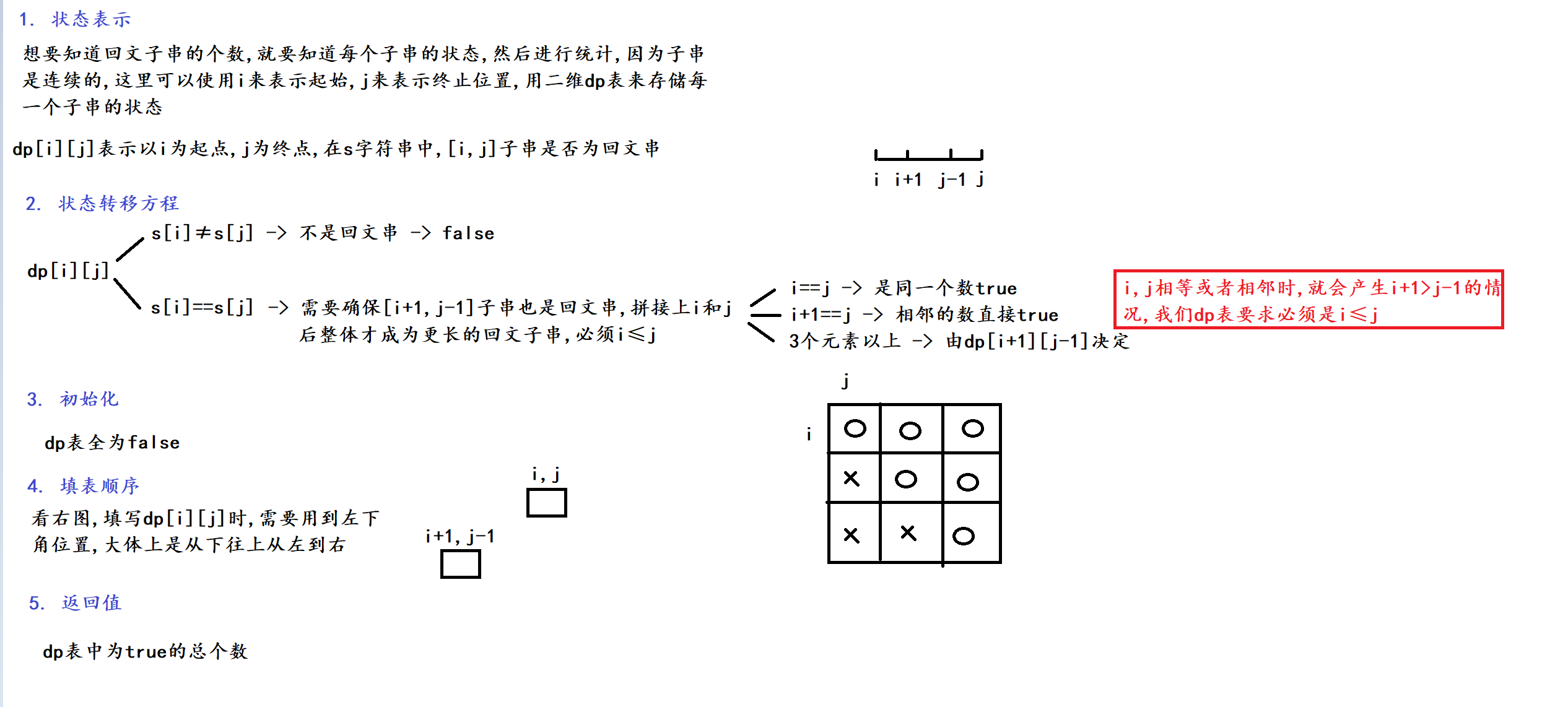
2. 算法原理
需要注意的点是填表顺序
3. 代码
java
class Solution {
public int countSubstrings(String ss) {
// 建表,初始化
char[] s = ss.toCharArray();
int n = s.length;
boolean[][] dp = new boolean[n][n];
// 填表
int ret = 0;
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
if (i == j || i + 1 == j) {
dp[i][j] = true;
}else {
dp[i][j] = dp[i + 1][j - 1];
}
}
if (dp[i][j]) {
ret++;
}
}
}
return ret;
}
}二. 力扣 5. 最长回文子串
1. 题目解析
这里要注意返回的是子串的元素, 而不是长度
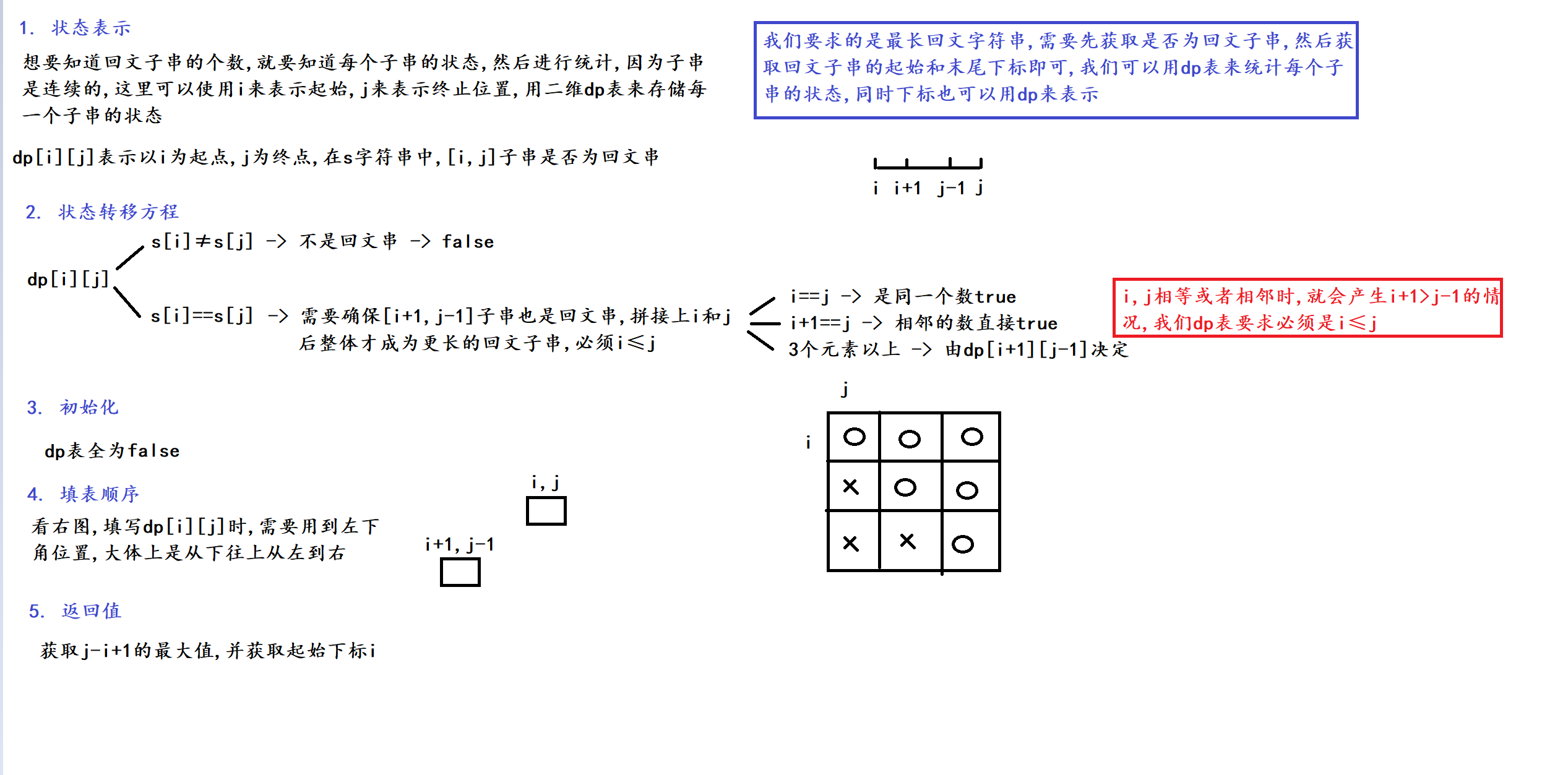
2. 算法原理
这道题和(回文子串)基本上原理一致, 只需要加上一步用来求最大长度和起始位置即可
3. 代码
java
class Solution {
public String longestPalindrome(String ss) {
// 建dp表
char[] s = ss.toCharArray();
int n = s.length;
boolean[][] dp = new boolean[n][n];
int start = 0;
int len = 0;
// 填dp表
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
}
if (dp[i][j]) {
if (j - i + 1 > len) {
len = j - i + 1;
start = i;
}
}
}
}
return ss.substring(start, start + len);
}
}三. 力扣 1745. 分割回文串 IV
1. 题目解析
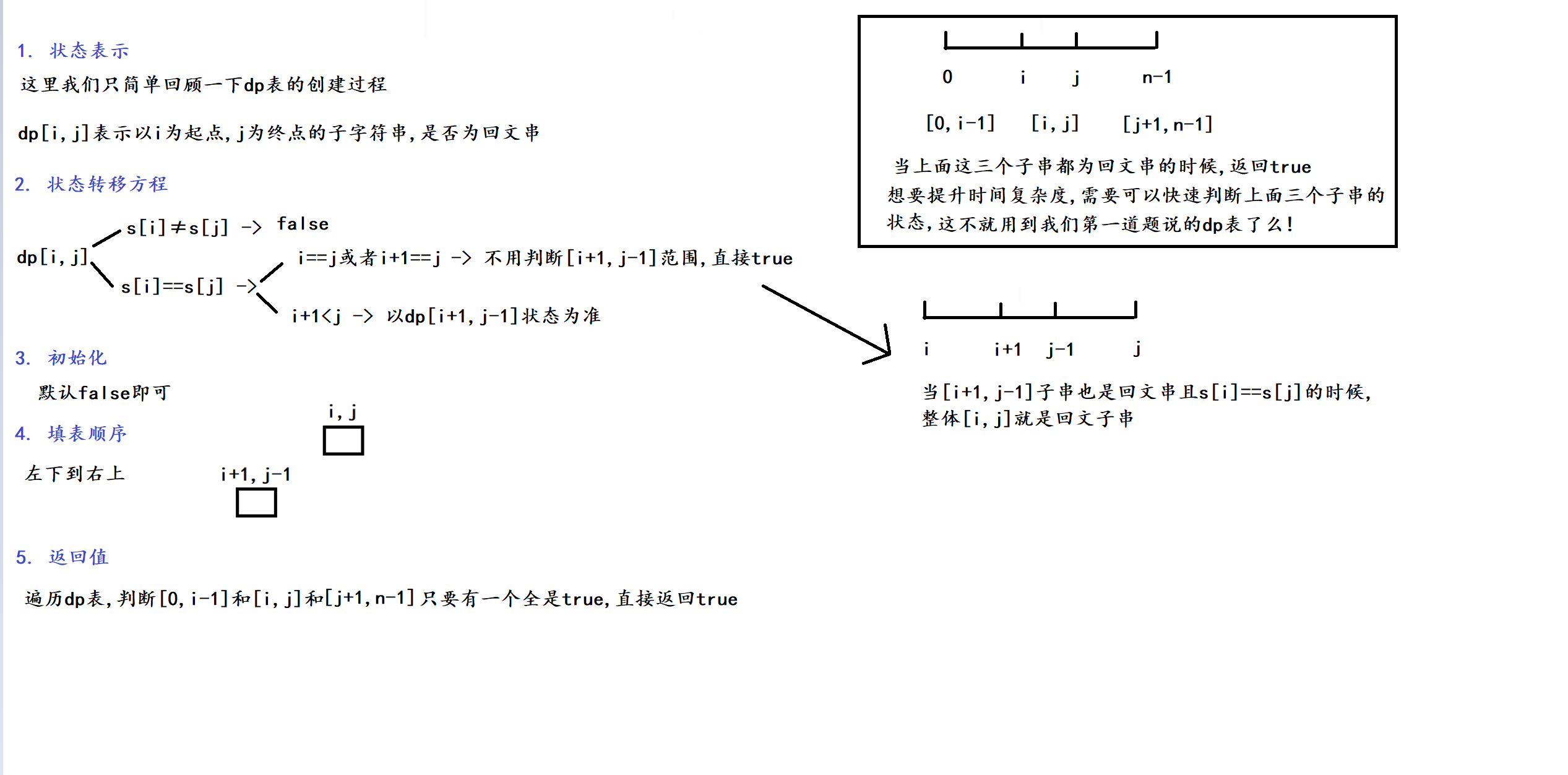
2. 算法原理
这道题和上面的题大体思想不变, 这里我们只简单回顾一下dp表的创建过程, 以及如何利用dp表来做这道题
3. 代码
java
class Solution {
public boolean checkPartitioning(String ss) {
// 建表
char[] s = ss.toCharArray();
int n = s.length;
boolean[][] dp = new boolean[n][n];
// 填表
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
}
}
}
// 再次遍历dp表, 开始分割
for (int i = 1; i < n - 1; i++) {
for (int j = i; j < n - 1; j++) {
if (i - 1 >= 0 && j + 1 <= n - 1) {
if (dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1]) {
return true;
}
}
}
}
return false;
}
}四. 力扣 132. 分割回文串 II
1. 题目解析
这道题上面那道题的进阶版本, 思路差不多一致
2. 算法原理
先用二维dp1表来存储每个子串状态, 再用新dp2表来求最小分割次数, 因为求dp1的过程我们已重复很多次, 因此这里省去这个过程
3. 代码
java
class Solution {
public int minCut(String ss) {
// 建表
char[] s = ss.toCharArray();
int n = s.length;
boolean[][] f = new boolean[n][n];
int[] dp = new int[n];
// 初始化
for (int i = 0; i < n; i++) {
dp[i] = 0x3f3f3f3f;
}
// 填f状态表
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
f[i][j] = i + 1 < j ? f[i + 1][j - 1] : true;
}
}
}
// 填dp表
for (int i = 0; i < n; i++) {
if (f[0][i]) {
dp[i] = 0;
}else {
for (int j = 1; j <= i; j++) {
if (f[j][i]) {
dp[i] = Math.min(dp[i], dp[j - 1] + 1);
}
}
}
}
return dp[n - 1];
}
}五. 力扣 516. 最长回文子序列
1. 题目解析
题干虽短, 但蕴含的信息很多
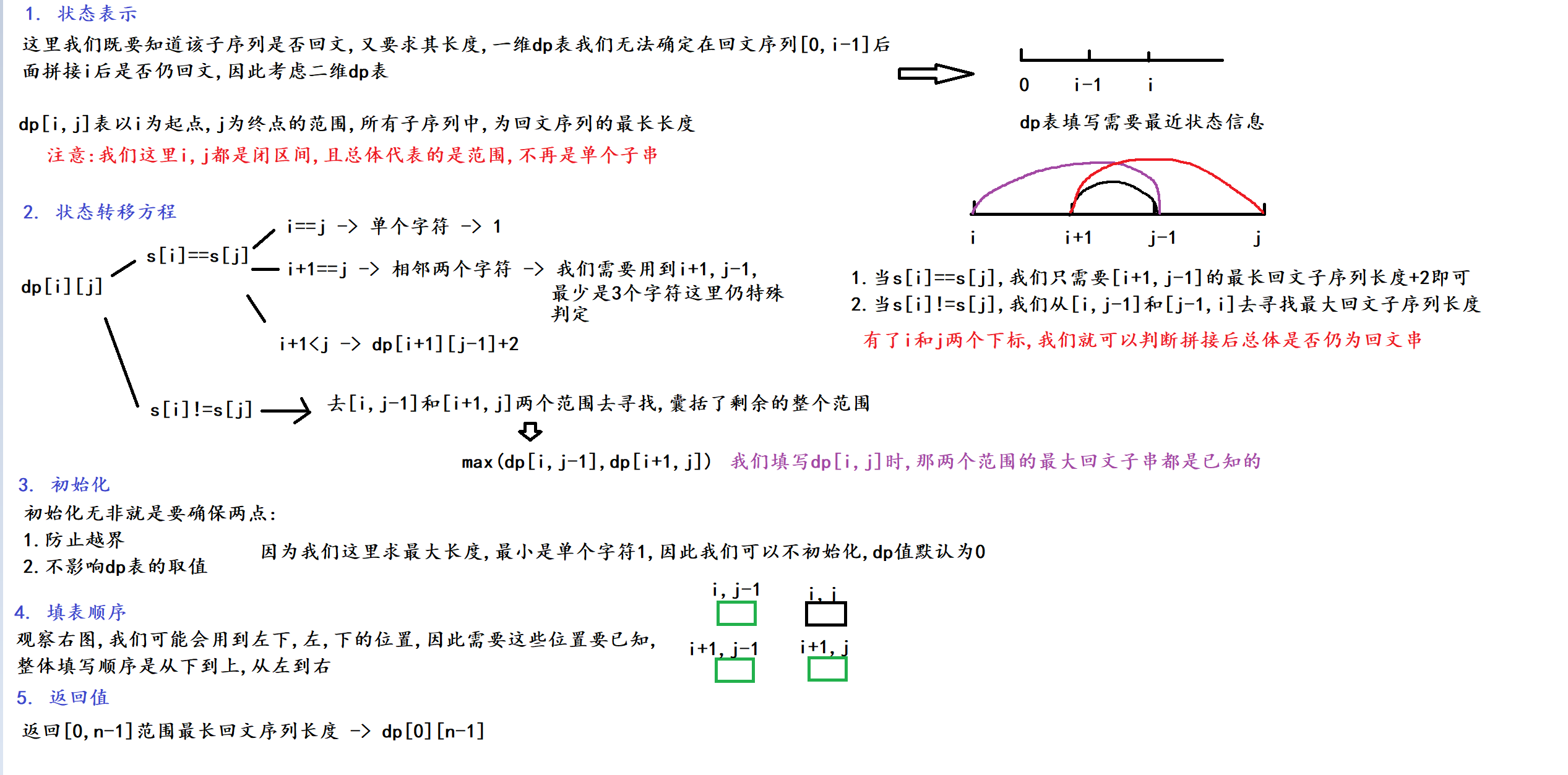
2. 算法原理
我们这里相当于遍历所有子串, 先求单个字符和两个字符的最大长度,再以此类推求整个范围, dp[i,j]是范围内所有子序列, 不是单个序列
3. 代码
java
class Solution {
public int longestPalindromeSubseq(String ss) {
// 建dp表,初始化
char[] s = ss.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
// 填dp表
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
if (i == j) {
dp[i][j] = 1;
}else if (i + 1 == j) {
dp[i][j] = 2;
}else {
dp[i][j] = dp[i + 1][j - 1] + 2;
}
}else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][n - 1];
}
}六. 力扣 1312. 让字符串成为回文串的最少插入次数
1. 题目解析
2. 算法原理
这里要注意的是dp[i,j]代表的含义, 这里代表的是单个子串, 而不是范围内的所有子串
3. 代码
java
class Solution {
public int minInsertions(String ss) {
// 建表
char[] s = ss.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
// 填表
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
if (s[i] == s[j]) {
if (i + 1 < j) {
dp[i][j] = dp[i + 1][j - 1];
}
}else {
dp[i][j] = Math.min(dp[i][j - 1], dp[i + 1][j]) + 1;
}
}
}
return dp[0][n - 1];
}
}