概念
解决回归问题的决策树模型你就是回归树
回归树是一种基于决策树的监督学习算法,用于解决回归问题。通过递归地将特征空间划分为多个子区域,并在每个子区域内拟合一个简单的预测值(如均值),实现对连续目标变量的预测。
特点
必须是二叉树
回归树的构建过程
-
特征选择与分割
遍历所有特征和可能的切分点,选择使均方误差(MSE)或平均绝对误差(MAE)最小的特征和切分点。
分割准则公式:
\\min_{j, s} \\left\[ \\min_{c_1} \\sum_{x_i \\in R_1(j,s)} (y_i - c_1)\^2 + \\min_{c_2} \\sum_{x_i \\in R_2(j,s)} (y_i - c_2)\^2 \\right\]
其中 ( R_1, R_2 ) 为分割后的子区域,( c_1, c_2 ) 为子区域内的预测值(通常取均值)。
-
递归分割
对每个子区域重复上述分割过程,直到满足停止条件(如最大深度、最小样本数或误差减少小于阈值)。
-
叶子节点预测
最终叶子节点的预测值为该区域内样本目标变量的均值。
举例:

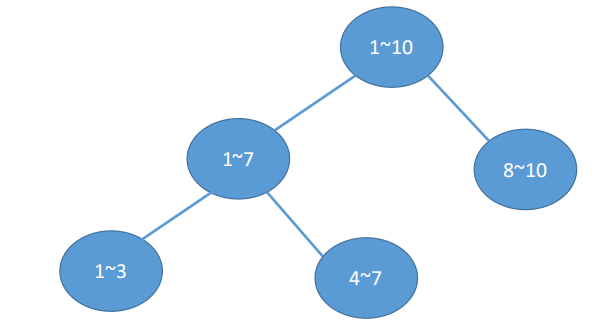
两个核心问题:1.节点切分的依据是什么?
2.如何能进行预测?
根据这两个问题,我们讲解回归树的计算示例:
1、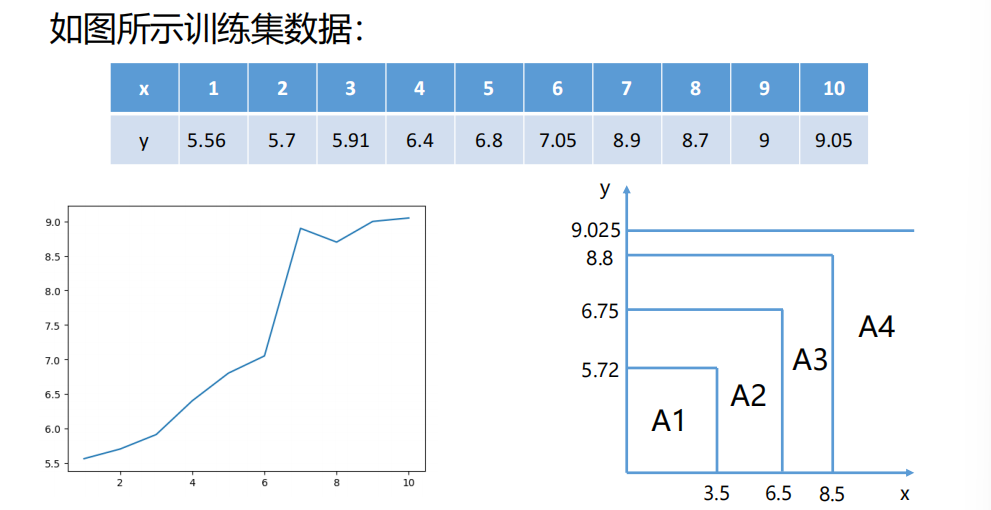
1、计算最优切分点
因为只有一个变量,所以切分变量必然是x,可以考虑如下9个切分点:
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5\]。
【原因:实际上考虑两个变量间任意一个位置为切分点均可】
\<1\>切分点1.5的计算
当s=1.5时,将数据分为两个部分:
第一部分:(1,5.56)
第二部分:(2,5.7)、(3,5.91)、(4,6.4)...(10,9.05)
### 2、计算损失
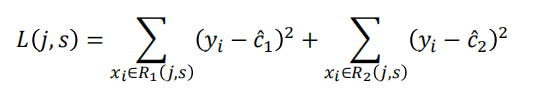
C1=5.56
C2=1/9(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5
Loss = (5.56-5.56)\^2 + (5.7-7.5)\^2+(5.91-7.5)\^2+...+(9.05-7.5)\^2 =0+15.72 =15.72
### 3、同理计算其他分割点的损失
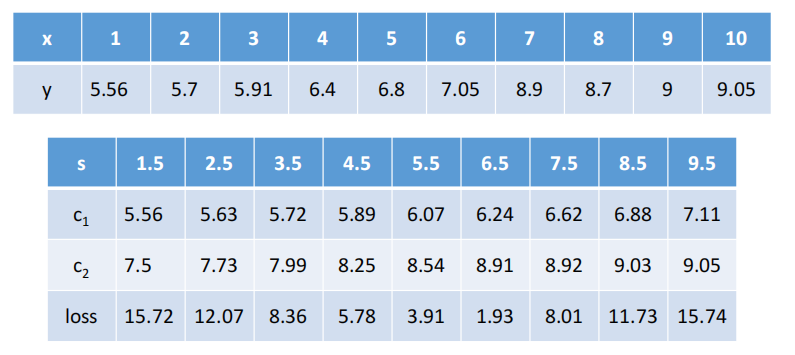
容易看出,当s=6.5时,loss=1.93最小,所以第一个划分点s=6.5。
### 4、对于小于6.5部分

\<1\>切分点1.5的计算
当s=1.5时,将数据分为两个部分:
第一部分:(1,5.56)
第二部分:(2,5.7)、(3,5.91)、(4,6.4)、(5,6.8)、(6,7.05)
Loss = 0 +(5.7-6.37)\^2+(5.91-6.37)\^2 +...+(7.05-6.37)\^2
=0+1.3087=1.3087
C1=5.56
C2=1/5(5.7+5.91+6.4+6.8+7.05)=6.37
### 5、可得出
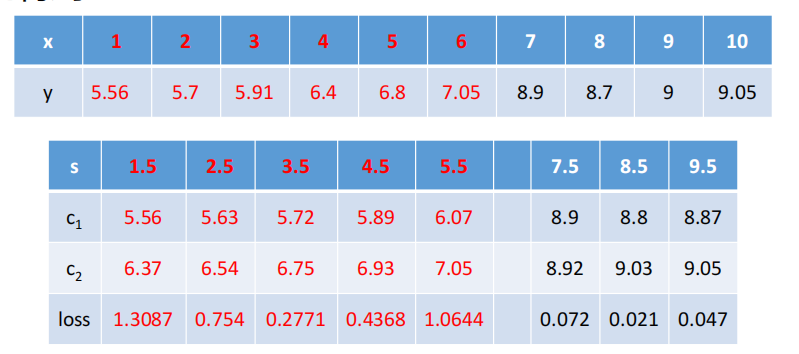
容易看出:\<1\>当s=3.5时,loss=0.2771最小,所以第一个划分点s=3.5。
\<2\>当s=8.5时,loss=0.021最小,所以第二个划分点s=8.5。
### 6、假设只分裂我们计算的这几次

那么分段函数为:
\<1\>当x\<=3.5时,1/3(5.56+5.7+5.91)=5.72
\<2\>当3.5\