各位读者大佬好,我是落羽!一个坚持不断学习进步的学生。
如果您觉得我的文章还不错,欢迎多多三连分享交流,一起学习进步!
欢迎关注我的blog主页: 落羽的落羽
文章目录
- 一、图的遍历
-
- [1. BFS](#1. BFS)
- [2. DFS](#2. DFS)
- [3. 测试](#3. 测试)
- 二、图的最小生成树算法
-
- [1. Kruskal算法](#1. Kruskal算法)
- [2. Prim算法](#2. Prim算法)
一、图的遍历
遍历一个图,针对的是遍历所有顶点 。主要是两种思路:广度优先(BFS)和深度优先(DFS)
上一篇文章讲过了图可以用领接矩阵和领接表存储边,我们以领接矩阵的模版进行讲解
1. BFS
图的广度优先遍历思路是:从起始顶点出发,先访问当前顶点的所有直接邻接顶点(一层),再依次访问这些邻接顶点的邻接节点(下一层),以此类推,直到遍历完所有可达顶点。
曾经我们讲二叉树的广度优先遍历时,是利用了队列结构,这里也是一样的。每次队头元素出队列时,队头元素顶点的所有领接顶点全部入队列。为了防止一个顶点多次遍历,还需要一个数组用于标记。
cpp
// 参数是遍历的起始顶点
void BFS(const V& src)
{
// 得到起始顶点的下标
size_t srcindex = GetVertexIndex(src);
// 防止一个顶点被多次遍历,用一个数组标记被遍历过的下标
vector<bool> visited;
visited.resize(_vertexs.size(), false);
// 起点入队列
queue<int> q;
q.push(srcindex);
visited[srcindex] = true;
cout << "BFS遍历: ";
while (!q.empty())
{
size_t front = q.front();
// 打印出当前遍历顶点
cout << _vertexs[front] << ' ';
// 队头元素出队列
q.pop();
// 队头元素顶点所有没遍历过的相邻顶点入队列,在领接矩阵中查询相邻顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (visited[i] == false && _matrix[front][i] != MAX_W)
{
// 遍历过的顶点标记为true
visited[i] = true;
q.push(i);
}
}
}
// 如果该图不是连通图,这种方法会使某些顶点没遍历到
for (bool check : visited)
{
if (check == false)
{
cout << "该图不是连通图,还有未遍历到的顶点";
}
}
cout << endl;
}2. DFS
图的深度优先遍历核心思想是 "一条路走到黑":从起始顶点出发,沿着一条路径尽可能深地探索,直到无法继续(遇到已访问节点或无邻接顶点),再回溯到上一个顶点,继续探索其他未走的分支。为了防止一个顶点多次遍历,也需要一个数组用于标记。
cpp
void _DFS(size_t srcIndex, vector<bool>& visited)
{
// 当前遍历顶点
cout << _vertexs[srcIndex] << ' ';
visited[srcIndex] = true;
// 找srcIndex的相邻顶点,遍历下去
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (visited[i] == false && _matrix[srcIndex][i] != MAX_W)
{
_DFS(i, visited);
}
}
}
void DFS(const V& src)
{
// 得到起始顶点的下标
size_t srcindex = GetVertexIndex(src);
// 防止一个顶点被多次遍历,用一个数组标记被遍历过的下标
vector<bool> visited;
visited.resize(_vertexs.size(), false);
cout << "DFS遍历: ";
_DFS(srcindex, visited);
cout << endl;
}3. 测试
我们用这张图进行测试:
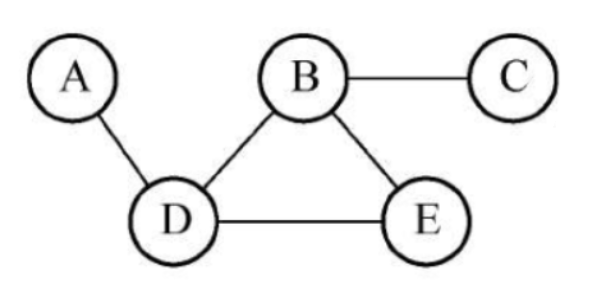
完整代码:
cpp
#pragma once
#include<iostream>
#include<vector>
#include<map>
#include<queue>
using namespace std;
// 邻接矩阵 图
namespace Matrix
{
// V顶点类型 W边权值类型 MAX_W表示边不存在的值 Direction表示图是否有向
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
Graph(const V* vertexs, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(vertexs[i]);
_vIndexMap[vertexs[i]] = i;
}
// MAX_W 作为不存在边的标识值
// 初始化时默认没有边,边需要一条一条手动添加,用AddEdge函数
_matrix.resize(n);
for (auto& e : _matrix)
{
e.resize(n, MAX_W);
}
}
// 找到一个顶点的映射下标
size_t GetVertexIndex(const V& v)
{
auto ret = _vIndexMap.find(v);
if (ret != _vIndexMap.end())
{
return ret->second;
}
else
{
throw invalid_argument("不存在的顶点");
return -1;
}
}
// 添加一条边,src和dst代表两端顶点,w是权值
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_matrix[srci][dsti] = w;
//如果是无向图,则[dsti][srci]也需添加边
if (Direction == false)
{
_matrix[dsti][srci] = w;
}
}
// 参数是遍历的起始顶点
void BFS(const V& src)
{
// 得到起始顶点的下标
size_t srcindex = GetVertexIndex(src);
// 防止一个顶点被多次遍历,用一个数组标记被遍历过的下标
vector<bool> visited;
visited.resize(_vertexs.size(), false);
// 起点入队列
queue<int> q;
q.push(srcindex);
visited[srcindex] = true;
cout << "BFS遍历: ";
while (!q.empty())
{
size_t front = q.front();
// 打印出当前遍历顶点
cout << _vertexs[front] << ' ';
// 队头元素出队列
q.pop();
// 队头元素顶点所有没遍历过的相邻顶点入队列,在领接矩阵中查询相邻顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (visited[i] == false && _matrix[front][i] != MAX_W)
{
// 遍历过的顶点标记为true
visited[i] = true;
q.push(i);
}
}
}
// 如果该图不是连通图,这种方法会使某些顶点没遍历到
for (bool check : visited)
{
if (check == false)
{
cout << "该图不是连通图,还有未遍历到的顶点";
}
}
cout << endl;
}
void _DFS(size_t srcIndex, vector<bool>& visited)
{
// 当前遍历顶点
cout << _vertexs[srcIndex] << ' ';
visited[srcIndex] = true;
// 找srcIndex的相邻顶点,遍历下去
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (visited[i] == false && _matrix[srcIndex][i] != MAX_W)
{
_DFS(i, visited);
}
}
}
void DFS(const V& src)
{
// 得到起始顶点的下标
size_t srcindex = GetVertexIndex(src);
// 防止一个顶点被多次遍历,用一个数组标记被遍历过的下标
vector<bool> visited;
visited.resize(_vertexs.size(), false);
cout << "DFS遍历: ";
_DFS(srcindex, visited);
cout << endl;
}
private:
map<V, size_t> _vIndexMap; // 每个顶点映射一个下标
vector<V> _vertexs; // 顶点集合
vector<vector<W>> _matrix; // 领接矩阵 存储边
};
}
int main()
{
char arr[] = {'C','A','D','B','E'};
Matrix::Graph<char, int> graph(arr, sizeof(arr)/sizeof(char));
// 添加边,权值不用管随便写的
graph.AddEdge('A', 'D', 1);
graph.AddEdge('D', 'B', 2);
graph.AddEdge('D', 'E', 3);
graph.AddEdge('B', 'E', 4);
graph.AddEdge('B', 'C', 5);
graph.BFS('A');
graph.BFS('B');
graph.DFS('A');
graph.DFS('B');
return 0;
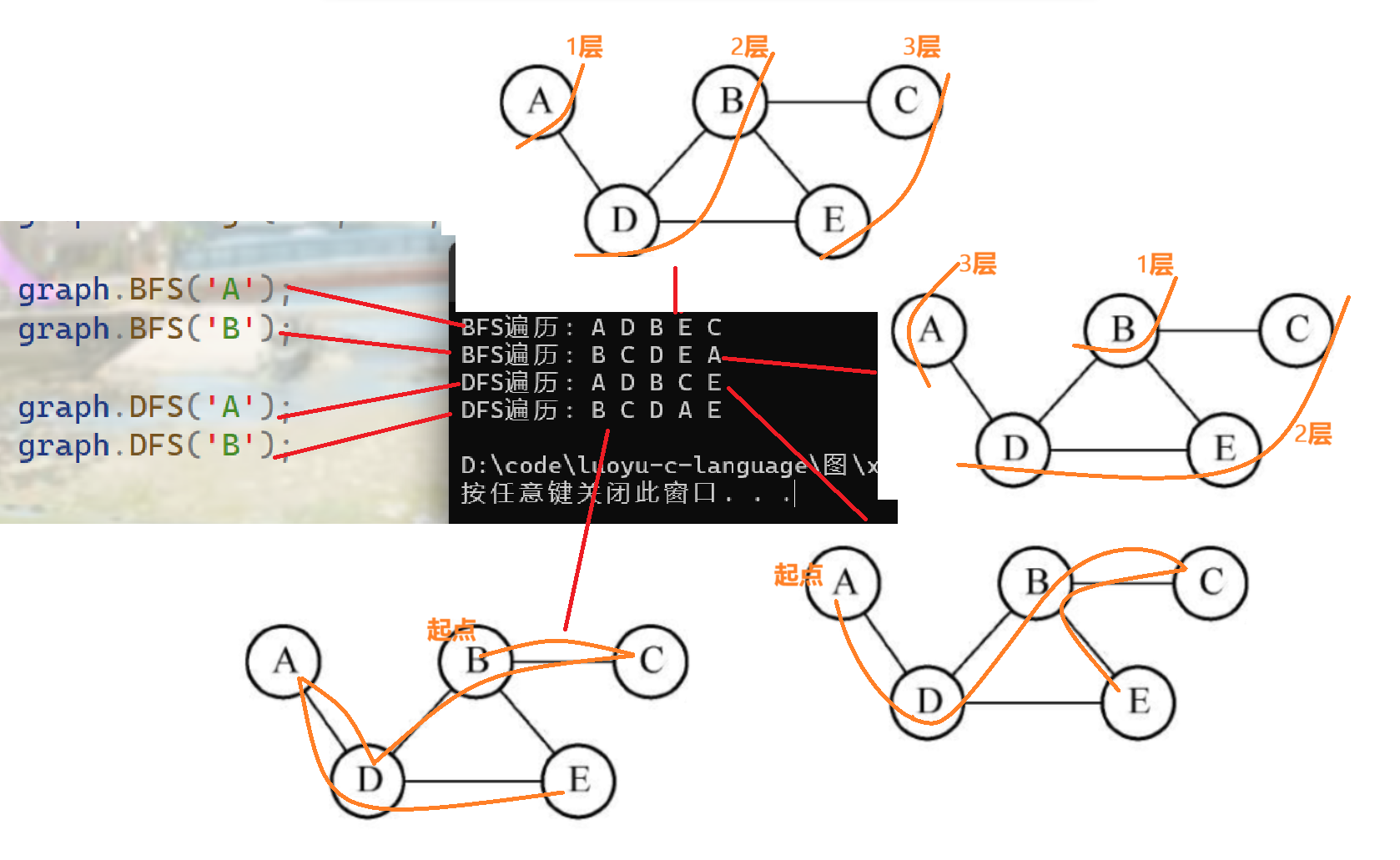
}结果分析,符合BFS与DFS的规则:
二、图的最小生成树算法
连通图的每一棵生成树,都是原图的一个极大无环子图。最小生成树,就是指所有边的权值加起来总权最小的生成树 ,可以理解为用最小的成本构成的生成树。
最小生成树也是生成树,要符合:
- 要包括原图的所有顶点,只能使用原图中的边来构造
- 只能使用恰好n-1条边来连接图中n个顶点
- 选择的n-1条边不能构成回路
- 边的总权值要最小
构造最小生成树一般有两种算法:克鲁斯卡尔(Kruskal)算法、普里姆(Prim)算法,都是用了逐步求解的贪心策略。
1. Kruskal算法
这种算法的思路是"从小到大选边":将所有边按权值从小到大排序,依次选择最小的边,若这条边连接的两个顶点不在同一个已连通集合中,就将这条边加入生成树;否则跳过,避免形成环。重复此过程,直到选够n−1条边。
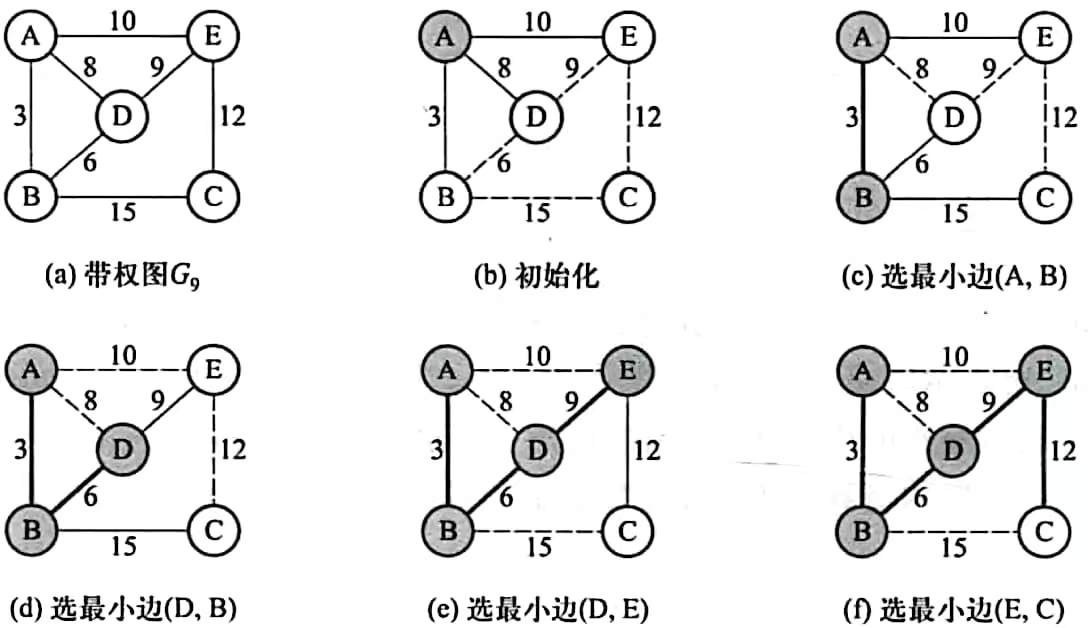
判断两个顶点是否在一个已连通集合,可以利用并查集!详见:并查集的原理与使用
cpp
typedef Graph<V, W, MAX_W, Direction> Self;
struct Edge
{
V _srci;
V _dsti;
W _w;
Edge(const V& srci, const V& dsti, const W& w)
:_srci(srci)
, _dsti(dsti)
, _w(w)
{ }
bool operator<(const Edge& eg) const
{
return _w < eg._w;
}
bool operator>(const Edge& eg) const
{
return _w > eg._w;
}
};
Graph() = default;
// 传递一个图,作为构造最小生成树的结果。返回总权值
W Kruskal(Self& minTree)
{
// 所有顶点拷贝,初始不带任何边
minTree._vertexs = _vertexs;
minTree._vIndexMap = _vIndexMap;
minTree._matrix.resize(_vertexs.size());
for (auto& e : minTree._matrix)
{
e.resize(_vertexs.size(), MAX_W);
}
// priority_queue用于按照权值排序边
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
for (size_t i = 0; i < _matrix.size(); ++i)
{
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
// 无向图,只要判断领接矩阵一半的边
if (i < j && _matrix[i][j] != MAX_W)
{
pq.push(Edge(i, j, _matrix[i][j]));
}
}
}
// 记录总权值
W total = W();
// 贪心算法,从最小的边开始选,将选出的边两端顶点放入一个集合
// size记录已选出边数
int size = 0;
UnionFindSet ufs(_vertexs.size());
while (!pq.empty())
{
Edge min = pq.top();
pq.pop();
// 边两端顶点不在一个集合,说明不会构成环,则添加这条边到最小生成树,两个顶点放到一个集合
if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti))
{
minTree.AddEdge(min._srci, min._dsti, min._w);
total += min._w;
size++;
ufs.Union(min._srci, min._dsti);
}
}
// 若size不等于n-1,说明构建最小生成树失败,返回一个默认值W()
if (size == _vertexs.size() - 1)
{
return total;
}
else
{
return W();
}
}2. Prim算法
Prim算法,是按点贪心:X集合存放已连入生成树的点,Y集合存放未连入生成树的点。一开始所有顶点都在Y中,首先将参数起点放入X并从Y中删除。从X中所有点连出的边中选出"权最小的且有一端顶点在Y中的边",插入到最小生成树中,再把这条边的端点放入X中并从Y中删除。如此循环往复,直到所有顶点都在X中。
这种算法天然避免了环的发生!
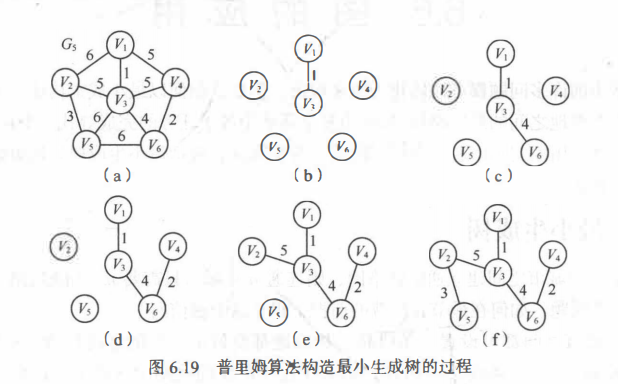
cpp
// 给一个起点
W Prim(Self& minTree, const V& src)
{
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._vIndexMap = _vIndexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
// X和Y集合
vector<bool> X(n, false);
vector<bool> Y(n, true);
X[srci] = true;
Y[srci] = false;
// 从X->Y集合中连接的边里面选出最小的边
priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
// 先把srci连接的边添加到队列中
for (size_t i = 0; i < n; ++i)
{
if (_matrix[srci][i] != MAX_W)
{
minq.push(Edge(srci, i, _matrix[srci][i]));
}
}
size_t size = 0;
W total = W();
while (!minq.empty())
{
Edge min = minq.top();
minq.pop();
if (!X[min._dsti])
{
minTree.AddEdge(min._srci, min._dsti, min._w);
X[min._dsti] = true;
Y[min._dsti] = false;
++size;
total += min._w;
if (size == n - 1)
break;
for (size_t i = 0; i < n; ++i)
{
if (_matrix[min._dsti][i] != MAX_W && Y[i])
{
minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
}
}
}
if (size == n - 1)
{
return total;
}
else
{
return W();
}
}本篇完,感谢阅读
