基于MATLAB实现NSGA-II算法

一、NSGA-II算法核心流程

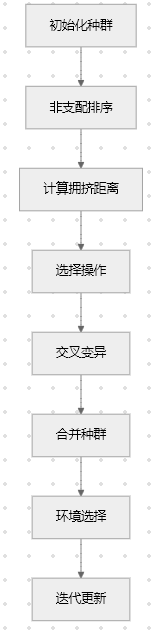
二、MATLAB核心代码实现

1. 参数设置与种群初始化

matlab 复制代码

%% 参数设置
nVar = 3;          % 决策变量维度
VarMin = -5;       % 变量下限
VarMax = 5;        % 变量上限
MaxIt = 100;       % 最大迭代次数
nPop = 100;        % 种群规模
pCrossover = 0.9;  % 交叉概率
pMutation = 0.1;   % 变异概率

2. 非支配排序实现

matlab 复制代码

function fronts = fastNondominatedSort(pop)
    n = numel(pop);
    F = {};
    nDom = zeros(n,1);
    domList = cell(n,1);
    
    % 计算支配关系
    for i = 1:n
        for j = 1:n
            if i ~= j
                if all(pop(i).Obj <= pop(j).Obj) && any(pop(i).Obj < pop(j).Obj)
                    domList{i} = [domList{i}, j];
                elseif all(pop(j).Obj <= pop(i).Obj) && any(pop(j).Obj < pop(i).Obj)
                    nDom(i) = nDom(i) + 1;
                end
            end
        end
        if nDom(i) == 0
            F{1} = [F{1}, i];
        end
    end
    
    % 构建前沿
    i = 1;
    while ~isempty(F{i})
        Q = [];
        for p = F{i}
            for q = domList{p}
                nDom(q) = nDom(q) - 1;
                if nDom(q) == 0
                    Q = [Q, q];
                end
            end
        end
        i = i + 1;
        F{i} = Q;
    end
end

3. 拥挤距离计算

matlab 复制代码

function dist = crowdingDistance(front, obj)
    n = numel(front);
    m = size(obj,2);
    dist = zeros(n,1);
    
    for k = 1:m
        [~, idx] = sort(obj(front,k));
        dist(idx(1)) = Inf;
        dist(idx(end)) = Inf;
        for i = 2:n-1
            dist(idx(i)) = dist(idx(i)) + (obj(front(idx(i+1)),k) - obj(front(idx(i-1)),k));
        end
    end
end

4. 主循环实现

matlab 复制代码

%% 主循环
for it = 1:MaxIt
    % 评估目标函数
    for i = 1:nPop
        pop(i).Obj = ObjectiveFunction(pop(i).Var);
    end
    
    % 非支配排序
    fronts = fastNondominatedSort(pop);
    
    % 拥挤距离计算
    for f = fronts
        idx = f{1};
        pop(idx).Rank = length(fronts) - f{1} + 1;
        pop(idx).Crowding = crowdingDistance(idx, pop.Obj);
    end
    
    % 环境选择
    newPop = [];
    for f = fronts
        if numel(newPop) + numel(f{1}) <= nPop
            newPop = [newPop, pop(f{1})];
        else
            [~, sortIdx] = sort([pop(f{1}).Crowding], 'descend');
            addNum = nPop - numel(newPop);
            newPop = [newPop, pop(f{1})(sortIdx(1:addNum))];
            break;
        end
    end
    
    % 交叉变异
    offspring = [];
    for i = 1:2:numel(newPop)
        parent1 = newPop(randi(numel(newPop)));
        parent2 = newPop(randi(numel(newPop)));
        child1 = crossover(parent1.Var, VarMin, VarMax);
        child2 = mutation(child1.Var, VarMin, VarMax);
        offspring = [offspring, struct('Var',child1), struct('Var',child2)];
    end
    
    % 合并种群
    pop = [newPop, offspring];
end

三、关键参数优化

参数	推荐范围	优化建议
种群规模(nPop)	50-200	目标维度每增加1维，增加20%
交叉概率(pC)	0.7-0.9	高维问题建议0.85
变异概率(pM)	0.05-0.15	复杂问题可增至0.2
迭代次数(MaxIt)	100-500	收敛曲线监控调整

四、典型应用案例

1. 多目标工程设计优化

matlab 复制代码

% 目标函数：最小化成本和最大化强度
f1 = @(x) sum(x.^2);          % 成本函数
f2 = @(x) -prod(x+1);         % 强度函数（取负求最小）

% 定义优化问题
problem = struct(...
    'Objective', {@f1, @f2}, ...
    'VarMin', [0,0], ...
    'VarMax', [10,10], ...
    'nObj', 2);

% 运行NSGA-II
options = optimoptions('gamultiobj',...
    'PopulationSize', 100,...
    'CrossoverFcn', @simulatedBinaryCrossover,...
    'MutationFcn', @polynomialMutation);
[x, fval] = gamultiobj(problem.Objective, 2, [], [], [], [], ...
    problem.VarMin, problem.VarMax, [], options);

2. 电力系统多目标调度

matlab 复制代码

% 目标函数：最小化运行成本和排放量
CostFunction = @(x) [sum(x.*CostMatrix), sum(x.*EmissionMatrix)];

% 约束条件
A = [1,1; 2,1];  % 线性约束矩阵
b = [100; 80];   % 线性约束右侧

% 调用gamultiobj
[x,fval] = gamultiobj(CostFunction, 2, A, b, [], [], [0,0], [100,100]);

五、可视化分析

matlab 复制代码

%% 帕累托前沿绘制
figure;
plot(fval(:,1), fval(:,2), 'bo');
xlabel('Objective 1');
ylabel('Objective 2');
title('Pareto Front');
grid on;

%% 目标空间分布
figure;
scatter3(fval(:,1), fval(:,2), fval(:,3));
xlabel('Cost'); ylabel('Strength'); zlabel('Efficiency');
title('Multi-Objective Space');

参考代码基于matlab的NSGA-II算法 www.youwenfan.com/contentcso/96073.html

六、常见问题解决方案

早熟收敛 增加变异概率（建议0.1-0.2）采用NSGA-III的参考点机制
计算效率低 使用SIMD指令优化目标函数采用近似模型（如RBF代理模型）
高维问题处理 降维技术（PCA/T-SNE）分解方法（MOEA/D）

七、扩展应用场景

工程设计优化 机械结构参数优化电路设计多目标求解
经济调度 电力系统运行优化供应链库存管理
机器学习 超参数自动调优模型架构搜索