【北邮-研-图论】网络最大流的标号算法V1.0

青山如墨雨如画2025-12-22 11:49

目录

一、准备和声明

1.1、本工程采用C++17标准

1.2、本报告中专有名词解释

1.3、工程初衷和免责声明

二、网络流问题综述

2.1、网络流问题定义

2.2、网络最大流定义

2.3、网络最大流重要性

2.4、网络流数学建模

2.5、标号算法综述

原图及所有存储元素

2.6、标号算法流程图

step1：广度搜索算法寻找增广链

step2：修改增广链上的当前弧流量

[step3： 广度搜索算法寻找增广链​编辑](#step3： 广度搜索算法寻找增广链编辑)

step4：修改增广链上当前弧流量

[step5： 广度搜索算法寻找增广链](#step5： 广度搜索算法寻找增广链)

三、弧参量定义检查模块

3.1、存储结构

3.2、数组赋值函数

3.2.1、存在原因

3.2.2、函数主体

3.2.3、赋值过程

3.2.4、简便写法

3.2.5、效果

四、节点标号模块

4.1、综述

4.2、流程演示

4.3、存储结构

4.4、打印节点信息

4.5、节点信息初始化

4.6、标号模块

step1：网络发点的处理

step2：选取入队节点的条件

[step3： 最大增加流量的分类赋值](#step3： 最大增加流量的分类赋值)

step4：弹出队列节点的处理

step5：标号结束后判断是否存在增广链

标号过程完整代码

五、调整模块

六、最大流标号算法模块

七、整体代码

7.1、head.h【头文件】

7.2、edge.h【弧参量定义模块.h】

7.3、node.h【标号调整模块.h】

7.4、edge.cpp【弧参量定义模块.cpp】

7.5、node.cpp【标号调整模块.cpp】

7.6、source.cpp【源文件】

八、运行结果

一、准备和声明

1.1、本工程采用C++17标准

（1） C++14标准的缺点：

工程是多文件系统，在定义并赋值全局变量时，C++14旧标准需要先在头文件中使用extern声明全局变量，并在使用该全局变量的头文件和源文件中赋值。这种先声明后赋值的方式，对于本工程中对于网络的【弧】的存储格式【结构体二维数组】、以及【节点】的存储格式【结构体一维数组】这两个全局变量很不友好，因为有很多工程文件要调用这两个全局变量，所以每有一个源文件使用一次，就需要在该文件中重新赋值一次，这就导致：存储空间过大、代码重复太多；

（2）C++17标准的优点：

C++17标准在解决本问题中体现了优越性。C++17中，在头文件中定义全局变量和给全局变量赋值可以【同时进行】，只需要在变量的数据结构之前加关键词【inline】。

1.2、本报告中专有名词解释

【弧起点】和【弧终点】分别代表某弧的起止点；

【网络发点】和【网络收点】分别代表整个网络流图的起止点

1.3、工程初衷和免责声明

本工程性质为兴趣导向、自主练习，因大三下学期参加研究生课程《图论及其应用》，对其中"网络最大流问题"很感兴趣，故通过研究教材及某站视频，自行实现，如有雷同，实属抬举本人；

本工程为v1.0版，可能存在算法时空复杂度高、代码书写冗余、对接用户实现交互功能时考虑不周、异常检测排除情况不够全面等问题；如发现问题，欢迎诸前辈莅临斧正，本人会在后续【日志】或【博客】中修改更新；

待补充。

二、网络流问题综述

2.1、网络流问题定义

网络流问题描述的是这样一类场景：在一个由若干节点和连接这些节点的有向线路组成的系统中，存在一处称为起点的节点，一处称为终点的节点，以及若干中间节点。每条线路都具备允许通过的最大通行能力。

问题的核心是，在不使任何一条线路超出其通行能力，并且保证每个中间节点"进来多少就出去多少"的前提下，探讨从起点到终点的可行通行方案。

2.2、网络最大流定义

网络最大流是指在满足上述所有通行能力限制和节点平衡规则的所有可行通行方案中，能够从起点出发并最终到达终点的【最大通行量】。它代表了该系统在不破坏任何线路承载极限的情况下，能够实现的【最高输送效率】。

2.3、网络最大流重要性

明确网络最大流，相当于为各类实际网络系统找到了一条"能力上限"的标杆。无论是在【城市道路规划】、【通信带宽配置】，还是【紧急资源调度】中，掌握这一上限都能帮助决策者判断现有设施是否足够、瓶颈位于何处，以及新增投入是否值得，从而避免盲目扩建或资源浪费。

2.4、网络流数学建模

（max_stream，available_stream）<==>（弧容量，当前弧流量）

如果问题中没有给出当前弧流量，默认为0。

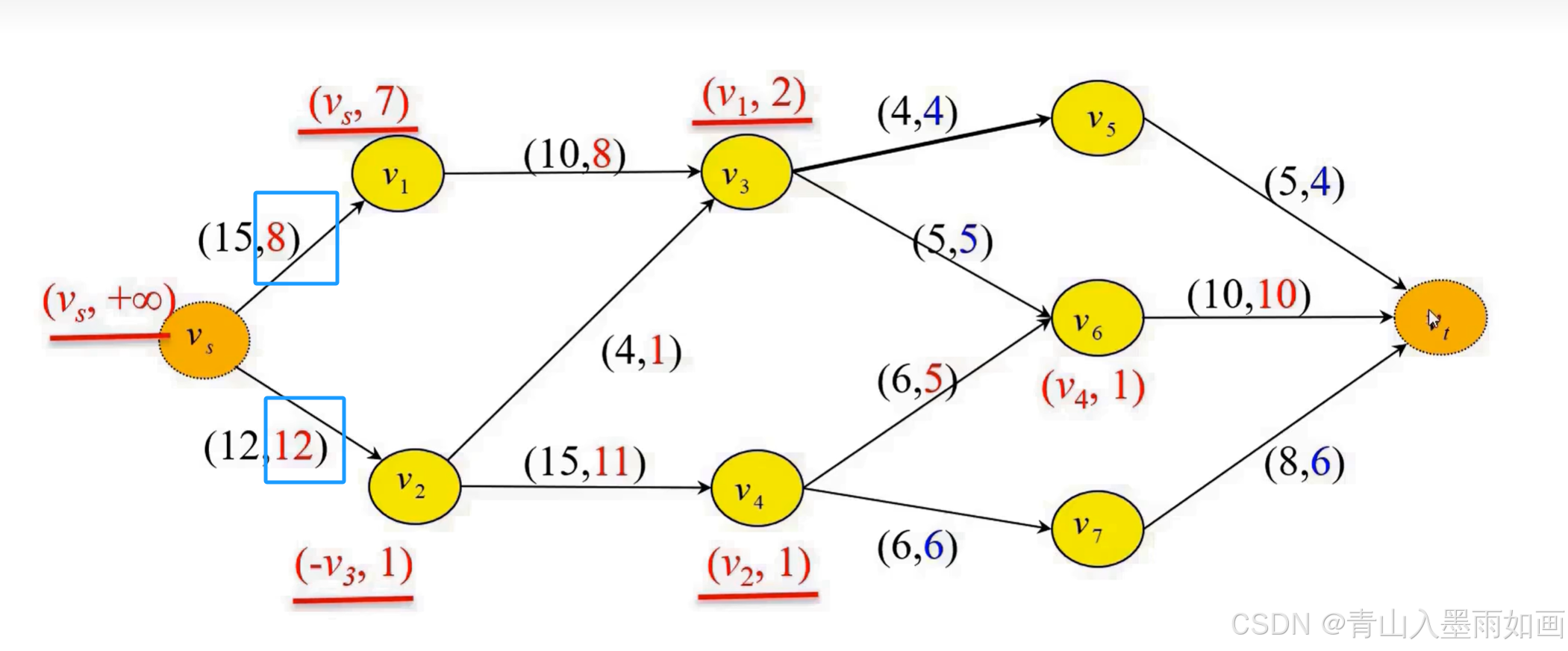
2.5、标号算法综述

求解网络最大流问题，标号算法的视线途径是先找到增广链，之后修改增广链上的当前弧流量，直到无法找到增广链为止，当前网络可行流即为该网络的最大流。

寻找增广链的过程是一个【广搜】过程，BFS算法，那么很容易联想到【队列】；每次从队头弹出一个节点，都从队尾压入【可到达的】、【符合条件的】节点，为节点信息赋值标号；若队头节点是网络收点说明找到了增广链，否则没有增广链；

调整网络可行流的过程：从网络收点开始，依据该节点的源节点依次溯回，直到网络发点；每次溯回，分正反向弧两种情况对应调整该弧可行流；溯回到发点后，格式化所有节点的信息；

重复寻找增广链过程+调整网络可行流过程，直到无法找到增广链，则当前网络可行流就是网络最大可行流。

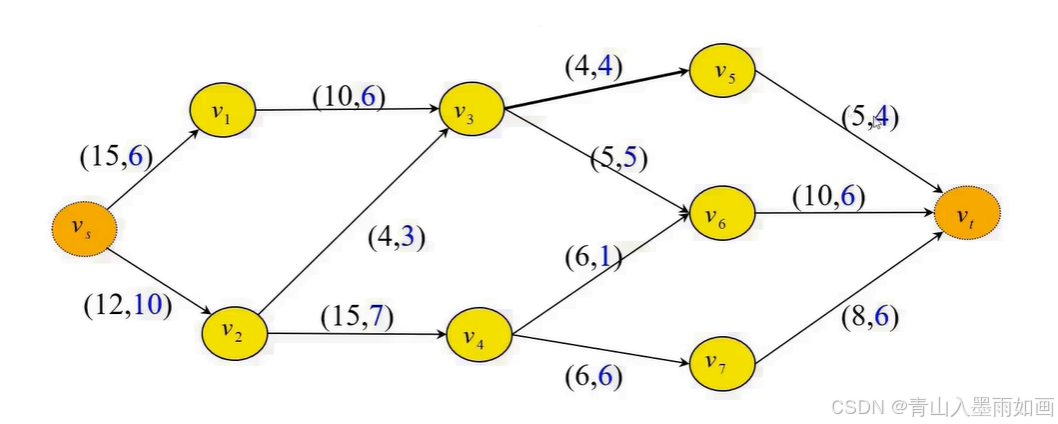
原图及所有存储元素

2.6、标号算法流程图

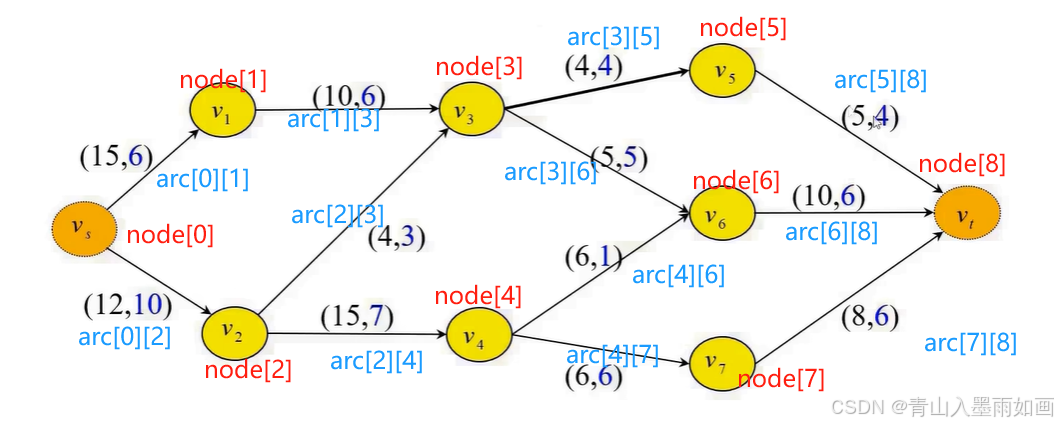
step1：广度搜索算法寻找增广链

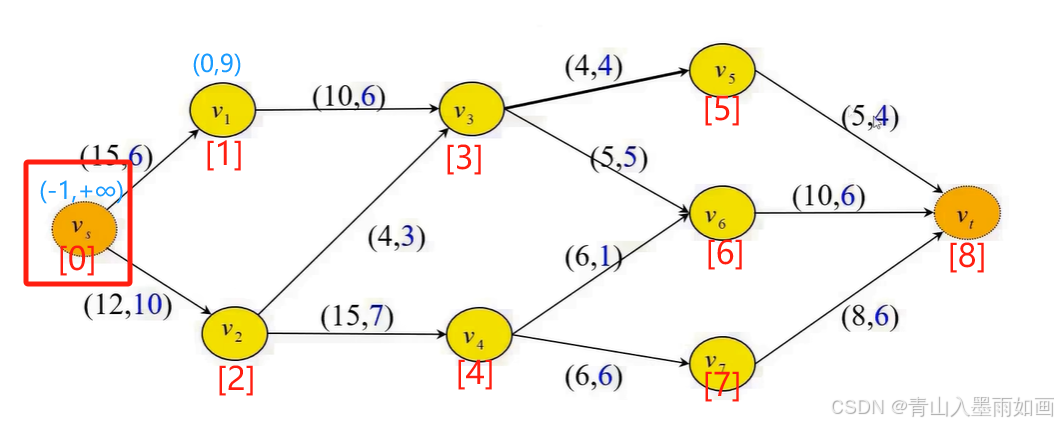
node[0]入队：

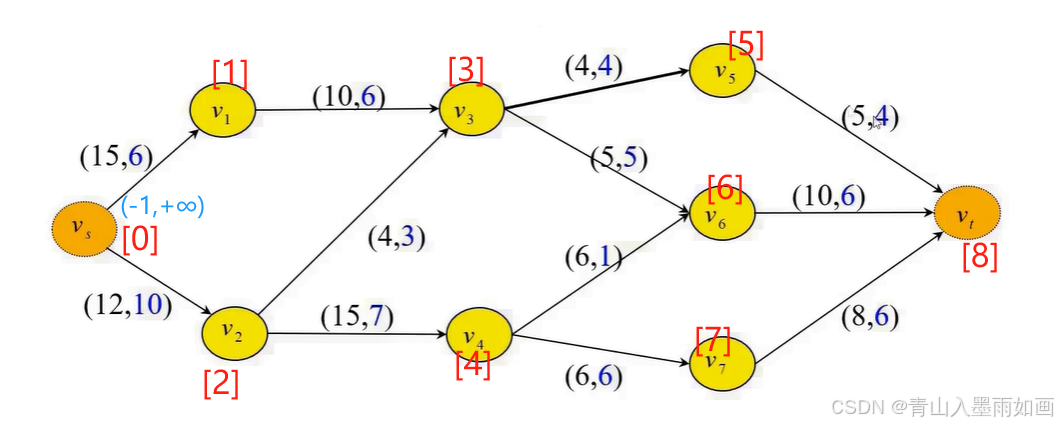
node[0] 出队，node[1]和node[2]入队；

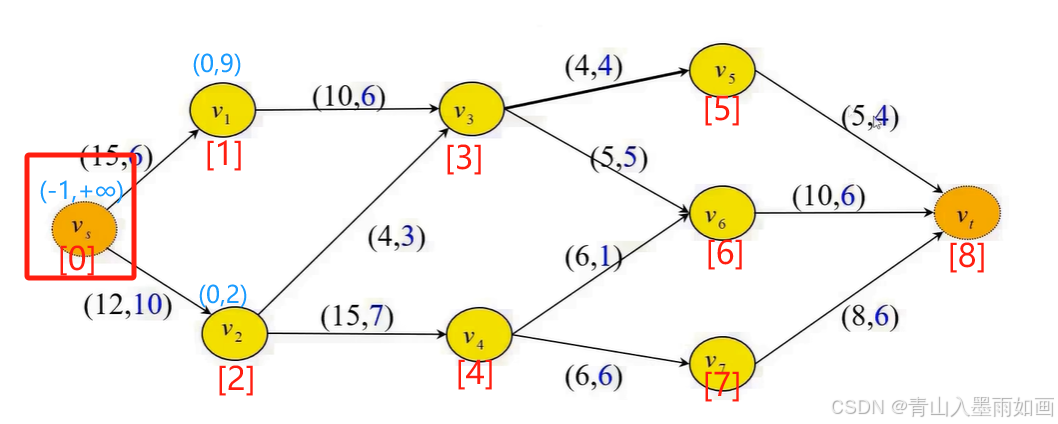
node[1]出队，node[3]入队：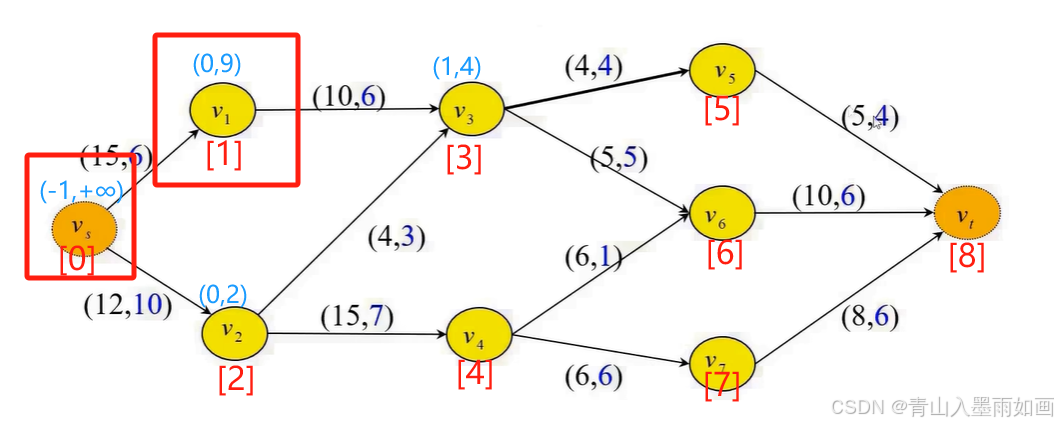

node[2]出队，node[4]入队：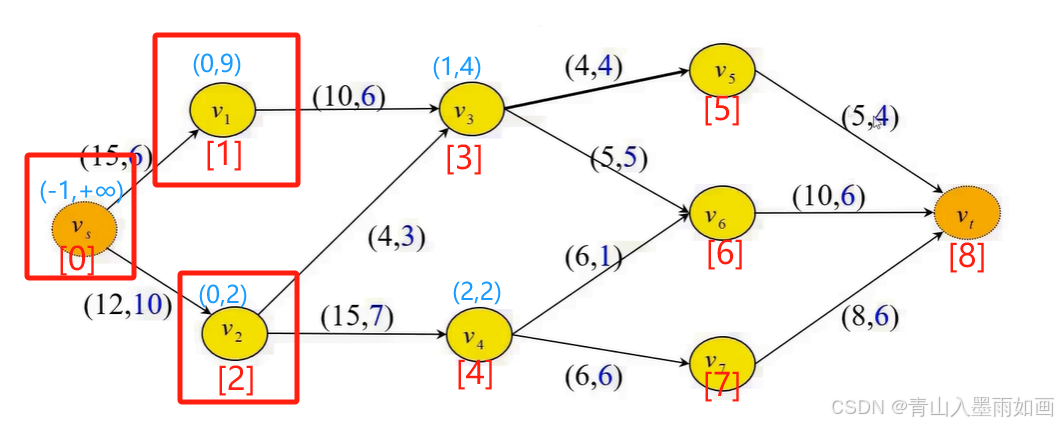

node[3]出队，node[5]、node[6]无法入队：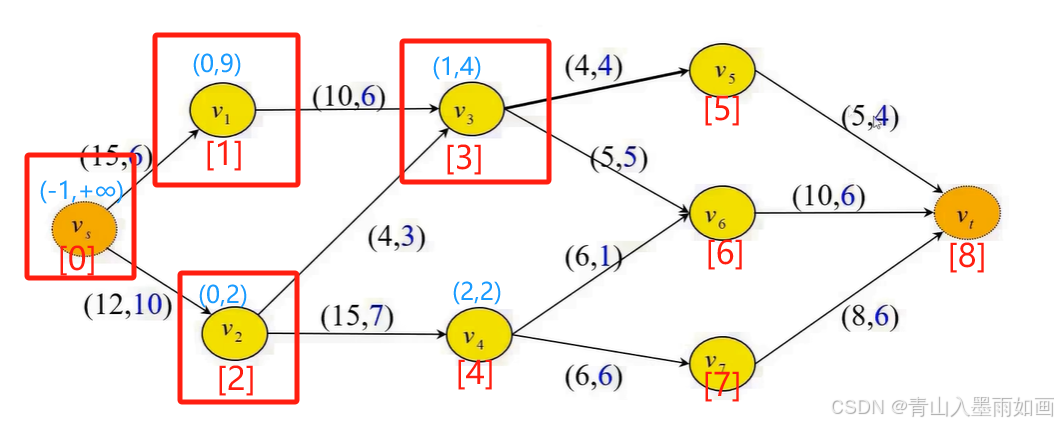

node[4]出队，node[6]入队，[7]无法入队：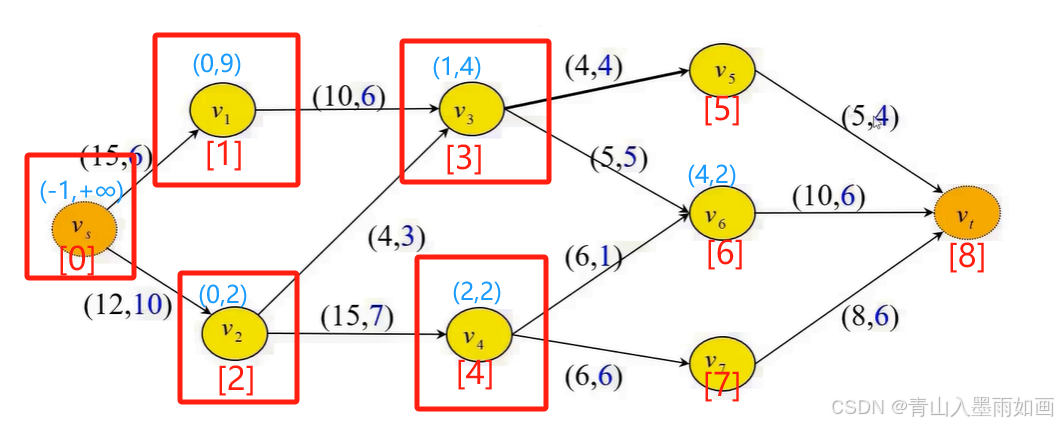

node[6]出队，node[8]入队：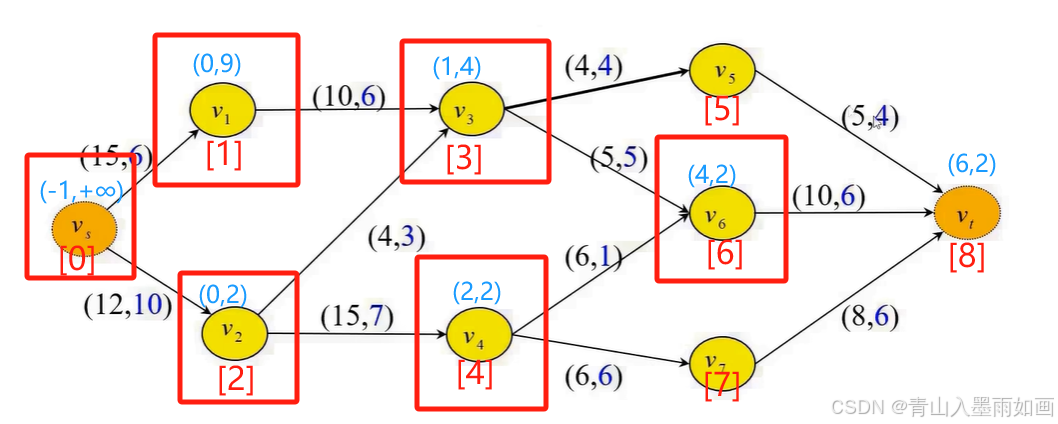

node[8]出队：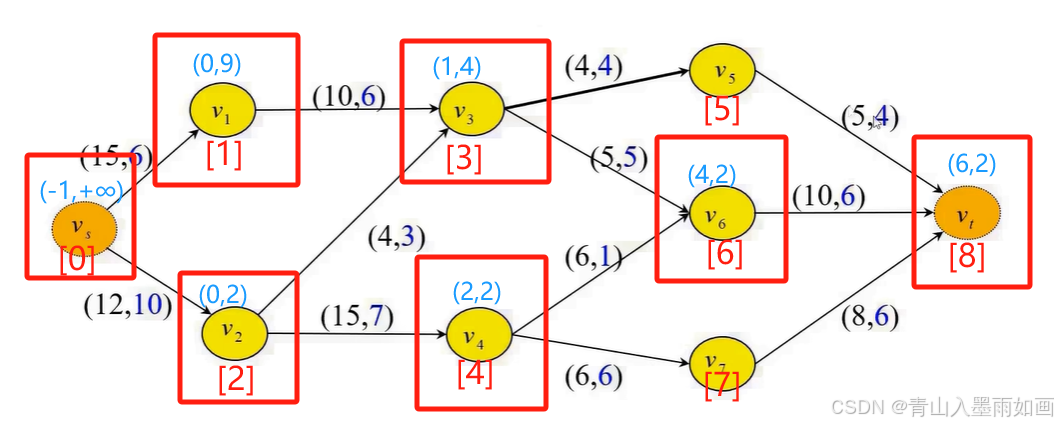

从node[max_node]。source_node回溯，依次是：node[8]::(6,2)->node[6]::(4,2)->node[4]::(2,2)->node[2]::(0,2)->node[0]::(-1,+∞)，因此可以确定增广链：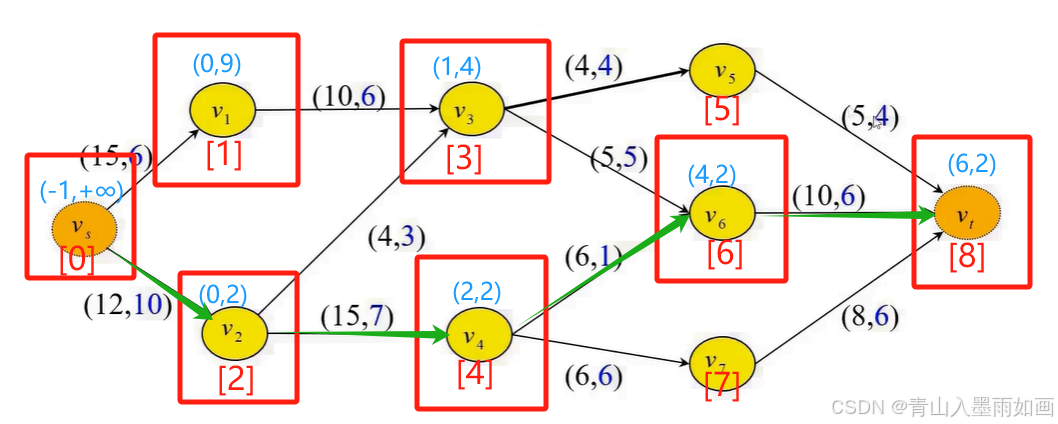

step2：修改增广链上的当前弧流量

因上图得出的增广链所有流方向都是正向，所以每条弧上的当前弧容量+2；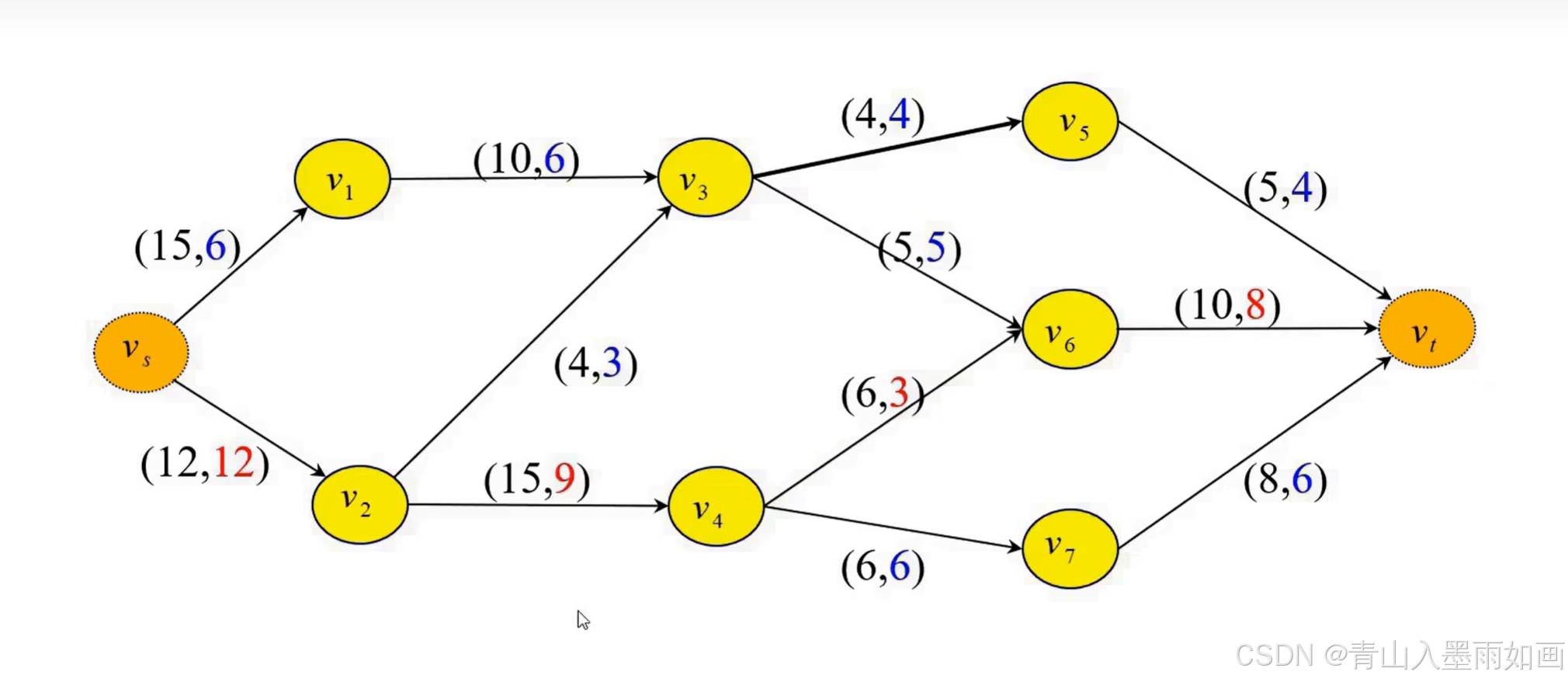

step3： 广度搜索算法寻找增广链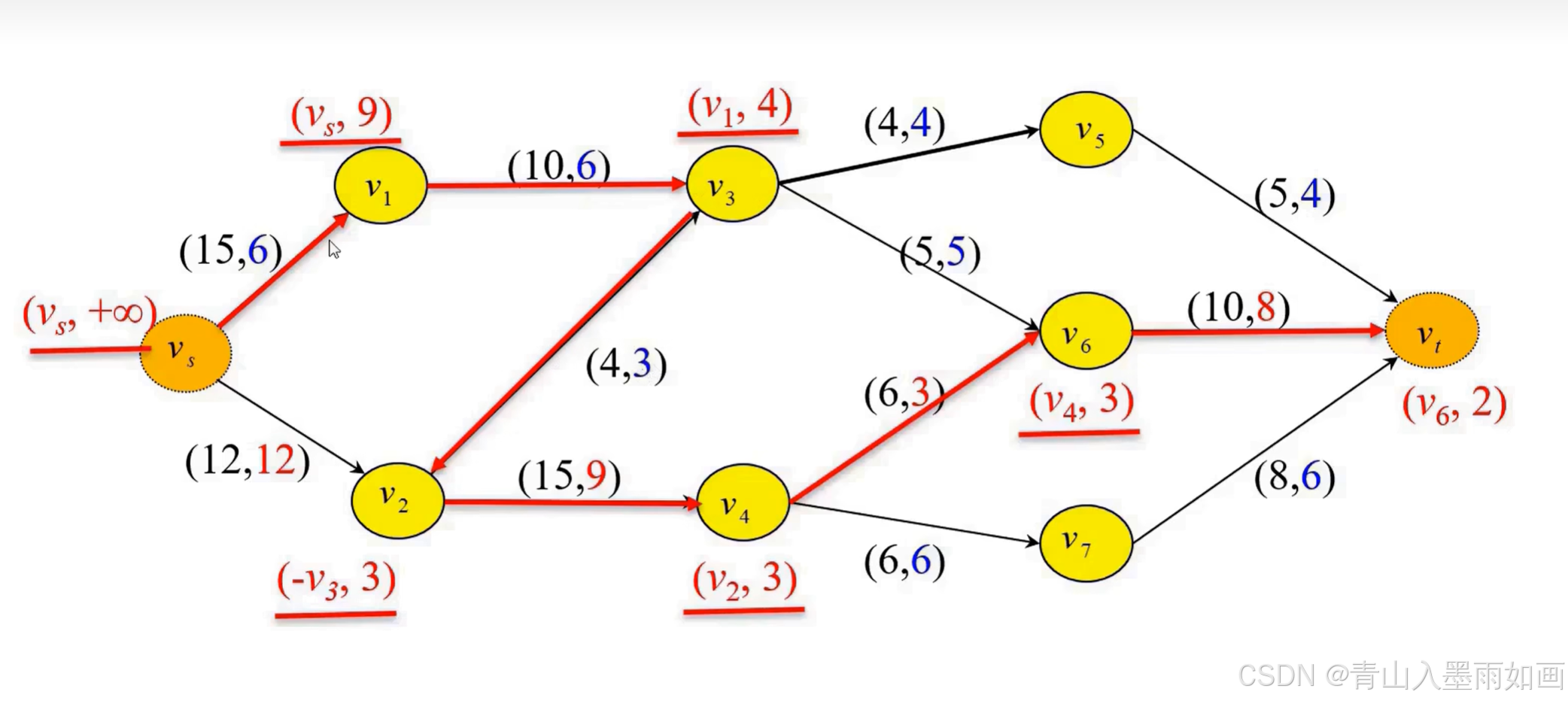

step4：修改增广链上当前弧流量

可以发现，有一条弧是反向流，对于反向流，相应弧上的当前弧流量应该减去对应值2。

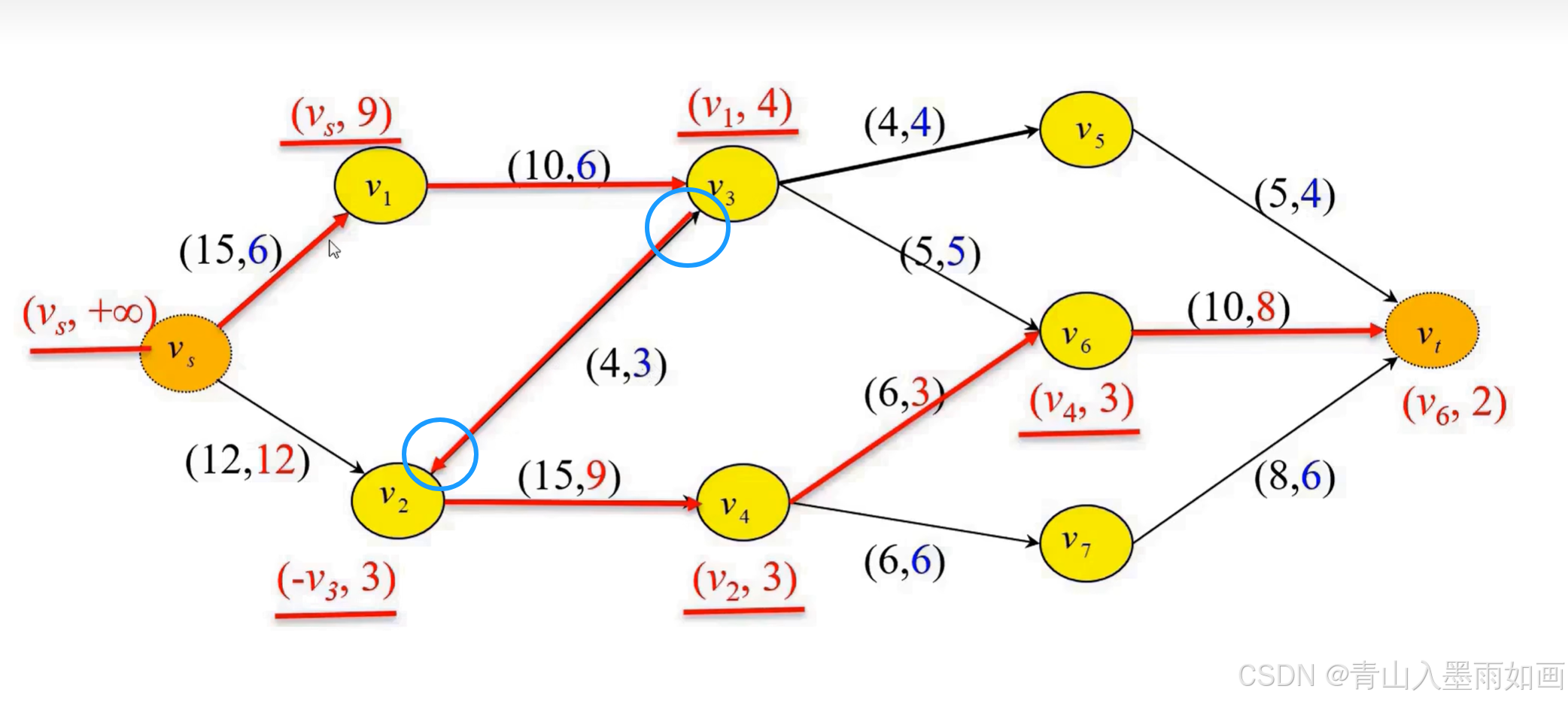
修改后：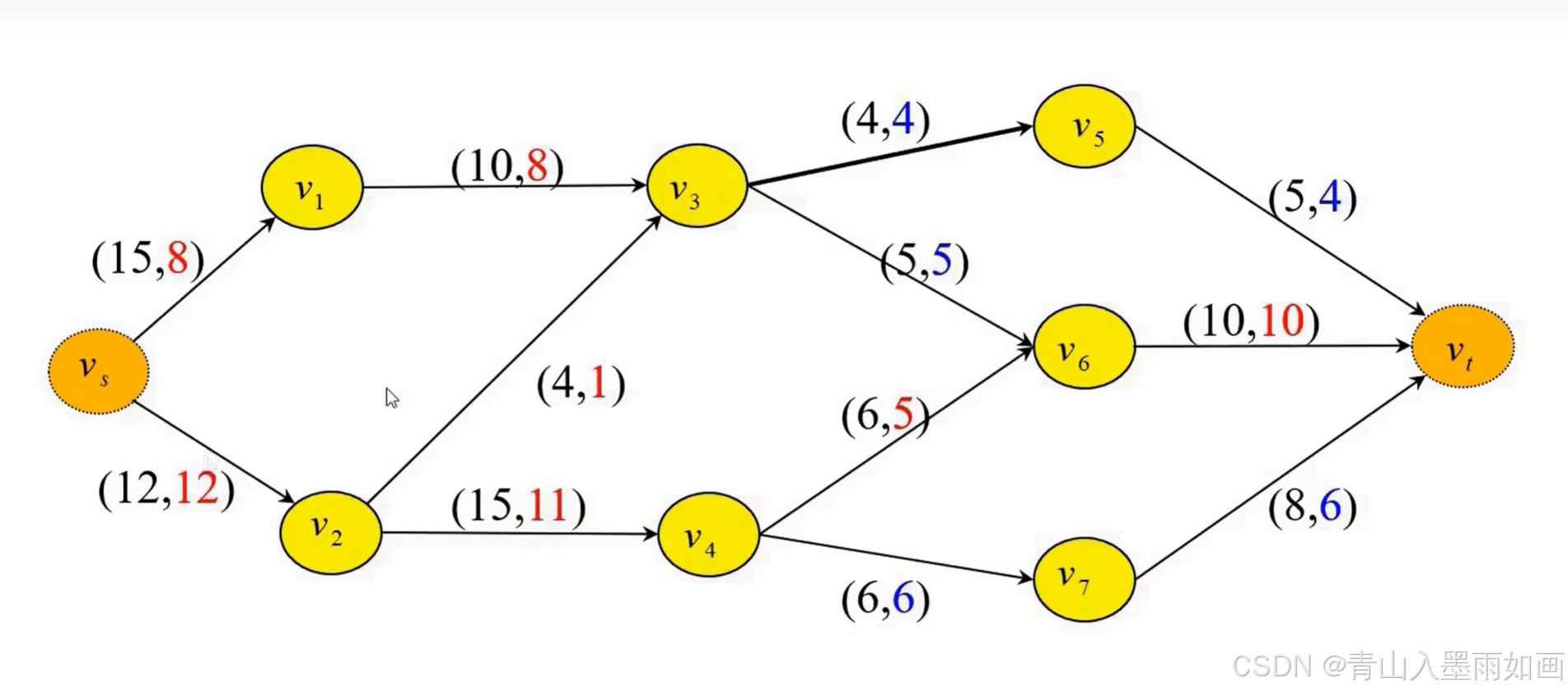

step5： 广度搜索算法寻找增广链

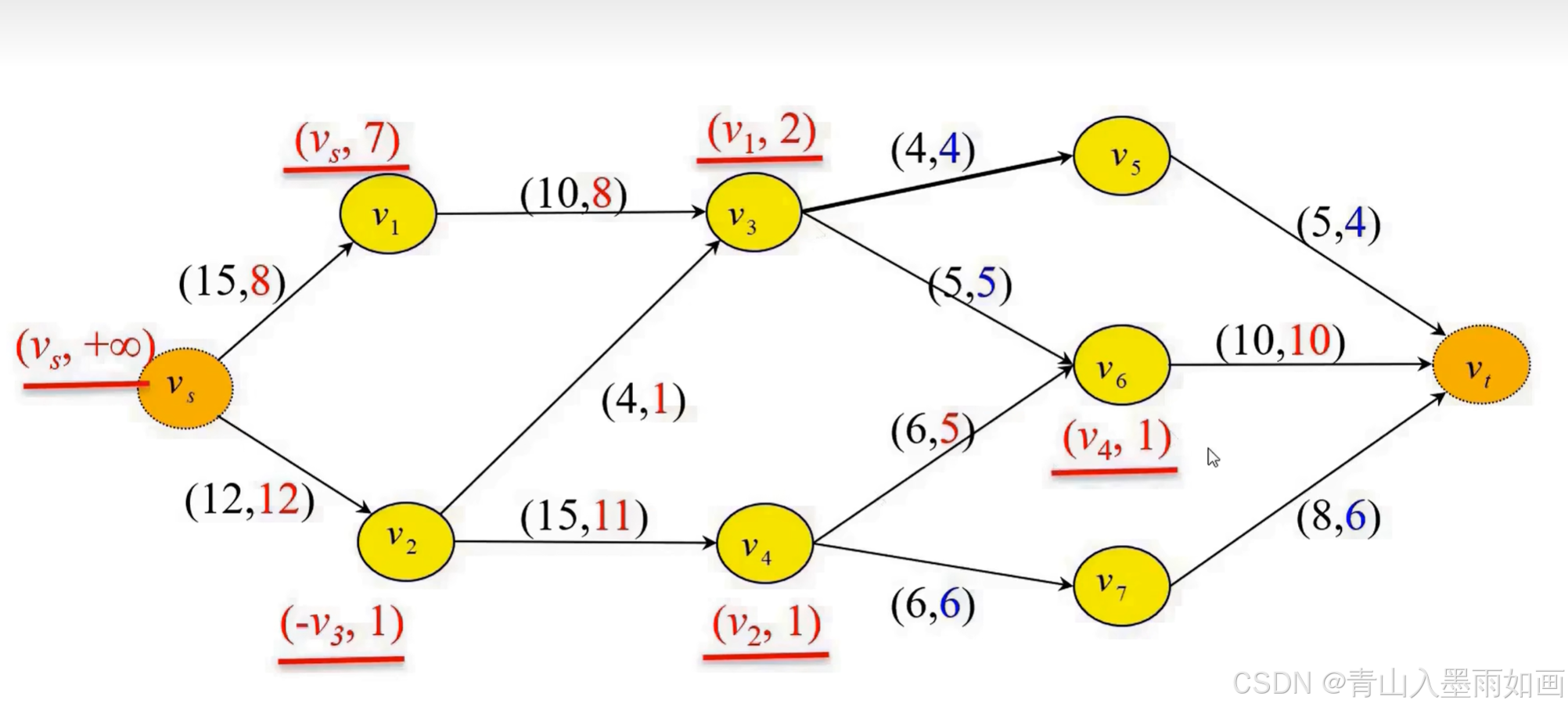
发现网络收点没有被标号到，说明现在已经找不到增广链了，说明现在的可行流就是最大流。

三、弧参量定义检查模块

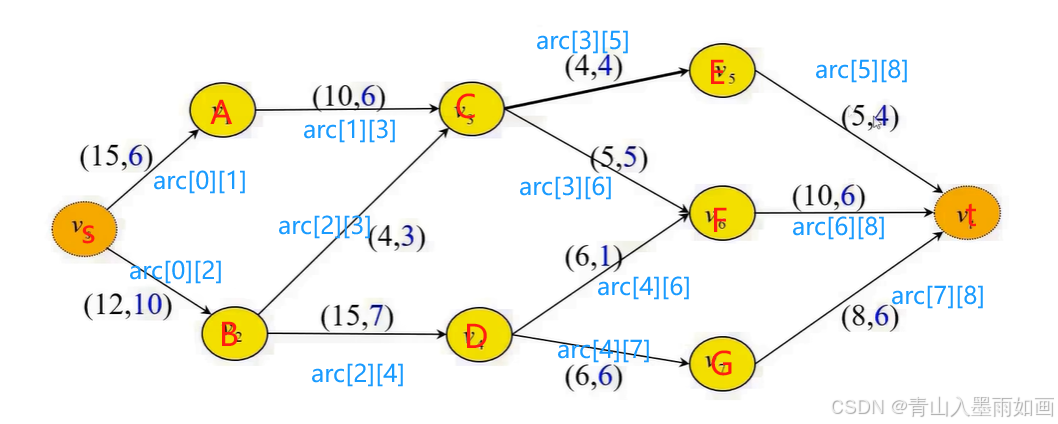
3.1、存储结构

（1）弧容量max_stream；

（2）当前弧流量available_stream；

（3）手动赋值标志initialize_flag；

cpp 复制代码 
const int max_node = 9;
const double INF = 1e5;
struct edge
{
	double max_stream;
	double available_stream;
	bool initialize_flag;
	edge& operator = (edge& a)
	{
		if (this != &a)
		{
			initialize_flag = a.initialize_flag;
			max_stream = a.max_stream;
			available_stream = a.available_stream;
		}
		return *this;
	}
	friend ostream& operator <<(ostream& output, const edge& a)
	{
		output << setiosflags(ios::left);
		output << "{";
		if (a.max_stream == INF)output << "INF";
		else output << setw(3) << a.max_stream;
		output << "," << setw(3) << a.available_stream << "},";
		return output;
	}
};
inline edge arc[max_node][max_node] =
{
	{{INF,0  },{15 ,6  },{12 ,10 },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{10 ,6  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{4  ,3  },{15 ,7  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{4  ,4  },{5  ,5  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{6  ,1  },{6  ,6  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{5  ,4  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{10 ,6  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{8  ,6  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }}
};

//inline edge arc[max_node][max_node];

3.2、数组赋值函数

3.2.1、存在原因

矩阵是稀疏矩阵，录入完整矩阵工作量太大，为了减少工作量，只需录入所有存在弧容量的一步通路即可。

比如示例中给出的矩阵，只需手动录入：

始发节点 终到节点 弧容量 弧流量
s A 15
s B 10
A C 10
B C 4
B D 15
C E 4
C F 5
D F 6
D G 6
E t 5
F t 10
G t 8
[手动录入]
cpp 复制代码 
const int max_node = 9;
const double INF = 1e5;
edge arc[max_node][max_node];

void edge_initialize(bool state)
{
	char start_node = 0, end_node = 0;            //始发节点、终到节点
	double max_stream = 0, available_stream = 0;  //弧容量、当前弧流量
	bool initialize_flag = 1, correct_flag = 1;   //手动输入赋值标志、用户判断输入正确标志
	cout << "数组初始化开始......" << endl;
	cout << "请按照提示输入对应数据......" << endl;
	cout << "注意：若要终止数组初始化，在"始发节点"处输入字符'0'即可。" << endl;
	cout << "注意：网络图起始点用's',终止点用't'。" << endl;
	cout << "注意：若输入错误，只需将弧容量赋值为0，并重新输入该条一步通路即可。" << endl;
	while (1)
	{
		cout << "请输入始发节点(大写字母):"; cin >> start_node;
		if (start_node == '0'){cout << "输入结束!" << endl; break;}
		cout << "请输入终到节点(大写字母):"; cin >> end_node;
		cout << "请输入弧容量:"; cin >> max_stream;
        //......
		if (state == 1)
		{
			cout << "请输入当前弧流量:"; cin >> available_stream;
            //......
		}
        //......
	}
    //......
}

3.2.2、函数主体

首先应该建立死循环，当执行到某条件时判定为输入结束，则循环结束；

输入始发节点（start_node）、终到节点（end_node）、弧容量（max_stream）；如果问题中有考虑当前弧流量（available_stream），则应同时输入当前弧流量；

可见，不妨设置：当始发节点输入为字符'0'时，循环终止；

不妨设置：问题中考虑当前弧流量则给函数传参1，否则传参0；

由于用户不懂节点名称和数组下标对应关系，所以用户输入应为各大写字母节点名，网络发点和网络收点分别用【小写字母's'】和【小写字母't'】来表示；

此处应【考虑用户手误】，即【可以自行发现和修改的错误】------可以设置：若用户发现某流输入错误，则只需令该流的弧容量为0，即可重新输入该流；

用户输入无误后，给全局变量的二维数组【循环赋值】；

手动输入全部赋值过后，对二维数组其他未手动输入赋值的，网络弧容量赋值无穷大（数学意义上的无穷大，编程上可以宏定义一个比所有弧容量都大的数INF）；

由此可见，因为要循环寻找未经手动输入赋值的数组元素，所以对前面每一次手动赋值的元素都给一个赋过值的标记（比如定义一个bool类型的结构体成员initialize_flag），这样现在只需寻找没有该标记的数组元素即可（initialize_flag == 0）；

cpp 复制代码 
const int max_node = 9;
const double INF = 1e5;
edge arc[max_node][max_node];

void edge_initialize(bool state)
{
	char start_node = 0, end_node = 0;
	double max_stream = 0, available_stream = 0;
	bool initialize_flag = 1, correct_flag = 1;
	cout << "数组初始化开始......" << endl;
	cout << "请按照提示输入对应数据......" << endl;
	cout << "注意：若要终止数组初始化，在"始发节点"处输入字符'0'即可。" << endl;
	cout << "注意：网络图起始点用's',终止点用't'。" << endl;
	cout << "注意：若输入错误，只需将弧容量赋值为0，并重新输入该条一步通路即可。" << endl;
	while (1)
	{
		cout << "请输入始发节点(大写字母):"; cin >> start_node;
		if (start_node == '0'){cout << "输入结束!" << endl; break;}
		cout << "请输入终到节点(大写字母):"; cin >> end_node;
		cout << "请输入弧容量:"; cin >> max_stream;
		correct_flag = 1;//不然第一次输入错了，第二次输入correct_flag还是0，没法录值
		if (max_stream == 0)correct_flag = 0;
		if (state == 1)
		{
			cout << "请输入当前弧流量:"; cin >> available_stream;
			if(correct_flag)
				//......
                //此处为二维数组元素的结构体成员available_stream赋值
		}
		if (correct_flag)
		{
            //......
            //......
            //此处为二维数组元素的结构体成员max_stream和initialize_flag赋值
		}
	}
	//未被认为赋值的，initialize_flag = 0，弧容量无穷大；
	for (int i = 0; i < max_node; i++)
		for (int j = 0; j < max_node; j++)
			if (arc[i][j].initialize_flag == 0)
				arc[i][j].max_stream = INF;
}

3.2.3、赋值过程

对全局变量赋值的过程，因用户输入有大小写字母，因此赋值时存在诸多比较判断过程：

对二维结构体数组的某元素的某成员赋值时，应判断：

{

若弧起点（start_node）和弧终点（end_node）均不是网络发点（'s'）和网络收点（'t'），则应为arc[start_node - 'A' + 1][end_node - 'A' + 1]结构体中的成员赋值；

若弧起点是网络发点（即start_node == 's'），则应为arc[ 's' - 's' ][end_node - 'A' + 1]，即arc[0][end_node - 'A' + 1]结构体中的成员赋值；

若弧终点是网络收点（即end_node == 't'），则应为arc[start_node - 'A' + 1][max_node - 1]结构体中的成员赋值；

}

对二维结构体数组的某元素复制时，应判断到底赋值哪些成员：

{

若实际问题中未考虑当前弧流量，则不用给arc[ ][ ].available_stream赋值，否则给其赋值；

因arc[ ][ ]是全局变量，所以有所有元素都有表示0或无的初值；

给arc[ ][ ].max_stream赋值；

给arc[ ][ ].initialize_flag赋值；

}

3.2.4、简便写法

综上，可以看出，赋值首先要考虑"给哪个数组元素赋值"，又要考虑"给哪个成员赋值"，如果一一写出，函数应该特别繁琐：

cpp 复制代码 
void input_switch_available_stream(char start_node, char end_node, double available_stream)
{
	if (start_node == 's' || end_node == 't')
	{
		if (start_node == 's')
			arc[0][end_node - 'A' + 1].available_stream = available_stream; 
		if (end_node == 't')
			arc[start_node - 'A' + 1][max_node - 1].available_stream = available_stream;
	}
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].available_stream = available_stream;
}

void input_switch_max_stream(char start_node, char end_node, double max_stream)
{
	if (start_node == 's' || end_node == 't')
	{
		if (start_node == 's')
			arc[0][end_node - 'A' + 1].max_stream = max_stream;
		if (end_node == 't')
			arc[start_node - 'A' + 1][max_node - 1].max_stream = max_stream;
	}
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].max_stream = max_stream;
}

void input_switch_initialize_flag(char start_node, char end_node, bool initialize_flag)
{
	if (start_node == 's' || end_node == 't')
	{
		if (start_node == 's')
			arc[0][end_node - 'A' + 1].initialize_flag = initialize_flag;
		if (end_node == 't')
			arc[start_node - 'A' + 1][max_node - 1].initialize_flag = initialize_flag;
	}
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].initialize_flag = initialize_flag;
}

void edge_initialize(bool state)
{
	char start_node = 0, end_node = 0;
	double max_stream = 0, available_stream = 0;
	bool initialize_flag = 1, correct_flag = 1;
	cout << "数组初始化开始......" << endl;
	cout << "请按照提示输入对应数据......" << endl;
	cout << "注意：若要终止数组初始化，在"始发节点"处输入字符'0'即可。" << endl;
	cout << "注意：网络图起始点用's',终止点用't'。" << endl;
	cout << "注意：若输入错误，只需将弧容量赋值为0，并重新输入该条一步通路即可。" << endl;
	while (1)
	{
		cout << "请输入始发节点(大写字母):"; cin >> start_node;
		if (start_node == '0'){cout << "输入结束!" << endl; break;}
		cout << "请输入终到节点(大写字母):"; cin >> end_node;
		cout << "请输入弧容量:"; cin >> max_stream;
		correct_flag = 1;//不然第一次输入错了，第二次输入correct_flag还是0，没法录值
		if (max_stream == 0)correct_flag = 0;
		if (state == 1)
		{
			cout << "请输入当前弧流量:"; cin >> available_stream;
			if(correct_flag)
				input_switch_available_stream(start_node, end_node, available_stream);
		}
		if (correct_flag)
		{
			input_switch_max_stream(start_node, end_node, max_stream);
			input_switch_initialize_flag(start_node, end_node, initialize_flag);
		}
	}
	//未被认为赋值的，initialize_flag = 0，弧容量无穷大；
	for (int i = 0; i < max_node; i++)
		for (int j = 0; j < max_node; j++)
			if (arc[i][j].initialize_flag == 0)
				arc[i][j].max_stream = INF;
}

为了表达简洁，可以引入宏定义的函数：

cpp 复制代码 
#define INPUT_SWITCH(name1,name2)\
	{if(start_node == 's' || end_node == 't')\
	{if(start_node == 's')arc[0][end_node - 'A' + 1].name1 = name2;\
	if(end_node == 't')arc[start_node - 'A' + 1][max_node - 1].name1 = name2;}\
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].name1 = name2;}

这样，只需要输入"name1"和"name2"，其中name1代表将要被赋值的二维结构体数组元素的某个成员变量（名），name2代表存储用户输入的、要赋值给该成员的变量（名），即可实现代码简化。

因为name1是结构体成员名，name2是局部变量名，所以两个变量作用域不同，互不干扰，可以都用同一个名字，使代码更为简化：

cpp 复制代码 
#define INPUT_SWITCH(name)\
	{if(start_node == 's' || end_node == 't')\
	{if(start_node == 's')arc[0][end_node - 'A' + 1].name = name;\
	if(end_node == 't')arc[start_node - 'A' + 1][max_node - 1].name = name;}\
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].name = name;}
cpp 复制代码 
void edge_initialize(bool state)
{
	char start_node = 0, end_node = 0;
	double max_stream = 0, available_stream = 0;
	bool initialize_flag = 1, correct_flag = 1;
	cout << "数组初始化开始......" << endl;
	cout << "请按照提示输入对应数据......" << endl;
	cout << "注意：若要终止数组初始化，在"始发节点"处输入字符'0'即可。" << endl;
	cout << "注意：网络图起始点用's',终止点用't'。" << endl;
	cout << "注意：若输入错误，只需将弧容量赋值为0，并重新输入该条一步通路即可。" << endl;
	while (1)
	{
		cout << "请输入始发节点(大写字母):"; cin >> start_node;
		if (start_node == '0'){cout << "输入结束!" << endl; break;}
		cout << "请输入终到节点(大写字母):"; cin >> end_node;
		cout << "请输入弧容量:"; cin >> max_stream;
		correct_flag = 1;//不然第一次输入错了，第二次输入correct_flag还是0，没法录值
		if (max_stream == 0)correct_flag = 0;
		if (state == 1)
		{
			cout << "请输入当前弧流量:"; cin >> available_stream;
			if(correct_flag)
				INPUT_SWITCH(available_stream);
		}
		if (correct_flag)
		{
			INPUT_SWITCH(max_stream);
			INPUT_SWITCH(initialize_flag);
		}
	}
	//未被认为赋值的，initialize_flag = 0，弧容量无穷大；
	for (int i = 0; i < max_node; i++)
		for (int j = 0; j < max_node; j++)
			if (arc[i][j].initialize_flag == 0)
				arc[i][j].max_stream = INF;
}

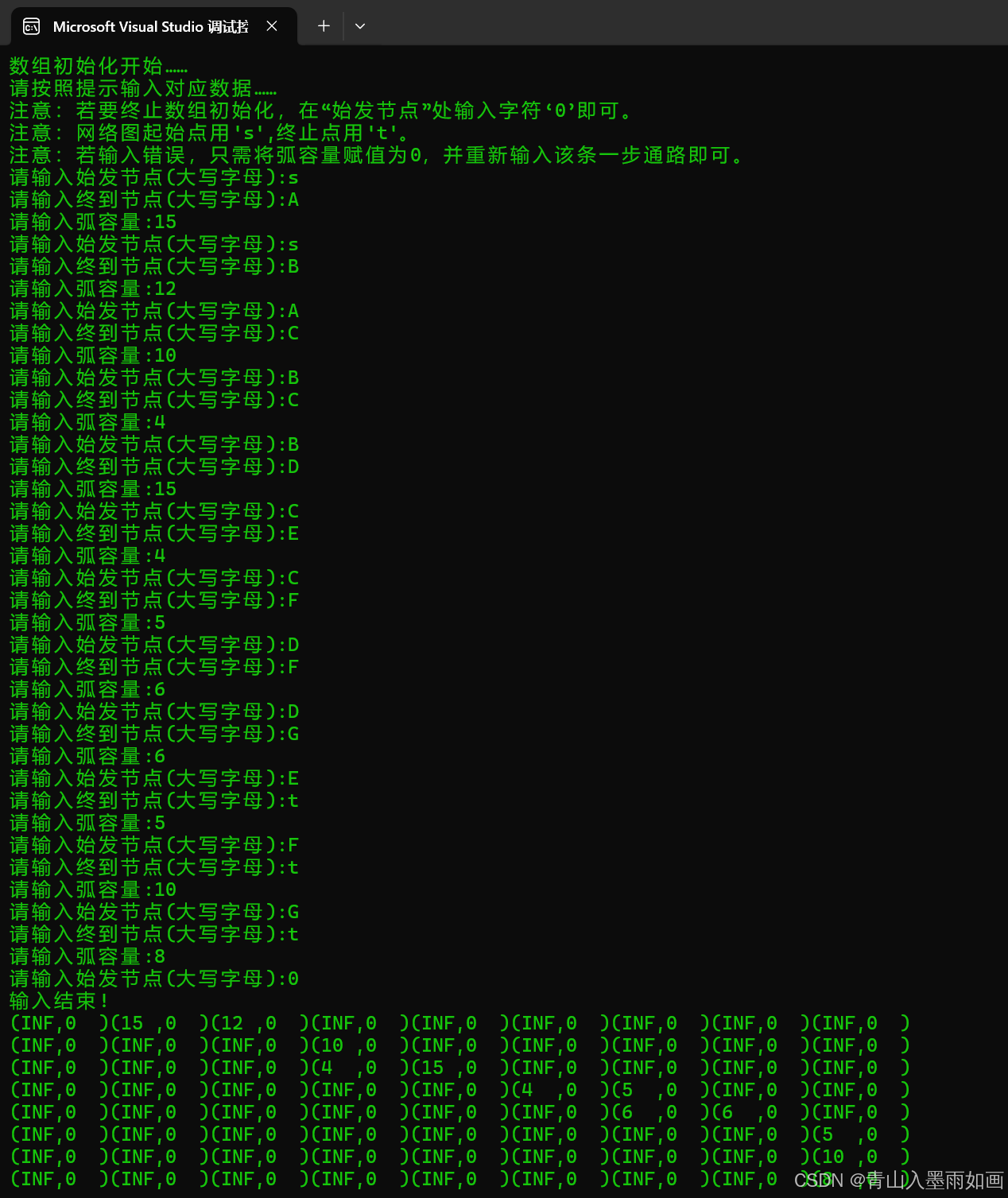
3.2.5、效果

结合结构体中对输出流的重定义和数组打印函数：

cpp 复制代码 
struct edge
{
	double max_stream;
	double available_stream;
	bool initialize_flag;
	bool calculation_flag;
	edge& operator = (edge& a)
	{
		if (this != &a)
		{
			calculation_flag = a.calculation_flag;
			initialize_flag = a.initialize_flag;
			max_stream = a.max_stream;
			available_stream = a.available_stream;
		}
		return *this;
	}
	friend ostream& operator <<(ostream& output, const node& a)
	{
		output << setiosflags(ios::left);
		output << "(";
		if (a.max_stream == INF)output << "INF";
		else output << setw(3) << a.max_stream;
		output << "," << setw(3) << a.available_stream << "),";
		return output;
	}
};

void edge_print()
{
	for (int i = 0; i < max_node; i++)
	{
		for (int j = 0; j < max_node; j++)
			cout << arc[i][j];
		cout << endl;
	}

}

则用户输入后可以打印该数组：

四、节点标号模块

4.1、综述

求解网络最大流问题，标号算法的视线途径是先找到增广链，之后修改增广链上的当前弧流量，直到无法找到增广链为止，当前网络可行流即为该网络的最大流。

寻找增广链的过程是一个【广搜】过程，BFS算法，那么很容易联想到【队列】；每次从队头弹出一个节点，都从队尾压入【可到达的】、【符合条件的】节点，为节点信息赋值标号；若队头节点是网络收点说明找到了增广链，否则没有增广链；

4.2、流程演示

（第一次搜索）

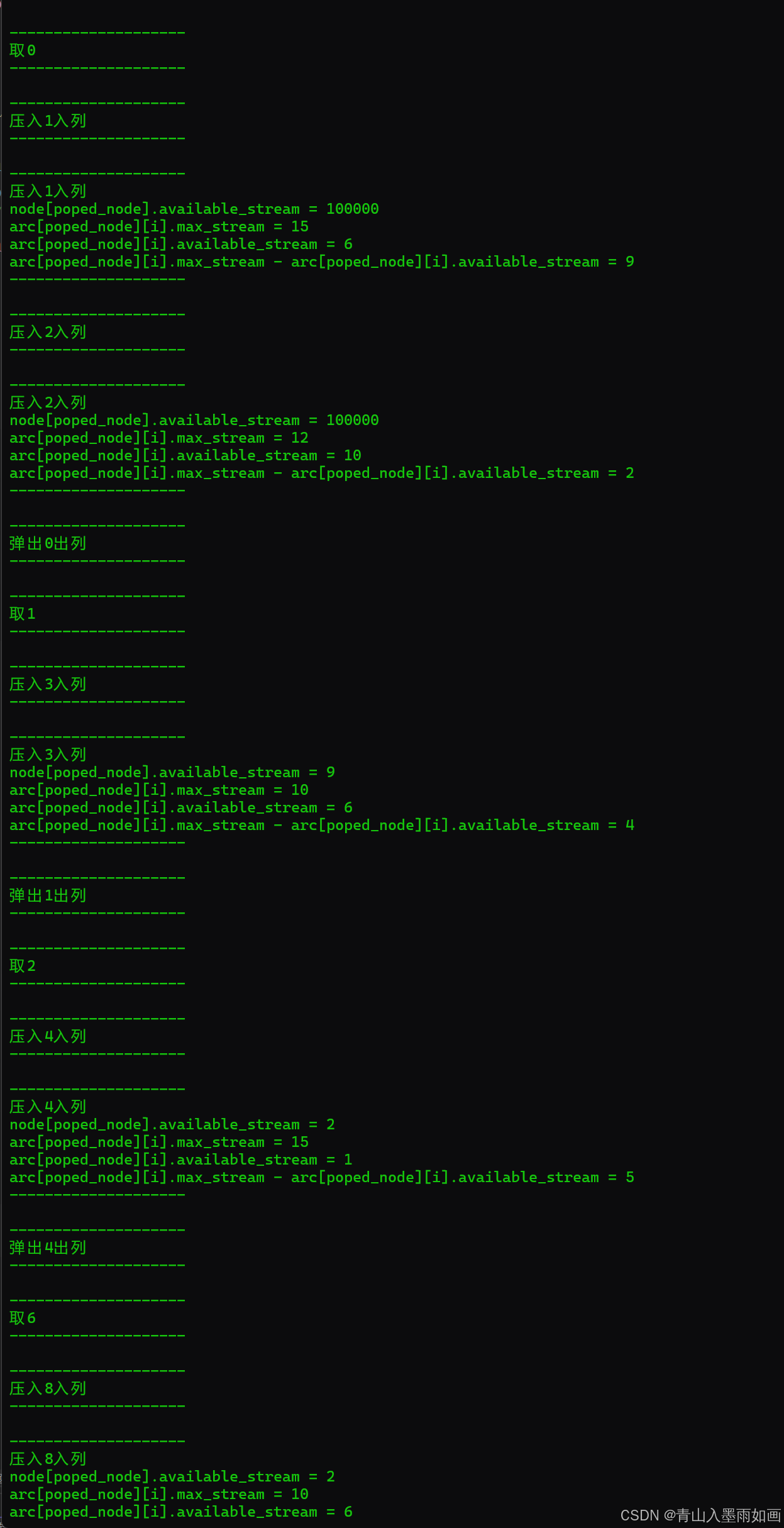
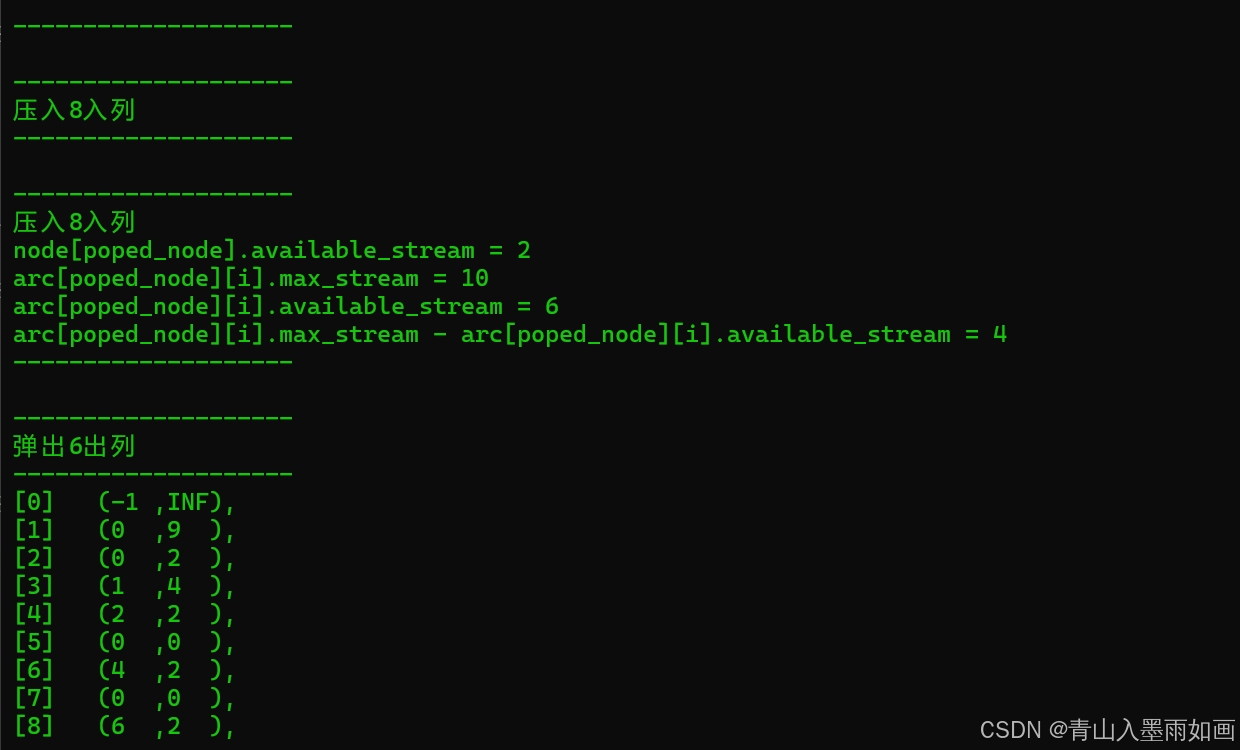
4.3、存储结构

因为标号算法是给【节点】标号，所以每个节点都要储存信息。可以定义结构体来【成员化】这些信息，并定义全局变量的一维结构体数组来存储【节点信息】。

根据综述和增广链实现过程中的分析，一个节点的节点信息需要有：

（1）检查标志checked_flag，如果这个节点所有【入度队列】和【出度队列】都检查完毕，则称这个节点被【检查过了】；在代码实现中，如果一个节点从队列头弹出，则该节点就已经被检查过了；

（2）标号标志selected_flag，如果这个节点已经【被标号】，那么这个节点就不能再被标号第二次；在代码实现中，如果一个节点已经入队，则该节点就已经被标号了；

（3）正向流标志positive_flag，因为增广链也考虑负向流，且正向流和负向流对【赋予节点的标号流量值】和【修改增广链】过程中操作过程完全不同，因此需要一个标记来标明这个标号节点相对于其源节点是正向的还是负向的；

（4）源节点source_node，因为要寻找增广链，所以标号时记录本节点的标号是从哪个节点【标过来的】，所以要记录一下；

（5）节点弧流量available_stream，能通过该节点的可行弧容量；为了修改增广链上所有弧的当前弧流量准备的。

cpp 复制代码 
struct label			    //节点的标号算法
{
	bool checked_flag;	    //检查标志
	bool selected_flag;	    //标号标志
	//检查了的一定标号了，但标号了的不一定检查好了
	bool positive_flag;     //正向弧还是反向弧
	int source_node;        //源节点是谁
	double available_stream;//容许增加的最大流量

	label& operator = (label& a)
	{
		if (this != &a)
		{
			checked_flag = a.checked_flag;
			selected_flag = a.selected_flag;
			positive_flag = a.positive_flag;
			source_node = a.source_node;
			available_stream = a.available_stream;
		}
		return *this;
	}

	friend ostream& operator <<(ostream& output, const label& a)
	{
		output << setiosflags(ios::left);
		output << "(" << setw(3) << a.source_node << ",";
		if (a.available_stream != INF)output << setw(3) << a.available_stream;
		else output << "INF";
		output << ")," << endl;
		return output;
	}
};

4.4、打印节点信息

cpp 复制代码 
struct label			    //节点的标号算法
{
	bool checked_flag;	    //检查标志
	bool selected_flag;	    //标号标志
	//检查了的一定标号了，但标号了的不一定检查好了
	bool positive_flag;     //正向弧还是反向弧
	int source_node;        //源节点是谁
	double available_stream;//容许增加的最大流量

	label& operator = (label& a)
	{
		if (this != &a)
		{
			checked_flag = a.checked_flag;
			selected_flag = a.selected_flag;
			positive_flag = a.positive_flag;
			source_node = a.source_node;
			available_stream = a.available_stream;
		}
		return *this;
	}

	friend ostream& operator <<(ostream& output, const label& a)
	{
		output << setiosflags(ios::left);
		output << "(" << setw(3) << a.source_node << ",";
		if (a.available_stream != INF)output << setw(3) << a.available_stream;
		else output << "INF";
		output << ")," << endl;
		return output;
	}
};

void print_label()
{
	for (int i = 0; i < max_node; i++)
		cout << "[" << i << "]   " << node[i];
}

4.5、节点信息初始化

cpp 复制代码 
struct label			    //节点的标号算法
{
	bool checked_flag;	    //检查标志
	bool selected_flag;	    //标号标志
	//检查了的一定标号了，但标号了的不一定检查好了
	bool positive_flag;     //正向弧还是反向弧
	int source_node;        //源节点是谁
	double available_stream;//容许增加的最大流量

	label& operator = (label& a)
	{
		if (this != &a)
		{
			checked_flag = a.checked_flag;
			selected_flag = a.selected_flag;
			positive_flag = a.positive_flag;
			source_node = a.source_node;
			available_stream = a.available_stream;
		}
		return *this;
	}

	friend ostream& operator <<(ostream& output, const label& a)
	{
		output << setiosflags(ios::left);
		output << "(" << setw(3) << a.source_node << ",";
		if (a.available_stream != INF)output << setw(3) << a.available_stream;
		else output << "INF";
		output << ")," << endl;
		return output;
	}
};

label node[max_node];
label initial_node;

void clean_label()
{
	for (int i = 0; i < max_node; i++)
		node[i] = initial_node;
}

4.6、标号模块

给所有节点标号的过程是从网络的发点开始广搜（BFS）的过程，结合流程中【step1：广度搜索算法寻找增广链】，其实就是对队列的【吞吐操作】。

step1：网络发点的处理

先将【网络发点】压入队列，并将网络发点node[0]的所有的特征进行赋值；

cpp 复制代码 
queue<int>q;
q.push(0);
node[0].checked_flag = 1;		//起始节点被检查
node[0].selected_flag = 1;		//起始节点被选中
node[0].positive_flag = 1;		//起始节点是正向的
node[0].source_node = -1;		//起始节点没有源节点
node[0].available_stream = INF;	//起始节点的可行流无穷大

定义一个局部变量，用于记录每次从队列头弹出的节点；

cpp 复制代码 
int poped_node = 0;

step2：选取入队节点的条件

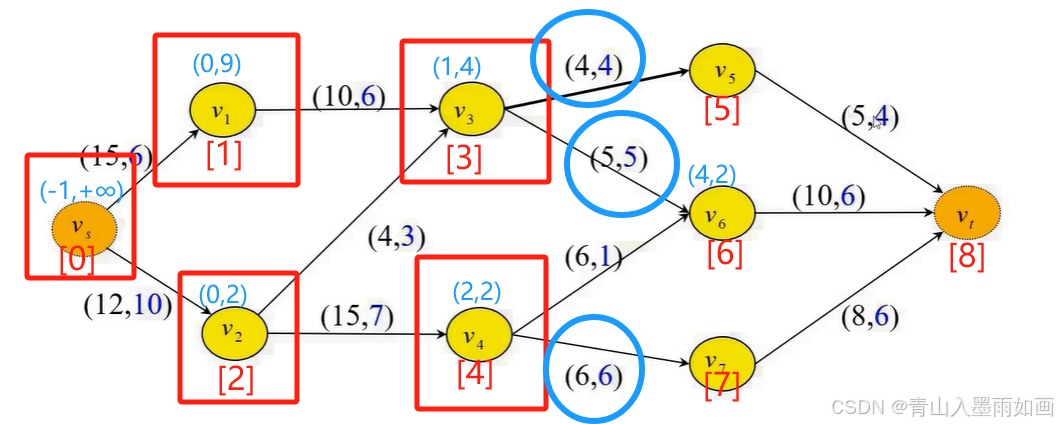
当队列非空时，每次从队列头取【注意不是取出】一个节点poped_node，将从poped_node出发【可以到达的】、【符合条件的】节点passable_node压入队列，其中：

【可以到达的节点】：从poped_node到passable_node有正向通路，或者从passable_node到poped_node有正向通路的节点，即（正向弧最大流≠INF） || （反向弧最大流≠INF）；

【符合条件的节点】：（没有被检查过的）&&（没有入过队的，即没被标号过的）&&（（正向弧最大流＞正向弧可行流的）||（负向弧最大流＞负向弧可行流的））

【注意】：弧最大流 = 弧可行流 的情况，该弧无法流入或流出，因此该点也不能入队，比如问题中的【V3->V5】、【V3->V6】、【V4->V7】:

step3： 最大增加流量的分类赋值

（1）若压入的passable_node对于poped_node是正向弧的话，应比较【弧可增加流量空间】和【poped_node节点最大可增加流量】的大小；

将【passable_node节点最大可增加流量】赋值为上述两者中较小的值；

将passable_node其他特征赋值：已标号未检查，正向弧，源节点；

cpp 复制代码 
for (int i = 0; i < max_node; i++)
	//对点的选择：只要没标号就行
	//对边的选择：本点到该点有通路||该点到本点有通路
{
	if(!node[i].selected_flag)//如果节点i未被标号
	{
		if ((arc[poped_node][i].max_stream != INF) &&
			(arc[poped_node][i].max_stream > 
            arc[poped_node][i].available_stream))
			//如果本点到该点正向弧有通路
		{
			q.push(i);//将该点压入队列
			//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
			node[i].selected_flag = 1;
			node[i].checked_flag = 0;
			node[i].positive_flag = 1;
			node[i].source_node = poped_node;
			node[i].available_stream =
				(node[poped_node].available_stream <
				(arc[poped_node][i].max_stream - 
                arc[poped_node][i].available_stream)
	            ) ? node[poped_node].available_stream :
				arc[poped_node][i].max_stream - 
                arc[poped_node][i].available_stream;
		}
        //else if......
}

（2）若压入的passable_node对于poped_node是反向弧的话，应比较【弧当前流量】和【poped_node节点最大可增加流量】的大小；

将【passable_node节点最大可增加流量】赋值为上述两者中较小的值；

将passable_node其他特征赋值：已标号未检查，反向弧，源节点；

cpp 复制代码 
for (int i = 0; i < max_node; i++)
	//对点的选择：只要没标号就行
	//对边的选择：本点到该点有通路||该点到本点有通路
{
	if(!node[i].selected_flag)//如果节点i未被标号
	{
		//if ......
		else if ((arc[i][poped_node].max_stream != INF) &&
			(arc[i][poped_node].max_stream > arc[i][poped_node].available_stream))
		{
			q.push(i);
			//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
			node[i].selected_flag = 1;
			node[i].checked_flag = 0;
			node[i].positive_flag = 0;
			node[i].source_node = poped_node;
			node[i].available_stream = node[poped_node].available_stream <
				arc[i][poped_node].available_stream ?
				node[poped_node].available_stream :
				arc[i][poped_node].available_stream;

		}
	}
}

分情况讨论的整体代码：

cpp 复制代码 
for (int i = 0; i < max_node; i++)
	//对点的选择：只要没标号就行
	//对边的选择：本点到该点有通路||该点到本点有通路
{
	if(!node[i].selected_flag)//如果节点i未被标号
	{
		if ((arc[poped_node][i].max_stream != INF) &&
			(arc[poped_node][i].max_stream > arc[poped_node][i].available_stream))
			//如果本点到该点正向弧有通路
		{
			q.push(i);//将该点压入队列
			//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
			node[i].selected_flag = 1;
			node[i].checked_flag = 0;
			node[i].positive_flag = 1;
			node[i].source_node = poped_node;
			node[i].available_stream =
				(node[poped_node].available_stream <
					(arc[poped_node][i].max_stream - arc[poped_node][i].available_stream)
					) ? node[poped_node].available_stream :
				arc[poped_node][i].max_stream - arc[poped_node][i].available_stream;

		}
		else if ((arc[i][poped_node].max_stream != INF) &&
			(arc[i][poped_node].max_stream > arc[i][poped_node].available_stream))
		{
			q.push(i);
			//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
			node[i].selected_flag = 1;
			node[i].checked_flag = 0;
			node[i].positive_flag = 0;
			node[i].source_node = poped_node;
			node[i].available_stream = node[poped_node].available_stream <
				arc[i][poped_node].available_stream ?
				node[poped_node].available_stream :
				arc[i][poped_node].available_stream;

		}
	}
}

step4：弹出队列节点的处理

弹出队列头的节点poped_node

给该节点标为已经检查过的节点；

cpp 复制代码 
q.pop();
node[poped_node].checked_flag = 1;

step5：标号结束后判断是否存在增广链

【增广链存在的根本标志】是队列压入了【网络的收点】。当poped_node ==收点时，标号过程找到了一条增广链，否则没有找到增广链；

所以可以定义一个bool类型的变量用来记录是否找到了增广链初值设置为false；只有当poped_node == 收点时，该修改变量的赋值为true；函数结束后返回该变量，就可以在标号过程的同时获得是否找到了增广链的信息。

标号过程完整代码

cpp 复制代码 
//标号
bool node_label()
{
	queue<int>q;
	q.push(0);
	node[0].checked_flag = 1;		//起始节点被检查
	node[0].selected_flag = 1;		//起始节点被选中
	node[0].positive_flag = 1;		//起始节点是正向的
	node[0].source_node = -1;		//起始节点没有源节点
	node[0].available_stream = INF;	//起始节点的可行流无穷大

	int poped_node = 0;				//记录从队头取出来的节点
	
	bool exists_broaden_line = 0;	//记录网络是否找到了增广链

	while (!q.empty())
	{
		poped_node = q.front();						//取队头元素
		node[poped_node].selected_flag = 1;			//队头元素被标号
		if (poped_node == max_node - 1)				//如果队头元素是网络收点
		{exists_broaden_line = 1; q.pop(); break;}	//说明找到了增广链,
													//弹出队头并结束while循环
		//PRINT_LINES; cout << "取" << poped_node; PRINT_LINES;
		for (int i = 0; i < max_node; i++)
			//对点的选择：只要没标号就行
			//对边的选择：本点到该点有通路||该点到本点有通路
		{
			if(!node[i].selected_flag)//如果节点i未被标号
			{
				if ((arc[poped_node][i].max_stream != INF) &&
					(arc[poped_node][i].max_stream > arc[poped_node][i].available_stream))
					//如果本点到该点正向弧有通路
				{
					q.push(i);//将该点压入队列
					//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
					node[i].selected_flag = 1;			//节点已标号
					node[i].checked_flag = 0;			//节点未检查
					node[i].positive_flag = 1;			//正向弧
					node[i].source_node = poped_node;	//源节点是poped_node
					node[i].available_stream =
						(node[poped_node].available_stream <
							(arc[poped_node][i].max_stream - arc[poped_node][i].available_stream)
							) ? node[poped_node].available_stream :
						arc[poped_node][i].max_stream - arc[poped_node][i].available_stream;
				}
				else if ((arc[i][poped_node].max_stream != INF) &&
					(arc[i][poped_node].max_stream > arc[i][poped_node].available_stream))
				{
					q.push(i);
					//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
					node[i].selected_flag = 1;			//节点已标号
					node[i].checked_flag = 0;			//节点未检查
					node[i].positive_flag = 0;			//反向弧
					node[i].source_node = poped_node;	//源节点是poped_node
					node[i].available_stream = node[poped_node].available_stream <
						arc[i][poped_node].available_stream ?
						node[poped_node].available_stream :
						arc[i][poped_node].available_stream;
				}
			}
		}
		q.pop();							//弹出队头
		node[poped_node].checked_flag = 1;	//队头元素已检查
	}
	return exists_broaden_line;				//返回是否找到了增广链
}

五、调整模块

调整模块运行的前提是网络存在增广链。

调整模块运行的原理是从网络收点根据其源节点依次溯回，直至溯回到网络发点。

定义弧终点end_node = 网络收点，定义增广链最大增流add_stream为网络收点最大可增流；

建立死循环，终止条件是溯回到了网络发点，在循环内：

如果是正向弧，则将当前弧流量增加add_stream；如果是反向弧，则将当前弧流量减少add_stream；

循环结束后，格式化所有节点；

cpp 复制代码 
void adjust()
{
	int end_node = max_node - 1, start_node = 0;
	double add_stream = node[max_node - 1].available_stream;
	//cout << add_stream; return;
	while (1)
	{
		start_node = node[end_node].source_node;
		if (start_node == -1)break;
		//PRINT_LINES; cout << "start_node = " << start_node; PRINT_LINES;
		if (node[end_node].positive_flag == 1)
			arc[start_node][end_node].available_stream += add_stream;
		else if (node[end_node].positive_flag == 0)
			arc[start_node][end_node].available_stream -= add_stream;
		end_node = start_node;
	}
	clean_label();
}

六、最大流标号算法模块

前两个模块的综合。

cpp 复制代码 
double max_stream_labeling_algorithm()
{
	while (node_label())
		adjust();
	double feasiable_stream = 0;
	for (int i = 0; i < max_node; i++)
		if (arc[0][i].max_stream != INF)
			feasiable_stream += arc[0][i].available_stream;
	PRINT_LINES;
	cout << "网络最大流为:" << feasiable_stream;
	PRINT_LINES;
	return feasiable_stream;
}

七、整体代码

7.1、head.h【头文件】

cpp 复制代码 
#pragma once
#ifndef _HEAD__H
#define _HEAD__H
#include <iostream>
#include <iomanip>
#include <queue>
#include <stack>

inline const int max_node = 9;
inline const double INF = 1e5;

using namespace std;

#endif

7.2、edge.h【弧参量定义模块.h】

cpp 复制代码 
#pragma once
#ifndef _EDGE__H
#define _EDGE__H
#include "head.h"

#define INPUT_SWITCH(name)\
	{if(start_node == 's' || end_node == 't')\
	{if(start_node == 's')arc[0][end_node - 'A' + 1].name = name;\
	if(end_node == 't')arc[start_node - 'A' + 1][max_node - 1].name = name;}\
	else arc[start_node - 'A' + 1][end_node - 'A' + 1].name = name;}
//省事儿，不然需要传参name1,name2;.name1 = name2，太麻烦了,
//直接都叫一个名得了

struct edge
{
	double max_stream;
	double available_stream;
	bool initialize_flag;
	edge& operator = (edge& a)
	{
		if (this != &a)
		{
			initialize_flag = a.initialize_flag;
			max_stream = a.max_stream;
			available_stream = a.available_stream;
		}
		return *this;
	}
	friend ostream& operator <<(ostream& output, const edge& a)
	{
		output << setiosflags(ios::left);
		output << "{";
		if (a.max_stream == INF)output << "INF";
		else output << setw(3) << a.max_stream;
		output << "," << setw(3) << a.available_stream << "},";
		return output;
	}
};
inline edge arc[max_node][max_node] =
{
	{{INF,0  },{15 ,6  },{12 ,10 },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{10 ,6  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{4  ,3  },{15 ,7  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{4  ,4  },{5  ,5  },{INF,0  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{6  ,1  },{6  ,6  },{INF,0  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{5  ,4  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{10 ,6  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{8  ,6  }},
	{{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  },{INF,0  }}
};

//inline edge arc[max_node][max_node];

void edge_initialize(bool state);
void edge_print();
bool self_check();
#endif

7.3、node.h【标号调整模块.h】

cpp 复制代码 
#pragma once
#ifndef _NODE__H
#define _NODE_H
#include "head.h"
#include "edge.h"
#define PRINT_LINES {std::cout<<std::endl;for(int i = 0; i < 20; i++ )std::cout<<"-"; std::cout<<std::endl;}
struct label			//节点的标号算法
{
	bool checked_flag;	//检查标志
	bool selected_flag;	//标号标志
	//检查了的一定标号了，但标号了的不一定检查好了
	bool positive_flag;
	int source_node;
	double available_stream;

	label& operator = (label& a)
	{
		if (this != &a)
		{
			checked_flag = a.checked_flag;
			selected_flag = a.selected_flag;
			positive_flag = a.positive_flag;
			source_node = a.source_node;
			available_stream = a.available_stream;
		}
		return *this;
	}

	friend ostream& operator <<(ostream& output, const label& a)
	{
		output << setiosflags(ios::left);
		output << "(" << setw(3) << a.source_node << ",";
		if (a.available_stream != INF)output << setw(3) << a.available_stream;
		else output << "INF";
		output << ")," << endl;
		return output;
	}
};

inline label node[max_node];
inline label initial_node;

bool node_label();
void clean_label();
void print_label();

void adjust();
double max_stream_labeling_algorithm();
#endif // !_NODE__H

7.4、edge.cpp【弧参量定义模块.cpp】

cpp 复制代码 
#include "edge.h"

void edge_initialize(bool state)
{
	char start_node = 0, end_node = 0;
	double max_stream = 0, available_stream = 0;
	bool initialize_flag = 1, correct_flag = 1;
	cout << "数组初始化开始......" << endl;
	cout << "请按照提示输入对应数据......" << endl;
	cout << "注意：若要终止数组初始化，在"始发节点"处输入字符'0'即可。" << endl;
	cout << "注意：网络图起始点用's',终止点用't'。" << endl;
	cout << "注意：若输入错误，只需将弧容量赋值为0，并重新输入该条一步通路即可。" << endl;
	while (1)
	{
		cout << "请输入始发节点(大写字母):"; cin >> start_node;
		if (start_node == '0') { cout << "输入结束!" << endl; break; }
		cout << "请输入终到节点(大写字母):"; cin >> end_node;
		cout << "请输入弧容量:"; cin >> max_stream;
		correct_flag = 1;//不然第一次输入错了，第二次输入correct_flag还是0，没法录值
		if (max_stream == 0)correct_flag = 0;
		if (state == 1)
		{
			cout << "请输入当前弧流量:"; cin >> available_stream;
			if (correct_flag)
				INPUT_SWITCH(available_stream);
		}
		if (correct_flag)
		{
			INPUT_SWITCH(max_stream);
			INPUT_SWITCH(initialize_flag);
		}
	}
	//未被认为赋值的，initialize_flag = 0，弧容量无穷大；
	for (int i = 0; i < max_node; i++)
		for (int j = 0; j < max_node; j++)
			if (arc[i][j].initialize_flag == 0)
				arc[i][j].max_stream = INF;
}

void edge_print()
{
	for (int i = 0; i < max_node; i++)
	{
		for (int j = 0; j < max_node; j++)
			cout << arc[i][j];
		cout << endl;
	}

}

bool self_check()
{
	bool result_flag = 1;
	double total_in = 0, total_out = 0;
	for (int i = 0; i < max_node; i++)
	{
		total_in = 0, total_out = 0;
		for (int j = 0; j < max_node; j++)
		{
			if (arc[i][j].max_stream != INF)total_out += arc[i][j].max_stream;
			if (arc[j][i].max_stream != INF)total_in += arc[j][i].max_stream;
		}
		if (total_out != total_in)result_flag = 0;
	}
	return result_flag;
}

7.5、node.cpp【标号调整模块.cpp】

cpp 复制代码 
#include"node.h"

//标号
bool node_label()
{
	queue<int>q;
	q.push(0);
	node[0].checked_flag = 1;		//起始节点被检查
	node[0].selected_flag = 1;		//起始节点被选中
	node[0].positive_flag = 1;		//起始节点是正向的
	node[0].source_node = -1;		//起始节点没有源节点
	node[0].available_stream = INF;	//起始节点的可行流无穷大

	int poped_node = 0;				//记录从队头取出来的节点
	
	bool exists_broaden_line = 0;	//记录网络是否找到了增广链

	while (!q.empty())
	{
		poped_node = q.front();						//取队头元素
		node[poped_node].selected_flag = 1;			//队头元素被标号
		if (poped_node == max_node - 1)				//如果队头元素是网络收点
		{exists_broaden_line = 1; q.pop(); break;}	//说明找到了增广链,
													//弹出队头并结束while循环
		//PRINT_LINES; cout << "取" << poped_node; PRINT_LINES;
		for (int i = 0; i < max_node; i++)
			//对点的选择：只要没标号就行
			//对边的选择：本点到该点有通路||该点到本点有通路
		{
			if(!node[i].selected_flag)//如果节点i未被标号
			{
				if ((arc[poped_node][i].max_stream != INF) &&
					(arc[poped_node][i].max_stream > arc[poped_node][i].available_stream))
					//如果本点到该点正向弧有通路
				{
					q.push(i);//将该点压入队列
					//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
					node[i].selected_flag = 1;			//节点已标号
					node[i].checked_flag = 0;			//节点未检查
					node[i].positive_flag = 1;			//正向弧
					node[i].source_node = poped_node;	//源节点是poped_node
					node[i].available_stream =
						(node[poped_node].available_stream <
							(arc[poped_node][i].max_stream - arc[poped_node][i].available_stream)
							) ? node[poped_node].available_stream :
						arc[poped_node][i].max_stream - arc[poped_node][i].available_stream;
					//PRINT_LINES;
					//cout << "压入" << i << "入列" << endl;
					//cout << "node[poped_node].available_stream = " << node[poped_node].available_stream << endl;
					//cout << "arc[poped_node][i].max_stream = " << arc[poped_node][i].max_stream << endl;
					//cout << "arc[poped_node][i].available_stream = " << arc[poped_node][i].available_stream << endl;
					//cout << "arc[poped_node][i].max_stream - arc[poped_node][i].available_stream = " <<
					//	arc[poped_node][i].max_stream - arc[poped_node][i].available_stream;
					//PRINT_LINES;
				}
				else if ((arc[i][poped_node].max_stream != INF) &&
					(arc[i][poped_node].max_stream > arc[i][poped_node].available_stream))
				{
					q.push(i);
					//PRINT_LINES; cout << "压入" << i << "入列"; PRINT_LINES;
					node[i].selected_flag = 1;			//节点已标号
					node[i].checked_flag = 0;			//节点未检查
					node[i].positive_flag = 0;			//反向弧
					node[i].source_node = poped_node;	//源节点是poped_node
					node[i].available_stream = node[poped_node].available_stream <
						arc[i][poped_node].available_stream ?
						node[poped_node].available_stream :
						arc[i][poped_node].available_stream;
					//PRINT_LINES;
					//cout << "压入" << i << "入列" << endl;
					//cout << "node[poped_node].available_stream = " << node[poped_node].available_stream << endl;
					//cout << "arc[i][poped_node].available_stream = " << arc[i][poped_node].available_stream;
					//PRINT_LINES;
				}
			}
		}
		q.pop();							//弹出队头
		//PRINT_LINES; cout << "弹出" << poped_node << "出列"; PRINT_LINES;
		node[poped_node].checked_flag = 1;	//队头元素已检查
	}
	return exists_broaden_line;				//返回是否找到了增广链
}

void clean_label()
{
	for (int i = 0; i < max_node; i++)
		node[i] = initial_node;
}

void print_label()
{
	for (int i = 0; i < max_node; i++)
		cout << "[" << i << "]   " << node[i];
}

void adjust()
{
	int end_node = max_node - 1, start_node = 0;
	double add_stream = node[max_node - 1].available_stream;
	//cout << add_stream; return;
	while (1)
	{
		start_node = node[end_node].source_node;
		if (start_node == -1)break;
		//PRINT_LINES; cout << "start_node = " << start_node; PRINT_LINES;
		if (node[end_node].positive_flag == 1)
			arc[start_node][end_node].available_stream += add_stream;
		else if (node[end_node].positive_flag == 0)
			arc[start_node][end_node].available_stream -= add_stream;
		end_node = start_node;
	}
	clean_label();
}

double max_stream_labeling_algorithm()
{
	while (node_label())
		adjust();
	double feasiable_stream = 0;
	for (int i = 0; i < max_node; i++)
		if (arc[0][i].max_stream != INF)
			feasiable_stream += arc[0][i].available_stream;
	PRINT_LINES;
	cout << "网络最大流为:" << feasiable_stream;
	PRINT_LINES;
	return feasiable_stream;
}

7.6、source.cpp【源文件】

cpp 复制代码 
#include"head.h"
#include"edge.h"
#include"node.h"

int main()
{
	system("color 0A");
	//edge_initialize(1);
	//edge_print();
	//cout << self_check();

	//node_label();
	//print_label();
	//cout << arc[0][1].max_stream << endl << arc[0][1].available_stream << endl;

	//node_label();
	//adjust();
	//print_label();
	//edge_print();

	max_stream_labeling_algorithm();
	return 0;
}

八、运行结果

答案正确。

相关推荐
chao1898442 小时前
基于MATLAB实现NSGA-II算法
开发语言·算法·matlab
星环处相逢2 小时前
Ansible-Playbook 剧本编写全攻略：从入门到进阶
linux·服务器·网络
mmz12072 小时前
差分数组（c++）
c++·算法
一岁天才饺子2 小时前
SSRF漏洞绕过与漏洞解决
网络·网络安全·ssrf
xu_yule2 小时前
算法基础-图论基础
数据结构·c++·算法·图论·dfs·bfs·最小生成树
月明长歌2 小时前
【码道初阶】LeetCode面试题 17.14 最小 K 个数：两种堆解法的“同题不同命”
算法·leetcode·职场和发展
AI即插即用2 小时前
即插即用系列 | CMPB PMFSNet：多尺度特征自注意力网络，打破轻量级医学图像分割的性能天花板
网络·图像处理·人工智能·深度学习·神经网络·计算机视觉·视觉检测
程芯带你刷C语言简单算法题2 小时前
Day33~实现一个算法来识别一个字符串。
c语言·算法·c
学编程就要猛2 小时前
算法：2.复写零
java·数据结构·算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05BongoCat - 跨平台键盘猫动画工具06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07jdk21下载、安装（Windows、Linux、macOS）08Labelme从安装到标注：零基础完整指南09CentOS的ISO镜像下载10Open-AutoGLM Windows 安装部署教程