（leetcode）力扣100 19螺旋矩阵（方向数组/边界把控）

题目

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

数据范围

java 复制代码

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

测试用例

示例1

java 复制代码

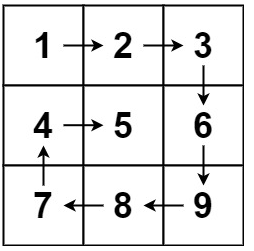
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例2

java 复制代码

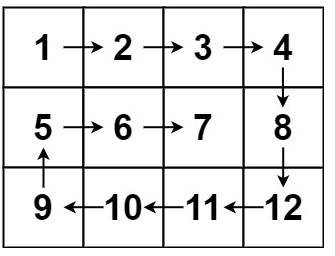
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

题解（博主思路，时间O（nm），空间O（1））

java 复制代码

class Solution {
    static int dire[][]={{0,1,0,-1},{1,0,-1,0}};
    static int direpos;
    public static List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res=new ArrayList<>();
        direpos=0;
        int m=matrix.length;
        int n=matrix[0].length;
        int tm=m;
        int tn=n;
        int x=-1;
        int y=0;
        int all=n*m;
        for(int i=0;i<all;i++){
            x=x+dire[1][direpos];
            y=y+dire[0][direpos];
            res.add(matrix[y][x]);
            if(direpos==0||direpos==2){
                tn--;
                if(tn==0){
                    direpos=(direpos+1)%4;
                    tn=n-1;
                    n=n-1;
                    tm--;
                }
            }else{
                tm--;
                if(tm==0){
                    direpos=(direpos+1)%4;
                    tm=m-1;
                    m=m-1;
                }
            }
        }
        return res;
    }
}

官解1（时间O（NM），空间O（NM））

java 复制代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        boolean[][] visited = new boolean[rows][columns];
        int total = rows * columns;
        int row = 0, column = 0;
        int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order.add(matrix[row][column]);
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
}

官解2（时间O(nm）,空间O(1))

java 复制代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

思路

这道题算是一道简单的题，因为他的思路很简单，做法无非两种，第一个官解方法一，通过预定方法来做，第二个方法无非就是通过几个变量来维护方向，也就是官解的第二种解法。思路都不难，这道题难度在细节处理，边界处理容易出问题。博主的方法采用了方向数组，但不想官解1使用了记忆数组来存储走过的路，而是通过（tn,tm）两个变量维护剩余步数，来达到节约空间的目的。

综上，其实官解的方法二还是更推荐一些的，虽然博主方法的空间复杂度同样是O（1），但博主的方法边界处理更麻烦。博主的思路是，横向移动时，横向的可移动距离-1，纵向的可移动距离也要-1，纵向移动到底时，只有纵向的可移动距离-1。然后维护每次定向移动的可移动距离即可。

说实话博主的方法和官方方法二思路其实大相径庭，一个是在每一次行动中维护边界，一个在运行一圈后总的维护边界，仁者见仁，智者见智吧。